2013-2014学年高中数学人教A版选修2-3同步辅导与检测:2.4正态分布
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-3同步辅导与检测:2.4正态分布 |  | |
| 格式 | zip | ||
| 文件大小 | 827.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 12:51:05 | ||
图片预览










文档简介
课件40张PPT。2.4 正 态 分 布随机变量及其分布通过实际问题,借助直观(如实际问题的直方图),认识正态分布曲线的特点及曲线所表示的意义.基础梳理1.如果函数为: μ,σ(x)= x∈(-∞,+∞),其中μ,σ(σ>0)为参数,称 μ,σ(x)的图象为正态分布密度曲线.简称________.如果随机变量X服从正态分布,则记作______________.
说明:(1)正态曲线由参数μ,σ唯一确定,μ,σ分别表示总体的平均数和标准差;即:Eξ=________,Dξ=______;正态曲线 X~N(μ,σ2)μσ2(2)其函数图象称为正态曲线.
例如:如果随机变量ξ的概率密度函数为: μ,σ(x)=
,x∈(-∞,+∞),则称ξ服从______________.此时μ=________,σ=________,记作______________.
2.一般地,如果对于任何实数a<b,随机变量X满足P(a<X≤b)=?μ,σ(x)dx,则称X的分布为__________.表示的意义:X是一个随机变量,X落在区间(a,b]的概率为P(a<X≤b).3.正态曲线(如右图)的特点:
(1)曲线在x轴上方,即:f(x)>0,与x轴不相交;
(2)曲线是单峰的,它关于直线x=μ对称;标准正态分布01ξ~N(0,1)正态分布(3)曲线当x=μ时达到最高点,f(x)有峰值(最大值);
(4)正态曲线下的总面积等于1,即
(5)若固定σ,随μ值的不同,曲线沿x轴平移,且形状不变;
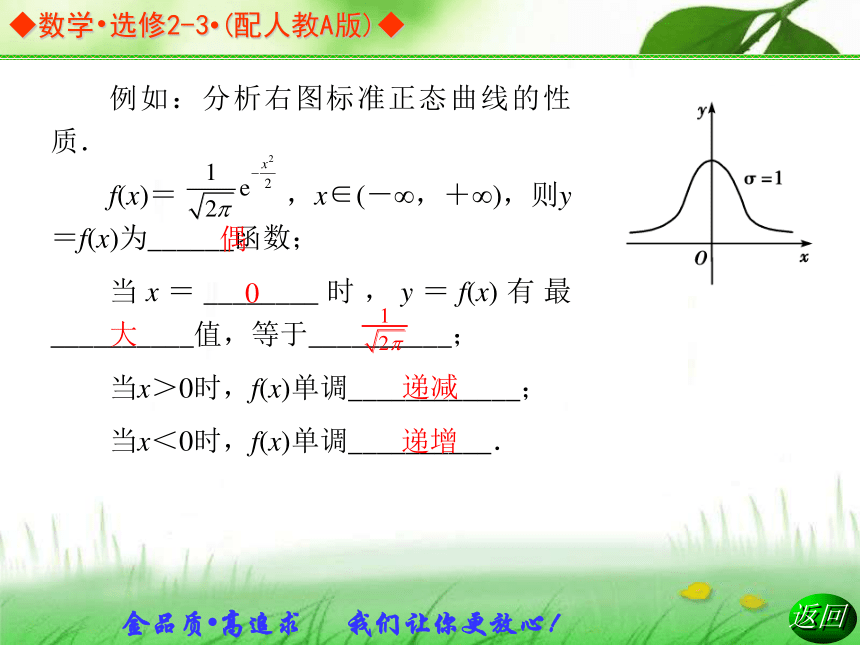
(6)若固定μ,当σ值增大时,曲线变得矮而胖,取远离μ值的机会相对较多,故分布越分散;当σ值减小时,曲线变得高瘦,取远离μ值的机会相对较少,故分布越集中.例如:分析右图标准正态曲线的性质.
f(x)= ,x∈(-∞,+∞),则y=f(x)为______函数;
当x=________时,y=f(x)有最__________值,等于__________;
当x>0时,f(x)单调____________;
当x<0时,f(x)单调__________.偶0大递减递增4.3σ原则:正态总体几乎取值于区间_______________之内,而在此区间以外取值的概率只有________,通常认为这种情况在一次试验中几乎不可能发生.例如:在某次大型考试中,某班同学的成绩服从正态分布N(80,25),现已知该班同学中成绩在75~85分的同学有34人,则该班约有________个人.(μ-3σ,μ+3σ)0.002650A.P(x)= ,μ,σ(σ>0)都是实数
B.P(x)=
C.P(x)=
D.P(x)=自测自评1.下列函数是标准正态密度函数的是( )B3.(2011年福建宁德联考)设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=( )
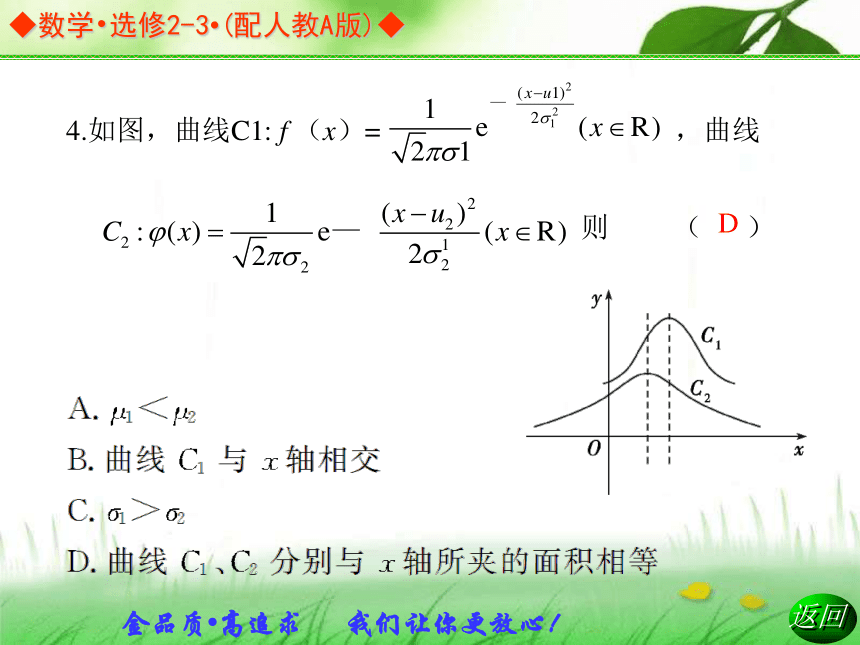
A. +p B.1-p C.1-2p D. -p2.设正态密度函数为P(x)= ,x∈R,则总体的均值为______,方差为________.14解析:由P(ξ>1)=p知P(-1<ξ<0)=1-2p,所以P(-1<ξ<0)= -p.答案:D4.如图,曲线C1: f (x)= ,曲线则 ( )D正态分布的相关概念 把一条正态曲线C1沿着横轴方向向右移动2个单位,得到新的一条曲线C2,下列说法中不正确的是( )
A.曲线C2仍然是正态曲线
B.曲线C1和曲线C2的最高点的纵坐标相等
C.以曲线C2为概率密度曲线的总体的期望比以曲线C1为概率的密度曲线的总体的期望大2
D.以曲线C2为概率的密度曲线的总体的方差比以曲线C1为概率的密度曲线的总体的方差大2解析:正态曲线沿着横轴方向水平移动只改变对称轴位置,曲线的形状没有改变,所得的曲线依然是正态曲线.
在正态曲线沿着横轴方向水平移动的过程中,σ始终保持不变,所以曲线的最高点的纵坐标(即正态密度函数的最大值 )不变,方差σ2也没有变化.设曲线C1的对称轴为x=μ,那么曲线C2的对称轴为x=μ+2,说明期望从μ变到了μ+2,增大了2.
答案:D跟踪练习1.关于正态曲线性质的叙述:
①曲线关于直线x=μ对称,在x轴上方;
②曲线关于直线x=σ对称,只有当x∈(-3σ,3σ)时才在x轴上方;
③曲线关于y轴对称,因为曲线对应的正态密度函数是一个偶函数;
④曲线在x=μ时,处于最高点,由这一点向左右两边延伸时,曲线逐渐降低;
⑤曲线的对称轴由μ确定,曲线的形状由σ确定;⑥σ越大,曲线越“矮胖”,σ越小,曲线越“高瘦”.
其中正确的是( )
A.①④⑤⑥ B.②④⑤
C.③④⑤⑥ D.①⑤⑥
答案:A正态曲线的方程及特征 如图所示是一个正态曲线.试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差.跟踪练习2.设随机变量ξN(μ,σ2),且P(ξ≤C)=P(ξ>C),则C等于( )
A.0 B.μ
C.-μ D.σB应用正态分布曲线求概率 在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为________.
分析:由ξ~N(1,σ2)可知,密度函数关于x=1对称,从而ξ在(0,1)内取值的概率就等于(1,2)内的概率.解析:由ξ~N(1,σ2),得ξ落在(0,1)及(1,2)内取值的概率相同,均为0.4,如下图所示,故ξ落在(0,2)内取值的概率为P(0< ξ<1)+P(1<ξ<2)=0.4+0.4=0.8.
答案:0.8点评:解答此类题目的关键在于充分利用正态曲线的对称性,把待求区间内的概率向已知区间内的概率进行转化.在此过程中充分体现数形结合及化归(转化)的数学思想.跟踪练习3.例3的条件不变,则P(ξ≥2)=________.0.1正态分布在实际问题中的应用 一台机床生产一种尺寸为10 mm的零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm):10.2,10.1,10,9.8,9.9,10.3,9.7,10,9.9,10.1.如果机床生产零件的尺寸η服从正态分布,求正态分布的概率密度函数式.解析:依题意得
μ= (10.2+10.1+10+9.8+9.9+10.3+9.7+10+ 9.9+10.1)=10.
σ2= [(10.2-10)2+(10.1-10)2+(10-10)2+(9.8-10)2+(9.9-10)2+(10.3-10)2+(9.7-10)2+(10-10)2+(9.9-10)2+(10.1-10)2]=0.03.即μ=10,σ2=0.03.
所以η的概率密度函数为φ(x)= . 跟踪练习4.某人从某城市的南郊乘公交车前往北区火车站,由于交通拥挤,所需时间(单位:分)服从X~N(50,102),求他在时间段(30,70)内赶到火车站的概率.解析:因为X~N(50,102),所以μ=50,σ=10.
所以P(30<X≤70)=P(50-2×10<X≤50+2×10)=0.954 4.
所以所求概率为0.954 4. 若一个正态分布的概率密度函数是一个偶函数,且该函数的最大值为 .
(1)求该正态分布的概率密度函数的表达式;
(2)求正态总体在(-4,4]上的概率.
分析:要确定一个正态分布的概率密度函数的表达式,关键是求表达式中的两个参数μ,σ的值,其中μ决定曲线的对称轴的位置,σ则与曲线的形状和最大值有关.解析:(1)由于该正态分布的概率密度函数是一个偶函数,所以其图象关于y轴对称,即μ=0.(2)P(-4<x≤4)=P(0-4<x≤0+4)
=P(μ-σ<X≤μ+σ)=0.683.
点评:解决此类问题的关键是正确理解函数表达式与正态曲线的关系,掌握函数表达式中参数的取值变化对曲线的影响.5.(2012年佛山模拟)已知随机变量X服从正态分布N(μ,σ2),且P(μ-2σ<X≤μ+2σ)=0.954 4,P(μ-σ <X≤μ+σ)=0.6 826,若μ=4,σ=1,则P(5<X<6)=( )
A.0.135 8 B.0.135 9 C.0.271 6 D.0.271 8跟踪练习1.若f(x)= ,x∈R,则下列判断中正确的是( )
A.有最大值,也有最小值 B.有最大值,无最小值
C.无最大值,有最小值 D.无最大值,也无最小值
2.正态总体N(0,1)中数值落在(-∞,-3)∪(3,+∞)的概率为( )
A.4.6% B.0.002
C.0.003 D.0.03%BC3.如右图所示是当ξ取三个不同值σ1,σ2,σ3,的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )
A.σ1>1>σ2>σ3>0
B.0<σ1<σ2<1<σ3
C.σ1>σ2>1>σ3>0
D.0<σ1<σ2=1<σ34.若随机变量满足正态分布N(μ,σ2),则关于正态曲线性质的叙述正确的是( )
A.σ越大,曲线越“矮胖”,σ越小,曲线越“高瘦”
B.σ越大,曲线越“高瘦”,σ越小,曲线越“矮胖”
C.σ的大小和曲线的“高瘦”、“矮胖”没有关系
D.曲线的“高瘦”、“矮胖”受到μ的影响DA5.已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,则P(-2≤ξ≤2)=( )
A.0.477 B.0.625 C.0.954 D.0.977解析:因为随机变量ξ服从正态分布N(0,σ2),所以正态曲线关于直线x=0对称,又P(ξ>2)=0.023,所以P(ξ<-2)=0.023,所以P(-2≤ξ≤2)=1-P(ξ>2)-P(ξ<-2)=1-2×0.023=0.954,故选C.
答案:C6.已知随机变量X服从正态分布N(2,σ2),P(X<4)=0.84,则P(X≤0)=( )
A.0.16 B.0.32 C.0.68 D.0.84A7.(2011年南开中学月考)已知随机变量ξ服从正态分布N(2,σ2)则P(ξ<2)=( )解析:由题意知平均值为2,因此P(ξ<2)= .答案:D8.已知正态总体的数据落在区间(-3,-1)里的概率和落在区间(3,5)里的概率相等,那么这个正态总体的数学期望为________.19.设X~N(0,1):
①P(-ε<X<0)=P(0<X<ε);
②P(X<0)=0.5;
③已知P(-1<X<1)=0.683,则P(X<-1)=0.158 5;
④若P(-2<X<2)=0.954,则P(X<2)=0.977;
⑤若P(-3<X<3)=0.997,则P(X<3)=0.998 5.
其中正确的有____________(填序号).①②③④⑤10.(1)已知随机变量X服从正态分布N(0,σ2),且P(-2≤X≤0)=0.4,则P(X>2)=________________.0.1(2)均值为2,标准差为 的正态分布的概率密度函数是_________________________.11.(1)随机变量X服从正态分布N(0,1),如果P(X<1)=0.841 3,求P(-1<X<0)的值;
(2)如图是正态分布N(0,1)的正态曲线图,已知P(X≤-a)=m,求图中阴影部分的面积.(3)如图所示,是一个正态曲线,试根据图象写出其正态分布密度曲线的解析式,并求出正态总体随机变量的均值和方差.解析:(1)解法一:由对称性可知
P(-1<X<0)=P(0<X<1),
而P(X<1)=0.8413,P(X≤0)=0.5,
∴P(-1<X<0)=P(X<1)-P(X≤0)=0.841 3-0.5=0.341 3.
解法二:∵P(X<1)=0.841 3,
∴P(X≥1)=P(X≤-1)=1-0.841 3=0.158 7.
P(-1<X<0)=P(0<X<1)= [1-P(X≥1)-P(X≤-
1)]= (1-2×0.158 7)=0.341 3.
(2)∵P(X≤-a)=m,由正态曲线的对称性可知:
P(X≥a)=m,从而P(-a<X<a)=1-P(X≤-a)-P(X≥a)=1-2m,
从而阴影部分的面积S= P(-a<X<a)= (1-2m)= -m.(3)从给出的正态曲线可知,该正态曲线关于直线x=20对称,最大值为 ,所以μ=20.?
由 ,解得 .?于是正态分布密度曲线的解析式是?
x∈(-∞,+∞).?
均值和方差分别是20和2.12.工厂制造的某机械零件尺寸X服从正态分布N ,问在一次正常的试验中,取1 000个零件时,不属于区间(3,5)这个尺寸范围内的零件大约多少个?
解析:不属于区间(3,5)的概率为
P(X≤3)+P(X≥5)=1-P(3<X<5)
=1-P(|X-4|<1).
因为X~N ,
所以μ=4,σ= .
所以1-P(|X-4|<1)=1-P(|X-μ|<3σ)=1-0.997=0.003.
1 000×0.003=3(个).1.求正态总体X取值小于x的概率
若X~N(μ,σ2),则P(X2.利用正态密度曲线的对称性解题
(1)若X~N(μ,σ2),则由正态密度曲线的对称性可知
①P(X>μ)=P(X≤μ)= ;
②P(μ-σ④P(μ-3σ<X≤μ)=P(μ(2)若X~N(0,1),则正态密度曲线关于y轴对称,于是
①P(X<x)+P(X<-x)=1;
②P(X<-x)=P(X>x).感谢您的使用,退出请按ESC键本小节结束
说明:(1)正态曲线由参数μ,σ唯一确定,μ,σ分别表示总体的平均数和标准差;即:Eξ=________,Dξ=______;正态曲线 X~N(μ,σ2)μσ2(2)其函数图象称为正态曲线.
例如:如果随机变量ξ的概率密度函数为: μ,σ(x)=
,x∈(-∞,+∞),则称ξ服从______________.此时μ=________,σ=________,记作______________.
2.一般地,如果对于任何实数a<b,随机变量X满足P(a<X≤b)=?μ,σ(x)dx,则称X的分布为__________.表示的意义:X是一个随机变量,X落在区间(a,b]的概率为P(a<X≤b).3.正态曲线(如右图)的特点:
(1)曲线在x轴上方,即:f(x)>0,与x轴不相交;
(2)曲线是单峰的,它关于直线x=μ对称;标准正态分布01ξ~N(0,1)正态分布(3)曲线当x=μ时达到最高点,f(x)有峰值(最大值);
(4)正态曲线下的总面积等于1,即
(5)若固定σ,随μ值的不同,曲线沿x轴平移,且形状不变;
(6)若固定μ,当σ值增大时,曲线变得矮而胖,取远离μ值的机会相对较多,故分布越分散;当σ值减小时,曲线变得高瘦,取远离μ值的机会相对较少,故分布越集中.例如:分析右图标准正态曲线的性质.
f(x)= ,x∈(-∞,+∞),则y=f(x)为______函数;
当x=________时,y=f(x)有最__________值,等于__________;
当x>0时,f(x)单调____________;
当x<0时,f(x)单调__________.偶0大递减递增4.3σ原则:正态总体几乎取值于区间_______________之内,而在此区间以外取值的概率只有________,通常认为这种情况在一次试验中几乎不可能发生.例如:在某次大型考试中,某班同学的成绩服从正态分布N(80,25),现已知该班同学中成绩在75~85分的同学有34人,则该班约有________个人.(μ-3σ,μ+3σ)0.002650A.P(x)= ,μ,σ(σ>0)都是实数
B.P(x)=
C.P(x)=
D.P(x)=自测自评1.下列函数是标准正态密度函数的是( )B3.(2011年福建宁德联考)设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=( )
A. +p B.1-p C.1-2p D. -p2.设正态密度函数为P(x)= ,x∈R,则总体的均值为______,方差为________.14解析:由P(ξ>1)=p知P(-1<ξ<0)=1-2p,所以P(-1<ξ<0)= -p.答案:D4.如图,曲线C1: f (x)= ,曲线则 ( )D正态分布的相关概念 把一条正态曲线C1沿着横轴方向向右移动2个单位,得到新的一条曲线C2,下列说法中不正确的是( )
A.曲线C2仍然是正态曲线
B.曲线C1和曲线C2的最高点的纵坐标相等
C.以曲线C2为概率密度曲线的总体的期望比以曲线C1为概率的密度曲线的总体的期望大2
D.以曲线C2为概率的密度曲线的总体的方差比以曲线C1为概率的密度曲线的总体的方差大2解析:正态曲线沿着横轴方向水平移动只改变对称轴位置,曲线的形状没有改变,所得的曲线依然是正态曲线.
在正态曲线沿着横轴方向水平移动的过程中,σ始终保持不变,所以曲线的最高点的纵坐标(即正态密度函数的最大值 )不变,方差σ2也没有变化.设曲线C1的对称轴为x=μ,那么曲线C2的对称轴为x=μ+2,说明期望从μ变到了μ+2,增大了2.
答案:D跟踪练习1.关于正态曲线性质的叙述:
①曲线关于直线x=μ对称,在x轴上方;
②曲线关于直线x=σ对称,只有当x∈(-3σ,3σ)时才在x轴上方;
③曲线关于y轴对称,因为曲线对应的正态密度函数是一个偶函数;
④曲线在x=μ时,处于最高点,由这一点向左右两边延伸时,曲线逐渐降低;
⑤曲线的对称轴由μ确定,曲线的形状由σ确定;⑥σ越大,曲线越“矮胖”,σ越小,曲线越“高瘦”.
其中正确的是( )
A.①④⑤⑥ B.②④⑤
C.③④⑤⑥ D.①⑤⑥
答案:A正态曲线的方程及特征 如图所示是一个正态曲线.试根据该图象写出其正态分布的概率密度函数的解析式,求出总体随机变量的期望和方差.跟踪练习2.设随机变量ξN(μ,σ2),且P(ξ≤C)=P(ξ>C),则C等于( )
A.0 B.μ
C.-μ D.σB应用正态分布曲线求概率 在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0).若ξ在(0,1)内取值的概率为0.4,则ξ在(0,2)内取值的概率为________.
分析:由ξ~N(1,σ2)可知,密度函数关于x=1对称,从而ξ在(0,1)内取值的概率就等于(1,2)内的概率.解析:由ξ~N(1,σ2),得ξ落在(0,1)及(1,2)内取值的概率相同,均为0.4,如下图所示,故ξ落在(0,2)内取值的概率为P(0< ξ<1)+P(1<ξ<2)=0.4+0.4=0.8.
答案:0.8点评:解答此类题目的关键在于充分利用正态曲线的对称性,把待求区间内的概率向已知区间内的概率进行转化.在此过程中充分体现数形结合及化归(转化)的数学思想.跟踪练习3.例3的条件不变,则P(ξ≥2)=________.0.1正态分布在实际问题中的应用 一台机床生产一种尺寸为10 mm的零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm):10.2,10.1,10,9.8,9.9,10.3,9.7,10,9.9,10.1.如果机床生产零件的尺寸η服从正态分布,求正态分布的概率密度函数式.解析:依题意得
μ= (10.2+10.1+10+9.8+9.9+10.3+9.7+10+ 9.9+10.1)=10.
σ2= [(10.2-10)2+(10.1-10)2+(10-10)2+(9.8-10)2+(9.9-10)2+(10.3-10)2+(9.7-10)2+(10-10)2+(9.9-10)2+(10.1-10)2]=0.03.即μ=10,σ2=0.03.
所以η的概率密度函数为φ(x)= . 跟踪练习4.某人从某城市的南郊乘公交车前往北区火车站,由于交通拥挤,所需时间(单位:分)服从X~N(50,102),求他在时间段(30,70)内赶到火车站的概率.解析:因为X~N(50,102),所以μ=50,σ=10.
所以P(30<X≤70)=P(50-2×10<X≤50+2×10)=0.954 4.
所以所求概率为0.954 4. 若一个正态分布的概率密度函数是一个偶函数,且该函数的最大值为 .
(1)求该正态分布的概率密度函数的表达式;
(2)求正态总体在(-4,4]上的概率.
分析:要确定一个正态分布的概率密度函数的表达式,关键是求表达式中的两个参数μ,σ的值,其中μ决定曲线的对称轴的位置,σ则与曲线的形状和最大值有关.解析:(1)由于该正态分布的概率密度函数是一个偶函数,所以其图象关于y轴对称,即μ=0.(2)P(-4<x≤4)=P(0-4<x≤0+4)
=P(μ-σ<X≤μ+σ)=0.683.
点评:解决此类问题的关键是正确理解函数表达式与正态曲线的关系,掌握函数表达式中参数的取值变化对曲线的影响.5.(2012年佛山模拟)已知随机变量X服从正态分布N(μ,σ2),且P(μ-2σ<X≤μ+2σ)=0.954 4,P(μ-σ <X≤μ+σ)=0.6 826,若μ=4,σ=1,则P(5<X<6)=( )
A.0.135 8 B.0.135 9 C.0.271 6 D.0.271 8跟踪练习1.若f(x)= ,x∈R,则下列判断中正确的是( )
A.有最大值,也有最小值 B.有最大值,无最小值
C.无最大值,有最小值 D.无最大值,也无最小值
2.正态总体N(0,1)中数值落在(-∞,-3)∪(3,+∞)的概率为( )
A.4.6% B.0.002
C.0.003 D.0.03%BC3.如右图所示是当ξ取三个不同值σ1,σ2,σ3,的三种正态曲线N(0,σ2)的图象,那么σ1,σ2,σ3的大小关系是( )
A.σ1>1>σ2>σ3>0
B.0<σ1<σ2<1<σ3
C.σ1>σ2>1>σ3>0
D.0<σ1<σ2=1<σ34.若随机变量满足正态分布N(μ,σ2),则关于正态曲线性质的叙述正确的是( )
A.σ越大,曲线越“矮胖”,σ越小,曲线越“高瘦”
B.σ越大,曲线越“高瘦”,σ越小,曲线越“矮胖”
C.σ的大小和曲线的“高瘦”、“矮胖”没有关系
D.曲线的“高瘦”、“矮胖”受到μ的影响DA5.已知随机变量ξ服从正态分布N(0,σ2),若P(ξ>2)=0.023,则P(-2≤ξ≤2)=( )
A.0.477 B.0.625 C.0.954 D.0.977解析:因为随机变量ξ服从正态分布N(0,σ2),所以正态曲线关于直线x=0对称,又P(ξ>2)=0.023,所以P(ξ<-2)=0.023,所以P(-2≤ξ≤2)=1-P(ξ>2)-P(ξ<-2)=1-2×0.023=0.954,故选C.
答案:C6.已知随机变量X服从正态分布N(2,σ2),P(X<4)=0.84,则P(X≤0)=( )
A.0.16 B.0.32 C.0.68 D.0.84A7.(2011年南开中学月考)已知随机变量ξ服从正态分布N(2,σ2)则P(ξ<2)=( )解析:由题意知平均值为2,因此P(ξ<2)= .答案:D8.已知正态总体的数据落在区间(-3,-1)里的概率和落在区间(3,5)里的概率相等,那么这个正态总体的数学期望为________.19.设X~N(0,1):
①P(-ε<X<0)=P(0<X<ε);
②P(X<0)=0.5;
③已知P(-1<X<1)=0.683,则P(X<-1)=0.158 5;
④若P(-2<X<2)=0.954,则P(X<2)=0.977;
⑤若P(-3<X<3)=0.997,则P(X<3)=0.998 5.
其中正确的有____________(填序号).①②③④⑤10.(1)已知随机变量X服从正态分布N(0,σ2),且P(-2≤X≤0)=0.4,则P(X>2)=________________.0.1(2)均值为2,标准差为 的正态分布的概率密度函数是_________________________.11.(1)随机变量X服从正态分布N(0,1),如果P(X<1)=0.841 3,求P(-1<X<0)的值;
(2)如图是正态分布N(0,1)的正态曲线图,已知P(X≤-a)=m,求图中阴影部分的面积.(3)如图所示,是一个正态曲线,试根据图象写出其正态分布密度曲线的解析式,并求出正态总体随机变量的均值和方差.解析:(1)解法一:由对称性可知
P(-1<X<0)=P(0<X<1),
而P(X<1)=0.8413,P(X≤0)=0.5,
∴P(-1<X<0)=P(X<1)-P(X≤0)=0.841 3-0.5=0.341 3.
解法二:∵P(X<1)=0.841 3,
∴P(X≥1)=P(X≤-1)=1-0.841 3=0.158 7.
P(-1<X<0)=P(0<X<1)= [1-P(X≥1)-P(X≤-
1)]= (1-2×0.158 7)=0.341 3.
(2)∵P(X≤-a)=m,由正态曲线的对称性可知:
P(X≥a)=m,从而P(-a<X<a)=1-P(X≤-a)-P(X≥a)=1-2m,
从而阴影部分的面积S= P(-a<X<a)= (1-2m)= -m.(3)从给出的正态曲线可知,该正态曲线关于直线x=20对称,最大值为 ,所以μ=20.?
由 ,解得 .?于是正态分布密度曲线的解析式是?
x∈(-∞,+∞).?
均值和方差分别是20和2.12.工厂制造的某机械零件尺寸X服从正态分布N ,问在一次正常的试验中,取1 000个零件时,不属于区间(3,5)这个尺寸范围内的零件大约多少个?
解析:不属于区间(3,5)的概率为
P(X≤3)+P(X≥5)=1-P(3<X<5)
=1-P(|X-4|<1).
因为X~N ,
所以μ=4,σ= .
所以1-P(|X-4|<1)=1-P(|X-μ|<3σ)=1-0.997=0.003.
1 000×0.003=3(个).1.求正态总体X取值小于x的概率
若X~N(μ,σ2),则P(X
(1)若X~N(μ,σ2),则由正态密度曲线的对称性可知
①P(X>μ)=P(X≤μ)= ;
②P(μ-σ
①P(X<x)+P(X<-x)=1;
②P(X<-x)=P(X>x).感谢您的使用,退出请按ESC键本小节结束
