2013-2014学年高中数学人教A版选修2-3同步辅导与检测:3.1.1线性回归方程
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-3同步辅导与检测:3.1.1线性回归方程 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 12:51:33 | ||
图片预览










文档简介
课件50张PPT。3.1 回归分析的基本思想及其初步应用3.1.1 线性回归方程统 计 案 例通过典型案例的探究,进一步了解回归分析的基本思想、方法及初步应用.基础梳理1.回归分析是对具有________的两个变量进行统计分析的一种常用方法.
例如:身高与体重有关系可以用______分析的方法来研究.( )
A.残差 B.回归
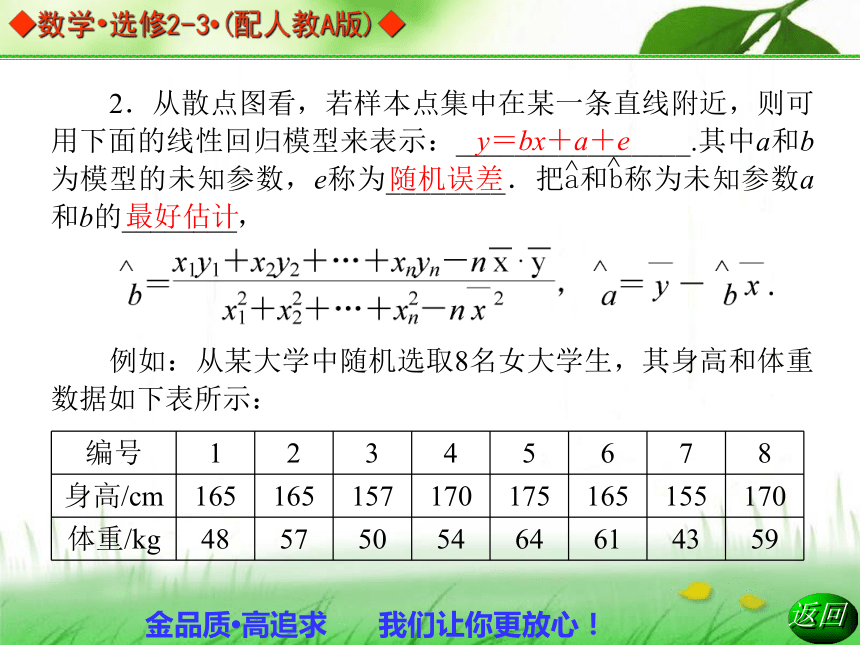
C.二维条形图 D.独立检验相关关系B2.从散点图看,若样本点集中在某一条直线附近,则可用下面的线性回归模型来表示:________________.其中a和b为模型的未知参数,e称为________.把a和b称为未知参数a和b的________,
例如:从某大学中随机选取8名女大学生,其身高和体重数据如下表所示:
^^y=bx+a+e随机误差最好估计由此建立的身高与体重的回归模型为y=0.849x-85.712,用这个模型预报一名身高为172 cm的女大学生的体重,则正确的叙述是( )
A.体重一定是60.316 kg
B.体重在60.316 kg以上
C.体重在60.316 kg左右
D.体重在60.316 kg以下3.相关系数:r= .C当r>0时,两个变量________相关;当r<0时,两个变量________相关;相关系数的绝对值越接近于1,两个变量的线性相关关系________,它们的散点图越接近________,这时用线性回归模型拟合这组数据就________.此时建立的线性回归模型是有意义的.
4.总偏差平方和、残差平方和、回归平方和、相关指数:
正负越强一条直线越好相关指数:____________________,R2的值越大,说明____________越小,模型的拟合效果________.
例如:在两个变量y与x的回归模型中,分别选择了甲、乙两个不同的模型,它们的相关指数R2如下:
则________模型拟合的效果更好. 越好残差平方和甲自测自评1.下列变量是相关关系的是( )
A.人的身高与视力
B.角的大小与所对的圆弧长
C.收入水平与消费水平
D.人的年龄与身高
2.若线性回归方程中的回归系数 b =0,则相关系数为________.^D03.(2011年长沙一中月考)在对两个变量x、y进行线性回归分析时一般有下列步骤:
①对所求出的回归方程作出解释;②收集数据(xi,yi),i=1,2,…,n;③求线性回归方程;④求相关系数;⑤根据所搜集的数据绘制散点图.如果根据可靠性要求能够判定变量x,y具有线性相关性,则在下列操作顺序中正确的是( )
A.①②⑤③④ B.③②④⑤①
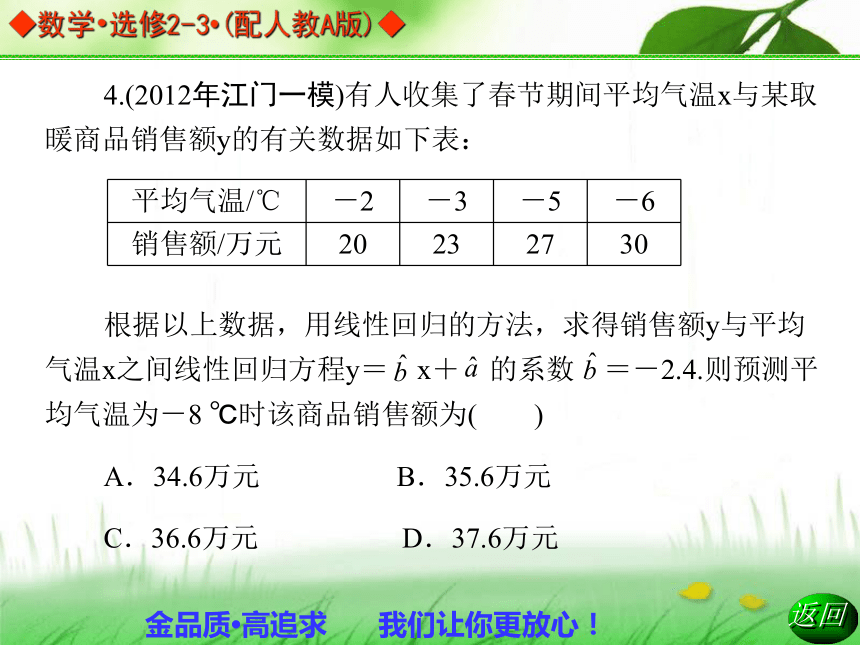
C.②④③①⑤ D.②⑤④③①D4.(2012年江门一模)有人收集了春节期间平均气温x与某取暖商品销售额y的有关数据如下表:
根据以上数据,用线性回归的方法,求得销售额y与平均气温x之间线性回归方程y= x+ 的系数 =-2.4.则预测平均气温为-8 ℃时该商品销售额为( )
A.34.6万元 B.35.6万元
C.36.6万元 D.37.6万元线性回归分析 研究某灌溉渠道水的流速y与水深x之 间的关系,测得一组数据如下:
(1)求y对x的回归直线方程;
(2)预测水深为1.95 m时水的流速是多少?分析:从散点图可以直观地看出变量x与y之间有无线性相关关系,为此把这8对数据描绘在平面直角坐标系中,得到平面上8个点,如下图所示.解析:数据列表如下:由图容易看出,x与y之间有线性相关关系.故可用线性回归模型解决.y对x的回归直线方程为y=0.694+0.733x.
回归系数b=0.733的含义是,在此灌溉渠道中,水深每增加0.1 m,水的流速平均增加0.733 m/s, a=0.694可以解释为水的流速中不受水深影响的部分.
(2)由(1)中求出的回归直线方程,把x=1.95代入,易得 y=0.694+0.733×1.95≈2.12(m/s).
计算结果表明,当水深为1.95 m时可以预测渠水的流速约为2.12 m/s.
^^^^跟踪练习1.在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
(1)画出散点图;
(2)求出y对x的回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t)解析:(1)散点图如右图所示:残差分析 假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:
(1)以x为解释变量,y为预报变量,作出散点图;
(2)求y与x之间的回归方程,并对于基本苗数56.7预报有效穗;
(3)计算各组残差,并计算残差平方和;
(4)求相关指数R2,并说明残差变量对有效穗的影响占百分之几.解析:(1)散点图如下:
(2)由图看出,样本点呈条状分布,有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系.跟踪练习2.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下:
(1)求回归方程;
(2)判断(1)中所得回归模型拟合效果如何.
解析:(1)根据表中数据作出散点图,从而可以判断出用线性回归模型来拟合数据.
计算得加工时间对零件数的线性回归方程为y=0.668x+54.93.
残差数据如下表:^^^(2)以零件数为横坐标,残差为纵坐标作出残差图如图所示:
由图可知,残差点分布较均匀,即用上述回归模型拟合数据效果很好.但需注意,由残差图也可以看出,第4个样本点和第5个样本点的残差比较大,需要确认在采集这两个样本点的过程中是否有人为的错误.非线性回归分析 某地区不同身高的未成年男性的体重平均值如下表:
试建立y与x之间的回归方程.由图看出,样本点分布在某条指数函数曲线y=c1ec2x的周围,于是令z=ln y.
解析:根据上表中的数据画出散点图如右图所示:画出散点图如下图所示.
由表中数据可得z与x之间的回归直线方程:
z=0.693+0.020x,则有 y=e0.693+0.020x.
^^跟踪练习3.若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,由例3中求出的回归方程,那么这个地区一名身高为175 cm,体重为82 kg的在校男生体重是否正常?1.对于线性相关系数r,下列说法中正确的是( )
A.|r|∈(-∞,+∞),|r|越大,相关程度越大;反之,相关程度越小
B.|r|≤1,r越大,相关程度越大;反之,相关程度越小
C.|r|≤1,且|r|越接近于1,相关程度越大;|r|越接近于0,相差程度越小
D.以上说法都不正确C2.已知回归直线方程中斜率的估计值为1.23,样本点的中心(4,5),则回归直线方程为( )
A. y=1.23x+0.08 B. y=0.08x+1.23
C. y=1.23x+4 D. y=1.23x+5^^^^AC4.①任何两个变量之间一定是线性相关的;
②线性回归方程的拟合效果与选择数据多少无关;
③函数关系一定是相关关系;
④如果样本点只有两个,则用最小二乘法计算得到的直线方程与两点式求出的方程一致.
上述说法中错误的个数是( )
A.1个 B.2个 C.3个 D.4个D5.(2011年山东卷)某产品的广告费用x与销售额y的统计数据如下表:
根据上表可得回归方程 y= bx+ a中的b为+9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元
C.67.7万元 D.72.0万元^^^^答案:B6.收集一只棉铃虫的产卵数y与温度x的几组数据后发现两个变量有相关关系,并按不同的曲线来拟合y与x之间的关系,算出了对应的相关指数R2的值如下表:B7.(2011年广东卷)某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm,170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.185则能体现A,B两个变量有更强的线性相关性的为___________________________.?
答案:丁9.在10年期间,一城市居民年收入与某种商品的销售额之间的关系见下表:(1)画出散点图;
(2)如果散点图中各点大致分布在一条直线的附近,求y与x之间的线性回归方程;
(3)试预测居民年收入50亿元时这种商品的销售额.故所求线性回归方程为 y=1.447x-15.84.
(3)根据上面求得的线性回归方程,当居民年收入50亿元时, y=1.447×50-15.84=56.51(万元),
即这种商品销售额大约为56.51万元.^^10.为了研究三月下旬的平均气温(x)与四月二十号前棉花害虫化蛹高峰日(y)的关系,某地区观察了2007年至2012年的情况,得到下面的数据:
据气象台预测,该地区在2013年三月下旬平均气温为 27 ℃,试估计2013年四月化蛹高峰日为哪天?
∴回归直线方程为 y=-2.2x+71.6.
当x=27时,y=-2.2×27+71.6=12.2.
据此,可估计该地区2013年4月12日或13日为化蛹高峰日.^^11.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=bx+a;
(3)已知该厂技术改造前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)^^解析:(1)如图:
故线性回归方程为y=0.7x+0.35.
(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为0.7×100+0.35=70.35,故耗能减少了90-70.35=19.65(吨标准煤).1.确定线性回归方程的步骤3.非线性回归问题
在大量实际问题中,研究的两个变量不一定都呈现线性相关关系,它们之间可能呈现指数关系或对数关系等非线性关系.此时可以由已知的数据画出散点图,并把散点图与已经学习过的各种函数,如幂函数、指数函数、对数函数、二次函数等作比较,挑出跟这些散点拟合最好的函数,然后再采用数量的置换,把问题转化为线性回归分析问题.如y=c1ec2x,可以通过对数变换把指数关系变为线性关系,令z=ln y则变换后样本点应该分布在直线z=bx+a(a=ln c1,b=c2)的周围.特别提醒:(1)将幂型函数y=axm(a为正的常数,x,y取正值)化为线性函数.
如果将y=axm两边同取以10为底的对数,则有
lg y=mlg x+lg a.
令u=lg y,v=lg x,lg a=b,代入上式,得u=mv+b,其中m,b是常数.这是u,v的线性函数.如果以u为纵坐标,v为横坐标,则u=mv+b的图形就是一直线.
(2)将指数型函数y=cax(a>0,c>0且为常数)化为线性函数.将y=cax两边同取以10为底的对数,有lg y=
xlg a+lg c,令lg y=u,lg a=k,lg c=b,得u=kx+b,其中,k和b是常数.感谢您的使用,退出请按ESC键本小节结束
例如:身高与体重有关系可以用______分析的方法来研究.( )
A.残差 B.回归
C.二维条形图 D.独立检验相关关系B2.从散点图看,若样本点集中在某一条直线附近,则可用下面的线性回归模型来表示:________________.其中a和b为模型的未知参数,e称为________.把a和b称为未知参数a和b的________,
例如:从某大学中随机选取8名女大学生,其身高和体重数据如下表所示:
^^y=bx+a+e随机误差最好估计由此建立的身高与体重的回归模型为y=0.849x-85.712,用这个模型预报一名身高为172 cm的女大学生的体重,则正确的叙述是( )
A.体重一定是60.316 kg
B.体重在60.316 kg以上
C.体重在60.316 kg左右
D.体重在60.316 kg以下3.相关系数:r= .C当r>0时,两个变量________相关;当r<0时,两个变量________相关;相关系数的绝对值越接近于1,两个变量的线性相关关系________,它们的散点图越接近________,这时用线性回归模型拟合这组数据就________.此时建立的线性回归模型是有意义的.
4.总偏差平方和、残差平方和、回归平方和、相关指数:
正负越强一条直线越好相关指数:____________________,R2的值越大,说明____________越小,模型的拟合效果________.
例如:在两个变量y与x的回归模型中,分别选择了甲、乙两个不同的模型,它们的相关指数R2如下:
则________模型拟合的效果更好. 越好残差平方和甲自测自评1.下列变量是相关关系的是( )
A.人的身高与视力
B.角的大小与所对的圆弧长
C.收入水平与消费水平
D.人的年龄与身高
2.若线性回归方程中的回归系数 b =0,则相关系数为________.^D03.(2011年长沙一中月考)在对两个变量x、y进行线性回归分析时一般有下列步骤:
①对所求出的回归方程作出解释;②收集数据(xi,yi),i=1,2,…,n;③求线性回归方程;④求相关系数;⑤根据所搜集的数据绘制散点图.如果根据可靠性要求能够判定变量x,y具有线性相关性,则在下列操作顺序中正确的是( )
A.①②⑤③④ B.③②④⑤①
C.②④③①⑤ D.②⑤④③①D4.(2012年江门一模)有人收集了春节期间平均气温x与某取暖商品销售额y的有关数据如下表:
根据以上数据,用线性回归的方法,求得销售额y与平均气温x之间线性回归方程y= x+ 的系数 =-2.4.则预测平均气温为-8 ℃时该商品销售额为( )
A.34.6万元 B.35.6万元
C.36.6万元 D.37.6万元线性回归分析 研究某灌溉渠道水的流速y与水深x之 间的关系,测得一组数据如下:
(1)求y对x的回归直线方程;
(2)预测水深为1.95 m时水的流速是多少?分析:从散点图可以直观地看出变量x与y之间有无线性相关关系,为此把这8对数据描绘在平面直角坐标系中,得到平面上8个点,如下图所示.解析:数据列表如下:由图容易看出,x与y之间有线性相关关系.故可用线性回归模型解决.y对x的回归直线方程为y=0.694+0.733x.
回归系数b=0.733的含义是,在此灌溉渠道中,水深每增加0.1 m,水的流速平均增加0.733 m/s, a=0.694可以解释为水的流速中不受水深影响的部分.
(2)由(1)中求出的回归直线方程,把x=1.95代入,易得 y=0.694+0.733×1.95≈2.12(m/s).
计算结果表明,当水深为1.95 m时可以预测渠水的流速约为2.12 m/s.
^^^^跟踪练习1.在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
(1)画出散点图;
(2)求出y对x的回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t)解析:(1)散点图如右图所示:残差分析 假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:
(1)以x为解释变量,y为预报变量,作出散点图;
(2)求y与x之间的回归方程,并对于基本苗数56.7预报有效穗;
(3)计算各组残差,并计算残差平方和;
(4)求相关指数R2,并说明残差变量对有效穗的影响占百分之几.解析:(1)散点图如下:
(2)由图看出,样本点呈条状分布,有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系.跟踪练习2.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得的数据如下:
(1)求回归方程;
(2)判断(1)中所得回归模型拟合效果如何.
解析:(1)根据表中数据作出散点图,从而可以判断出用线性回归模型来拟合数据.
计算得加工时间对零件数的线性回归方程为y=0.668x+54.93.
残差数据如下表:^^^(2)以零件数为横坐标,残差为纵坐标作出残差图如图所示:
由图可知,残差点分布较均匀,即用上述回归模型拟合数据效果很好.但需注意,由残差图也可以看出,第4个样本点和第5个样本点的残差比较大,需要确认在采集这两个样本点的过程中是否有人为的错误.非线性回归分析 某地区不同身高的未成年男性的体重平均值如下表:
试建立y与x之间的回归方程.由图看出,样本点分布在某条指数函数曲线y=c1ec2x的周围,于是令z=ln y.
解析:根据上表中的数据画出散点图如右图所示:画出散点图如下图所示.
由表中数据可得z与x之间的回归直线方程:
z=0.693+0.020x,则有 y=e0.693+0.020x.
^^跟踪练习3.若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,由例3中求出的回归方程,那么这个地区一名身高为175 cm,体重为82 kg的在校男生体重是否正常?1.对于线性相关系数r,下列说法中正确的是( )
A.|r|∈(-∞,+∞),|r|越大,相关程度越大;反之,相关程度越小
B.|r|≤1,r越大,相关程度越大;反之,相关程度越小
C.|r|≤1,且|r|越接近于1,相关程度越大;|r|越接近于0,相差程度越小
D.以上说法都不正确C2.已知回归直线方程中斜率的估计值为1.23,样本点的中心(4,5),则回归直线方程为( )
A. y=1.23x+0.08 B. y=0.08x+1.23
C. y=1.23x+4 D. y=1.23x+5^^^^AC4.①任何两个变量之间一定是线性相关的;
②线性回归方程的拟合效果与选择数据多少无关;
③函数关系一定是相关关系;
④如果样本点只有两个,则用最小二乘法计算得到的直线方程与两点式求出的方程一致.
上述说法中错误的个数是( )
A.1个 B.2个 C.3个 D.4个D5.(2011年山东卷)某产品的广告费用x与销售额y的统计数据如下表:
根据上表可得回归方程 y= bx+ a中的b为+9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元
C.67.7万元 D.72.0万元^^^^答案:B6.收集一只棉铃虫的产卵数y与温度x的几组数据后发现两个变量有相关关系,并按不同的曲线来拟合y与x之间的关系,算出了对应的相关指数R2的值如下表:B7.(2011年广东卷)某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm,170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为________cm.185则能体现A,B两个变量有更强的线性相关性的为___________________________.?
答案:丁9.在10年期间,一城市居民年收入与某种商品的销售额之间的关系见下表:(1)画出散点图;
(2)如果散点图中各点大致分布在一条直线的附近,求y与x之间的线性回归方程;
(3)试预测居民年收入50亿元时这种商品的销售额.故所求线性回归方程为 y=1.447x-15.84.
(3)根据上面求得的线性回归方程,当居民年收入50亿元时, y=1.447×50-15.84=56.51(万元),
即这种商品销售额大约为56.51万元.^^10.为了研究三月下旬的平均气温(x)与四月二十号前棉花害虫化蛹高峰日(y)的关系,某地区观察了2007年至2012年的情况,得到下面的数据:
据气象台预测,该地区在2013年三月下旬平均气温为 27 ℃,试估计2013年四月化蛹高峰日为哪天?
∴回归直线方程为 y=-2.2x+71.6.
当x=27时,y=-2.2×27+71.6=12.2.
据此,可估计该地区2013年4月12日或13日为化蛹高峰日.^^11.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=bx+a;
(3)已知该厂技术改造前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)^^解析:(1)如图:
故线性回归方程为y=0.7x+0.35.
(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为0.7×100+0.35=70.35,故耗能减少了90-70.35=19.65(吨标准煤).1.确定线性回归方程的步骤3.非线性回归问题
在大量实际问题中,研究的两个变量不一定都呈现线性相关关系,它们之间可能呈现指数关系或对数关系等非线性关系.此时可以由已知的数据画出散点图,并把散点图与已经学习过的各种函数,如幂函数、指数函数、对数函数、二次函数等作比较,挑出跟这些散点拟合最好的函数,然后再采用数量的置换,把问题转化为线性回归分析问题.如y=c1ec2x,可以通过对数变换把指数关系变为线性关系,令z=ln y则变换后样本点应该分布在直线z=bx+a(a=ln c1,b=c2)的周围.特别提醒:(1)将幂型函数y=axm(a为正的常数,x,y取正值)化为线性函数.
如果将y=axm两边同取以10为底的对数,则有
lg y=mlg x+lg a.
令u=lg y,v=lg x,lg a=b,代入上式,得u=mv+b,其中m,b是常数.这是u,v的线性函数.如果以u为纵坐标,v为横坐标,则u=mv+b的图形就是一直线.
(2)将指数型函数y=cax(a>0,c>0且为常数)化为线性函数.将y=cax两边同取以10为底的对数,有lg y=
xlg a+lg c,令lg y=u,lg a=k,lg c=b,得u=kx+b,其中,k和b是常数.感谢您的使用,退出请按ESC键本小节结束
