2013-2014学年高中数学人教A版选修2-3同步辅导与检测:3.1.2回归分析的应用
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-3同步辅导与检测:3.1.2回归分析的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 929.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 00:00:00 | ||
图片预览









文档简介
课件46张PPT。3.1 回归分析的基本思想及其初步应用3.1.2 回归分析的应用统 计 案 例1.通过实例进一步了解与非线性回归模型有关的一些统计思想.
2.了解判断刻画模型拟合效果的方法——相关指数和残差分析.基础梳理1.建立回归模型的基本步骤:
(1)确定研究对象,明确哪个变量是________,哪个变量是________.
(2)画出确定好的解释变量和预报变量的________,观察它们之间的关系.
(3)确定回归方程的________.
(4)按一定规则估计回归方程中的________.
(5)分析________是否有异常.解释变量预报变量散点图类型参数残差图2.指数函数模型.
样本点分布在某一条指数函数曲线y=________的周围(其中c1,c2是待定的参数),故可用指数函数模型来拟合这两个变量.
在上式两边取________,得____________________,再令z=ln y,则______________,而z与x间的关系是线性的.
3.二次函数模型.
用二次函数模型y=c3x2+c4来拟合两个变量间的关系(令 t=x2,则y=c3t+c4).
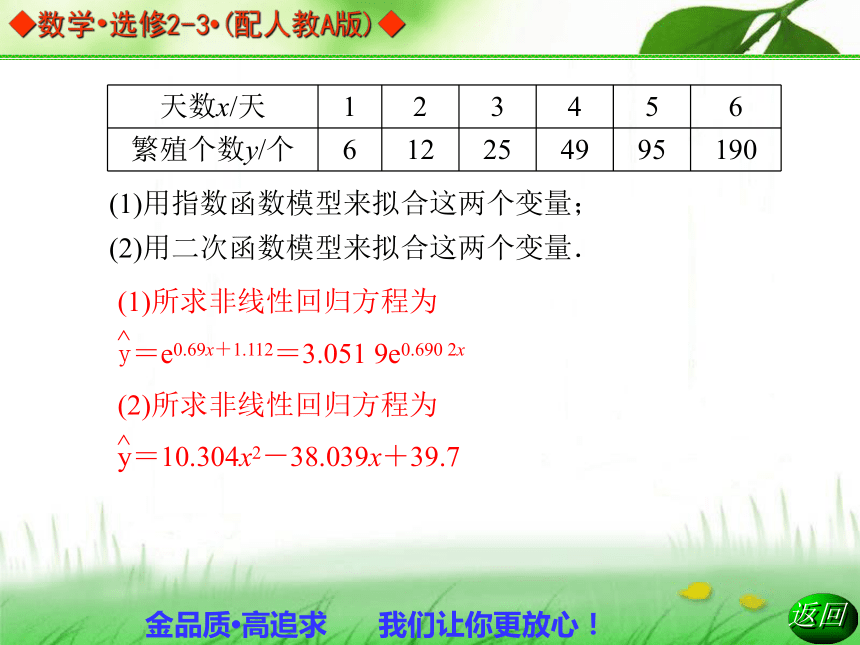
例如:为了研究某种细菌随时间x变化繁殖的个数,收集数据如下:c1ec2x对数 ln y=c2x(1+ln c1)z=c2x(1+ln c1)(1)用指数函数模型来拟合这两个变量;
(2)用二次函数模型来拟合这两个变量.(3)残差图:以________为横坐标,以__________或________,或____________等为横坐标,作出的图形称为残差图.观察残差图,如果残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高,回归方程的预报精度越高.一般4.残差分析.
(1)残差:样本值与回归值的差叫做残差,即___________.
(2)残差分析:通过________来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为________.残差残差分析残差样本编号身高数据体重估计值情况下,比较两个模型的残差比较困难(某些样本点上一个模型的残差的绝对值比另一个模型的小,而另一些样本点的情况则相反),故通过比较两个模型的残差的平方和的大小来判断模型的拟合效果.____________越小的模型,拟合的效果越好.
例如:分别用指数函数模型和二次函数模型来拟合两个变量,残差平方和分别为1 450.673和15 448.432,故选用________模型的拟合效果远远优于________模型. 残差平方和指数函数二次函数自测自评1.有下列说法:
①线性回归分析就是由样本点去寻找一条直线贴近这些样本点的数学方法;
②利用样本点的散点图可以直观判断两个变量是否具有线性关系;
③通过回归方程y=bx+a及其回归系数b,可以估计变量的取值和变化趋势;
④因为由任何一组观测值都可以求得一个回归直线方程,所以没有必要进行相关性检验.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个^^^^C2.有下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.
其中正确命题的个数是( )
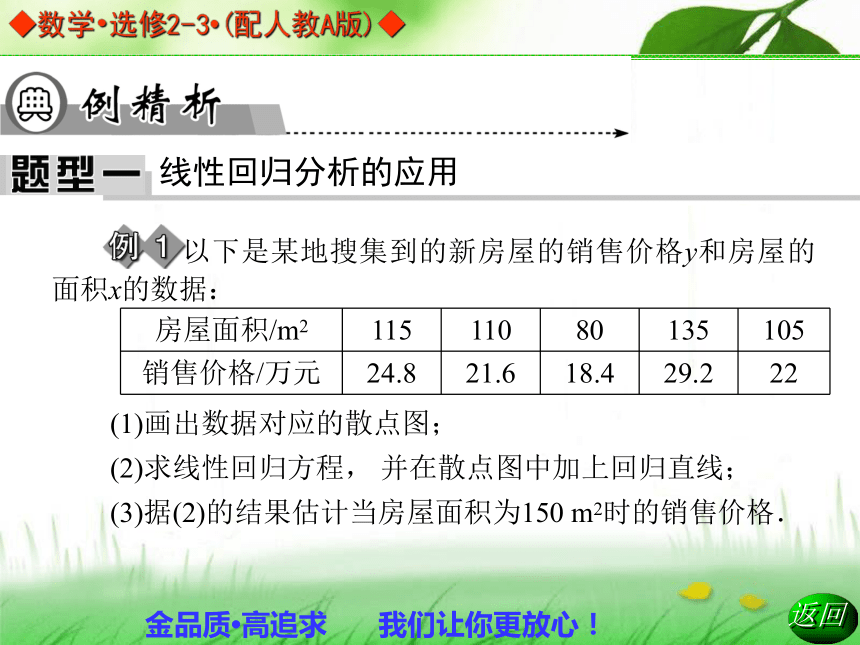
A.0个 B.1个 C.2个 D.3个3.对于回归方程y=4.75x+257,当x=28时,y的估计值是__________.^390D线性回归分析的应用 以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
(1)画出数据对应的散点图;
(2)求线性回归方程, 并在散点图中加上回归直线;
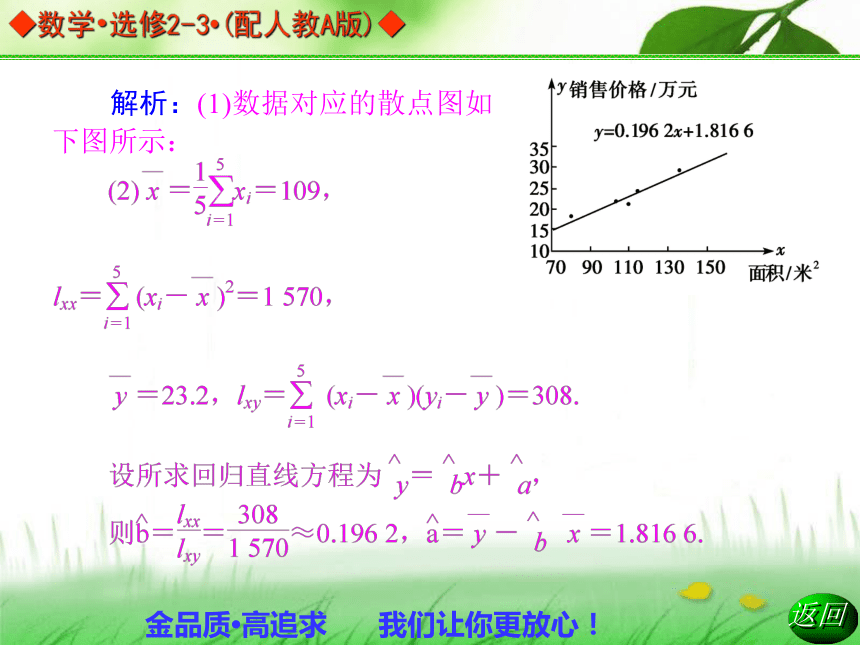
(3)据(2)的结果估计当房屋面积为150 m2时的销售价格.解析:(1)数据对应的散点图如下图所示:点评:已知x与y呈线性相关关系,就无需进行相关性检验,否则要进行相关性检验.如果两个变量不具备相关关系,或者相关关系不显著,即使求出回归方程也是毫无意义的,用其估计和预测也是不可信的.进行线性相关的判断,可通过散点图直观判断,散点图不明显的可进行相关性检验.
故所求回归直线方程为y=0.196 2x+1.816 6.
(3)据(2),当x=150 m2时,销售价格的估计值为y= 0.196 2×150+1.816 6=31.246 6(万元).^^跟踪练习1.某农场对单位面积化肥用量x(kg)和水稻相应产量y(kg)的关系作了统计,得到数据如下:
如果x与y之间具有线性相关关系,求出回归直线方程,并预测当单位面积化肥用量为32 kg时水稻的产量大约是多少?(精确到0.01 kg)解析:列表如下:y对x的回归直线方程为y=256.92+4.746x.
当x=32时,y=256.92+4.746×32≈408.79.
即回归直线方程为y=256.92+4.746x.当单位面积化肥用量为32 kg时,水稻的产量约为408.79 kg.^^^相关分析 假设关于某设备的使用年限x年和所支出的维修费用y(万元)有如下表的统计资料:
若由资料知,y对x呈线性相关关系.试求:
(1)线性回归方程y=bx+a的回归系数 a,b;
(2)求残差平方和;
(3)求相关指数R2;
(4)估计使用年限为10年时,维修费用是多少?^^^^^分析:因y对x呈线性相关关系,故用线性相关的公式分别计算.解析:(1)由已知条件制成下表:(4)回归直线方程为y=1.23x+0.08.
当x=10年时,y=1.23×10+0.08=12.38(万元).
即估计使用10年时维修费用是12.38万元.^^点评:(1)残差平方和越小,预报精确度越高.
(2)相关指数R2取得越大,说明模型的拟合效果越好.
2.有10名同学的高一数学成绩x和高二数学成绩y如下表所示:
(1)y与x是否具有相关关系?
(2)如果y与x具有相关关系,求回归直线方程.
跟踪练习1.已知两个变量x和y之间具有线性相关性,甲、乙两个同学各自独立地做了10次和15次试验,并且利用线性回归的方法求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均数都为s,对变量y的观测数据的平均数都是t,则下列说法中正确的是( )
A.l1与l2可能有交点(s,t)
B.l1与l2相交,但交点一定不是(s,t)
C.l1与l2必定平行
D.l1与l2必定重合A2.已知两个变量x和y线性相关,5次试验的观测数据如下:
那么变量y关于x的回归方程是________________.^y=0.575x-14.93. 若一组观测值(x1,y1),(x2,y2),…,(xn,yn)之间满足?yi=bxi+a+ei(i=1,2,…,n),ei恒为0,则R2为________. 14.在试验中得到变量y与x的数据如下表:
由经验知,y与 之间具有线性相关关系,试求y与x之间的回归曲线方程, 当x0=0.038时,预测y0的值.分析:通过换元转化为线性回归问题.
解析:令u= ,由题目所给数据可得下表所示的数据:5.已知某地每单位面积菜地年平均使用氮肥量x kg与每单位面积蔬菜年平均产量y t之间的关系有如下数据:
(续上表)(1)求x与y之间的相关系数,并检验是否线性相关;
(2)计算其残差,进行残差分析;
(3)计算相关指数.
6.某种产品的广告费支出x与销售额y(单位:万元)之间有如下表所示的数据.
(1)画出散点图;
(2)对两个变量进行相关性检验;
(3)求回归直线方程.
解析:(1)散点图如右图:
(2)由已知数据制成下表.∵r远大于0.75,
∴该产品的广告费支出与销售额之间存在着显著的线性相关关系.7.某工厂某产品产量与单位成本的资料如下表所示:
试根据提供的资料进行线性回归分析,并作出统计推断.
分析:这是一个回归分析问题,先求出回归方程,通过回归直线方程来分析产品产量与单位成本的关系.故回归直线方程为y=77.36-1.818 2x.
由于回归系数为b-1.818 2,由回归系数b的意义可知,产量每增加1 000件,成本下降1.818 2元.^^^8.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据为:
求出y对x的回归直线方程,并说明拟合效果的好坏.^相关系数r只能描述两个变量之间的变化方向及密切程度,但不能提示二者之间的本质联系.在解决实际问题中预报值与真实值之间会有一定的误差,引起预报值与真实值之间误差的原因有:①由公式计算的a和b为截距和斜率的估计值,它们与真实值之间存在误差;②在线性回归模型y=bx+a+e中,随机误差e的方差σ2越小,预报真实值的精度越高.
随机误差是随机变量,可以用方差σ2来衡量随机误差的大小.对于样本点(x1,y1),(x2,y2),…,(xn,yn),相应随^^感谢您的使用,退出请按ESC键本小节结束
2.了解判断刻画模型拟合效果的方法——相关指数和残差分析.基础梳理1.建立回归模型的基本步骤:
(1)确定研究对象,明确哪个变量是________,哪个变量是________.
(2)画出确定好的解释变量和预报变量的________,观察它们之间的关系.
(3)确定回归方程的________.
(4)按一定规则估计回归方程中的________.
(5)分析________是否有异常.解释变量预报变量散点图类型参数残差图2.指数函数模型.
样本点分布在某一条指数函数曲线y=________的周围(其中c1,c2是待定的参数),故可用指数函数模型来拟合这两个变量.
在上式两边取________,得____________________,再令z=ln y,则______________,而z与x间的关系是线性的.
3.二次函数模型.
用二次函数模型y=c3x2+c4来拟合两个变量间的关系(令 t=x2,则y=c3t+c4).
例如:为了研究某种细菌随时间x变化繁殖的个数,收集数据如下:c1ec2x对数 ln y=c2x(1+ln c1)z=c2x(1+ln c1)(1)用指数函数模型来拟合这两个变量;
(2)用二次函数模型来拟合这两个变量.(3)残差图:以________为横坐标,以__________或________,或____________等为横坐标,作出的图形称为残差图.观察残差图,如果残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高,回归方程的预报精度越高.一般4.残差分析.
(1)残差:样本值与回归值的差叫做残差,即___________.
(2)残差分析:通过________来判断模型拟合的效果,判断原始数据中是否存在可疑数据,这方面的分析工作称为________.残差残差分析残差样本编号身高数据体重估计值情况下,比较两个模型的残差比较困难(某些样本点上一个模型的残差的绝对值比另一个模型的小,而另一些样本点的情况则相反),故通过比较两个模型的残差的平方和的大小来判断模型的拟合效果.____________越小的模型,拟合的效果越好.
例如:分别用指数函数模型和二次函数模型来拟合两个变量,残差平方和分别为1 450.673和15 448.432,故选用________模型的拟合效果远远优于________模型. 残差平方和指数函数二次函数自测自评1.有下列说法:
①线性回归分析就是由样本点去寻找一条直线贴近这些样本点的数学方法;
②利用样本点的散点图可以直观判断两个变量是否具有线性关系;
③通过回归方程y=bx+a及其回归系数b,可以估计变量的取值和变化趋势;
④因为由任何一组观测值都可以求得一个回归直线方程,所以没有必要进行相关性检验.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个^^^^C2.有下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.
其中正确命题的个数是( )
A.0个 B.1个 C.2个 D.3个3.对于回归方程y=4.75x+257,当x=28时,y的估计值是__________.^390D线性回归分析的应用 以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
(1)画出数据对应的散点图;
(2)求线性回归方程, 并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为150 m2时的销售价格.解析:(1)数据对应的散点图如下图所示:点评:已知x与y呈线性相关关系,就无需进行相关性检验,否则要进行相关性检验.如果两个变量不具备相关关系,或者相关关系不显著,即使求出回归方程也是毫无意义的,用其估计和预测也是不可信的.进行线性相关的判断,可通过散点图直观判断,散点图不明显的可进行相关性检验.
故所求回归直线方程为y=0.196 2x+1.816 6.
(3)据(2),当x=150 m2时,销售价格的估计值为y= 0.196 2×150+1.816 6=31.246 6(万元).^^跟踪练习1.某农场对单位面积化肥用量x(kg)和水稻相应产量y(kg)的关系作了统计,得到数据如下:
如果x与y之间具有线性相关关系,求出回归直线方程,并预测当单位面积化肥用量为32 kg时水稻的产量大约是多少?(精确到0.01 kg)解析:列表如下:y对x的回归直线方程为y=256.92+4.746x.
当x=32时,y=256.92+4.746×32≈408.79.
即回归直线方程为y=256.92+4.746x.当单位面积化肥用量为32 kg时,水稻的产量约为408.79 kg.^^^相关分析 假设关于某设备的使用年限x年和所支出的维修费用y(万元)有如下表的统计资料:
若由资料知,y对x呈线性相关关系.试求:
(1)线性回归方程y=bx+a的回归系数 a,b;
(2)求残差平方和;
(3)求相关指数R2;
(4)估计使用年限为10年时,维修费用是多少?^^^^^分析:因y对x呈线性相关关系,故用线性相关的公式分别计算.解析:(1)由已知条件制成下表:(4)回归直线方程为y=1.23x+0.08.
当x=10年时,y=1.23×10+0.08=12.38(万元).
即估计使用10年时维修费用是12.38万元.^^点评:(1)残差平方和越小,预报精确度越高.
(2)相关指数R2取得越大,说明模型的拟合效果越好.
2.有10名同学的高一数学成绩x和高二数学成绩y如下表所示:
(1)y与x是否具有相关关系?
(2)如果y与x具有相关关系,求回归直线方程.
跟踪练习1.已知两个变量x和y之间具有线性相关性,甲、乙两个同学各自独立地做了10次和15次试验,并且利用线性回归的方法求得回归直线分别为l1和l2.已知两个人在试验中发现对变量x的观测数据的平均数都为s,对变量y的观测数据的平均数都是t,则下列说法中正确的是( )
A.l1与l2可能有交点(s,t)
B.l1与l2相交,但交点一定不是(s,t)
C.l1与l2必定平行
D.l1与l2必定重合A2.已知两个变量x和y线性相关,5次试验的观测数据如下:
那么变量y关于x的回归方程是________________.^y=0.575x-14.93. 若一组观测值(x1,y1),(x2,y2),…,(xn,yn)之间满足?yi=bxi+a+ei(i=1,2,…,n),ei恒为0,则R2为________. 14.在试验中得到变量y与x的数据如下表:
由经验知,y与 之间具有线性相关关系,试求y与x之间的回归曲线方程, 当x0=0.038时,预测y0的值.分析:通过换元转化为线性回归问题.
解析:令u= ,由题目所给数据可得下表所示的数据:5.已知某地每单位面积菜地年平均使用氮肥量x kg与每单位面积蔬菜年平均产量y t之间的关系有如下数据:
(续上表)(1)求x与y之间的相关系数,并检验是否线性相关;
(2)计算其残差,进行残差分析;
(3)计算相关指数.
6.某种产品的广告费支出x与销售额y(单位:万元)之间有如下表所示的数据.
(1)画出散点图;
(2)对两个变量进行相关性检验;
(3)求回归直线方程.
解析:(1)散点图如右图:
(2)由已知数据制成下表.∵r远大于0.75,
∴该产品的广告费支出与销售额之间存在着显著的线性相关关系.7.某工厂某产品产量与单位成本的资料如下表所示:
试根据提供的资料进行线性回归分析,并作出统计推断.
分析:这是一个回归分析问题,先求出回归方程,通过回归直线方程来分析产品产量与单位成本的关系.故回归直线方程为y=77.36-1.818 2x.
由于回归系数为b-1.818 2,由回归系数b的意义可知,产量每增加1 000件,成本下降1.818 2元.^^^8.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据为:
求出y对x的回归直线方程,并说明拟合效果的好坏.^相关系数r只能描述两个变量之间的变化方向及密切程度,但不能提示二者之间的本质联系.在解决实际问题中预报值与真实值之间会有一定的误差,引起预报值与真实值之间误差的原因有:①由公式计算的a和b为截距和斜率的估计值,它们与真实值之间存在误差;②在线性回归模型y=bx+a+e中,随机误差e的方差σ2越小,预报真实值的精度越高.
随机误差是随机变量,可以用方差σ2来衡量随机误差的大小.对于样本点(x1,y1),(x2,y2),…,(xn,yn),相应随^^感谢您的使用,退出请按ESC键本小节结束
