2013-2014学年高中数学人教A版选修2-3同步辅导与检测:3.2独立性检验的基本思想及其初步应用
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-3同步辅导与检测:3.2独立性检验的基本思想及其初步应用 |  | |
| 格式 | zip | ||
| 文件大小 | 645.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 12:52:23 | ||
图片预览









文档简介
课件36张PPT。3.2 独立性检验的基本思想及其初步应用统 计 案 例1.通过对典型案例(如“肺癌与吸烟有关吗”等)的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用.
2.通过对典型案例(如“质量控制”、“新药是否有效”等)的探究,了解实际推断原理和假设检验的基本思想、方法及初步应用.基础梳理1.列联表:分类变量的汇总统计表(频数表).一般我们只研究每个分类变量只取两个值,这样的列联表称为2×2列联表.
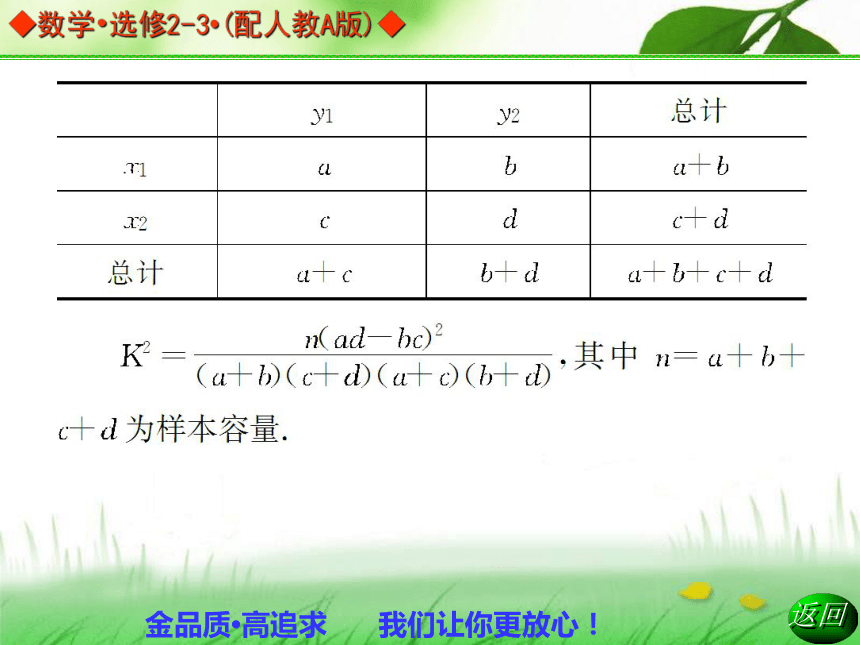
一般地,假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:2.三维柱形图和二维条形图.
若要推断的论述为H1:“X与Y有关系”,可以按如下步骤判断结论H1成立的可能性:
(1)在三维柱形图中,主对角线上两个柱形高度的乘积ad与副对角线上两个柱形高度的乘积bc相差________,H1成立的可能性就________.
(2)在二维条形图中,计算 和 ,两个值相差________,H1成立的可能性就________.
例如:在三维柱形图中,主对角线上两个柱形高度的乘积与副对角线上两个柱形高度的乘积相差越大两个变量有关系的可能性就( )
A.越大 B.越小
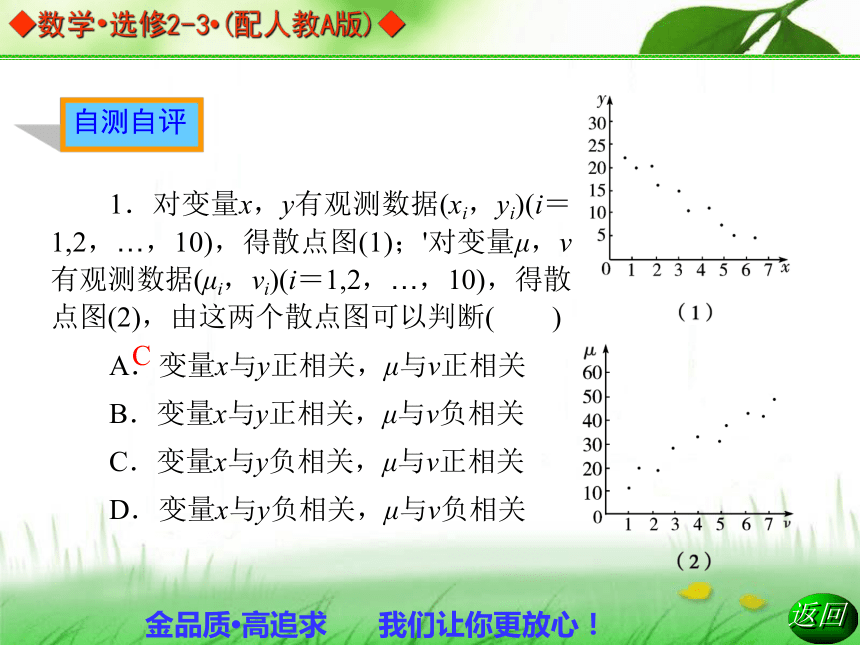
C.无法判断 D.以上都不对越大越大越大越大A自测自评1.对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);'对变量μ,ν有观测数据(μi,νi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
A.变量x与y正相关,μ与ν正相关
B.变量x与y正相关,μ与ν负相关
C.变量x与y负相关,μ与ν正相关
D.变量x与y负相关,μ与ν负相关CC2.相关系数的绝对值接近1时,说明两变量相关关系的密切程度是( )
A.不相关 B.微弱相关
C.高度相关 D.不确定3. 对于分类变量X与Y的随机变量K2的观测值k,下列说法正确的是(??)
A. k越大,推断“X与Y有关系”,犯错误的概率越大
B. k越小,推断“X与Y有关系”,犯错误的概率越大
C. k越接近于0,推断“X与Y无关”,犯错误的概率越大
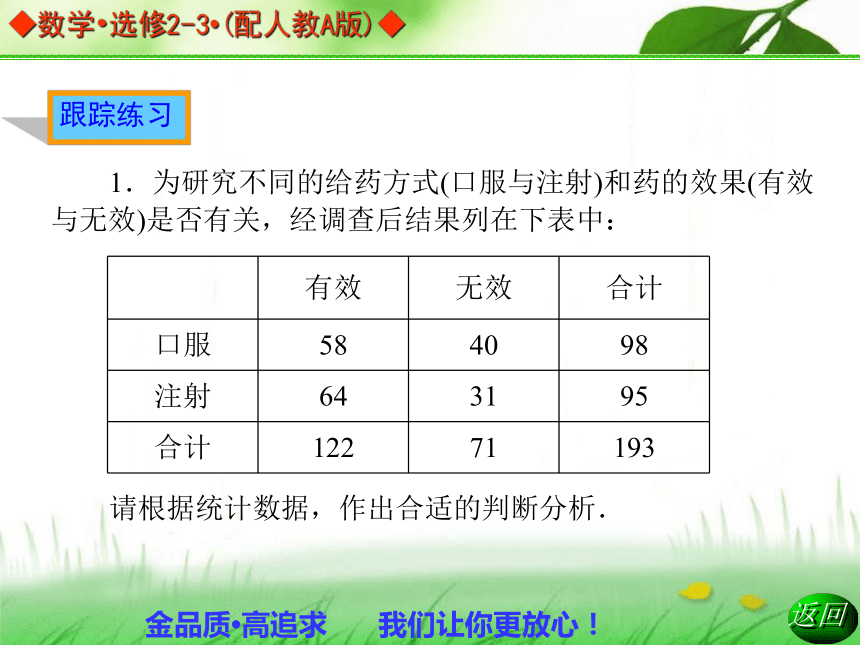
D. k越大,推断“X与Y无关”,犯错误的概率越小B有关、无关的检验 磨牙不仅影响别人休息,而且可能与患某种疾病有关,下表是一次调查所得的数据,试问:每晚都磨牙与肠道中有寄生虫有关吗?跟踪练习1.为研究不同的给药方式(口服与注射)和药的效果(有效与无效)是否有关,经调查后结果列在下表中:
请根据统计数据,作出合适的判断分析.解析:由公式得
K2= ≈ 1.390.
∵1.390<3.841,
∴我们有理由说“口服与注射”与“有效与无效”无关,即不能作出药的效果与给药方式有关的结论. 为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.试分析学生选报文、理科与对外语的兴趣是否有关?解析:根据题目所给的数据得到如下列联表:根据列联表中数据由公式计算得
K2= ≈1.871×10-4.
因为1.871×10-4<2.706,所以据目前的数据不能认为学生选报文、理科与对外语的兴趣有关,即可以认为学生选报文、理科与对外语的兴趣无关.
点评:进行独立性检验时,通常有以下几个步骤:?
①根据数据绘制成表格;?
②根据公式求出K2值?
③比较K2与临界值的关系;?
④作出统计推断.跟踪练习2.某单位餐厅的固定餐椅经常有损坏,于是该单位领导决定在餐厅墙壁上张贴文明标语看是否有效果,并对文明标语张贴前后餐椅的损坏情况作了一个统计,具体数据如下:解析:根据题中的数据计算:
因为1.78<2.706,所以我们没有理由说在餐厅墙壁上张贴文明标语对减少餐椅损坏数有效果,即效果不明显.问:我们是否有理由说在餐厅墙壁上张贴文明标语对减少餐椅损坏有效果?独立性检验的综合应用 某企业有两间分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两间分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
乙厂:(1)分别估计两间分厂生产的零件的优质品率;
(2)由以上统计数据填写2×2列联表,并问是否有99%的把握认为“两间分厂生产的零件的质量有差异”.解析:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为 =72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为 =64%.(2)
由列联表中的数据,得K2的观测值为
K2=
≈7.353>6.635.
所以有99%的把握认为“两间分厂生产的零件的质量有差异”.
跟踪练习3.某生产线上,质量监督员甲在生产现场时,990件产品中有合格品982件,次品8件;不在生产现场时,510件产品中有合格品493件,次品17件.能否有99%的把握认为质量监督员甲在不在场与产品质量好坏有关系?
解析:根据题目所给数据得如下2×2列联表:由列联表中的数据,得K2的观测值为
K2=
≈13.097>6.635.
因此,有99%的把握认为质量监督员甲在不在生产现场与产品质量好坏有关系.1.与表格相比,能更直观地反映出相关数据总体状况的是( )
A.列联表 B.散点图
C.残差图 D.三维柱形图和二维条形图D2.如果有99%的把握认为“X与Y有关系”,那么具体算出的数据满足( )
A.k>6.635 B.k>5.024
C.k>7.879 D.k>3.8413.(2011年湖南卷)通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:A附表:
参照附表,得到的正确结论是( )
A.有99%以上的把握认为“爱好该项运动与性别有关”
B.有99%以上的把握认为“爱好该项运动与性别无关”C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”解析:由K2≈7.8>6.635,则P(K2≥6.635)=0.010,故由独立性检验的意义可知选A.
答案:A4.某调查机构调查教师工作压力大小的情况,部分数据如表:则推断“工作压力大与不喜欢教师职业有关系”,这种推断犯错误的概率不超过(??)
A. 0.01 B. 0.05 C. 0.10 D. 0.005 B5.在研究某种新措施对猪白痢的防治效果问题时,得到了以下数据.
试问新措施对防治猪白痢是否有效?解析:由公式得,
k= ≈7.317.
由于7.317>6.635,所以我们有99%的把握认为新措施对防治猪白痢是有效的.6.为了研究色盲与性别的关系,共调查了1 000人,结果如下表所示:
试问:色盲与性别有无关系?解析:由公式得,
k= ≈27.139.
由于27.139>10.828,所以我们有99.9%的把握认为色盲与性别是有关的.7.为了解决初二平面几何入门难的问题,某校在初中一年级代数教学中加强概念和推理教学,并设有对照班,下表是初中二年级平面几何期中测验成绩统计表的一部分,试分析研究实验结果.解析:∵k= ≈160.234>10.828,
故有99.9%的把握认为“在初一加强概念和推理教学,对初二平面几何的测试成绩”有关系.8.在500个人身上试验某种血清对预防感冒的作用,把一年中的记录与另外500个未用血清的人作比较,结果如下表所示:
试画出列联表的条形图,并通过图形判断这种血清能否起到预防感冒的作用?并进行独立性检验.
分析:作出二维条形图判断.
解析:如图所示:
由公式得,
k=
≈3.143.
从条形图看,这种血清对预防感冒有作用.由于k>2.706,我们有90%的把握认为起作用.9.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若K2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99%人患有肺病
B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病
C.若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推判出现错误
D.以上三种说法都不正确C1.在列联表中注意事件的对应及有关值的确定,避免混乱.
2.若要求判断X与Y有关时,先假设X与Y无关.
3.因为三维柱形图和二维条形图所表示的关系只是一种粗略的估计,不能够精确地给出所得结论的可信程度,因而不常用.并且在实际问题的解决中也较为繁琐,故在判断两个分类变量的关系的可靠性时一般利用随机变量K2来确定.
4.在实际问题中,独立性检验的结论也仅仅是一种数学关系,得到的结论也可能犯错误,比如,在推测吸烟与患肺病是否有关时,通过收集、整理、分析数据,我们得到“吸烟与患肺病有关”的结论并且有超过99%的把握说明吸烟与患肺病有关系,或者说这个结论出错的概率为0.01以下,但实际上一个人吸烟,也不一定会患肺病,患肺病也不一定是由吸烟引起的,这是数学中的统计思维与确定性思维差异的反映.但我们可以利用统计分析的结果去预测实际问题的结果.
5.把计算出的K2的值与相关的临界值作比较,确定出“X与Y有关系”的有把握程度.
感谢您的使用,退出请按ESC键本小节结束
2.通过对典型案例(如“质量控制”、“新药是否有效”等)的探究,了解实际推断原理和假设检验的基本思想、方法及初步应用.基础梳理1.列联表:分类变量的汇总统计表(频数表).一般我们只研究每个分类变量只取两个值,这样的列联表称为2×2列联表.
一般地,假设有两个分类变量X和Y,它们的值域分别为{x1,x2}和{y1,y2},其样本频数列联表(称为2×2列联表)为:2.三维柱形图和二维条形图.
若要推断的论述为H1:“X与Y有关系”,可以按如下步骤判断结论H1成立的可能性:
(1)在三维柱形图中,主对角线上两个柱形高度的乘积ad与副对角线上两个柱形高度的乘积bc相差________,H1成立的可能性就________.
(2)在二维条形图中,计算 和 ,两个值相差________,H1成立的可能性就________.
例如:在三维柱形图中,主对角线上两个柱形高度的乘积与副对角线上两个柱形高度的乘积相差越大两个变量有关系的可能性就( )
A.越大 B.越小
C.无法判断 D.以上都不对越大越大越大越大A自测自评1.对变量x,y有观测数据(xi,yi)(i=1,2,…,10),得散点图(1);'对变量μ,ν有观测数据(μi,νi)(i=1,2,…,10),得散点图(2),由这两个散点图可以判断( )
A.变量x与y正相关,μ与ν正相关
B.变量x与y正相关,μ与ν负相关
C.变量x与y负相关,μ与ν正相关
D.变量x与y负相关,μ与ν负相关CC2.相关系数的绝对值接近1时,说明两变量相关关系的密切程度是( )
A.不相关 B.微弱相关
C.高度相关 D.不确定3. 对于分类变量X与Y的随机变量K2的观测值k,下列说法正确的是(??)
A. k越大,推断“X与Y有关系”,犯错误的概率越大
B. k越小,推断“X与Y有关系”,犯错误的概率越大
C. k越接近于0,推断“X与Y无关”,犯错误的概率越大
D. k越大,推断“X与Y无关”,犯错误的概率越小B有关、无关的检验 磨牙不仅影响别人休息,而且可能与患某种疾病有关,下表是一次调查所得的数据,试问:每晚都磨牙与肠道中有寄生虫有关吗?跟踪练习1.为研究不同的给药方式(口服与注射)和药的效果(有效与无效)是否有关,经调查后结果列在下表中:
请根据统计数据,作出合适的判断分析.解析:由公式得
K2= ≈ 1.390.
∵1.390<3.841,
∴我们有理由说“口服与注射”与“有效与无效”无关,即不能作出药的效果与给药方式有关的结论. 为了探究学生选报文、理科是否与对外语的兴趣有关,某同学调查了361名高二在校学生,调查结果如下:理科对外语有兴趣的有138人,无兴趣的有98人,文科对外语有兴趣的有73人,无兴趣的有52人.试分析学生选报文、理科与对外语的兴趣是否有关?解析:根据题目所给的数据得到如下列联表:根据列联表中数据由公式计算得
K2= ≈1.871×10-4.
因为1.871×10-4<2.706,所以据目前的数据不能认为学生选报文、理科与对外语的兴趣有关,即可以认为学生选报文、理科与对外语的兴趣无关.
点评:进行独立性检验时,通常有以下几个步骤:?
①根据数据绘制成表格;?
②根据公式求出K2值?
③比较K2与临界值的关系;?
④作出统计推断.跟踪练习2.某单位餐厅的固定餐椅经常有损坏,于是该单位领导决定在餐厅墙壁上张贴文明标语看是否有效果,并对文明标语张贴前后餐椅的损坏情况作了一个统计,具体数据如下:解析:根据题中的数据计算:
因为1.78<2.706,所以我们没有理由说在餐厅墙壁上张贴文明标语对减少餐椅损坏数有效果,即效果不明显.问:我们是否有理由说在餐厅墙壁上张贴文明标语对减少餐椅损坏有效果?独立性检验的综合应用 某企业有两间分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两间分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
乙厂:(1)分别估计两间分厂生产的零件的优质品率;
(2)由以上统计数据填写2×2列联表,并问是否有99%的把握认为“两间分厂生产的零件的质量有差异”.解析:(1)甲厂抽查的产品中有360件优质品,从而甲厂生产的零件的优质品率估计为 =72%;
乙厂抽查的产品中有320件优质品,从而乙厂生产的零件的优质品率估计为 =64%.(2)
由列联表中的数据,得K2的观测值为
K2=
≈7.353>6.635.
所以有99%的把握认为“两间分厂生产的零件的质量有差异”.
跟踪练习3.某生产线上,质量监督员甲在生产现场时,990件产品中有合格品982件,次品8件;不在生产现场时,510件产品中有合格品493件,次品17件.能否有99%的把握认为质量监督员甲在不在场与产品质量好坏有关系?
解析:根据题目所给数据得如下2×2列联表:由列联表中的数据,得K2的观测值为
K2=
≈13.097>6.635.
因此,有99%的把握认为质量监督员甲在不在生产现场与产品质量好坏有关系.1.与表格相比,能更直观地反映出相关数据总体状况的是( )
A.列联表 B.散点图
C.残差图 D.三维柱形图和二维条形图D2.如果有99%的把握认为“X与Y有关系”,那么具体算出的数据满足( )
A.k>6.635 B.k>5.024
C.k>7.879 D.k>3.8413.(2011年湖南卷)通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:A附表:
参照附表,得到的正确结论是( )
A.有99%以上的把握认为“爱好该项运动与性别有关”
B.有99%以上的把握认为“爱好该项运动与性别无关”C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”解析:由K2≈7.8>6.635,则P(K2≥6.635)=0.010,故由独立性检验的意义可知选A.
答案:A4.某调查机构调查教师工作压力大小的情况,部分数据如表:则推断“工作压力大与不喜欢教师职业有关系”,这种推断犯错误的概率不超过(??)
A. 0.01 B. 0.05 C. 0.10 D. 0.005 B5.在研究某种新措施对猪白痢的防治效果问题时,得到了以下数据.
试问新措施对防治猪白痢是否有效?解析:由公式得,
k= ≈7.317.
由于7.317>6.635,所以我们有99%的把握认为新措施对防治猪白痢是有效的.6.为了研究色盲与性别的关系,共调查了1 000人,结果如下表所示:
试问:色盲与性别有无关系?解析:由公式得,
k= ≈27.139.
由于27.139>10.828,所以我们有99.9%的把握认为色盲与性别是有关的.7.为了解决初二平面几何入门难的问题,某校在初中一年级代数教学中加强概念和推理教学,并设有对照班,下表是初中二年级平面几何期中测验成绩统计表的一部分,试分析研究实验结果.解析:∵k= ≈160.234>10.828,
故有99.9%的把握认为“在初一加强概念和推理教学,对初二平面几何的测试成绩”有关系.8.在500个人身上试验某种血清对预防感冒的作用,把一年中的记录与另外500个未用血清的人作比较,结果如下表所示:
试画出列联表的条形图,并通过图形判断这种血清能否起到预防感冒的作用?并进行独立性检验.
分析:作出二维条形图判断.
解析:如图所示:
由公式得,
k=
≈3.143.
从条形图看,这种血清对预防感冒有作用.由于k>2.706,我们有90%的把握认为起作用.9.在吸烟与患肺病这两个分类变量的计算中,下列说法正确的是( )
A.若K2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99%人患有肺病
B.从独立性检验可知有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患有肺病
C.若从统计量中求出有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推判出现错误
D.以上三种说法都不正确C1.在列联表中注意事件的对应及有关值的确定,避免混乱.
2.若要求判断X与Y有关时,先假设X与Y无关.
3.因为三维柱形图和二维条形图所表示的关系只是一种粗略的估计,不能够精确地给出所得结论的可信程度,因而不常用.并且在实际问题的解决中也较为繁琐,故在判断两个分类变量的关系的可靠性时一般利用随机变量K2来确定.
4.在实际问题中,独立性检验的结论也仅仅是一种数学关系,得到的结论也可能犯错误,比如,在推测吸烟与患肺病是否有关时,通过收集、整理、分析数据,我们得到“吸烟与患肺病有关”的结论并且有超过99%的把握说明吸烟与患肺病有关系,或者说这个结论出错的概率为0.01以下,但实际上一个人吸烟,也不一定会患肺病,患肺病也不一定是由吸烟引起的,这是数学中的统计思维与确定性思维差异的反映.但我们可以利用统计分析的结果去预测实际问题的结果.
5.把计算出的K2的值与相关的临界值作比较,确定出“X与Y有关系”的有把握程度.
感谢您的使用,退出请按ESC键本小节结束
