2013-2014学年高中数学人教A版选修2-1同步辅导与检测:2.1.2求曲线的方程
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-1同步辅导与检测:2.1.2求曲线的方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 501.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 00:00:00 | ||
图片预览








文档简介
课件22张PPT。2.1 曲线与方程
2.1.2 求曲线的方程 圆锥曲线与方程 1.会根据图形建立适当的坐标系.
2.会用直接法求简单的曲线方程.基础梳理1.设P点的坐标为(x,y),点P到点M(-1,2)的距离为__________________.
2.设P点的坐标为(x,y),点P到x轴的距离为______.
3.设P点的坐标为(x,y),点P到直线x-y+1=0的距离为________.
4.已知两点A(-2,0),P(x,y),则 =________________.
5.已知 =(x,y-1), =(2,4),则 = ______________.|y| (-2-x,-y) 2x+4(y-1) 自测自评1.已知A(2,5)、B(3,-1),则线段AB的方程是( )
A.6x+y-17=0
B.6x+y-17=0(x≥3)
C.6x+y-17=0(x≤3)
D.6x+y-17=0(2≤x≤3)
2.若点M到两坐标轴的距离的积为2011,则点M的轨迹方程是( )
A.xy=2011 B.xy=-2011
C.xy=±2011 D.xy=±2011(x>0)D C 3.已知A(-1,0),B(2,4),△ABC的面积为10,则动点C的轨迹方程是( )
A.4x-3y-16=0或4x-3y+16=0
B.4x-3y-16=0或4x-3y+24=0
C.4x-3y+16=0或4x-3y+24=0
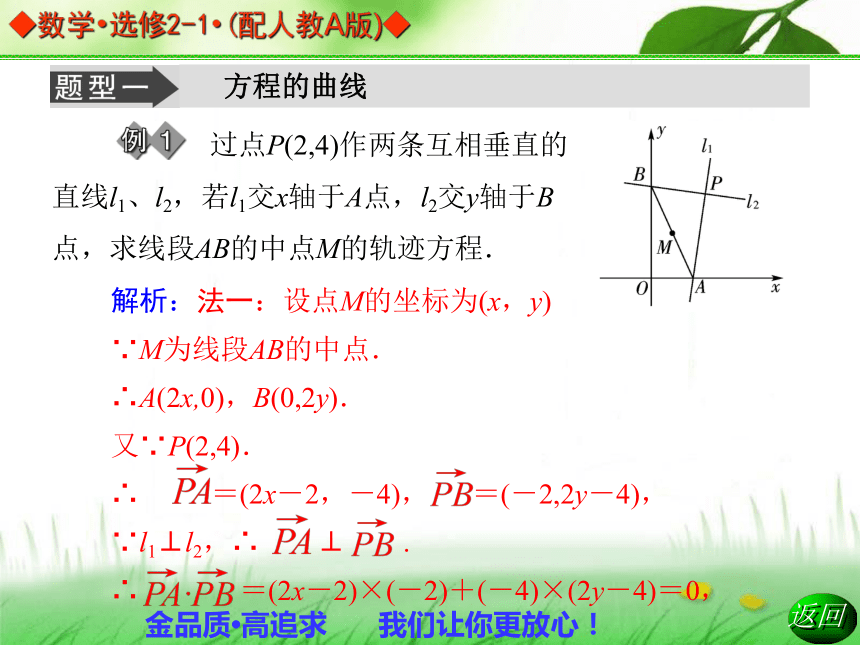
D.4x-3y+16=0或4x-3y-24=0B 方程的曲线 过点P(2,4)作两条互相垂直的直线l1、l2,若l1交x轴于A点,l2交y轴于B点,求线段AB的中点M的轨迹方程.解析:法一:设点M的坐标为(x,y)
∵M为线段AB的中点.
∴A(2x,0),B(0,2y).
又∵P(2,4).
∴ =(2x-2,-4), =(-2,2y-4),
∵l1⊥l2,∴ ⊥ .
∴ =(2x-2)×(-2)+(-4)×(2y-4)=0,即x+2y-5=0.
∴M点的轨迹方程是x+2y-5=0.
法二:设M的坐标为(x,y),则A、B两点的坐标分别是(2x,0)、(0,2y),连结PM.
∵l1⊥l2,∴2|PM|=|AB|.跟踪训练1.若A、B两点的坐标分别是(1,0)、(-1,0),且kMA·kMB=-1,则动点M的轨迹方程是什么?答案:x2+y2=1(x≠±1)求曲线的方程(题目中已有坐标系) 设A、B两点的坐标是(0,0),(2,2),求线段AB的垂直平分线的方程.
解析:设M(x,y)是线段AB的垂直平分线上任意一点,也就是点M属于集合
P={M︱ |MA|=|MB|}.
由两点间的距离公式,点M所适合条件可表示为:
=
将上式两边平方,整理得:
x+y=2①
我们证明方程①是线段AB的垂直平分线的方程.(1)由求方程的过程可知,垂直平分线上每一点的坐标都是方程①解;
(2)设点M1的坐标(x1,y1)是方程①的解,即
x1+y1=2,x1=2-y1.
点M1到A、B的距离分别是
∴|M1A|=|M1B|
即点M1在线段AB的垂直平分线上.
由(1)、(2)可知方程①是线段AB的垂直平分线的方程.
点评:一般在高中阶段第二段证明可以省略,如有特殊情况,可适当予以说明.跟踪训练2.已知一曲线在x轴上方,它上面的每一点到点A(0,2)的距离减去它到x轴的距离的差都是2,求这条曲线的方程.分析:设出动点坐标,利用两点间的距离公式得到点A的距离,再减去x轴的距离,利用差为2列出等式,即可以整理出方程.
解析:设曲线上任一点的坐标为M(x,y),作MB⊥x轴,B为垂足,则点M属于集合P={M||MA|-|MB|=2}.
由距离公式,点M适合的条件可表示为
-y=2,化简得x2=8y.
∵曲线在x轴上方,∴y>0.
显然(0,0)是这个方程的解,但不属于已知曲线.
∴所求曲线的方程为x2=8y(y≠0).求曲线的方程(题目中没有坐标系) 两个定点A、B的距离为4,求到这两点距离平方之和等于16的点M的轨迹方程.
解析:以AB所在直线为x轴,AB的中垂线为y轴建立直角坐标系
设M点的坐标为(x,y),A(-2,0),B(2,0)
依题意:|MA|2+|MB|2=16,
即(x+2)2+y2+(x-2)2+y2=16,
化简得x2+y2=4.
所以M的轨迹方程为x2+y2=4.跟踪训练3.已知△ABC中,三边c>b>a,且a、b、c成等差数列,b=2,试求点B的轨迹方程.解析:如下图,以AC所在的直线为x轴,AC的垂直平分线为y轴建立平面直角坐标系.
由于b=|AC|=2,
则A点坐标为(-1,0),C点坐标为(1,0).
因为a、b、c成等差数列,
所以2b=a+c.
即4=|BC|+|AB|.
设B点坐标为(x,y),一、选择填空题
1.点A(3,-4)、B(-2,2)是否在方程x2+y2=25表示的圆上?
__________________________________________.A在圆上 B不在圆上 D 求曲线(图形)的方程,一般有下面几个步骤:
(1)建立适当的坐标系,用有序实数对(x,y)表示曲线上任意一点M的坐标;
(2)写出适合条件P的点M的集合P={M|P(M)};
(3)用坐标表示条件P(M),列出方程f(x,y)=0;
(4)化方程f(x,y)=0为最简形式;
(5)证明以化简后的方程的解为坐标的点都是曲线上的点.
说明:一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写,如有特殊情况,可适当予以说明.另外,根据情况,也可以省略步骤(2),直接列出曲线方程,建立的坐标系如果不同则方程一般也不一样.祝您学业有成
2.1.2 求曲线的方程 圆锥曲线与方程 1.会根据图形建立适当的坐标系.
2.会用直接法求简单的曲线方程.基础梳理1.设P点的坐标为(x,y),点P到点M(-1,2)的距离为__________________.
2.设P点的坐标为(x,y),点P到x轴的距离为______.
3.设P点的坐标为(x,y),点P到直线x-y+1=0的距离为________.
4.已知两点A(-2,0),P(x,y),则 =________________.
5.已知 =(x,y-1), =(2,4),则 = ______________.|y| (-2-x,-y) 2x+4(y-1) 自测自评1.已知A(2,5)、B(3,-1),则线段AB的方程是( )
A.6x+y-17=0
B.6x+y-17=0(x≥3)
C.6x+y-17=0(x≤3)
D.6x+y-17=0(2≤x≤3)
2.若点M到两坐标轴的距离的积为2011,则点M的轨迹方程是( )
A.xy=2011 B.xy=-2011
C.xy=±2011 D.xy=±2011(x>0)D C 3.已知A(-1,0),B(2,4),△ABC的面积为10,则动点C的轨迹方程是( )
A.4x-3y-16=0或4x-3y+16=0
B.4x-3y-16=0或4x-3y+24=0
C.4x-3y+16=0或4x-3y+24=0
D.4x-3y+16=0或4x-3y-24=0B 方程的曲线 过点P(2,4)作两条互相垂直的直线l1、l2,若l1交x轴于A点,l2交y轴于B点,求线段AB的中点M的轨迹方程.解析:法一:设点M的坐标为(x,y)
∵M为线段AB的中点.
∴A(2x,0),B(0,2y).
又∵P(2,4).
∴ =(2x-2,-4), =(-2,2y-4),
∵l1⊥l2,∴ ⊥ .
∴ =(2x-2)×(-2)+(-4)×(2y-4)=0,即x+2y-5=0.
∴M点的轨迹方程是x+2y-5=0.
法二:设M的坐标为(x,y),则A、B两点的坐标分别是(2x,0)、(0,2y),连结PM.
∵l1⊥l2,∴2|PM|=|AB|.跟踪训练1.若A、B两点的坐标分别是(1,0)、(-1,0),且kMA·kMB=-1,则动点M的轨迹方程是什么?答案:x2+y2=1(x≠±1)求曲线的方程(题目中已有坐标系) 设A、B两点的坐标是(0,0),(2,2),求线段AB的垂直平分线的方程.
解析:设M(x,y)是线段AB的垂直平分线上任意一点,也就是点M属于集合
P={M︱ |MA|=|MB|}.
由两点间的距离公式,点M所适合条件可表示为:
=
将上式两边平方,整理得:
x+y=2①
我们证明方程①是线段AB的垂直平分线的方程.(1)由求方程的过程可知,垂直平分线上每一点的坐标都是方程①解;
(2)设点M1的坐标(x1,y1)是方程①的解,即
x1+y1=2,x1=2-y1.
点M1到A、B的距离分别是
∴|M1A|=|M1B|
即点M1在线段AB的垂直平分线上.
由(1)、(2)可知方程①是线段AB的垂直平分线的方程.
点评:一般在高中阶段第二段证明可以省略,如有特殊情况,可适当予以说明.跟踪训练2.已知一曲线在x轴上方,它上面的每一点到点A(0,2)的距离减去它到x轴的距离的差都是2,求这条曲线的方程.分析:设出动点坐标,利用两点间的距离公式得到点A的距离,再减去x轴的距离,利用差为2列出等式,即可以整理出方程.
解析:设曲线上任一点的坐标为M(x,y),作MB⊥x轴,B为垂足,则点M属于集合P={M||MA|-|MB|=2}.
由距离公式,点M适合的条件可表示为
-y=2,化简得x2=8y.
∵曲线在x轴上方,∴y>0.
显然(0,0)是这个方程的解,但不属于已知曲线.
∴所求曲线的方程为x2=8y(y≠0).求曲线的方程(题目中没有坐标系) 两个定点A、B的距离为4,求到这两点距离平方之和等于16的点M的轨迹方程.
解析:以AB所在直线为x轴,AB的中垂线为y轴建立直角坐标系
设M点的坐标为(x,y),A(-2,0),B(2,0)
依题意:|MA|2+|MB|2=16,
即(x+2)2+y2+(x-2)2+y2=16,
化简得x2+y2=4.
所以M的轨迹方程为x2+y2=4.跟踪训练3.已知△ABC中,三边c>b>a,且a、b、c成等差数列,b=2,试求点B的轨迹方程.解析:如下图,以AC所在的直线为x轴,AC的垂直平分线为y轴建立平面直角坐标系.
由于b=|AC|=2,
则A点坐标为(-1,0),C点坐标为(1,0).
因为a、b、c成等差数列,
所以2b=a+c.
即4=|BC|+|AB|.
设B点坐标为(x,y),一、选择填空题
1.点A(3,-4)、B(-2,2)是否在方程x2+y2=25表示的圆上?
__________________________________________.A在圆上 B不在圆上 D 求曲线(图形)的方程,一般有下面几个步骤:
(1)建立适当的坐标系,用有序实数对(x,y)表示曲线上任意一点M的坐标;
(2)写出适合条件P的点M的集合P={M|P(M)};
(3)用坐标表示条件P(M),列出方程f(x,y)=0;
(4)化方程f(x,y)=0为最简形式;
(5)证明以化简后的方程的解为坐标的点都是曲线上的点.
说明:一般情况下,化简前后方程的解集是相同的,步骤(5)可以省略不写,如有特殊情况,可适当予以说明.另外,根据情况,也可以省略步骤(2),直接列出曲线方程,建立的坐标系如果不同则方程一般也不一样.祝您学业有成
