2013-2014学年高中数学人教A版选修2-1同步辅导与检测:2.3.2双曲线的简单几何性质1
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-1同步辅导与检测:2.3.2双曲线的简单几何性质1 |

|
|
| 格式 | zip | ||
| 文件大小 | 513.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 21:12:46 | ||
图片预览






文档简介
课件27张PPT。圆锥曲线与方程 2.3 双曲线
2.3.2 双曲线的简单几何性质(一)1.了解双曲线的实际背景,了解双曲线在刻画现实世界和解决实际问题中的作用.
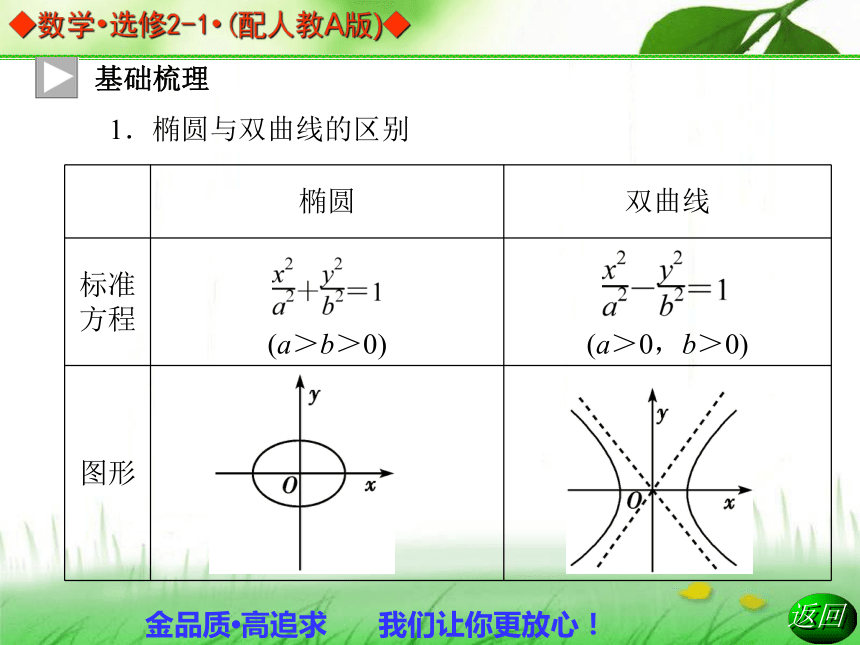
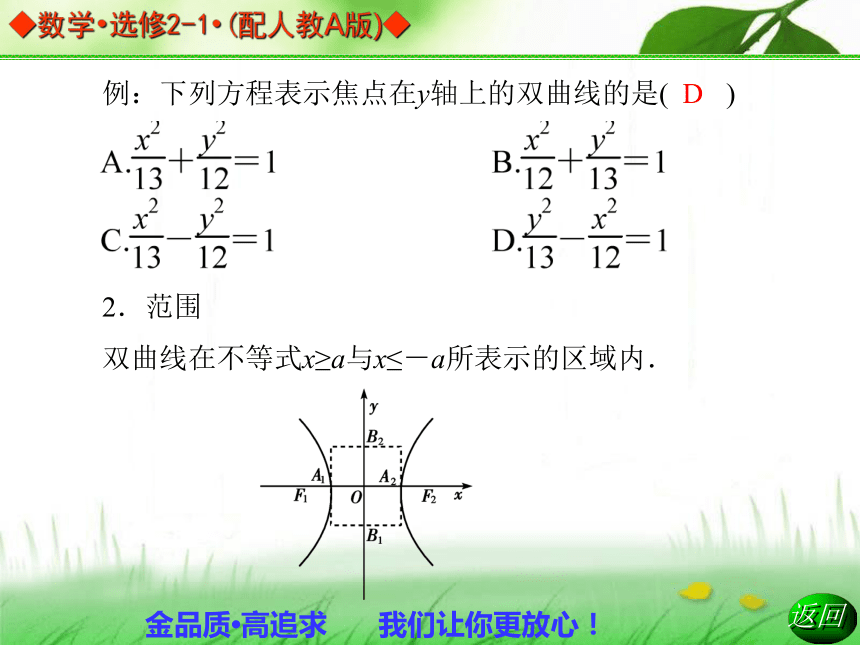
2.了解双曲线的简单性质.基础梳理1.椭圆与双曲线的区别 例:下列方程表示焦点在y轴上的双曲线的是( )2.范围
双曲线在不等式x≥a与x≤-a所表示的区域内.D 例:双曲线 上的点的横坐标x的取值范围是( )
A.|x|≥3 B.x≥4
C.|x|≥4 D.R
3.对称性
双曲线关于每个坐标轴和原点都对称,这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心,双曲线的对称中心叫双曲线的中心.
例:方程x2-|xy|+3y2=8的曲线对称性错误的是( )
A.原点 B.x轴 C.y轴 D.直线y=xD D 4.顶点
双曲线和它的对称轴有两个交点A1(-a,0)、A2(a,0),它们叫做双曲线的顶点.
线段A1A2叫双曲线的实轴,它的长等于2a,a叫做双曲线的实半轴长;线段B1B2叫双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.
5.渐近线
把两条直线y=± x叫做双曲线的渐近线.解析:由双曲线方程可得焦点在x轴上,
a=4,b=3.
∴渐近线方程为y=± x=± x.
答案:A自测自评1.双曲线 的( )
A.实轴长为2 ,虚轴长为4,渐近线方程为y= ± x,离心率e=
B.实轴长为2 ,虚轴长为4,渐近线方程为y= ± x,离心率e=
C.实轴长为2 ,虚轴长为4,渐近线方程为y=± 2 x,离心率e=
D.实轴长为2 ,虚轴长为8,渐近线方程为y= ± x,离心率e=A 2.若双曲线 (a>0)的离心率为2,则a等于( )
A.2 B.
C. D.1
3.双曲线 的焦点到渐近线的距离为( )
A.2 B.2
C. D.1D A 已知双曲线的标准方程求其几何性质 求双曲线nx2-my2=mn(m>0,n>0)的半实轴长,半虚轴长,焦点坐标,离心率,顶点坐标和渐近线方程.跟踪训练1.已知双曲线 -y2=1,则其渐近线方程为______,离心率为________. 由双曲线的几何性质求标准方程 求适合下列条件的双曲线的标准方程.
(1)虚轴长为12,离心率为 ,焦点在x轴上;
(2)求与双曲线x2-2y2=2有公共渐近线,且过点
M(2,-2)的双曲线方程.
解析:(1)设双曲线的标准方程为
(a>0,b>0)
由题设知:2b=12, = ,且c2=a2+b2
∴b=6,c=10,a=8,
∴所求的双曲线标准方程为 .(2)设与双曲线 -y2=1有公共渐进线的双曲线方程为 -y2=λ(λ≠0)
将点M(2,-2)代入 -y2=λ(λ≠0)得:λ=-2
∴所求的双曲线标准方程为 .
点评:求双曲线的方程关键是寻找两个关于a,b,c的等式,加上a,b,c本身的关系式则可求满足条件的双曲线方程.若已知此双曲线的渐进线方程为 ,则可设双曲线方程为 =λ(λ≠0).跟踪训练2.双曲线的渐近线方程为x±2y=0,焦距为10,该双曲线的方程为____________.求双曲线的离心率 设双曲线 (0<a<b)的半焦距为c,直线l过(a,0)、(0,b)两点,且原点到直线l的距离为 c,求双曲线的离心率.
解析:直线l的方程为bx+ay-ab=0,
由点到直线的距离公式,且b>a>0,跟踪训练3.过双曲线的一个焦点F2作垂直于实轴的弦PQ,F1是另一焦点,若∠PF1Q= ,则双曲线的离心率e等于( )
A. -1 B.
C. +1 D. +2A 双曲线 (a>0,b>0)性质如下:
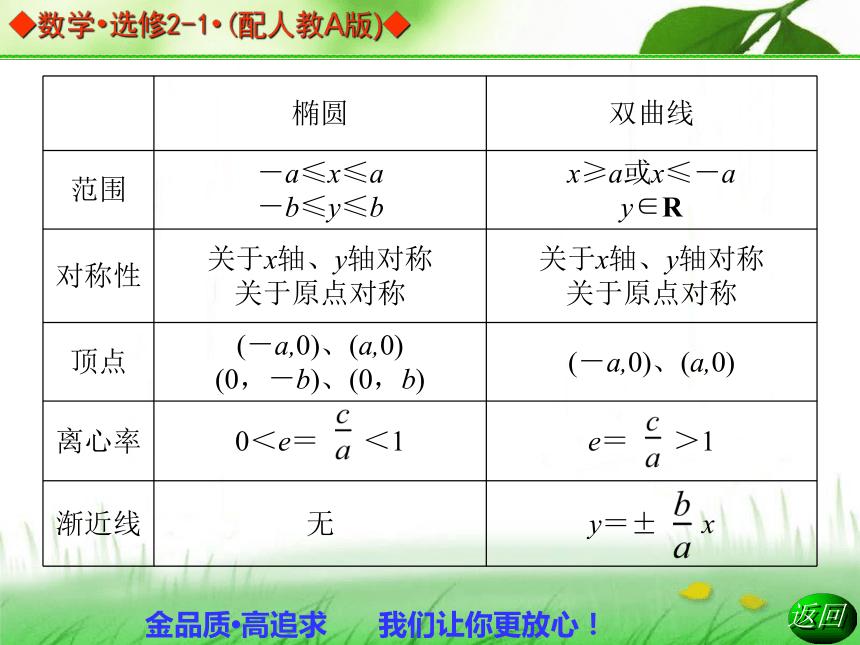
1.范围:|x|≥a,y∈R.
2.对称性:关于x、y轴均对称,关于原点中心对称.
3.顶点:轴端点A1(-a,0),A2(a,0).
4.渐近线:y= x,y=- x.
5.离心率:e= ∈(1,+∞).祝您学业有成
2.3.2 双曲线的简单几何性质(一)1.了解双曲线的实际背景,了解双曲线在刻画现实世界和解决实际问题中的作用.
2.了解双曲线的简单性质.基础梳理1.椭圆与双曲线的区别 例:下列方程表示焦点在y轴上的双曲线的是( )2.范围
双曲线在不等式x≥a与x≤-a所表示的区域内.D 例:双曲线 上的点的横坐标x的取值范围是( )
A.|x|≥3 B.x≥4
C.|x|≥4 D.R
3.对称性
双曲线关于每个坐标轴和原点都对称,这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心,双曲线的对称中心叫双曲线的中心.
例:方程x2-|xy|+3y2=8的曲线对称性错误的是( )
A.原点 B.x轴 C.y轴 D.直线y=xD D 4.顶点
双曲线和它的对称轴有两个交点A1(-a,0)、A2(a,0),它们叫做双曲线的顶点.
线段A1A2叫双曲线的实轴,它的长等于2a,a叫做双曲线的实半轴长;线段B1B2叫双曲线的虚轴,它的长等于2b,b叫做双曲线的虚半轴长.
5.渐近线
把两条直线y=± x叫做双曲线的渐近线.解析:由双曲线方程可得焦点在x轴上,
a=4,b=3.
∴渐近线方程为y=± x=± x.
答案:A自测自评1.双曲线 的( )
A.实轴长为2 ,虚轴长为4,渐近线方程为y= ± x,离心率e=
B.实轴长为2 ,虚轴长为4,渐近线方程为y= ± x,离心率e=
C.实轴长为2 ,虚轴长为4,渐近线方程为y=± 2 x,离心率e=
D.实轴长为2 ,虚轴长为8,渐近线方程为y= ± x,离心率e=A 2.若双曲线 (a>0)的离心率为2,则a等于( )
A.2 B.
C. D.1
3.双曲线 的焦点到渐近线的距离为( )
A.2 B.2
C. D.1D A 已知双曲线的标准方程求其几何性质 求双曲线nx2-my2=mn(m>0,n>0)的半实轴长,半虚轴长,焦点坐标,离心率,顶点坐标和渐近线方程.跟踪训练1.已知双曲线 -y2=1,则其渐近线方程为______,离心率为________. 由双曲线的几何性质求标准方程 求适合下列条件的双曲线的标准方程.
(1)虚轴长为12,离心率为 ,焦点在x轴上;
(2)求与双曲线x2-2y2=2有公共渐近线,且过点
M(2,-2)的双曲线方程.
解析:(1)设双曲线的标准方程为
(a>0,b>0)
由题设知:2b=12, = ,且c2=a2+b2
∴b=6,c=10,a=8,
∴所求的双曲线标准方程为 .(2)设与双曲线 -y2=1有公共渐进线的双曲线方程为 -y2=λ(λ≠0)
将点M(2,-2)代入 -y2=λ(λ≠0)得:λ=-2
∴所求的双曲线标准方程为 .
点评:求双曲线的方程关键是寻找两个关于a,b,c的等式,加上a,b,c本身的关系式则可求满足条件的双曲线方程.若已知此双曲线的渐进线方程为 ,则可设双曲线方程为 =λ(λ≠0).跟踪训练2.双曲线的渐近线方程为x±2y=0,焦距为10,该双曲线的方程为____________.求双曲线的离心率 设双曲线 (0<a<b)的半焦距为c,直线l过(a,0)、(0,b)两点,且原点到直线l的距离为 c,求双曲线的离心率.
解析:直线l的方程为bx+ay-ab=0,
由点到直线的距离公式,且b>a>0,跟踪训练3.过双曲线的一个焦点F2作垂直于实轴的弦PQ,F1是另一焦点,若∠PF1Q= ,则双曲线的离心率e等于( )
A. -1 B.
C. +1 D. +2A 双曲线 (a>0,b>0)性质如下:
1.范围:|x|≥a,y∈R.
2.对称性:关于x、y轴均对称,关于原点中心对称.
3.顶点:轴端点A1(-a,0),A2(a,0).
4.渐近线:y= x,y=- x.
5.离心率:e= ∈(1,+∞).祝您学业有成
