2013-2014学年高中数学人教A版选修2-1同步辅导与检测:2.4.1抛物线及其标准方程
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-1同步辅导与检测:2.4.1抛物线及其标准方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 455.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-05 00:00:00 | ||
图片预览







文档简介
课件23张PPT。圆锥曲线与方程 2.4 抛物线
2.4.1 抛物线及其标准方程1.了解抛物线的实际背景,了解抛物线在刻画现实世界和解决实际问题中的作用.
2.掌握抛物线的定义、几何图形、标准方程.基础梳理1.抛物线的定义:平面内与一个定点F和一条不过该定点的定直线l的距离相等的点的轨迹叫抛物线,点F叫抛物线的焦点,直线l叫做抛物线的准线.
例:点M与点F(4,0)的距离等于它到直线l:x+4=0的距离,点M的轨迹是( )
A.圆 B.椭圆
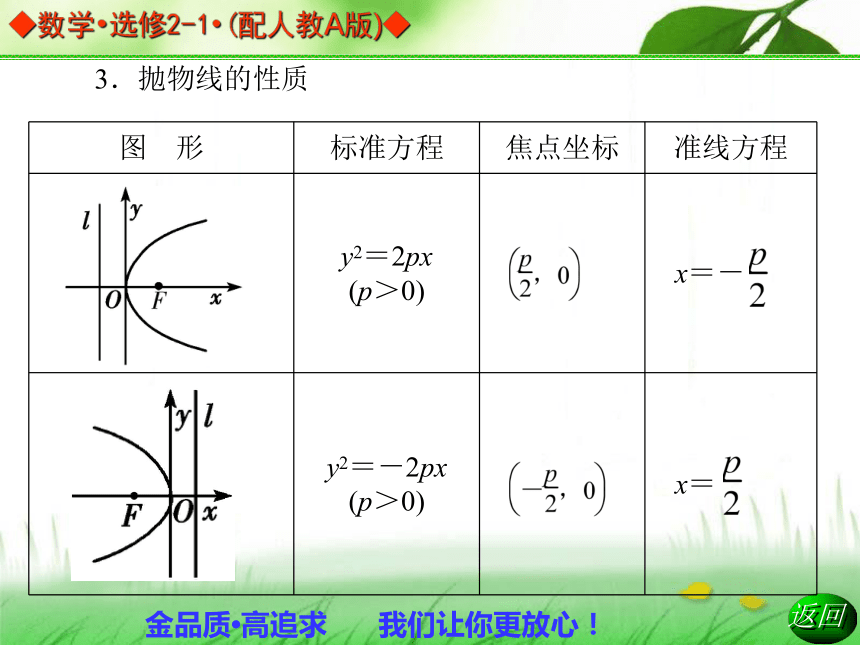
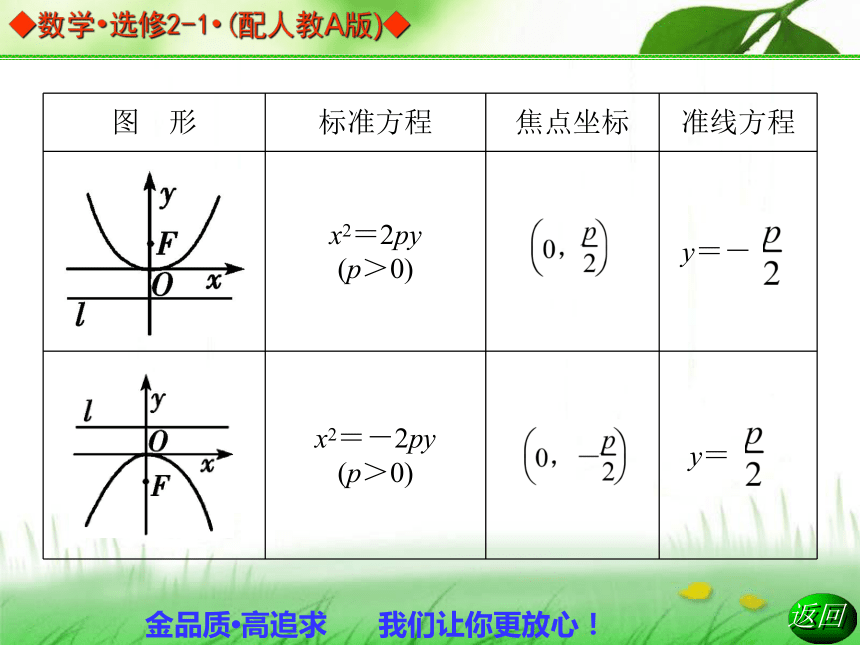
C.双曲线 D.抛物线D 2.如右图所示,建立直角坐标系xOy,使x轴经过点F且垂直于直线l,垂足为K,并使原点与线段KF的中点重合,得抛物线的标准方程为y2=2px,它表示的抛物线的焦点在x轴的正半轴上,坐标是 ,它的准线方程是x=- .3.抛物线的性质4.已知抛物线y= x2,则它的焦点坐标是( )
D 自测自评1.已知曲线C:y2=2px上一点P的横坐标为4,P到焦点的距离为5,则曲线C的焦点到准线的距离为( )
A. B.1 C.2 D.4
2.抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标是( )
3.准线方程为x=1的抛物线的标准方程是( )
A.y2=-2x B.y2=-4x
C.y2=-2x D.y2=4xC B B 求下列抛物线的焦点坐标和准线方程 求下列抛物线的焦点坐标和准线方程:
(1)y2=-14x;(2)5x2-2y=0;(3)y2=ax(a>0).
解析:(1)因为p=7,所以焦点坐标是 ,
准线方程是x= .
(2)抛物线方程化为标准形式为x2= y,因为p= ,
所以焦点坐标是 ,准线方程是y=- .
(3)由a>0知p= ,所以焦点坐标是 ,准线方程是x=- .跟踪训练1.求抛物线y=ax2(a≠0)的焦点坐标和准线方程.答案:求抛物线的标准方程 分别求满足下列条件的抛物线的标准方程.
(1)过点(3,-4);
(2)焦点在直线x+3y+15=0上.
解析:(1)法一:∵点(3,-4)在第四象限,
∴抛物线的标准方程为y2=2px(p>0)或x2=-2p1y(p1>0).
把点(3,-4)的坐标分别代入y2=2px和x2=-2p1y,得(-4)2=2p·3,32=-2p1·(-4).跟踪训练2.根据下列条件写出抛物线的标准方程:
(1)准线方程为y=-1;
(2)焦点在x轴的正半轴上,焦点到准线的距离是3.答案:(1)x2=4y (2)y2=6x抛物线定义的应用 抛物线y2=8x上一点P到其焦点的距离为9,求点P的坐标.
解析:点P到其焦点的距离等于点P到其准线x=-2的距离,得xP=7,yP=±2 ,点P的坐标为(7,±2 ).跟踪训练3.已知点P是抛物线y2=2x上的一个动点,求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.解析:由抛物线的定义可知,抛物线上的点到准线的距离等于到焦点的距离,由图可知,P点,(0,2)点,和抛物线的焦点( ,0)三点共线时距离之和最小,所以最小距离一、选择填空题
1.经过点P(2,4)的抛物线的标准方程是( )
A.y2=8x B.x2=y
C.y2=8x或x2=y D.无法确定
解析:假设抛物线的方程是y2=2px或x2=2py,将点P的坐标代入求解.
答案:C
2.抛物线y2=10x的焦点到准线的距离是( )
A. B.5 C. D.10B 1.抛物线定义是解决抛物线问题的重要工具,一般涉及焦点或准线的问题均要首先考虑定义的使用.
2.求抛物线问题要十分慎重地考察焦点在什么位置,以便确定方程的形式.
3.建系求抛物线方程一般要以过焦点与准线垂直的直线为x轴,以焦点和焦点在准线上的射影之间的线段中垂线为y轴.
4.注意焦点到原点的距离为2p的四分之一.
5.注意定义中的焦点不在准线上.祝您学业有成
2.4.1 抛物线及其标准方程1.了解抛物线的实际背景,了解抛物线在刻画现实世界和解决实际问题中的作用.
2.掌握抛物线的定义、几何图形、标准方程.基础梳理1.抛物线的定义:平面内与一个定点F和一条不过该定点的定直线l的距离相等的点的轨迹叫抛物线,点F叫抛物线的焦点,直线l叫做抛物线的准线.
例:点M与点F(4,0)的距离等于它到直线l:x+4=0的距离,点M的轨迹是( )
A.圆 B.椭圆
C.双曲线 D.抛物线D 2.如右图所示,建立直角坐标系xOy,使x轴经过点F且垂直于直线l,垂足为K,并使原点与线段KF的中点重合,得抛物线的标准方程为y2=2px,它表示的抛物线的焦点在x轴的正半轴上,坐标是 ,它的准线方程是x=- .3.抛物线的性质4.已知抛物线y= x2,则它的焦点坐标是( )
D 自测自评1.已知曲线C:y2=2px上一点P的横坐标为4,P到焦点的距离为5,则曲线C的焦点到准线的距离为( )
A. B.1 C.2 D.4
2.抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标是( )
3.准线方程为x=1的抛物线的标准方程是( )
A.y2=-2x B.y2=-4x
C.y2=-2x D.y2=4xC B B 求下列抛物线的焦点坐标和准线方程 求下列抛物线的焦点坐标和准线方程:
(1)y2=-14x;(2)5x2-2y=0;(3)y2=ax(a>0).
解析:(1)因为p=7,所以焦点坐标是 ,
准线方程是x= .
(2)抛物线方程化为标准形式为x2= y,因为p= ,
所以焦点坐标是 ,准线方程是y=- .
(3)由a>0知p= ,所以焦点坐标是 ,准线方程是x=- .跟踪训练1.求抛物线y=ax2(a≠0)的焦点坐标和准线方程.答案:求抛物线的标准方程 分别求满足下列条件的抛物线的标准方程.
(1)过点(3,-4);
(2)焦点在直线x+3y+15=0上.
解析:(1)法一:∵点(3,-4)在第四象限,
∴抛物线的标准方程为y2=2px(p>0)或x2=-2p1y(p1>0).
把点(3,-4)的坐标分别代入y2=2px和x2=-2p1y,得(-4)2=2p·3,32=-2p1·(-4).跟踪训练2.根据下列条件写出抛物线的标准方程:
(1)准线方程为y=-1;
(2)焦点在x轴的正半轴上,焦点到准线的距离是3.答案:(1)x2=4y (2)y2=6x抛物线定义的应用 抛物线y2=8x上一点P到其焦点的距离为9,求点P的坐标.
解析:点P到其焦点的距离等于点P到其准线x=-2的距离,得xP=7,yP=±2 ,点P的坐标为(7,±2 ).跟踪训练3.已知点P是抛物线y2=2x上的一个动点,求点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值.解析:由抛物线的定义可知,抛物线上的点到准线的距离等于到焦点的距离,由图可知,P点,(0,2)点,和抛物线的焦点( ,0)三点共线时距离之和最小,所以最小距离一、选择填空题
1.经过点P(2,4)的抛物线的标准方程是( )
A.y2=8x B.x2=y
C.y2=8x或x2=y D.无法确定
解析:假设抛物线的方程是y2=2px或x2=2py,将点P的坐标代入求解.
答案:C
2.抛物线y2=10x的焦点到准线的距离是( )
A. B.5 C. D.10B 1.抛物线定义是解决抛物线问题的重要工具,一般涉及焦点或准线的问题均要首先考虑定义的使用.
2.求抛物线问题要十分慎重地考察焦点在什么位置,以便确定方程的形式.
3.建系求抛物线方程一般要以过焦点与准线垂直的直线为x轴,以焦点和焦点在准线上的射影之间的线段中垂线为y轴.
4.注意焦点到原点的距离为2p的四分之一.
5.注意定义中的焦点不在准线上.祝您学业有成
