2013-2014学年高中数学人教A版选修2-1同步辅导与检测:3.1.2空间向量的数乘运算
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-1同步辅导与检测:3.1.2空间向量的数乘运算 |  | |
| 格式 | zip | ||
| 文件大小 | 506.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-05 06:30:46 | ||
图片预览








文档简介
课件23张PPT。3.1 空间向量及其运算
3.1.2 空间向量的数乘运算空间向量与立体几何 1.运用空间向量解决立体几何中的问题.
2.理解共线向量定理和共面向量定理及它们的推论.基础梳理1.共线的向量(或平行的向量)是指__________.
2.共线向量定理:当a≠0时,a∥b?存在实数λ,使________________;
3.平行于__________的向量,叫做共面向量.
例 空间任意两个向量总是__________.
4.共面向量定理:如果两个向量a,b不共线,则向量c与向量a,b共面的充要条件是:存在唯一的有序实数对(x,y),使________________.1.方向相同或相反的非零向量
2.b=λa
3.同一平面 例:共面的 4.c=xa+yb自测自评1.直三棱柱ABC-A1B1C1中,若 =a, =b, =c,则 等于( )
A.a+b-c B.a-b+c
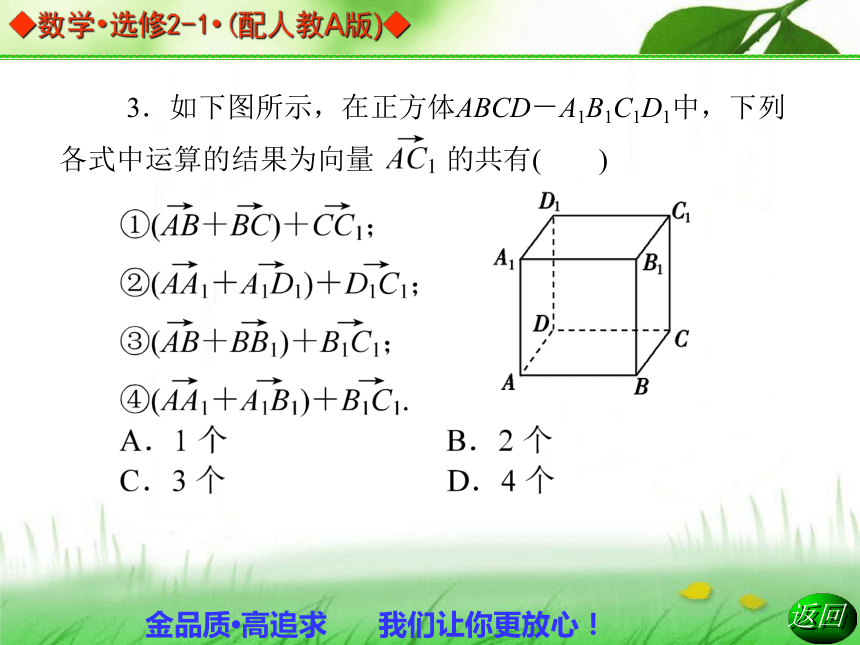
C.-a+b+c D.-a+b-cD 3.如下图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算的结果为向量 的共有( )向量共线问题 如图所示,四边形ABCD,ABEF都是平行四边形且不共面,M、N分别是AC、BF的中点,判断 与 是否共线?跟踪训练2 向量共面问题 对于任意空间四边形ABCD,E、F分别是AB、CD的中点.
试证: 与 、 共面.跟踪训练2.已知P是平面四边形ABCD所在平面外一点,连结PA、PB、PC、PD,如图所示,点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心,求证:E、F、G、H四点共面.分析:由共面向量定理可知,要证明E、F、G、H四点共面,只要证明存在有序实数对x、y使 即可;要证明平面EFGH∥平面ABCD,只要证明平面EG内两条直线平行于平面AC内的两条相交直线即可.证明:分别延长PE、PF、PG、PH交对边于M、N、Q、R.
∵E、F、G、H分别是所在三角形的重心.
∴M、N、Q、R为所在边的中点,顺次连结M、N、Q、R 所得四边形为平行四边形.且有一、选择填空题
1.下列命题中正确的个数是( )
①若a与b共线,b与c共线,则a与c共线
②向量a、b、c共面即它们所在的直线共面
③若a∥b,则存在惟一的实数λ,使a=λb
A.1 B.2
C.3 D.0解析:①中若b=0,则a与c不一定共线.②中共面向量的定义是平行于同一平面的向量,表示这些向量的有向线段所在的直线不一定共面.③中若b=0,a≠0,则不存在λ.
答案:D2.当|a|=|b|≠0,且a、b不共线时,a+b与a-b的关系是( )
A.共面 B.不共面
C.共线 D.无法确定解析:由加法法则知,a+b与a-b可以是菱形的对角线.
答案:A用好已有的定理及推论:如共线向量定理、共面向量定理及推论等,并能运用它们证明空间向量的共线和共面的问题.祝您学业有成
3.1.2 空间向量的数乘运算空间向量与立体几何 1.运用空间向量解决立体几何中的问题.
2.理解共线向量定理和共面向量定理及它们的推论.基础梳理1.共线的向量(或平行的向量)是指__________.
2.共线向量定理:当a≠0时,a∥b?存在实数λ,使________________;
3.平行于__________的向量,叫做共面向量.
例 空间任意两个向量总是__________.
4.共面向量定理:如果两个向量a,b不共线,则向量c与向量a,b共面的充要条件是:存在唯一的有序实数对(x,y),使________________.1.方向相同或相反的非零向量
2.b=λa
3.同一平面 例:共面的 4.c=xa+yb自测自评1.直三棱柱ABC-A1B1C1中,若 =a, =b, =c,则 等于( )
A.a+b-c B.a-b+c
C.-a+b+c D.-a+b-cD 3.如下图所示,在正方体ABCD-A1B1C1D1中,下列各式中运算的结果为向量 的共有( )向量共线问题 如图所示,四边形ABCD,ABEF都是平行四边形且不共面,M、N分别是AC、BF的中点,判断 与 是否共线?跟踪训练2 向量共面问题 对于任意空间四边形ABCD,E、F分别是AB、CD的中点.
试证: 与 、 共面.跟踪训练2.已知P是平面四边形ABCD所在平面外一点,连结PA、PB、PC、PD,如图所示,点E、F、G、H分别为△PAB、△PBC、△PCD、△PDA的重心,求证:E、F、G、H四点共面.分析:由共面向量定理可知,要证明E、F、G、H四点共面,只要证明存在有序实数对x、y使 即可;要证明平面EFGH∥平面ABCD,只要证明平面EG内两条直线平行于平面AC内的两条相交直线即可.证明:分别延长PE、PF、PG、PH交对边于M、N、Q、R.
∵E、F、G、H分别是所在三角形的重心.
∴M、N、Q、R为所在边的中点,顺次连结M、N、Q、R 所得四边形为平行四边形.且有一、选择填空题
1.下列命题中正确的个数是( )
①若a与b共线,b与c共线,则a与c共线
②向量a、b、c共面即它们所在的直线共面
③若a∥b,则存在惟一的实数λ,使a=λb
A.1 B.2
C.3 D.0解析:①中若b=0,则a与c不一定共线.②中共面向量的定义是平行于同一平面的向量,表示这些向量的有向线段所在的直线不一定共面.③中若b=0,a≠0,则不存在λ.
答案:D2.当|a|=|b|≠0,且a、b不共线时,a+b与a-b的关系是( )
A.共面 B.不共面
C.共线 D.无法确定解析:由加法法则知,a+b与a-b可以是菱形的对角线.
答案:A用好已有的定理及推论:如共线向量定理、共面向量定理及推论等,并能运用它们证明空间向量的共线和共面的问题.祝您学业有成
