2013-2014学年高中数学人教A版选修2-1同步辅导与检测:3.1.3空间向量的数量积运算
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-1同步辅导与检测:3.1.3空间向量的数量积运算 |  | |
| 格式 | zip | ||
| 文件大小 | 461.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-05 06:29:21 | ||
图片预览








文档简介
课件23张PPT。3.1 空间向量及其运算
3.1.3 空间向量的数量积运算空间向量与立体几何 1.掌握空间向量的数量积定义.
2.能应用数量积解决简单几何问题.基础梳理1.数量积:a·b=|a||b|cos〈a,b〉不是向量,为实数,其中〈a,b〉为向量的夹角.
例1 a2=a·a=__________,|a|=________;
2.a在b上的射影是指________________.
例2 |a|=6,cos〈a,b〉=- ,则a在b上的射影是______________.
3.两个向量a、b的夹角公式cos θ=____________在空间图形中仍成立.
例3 |a|=3,|b|=2,a·b=-3,则cos〈a,b〉=______.|a|2 |a|cos〈a,b〉 -3 4.空间向量的数量积满足以下运算律:
(1)(λa)·b=____________;
(2)a·b=____________;
(3)a·(b+c)=________________.
5.线线垂直:若a,b是非零向量,则a⊥b?______.
6.两个向量的夹角的范围是:________.4.(1)λ(a·b) (2)b·a (3)a·b+a·c
5.a·b=0
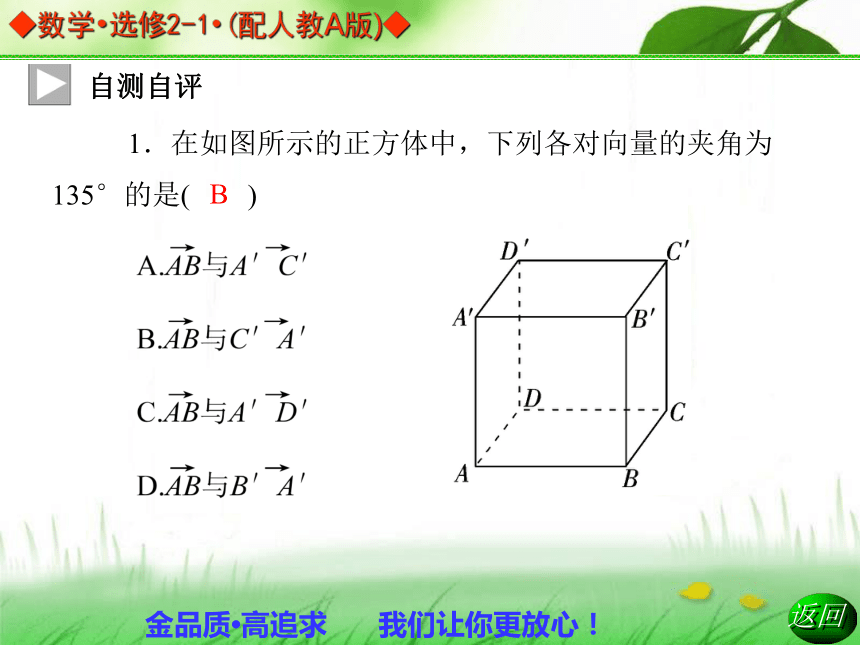
6.[0,π]自测自评1.在如图所示的正方体中,下列各对向量的夹角为135°的是( )B 2.在棱长为1的正方体ABCD—A1B1C1D1中,设 =a, =b, =c,则a·(b+c)的值为( )
A.1 B.0
C.-1 D.-2
3.|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为( )
A.30° B.60°
C.120° D.150°B C 利用数量积求夹角的余弦值 已知点O是正△ABC平面外的一点,若OA=OB=OC=AB=1,E、F分别是AB、OC的中点,试求 与 所成角的余弦值.
解析:如图所示,设 =a, =b, =c,
则a·b=b·c=c·a= ,
|a|=|b|=|c|=1,跟踪训练1.如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求 与 夹角的余弦值.答案:利用数量积求两点间的距离 在正四面体ABCD中,棱长为a,M,N分别是棱AB,CD上的点,且|MB|=2|AM|,|CN|= |ND|,求|MN|.跟踪训练2.把长AB和宽AD分别为2 和2的长方形ABCD沿对角线AC折成60°的二面角,求B、D间的距离.答案:利用数量积证明垂直问题 已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC,M、N分别是OA、BC的中点,G是MN的中点.
求证:OG⊥BC.
证明:连结ON,
设∠AOB=∠BOC=∠AOC=θ,跟踪训练3.已知在空间四边形OABC中,OB=OC,AB=AC,求证:OA⊥BC.一、选择填空题
1.下列式子正确的是( )
A.a·|a|=a B.(a·b)2=a·b
C.(a·b)c=a·(b·c) D.|a·b|≤|a||b|
2.若向量m同时垂直两个向量a和b,向量n=λa+μb(λ,μ∈R,λ,μ≠0)则( )
A.m∥n
B.m⊥n
C.m与n既不平行也不垂直
D.以上三种情况均有可能D B 1.注意向量乘法的结合律是不成立的,即a·(b·c)= (a·b)·c是不成立.事实上a·(b·c)表示与a平行的向量,而(a·b)·c表示与c平行的向量.
2.两个非零向量共线时,如果同向,夹角为0,如果异向,夹角为π,特别的〈a,a〉=0,〈a,-a〉=π.
3.注意二个向量夹角的范围:[0,π],当夹角为锐角时其余弦值为正,当夹角为钝角时其余弦值为负.反之当两向量不共线时亦成立.祝您学业有成
3.1.3 空间向量的数量积运算空间向量与立体几何 1.掌握空间向量的数量积定义.
2.能应用数量积解决简单几何问题.基础梳理1.数量积:a·b=|a||b|cos〈a,b〉不是向量,为实数,其中〈a,b〉为向量的夹角.
例1 a2=a·a=__________,|a|=________;
2.a在b上的射影是指________________.
例2 |a|=6,cos〈a,b〉=- ,则a在b上的射影是______________.
3.两个向量a、b的夹角公式cos θ=____________在空间图形中仍成立.
例3 |a|=3,|b|=2,a·b=-3,则cos〈a,b〉=______.|a|2 |a|cos〈a,b〉 -3 4.空间向量的数量积满足以下运算律:
(1)(λa)·b=____________;
(2)a·b=____________;
(3)a·(b+c)=________________.
5.线线垂直:若a,b是非零向量,则a⊥b?______.
6.两个向量的夹角的范围是:________.4.(1)λ(a·b) (2)b·a (3)a·b+a·c
5.a·b=0
6.[0,π]自测自评1.在如图所示的正方体中,下列各对向量的夹角为135°的是( )B 2.在棱长为1的正方体ABCD—A1B1C1D1中,设 =a, =b, =c,则a·(b+c)的值为( )
A.1 B.0
C.-1 D.-2
3.|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为( )
A.30° B.60°
C.120° D.150°B C 利用数量积求夹角的余弦值 已知点O是正△ABC平面外的一点,若OA=OB=OC=AB=1,E、F分别是AB、OC的中点,试求 与 所成角的余弦值.
解析:如图所示,设 =a, =b, =c,
则a·b=b·c=c·a= ,
|a|=|b|=|c|=1,跟踪训练1.如图,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,求 与 夹角的余弦值.答案:利用数量积求两点间的距离 在正四面体ABCD中,棱长为a,M,N分别是棱AB,CD上的点,且|MB|=2|AM|,|CN|= |ND|,求|MN|.跟踪训练2.把长AB和宽AD分别为2 和2的长方形ABCD沿对角线AC折成60°的二面角,求B、D间的距离.答案:利用数量积证明垂直问题 已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC,M、N分别是OA、BC的中点,G是MN的中点.
求证:OG⊥BC.
证明:连结ON,
设∠AOB=∠BOC=∠AOC=θ,跟踪训练3.已知在空间四边形OABC中,OB=OC,AB=AC,求证:OA⊥BC.一、选择填空题
1.下列式子正确的是( )
A.a·|a|=a B.(a·b)2=a·b
C.(a·b)c=a·(b·c) D.|a·b|≤|a||b|
2.若向量m同时垂直两个向量a和b,向量n=λa+μb(λ,μ∈R,λ,μ≠0)则( )
A.m∥n
B.m⊥n
C.m与n既不平行也不垂直
D.以上三种情况均有可能D B 1.注意向量乘法的结合律是不成立的,即a·(b·c)= (a·b)·c是不成立.事实上a·(b·c)表示与a平行的向量,而(a·b)·c表示与c平行的向量.
2.两个非零向量共线时,如果同向,夹角为0,如果异向,夹角为π,特别的〈a,a〉=0,〈a,-a〉=π.
3.注意二个向量夹角的范围:[0,π],当夹角为锐角时其余弦值为正,当夹角为钝角时其余弦值为负.反之当两向量不共线时亦成立.祝您学业有成
