2013-2014学年高中数学人教A版选修2-1同步辅导与检测:3.2.3利用空间向量求角
文档属性
| 名称 | 2013-2014学年高中数学人教A版选修2-1同步辅导与检测:3.2.3利用空间向量求角 |

|
|
| 格式 | zip | ||
| 文件大小 | 638.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-05 00:00:00 | ||
图片预览








文档简介
课件27张PPT。3.2 立体几何中的向量方法
3.2.3 利用空间向量求角 空间向量与立体几何 1.认识空间角的含义,主要是:两异面直线所成角、二面角、线面角.
2.明确利用向量求各种角的方法.基础梳理1.相交直线的夹角:两条直线相交所成的__________.
异面直线的角:与这两条异面直线分别平行的两相交直线所成的______.
2.夹角的范围都是____________.
3.直线与平面平行或在平面内时:直线与平面所成角为______;
直线与平面垂直时: 直线与平面所成角为________;
斜线与平面所成角: 直线与平面所成角范围为____________.1.锐角或直角 夹角 2.0°<θ≤90°
3.0° 90° 0°<θ<90°4.两平面的法向量分别为:a,b,则两平面所成二面角________________.
5.两个平面所成二面角为θ,则θ范围为________.4.等于这两条法向量所成角或与两法向量所成角互补
5.0<θ≤π自测自评1.设n1,n2分别为一个二面角的两个半平面的法向量,若〈n1,n2〉= π,则此二面角的大小为________________.
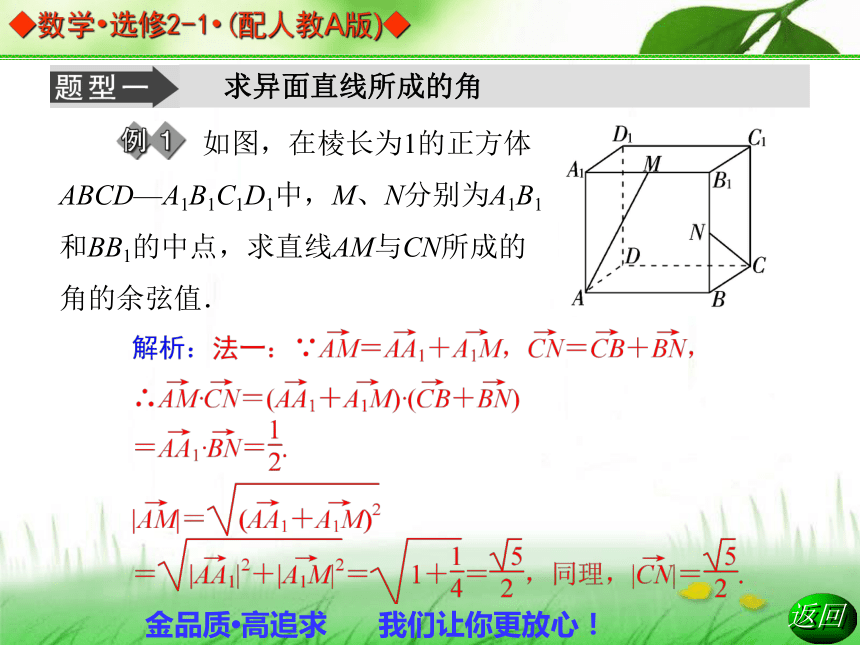
2.正方体AC1中,BD1与AA1所成角的余弦为( )A D 求异面直线所成的角 如图,在棱长为1的正方体ABCD—A1B1C1D1中,M、N分别为A1B1和BB1的中点,求直线AM与CN所成的角的余弦值.跟踪训练1.已知平行六面体ABCD—A1B1C1D1的所有棱长都是1,且∠A1AB=∠A1AD=∠BAD=60°,求直线AC1与AC所成角的余弦值.答案:求直线与平面所成的角 在边长为1的正方体ABCD—A1B1C1D1中,E和F分别是BC和C1D1上的点,BE=C1F= ,试求EF与平面A1BD所成的角的正弦值. 解析:以A为原点,分别以 , , 方向为x轴,y轴,z轴的正方向建立坐标系,如下图所示, 则A1(0,0,1),B(1,0,0),D(0,1,0),C1(1,1,1,),跟踪训练2.正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为 a,求AC1与侧面AA1B1B所成的角.求二面角的平面角 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知PD= , CD=2 ,AE= ,求二面角E-PC-D的大小.解析:以D为原点, 分别为x,y,z轴的正方向建立空间直角坐标系如右图所示.
由已知可得D(0,0,0),P(0,0,),C(0,2,0)跟踪训练3.如图在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.设AA1=AC= AB,求二面角A1-AD-C1的大小.解析:如图建立空间直角坐标系O-xyz,其中原点O不AC的中点.
不妨设A(1,0,0),则B(0,1,0),C(-1,0,0),A1(1,0,2),一、选择填空题
1.已知线段AB的两个端点的坐标分别为A(9,-3,4)和B(9,2,1),则线段AB( )
A.与平面xOy平行
B.与平面xOz平行
C.与平面zOy平行
D.与平面xOy或zOy平行
2.已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=3,AB=2,BC= ,则二面角P-BD-A的正切值为________.C 1.用向量法求二面角,在正确建立直角坐标系的前题下,求二面角二个面的法向量是关键,正确列出方程组求解;并且要正确判断所求角是二面角的平面角还是其补角.
2.求异面直线所成的角主要是转化为两个向量的夹角,这时要特别注意二向量的方向及最后求出的角一定要是锐角或直角.
3.线面角是求线与平面的法向量所成角的余角.祝您学业有成
3.2.3 利用空间向量求角 空间向量与立体几何 1.认识空间角的含义,主要是:两异面直线所成角、二面角、线面角.
2.明确利用向量求各种角的方法.基础梳理1.相交直线的夹角:两条直线相交所成的__________.
异面直线的角:与这两条异面直线分别平行的两相交直线所成的______.
2.夹角的范围都是____________.
3.直线与平面平行或在平面内时:直线与平面所成角为______;
直线与平面垂直时: 直线与平面所成角为________;
斜线与平面所成角: 直线与平面所成角范围为____________.1.锐角或直角 夹角 2.0°<θ≤90°
3.0° 90° 0°<θ<90°4.两平面的法向量分别为:a,b,则两平面所成二面角________________.
5.两个平面所成二面角为θ,则θ范围为________.4.等于这两条法向量所成角或与两法向量所成角互补
5.0<θ≤π自测自评1.设n1,n2分别为一个二面角的两个半平面的法向量,若〈n1,n2〉= π,则此二面角的大小为________________.
2.正方体AC1中,BD1与AA1所成角的余弦为( )A D 求异面直线所成的角 如图,在棱长为1的正方体ABCD—A1B1C1D1中,M、N分别为A1B1和BB1的中点,求直线AM与CN所成的角的余弦值.跟踪训练1.已知平行六面体ABCD—A1B1C1D1的所有棱长都是1,且∠A1AB=∠A1AD=∠BAD=60°,求直线AC1与AC所成角的余弦值.答案:求直线与平面所成的角 在边长为1的正方体ABCD—A1B1C1D1中,E和F分别是BC和C1D1上的点,BE=C1F= ,试求EF与平面A1BD所成的角的正弦值. 解析:以A为原点,分别以 , , 方向为x轴,y轴,z轴的正方向建立坐标系,如下图所示, 则A1(0,0,1),B(1,0,0),D(0,1,0),C1(1,1,1,),跟踪训练2.正三棱柱ABC-A1B1C1的底面边长为a,侧棱长为 a,求AC1与侧面AA1B1B所成的角.求二面角的平面角 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC. 已知PD= , CD=2 ,AE= ,求二面角E-PC-D的大小.解析:以D为原点, 分别为x,y,z轴的正方向建立空间直角坐标系如右图所示.
由已知可得D(0,0,0),P(0,0,),C(0,2,0)跟踪训练3.如图在直三棱柱ABC-A1B1C1中,AB=BC,D、E分别为BB1、AC1的中点.设AA1=AC= AB,求二面角A1-AD-C1的大小.解析:如图建立空间直角坐标系O-xyz,其中原点O不AC的中点.
不妨设A(1,0,0),则B(0,1,0),C(-1,0,0),A1(1,0,2),一、选择填空题
1.已知线段AB的两个端点的坐标分别为A(9,-3,4)和B(9,2,1),则线段AB( )
A.与平面xOy平行
B.与平面xOz平行
C.与平面zOy平行
D.与平面xOy或zOy平行
2.已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=3,AB=2,BC= ,则二面角P-BD-A的正切值为________.C 1.用向量法求二面角,在正确建立直角坐标系的前题下,求二面角二个面的法向量是关键,正确列出方程组求解;并且要正确判断所求角是二面角的平面角还是其补角.
2.求异面直线所成的角主要是转化为两个向量的夹角,这时要特别注意二向量的方向及最后求出的角一定要是锐角或直角.
3.线面角是求线与平面的法向量所成角的余角.祝您学业有成
