2013-2014学年高中数学苏教版必修2同步辅导与检测:1.1.4直观图画法
文档属性
| 名称 | 2013-2014学年高中数学苏教版必修2同步辅导与检测:1.1.4直观图画法 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 00:00:00 | ||
图片预览











文档简介
课件32张PPT。立体几何初步 1.1 空间几何体
1.1.4 直观图画法如下图所示的建筑物是江南著名古镇之一的乌镇,它是由不同的几何体组合而成的,建筑工人在建造时要依据工程设计的图纸进行施工,工程师是利用什么方法画出图纸呢?1.____________________叫做空间图形的直观图.
2.斜二测画法是一种画直观图的方法,是一种特殊的平行投影画法,其步骤为:①在已知图形中取互相垂直的x轴和y轴,两轴相交于点O,画直观图时,把它们画成对应的x'轴和y'轴,两轴相交于点O',且使∠x'O'y'=________,它们确定的平面表示水平面;②已知图形中平行于x轴或y轴的线段,在直观图中分别画成______或______的线段;③已知图形中________的线段,在直观图中保持原长度不变,________的线段,长度变为原来的一半.1.表示空间图形的平面图形
2.45°或135° 平行于x'轴 y'轴 平行于x轴
平行 于y轴3.画水平放置图形的步骤:①在水平放置的图形中建适当的直角坐标系x-O-y,使图形中的点尽可能地在________;②画出直观图中的坐标系x'-O'-y',使∠x'O'y'=________;③在原图中取关键点,得到____________线段;④按照画法规则,____________,在直观图的坐标系中取出相应的点,得到相应的直观图.坐标轴上或关于坐标轴对称 45°或135° 在坐标轴上或与坐标轴平行的 平行于x轴的线段长度不变,与y轴平行的减半4.画空间几何直观图的步骤:①取相互垂直的Ox、Oy轴,再取Oz轴,使______________;②画O'x'、O 'y'、O'z',使____________________;③画底面:平行于x轴的线段在直观图中长度________,平行于y轴的线段在直观图中长度________;④画侧棱(或高):平行于z轴的线段在直观图中长度________;⑤成图:顺次连接各个线段的端点,构成直观图(注意实线与虚线).∠xOz=90°且∠yOz=90° ∠x'O'y'=45°(或135°),∠x'O'z'=90° 不变 减半 不变用斜二测画法画水平放置图形的步骤1.在水平放置的图形中建适当的直角坐标系x-O-y,使图形中的点尽可能地在坐标轴上或关于坐标轴对称;
2.画出直观图中的坐标系x‘-O’-y‘,使∠x’O‘y’=45°或135°;
3.在原图中取关键点,得到在坐标轴上或与坐标轴平行的线段;
4.按照画法规则,平行性不变,长度与y轴平行的减半,在直观图的坐标系中取出相应的点,得到相应的直观图.用斜二测画法画空间几何体直观图的步骤1.取互相垂直的Ox、Oy轴,再取Oz轴,使∠xOz=90°;且∠yOz=90°;
2.画O'x'、O'y'、O'z',使∠x'O'y'=45°(或135°),∠x'O'z'=90°;
3.画底面:平行于x轴的线段在直观图中长度不变,平行于y轴的线段在直观图中长度减半;
4.画侧棱(或高):平行于z轴的线段在直观图中保持长度不变;
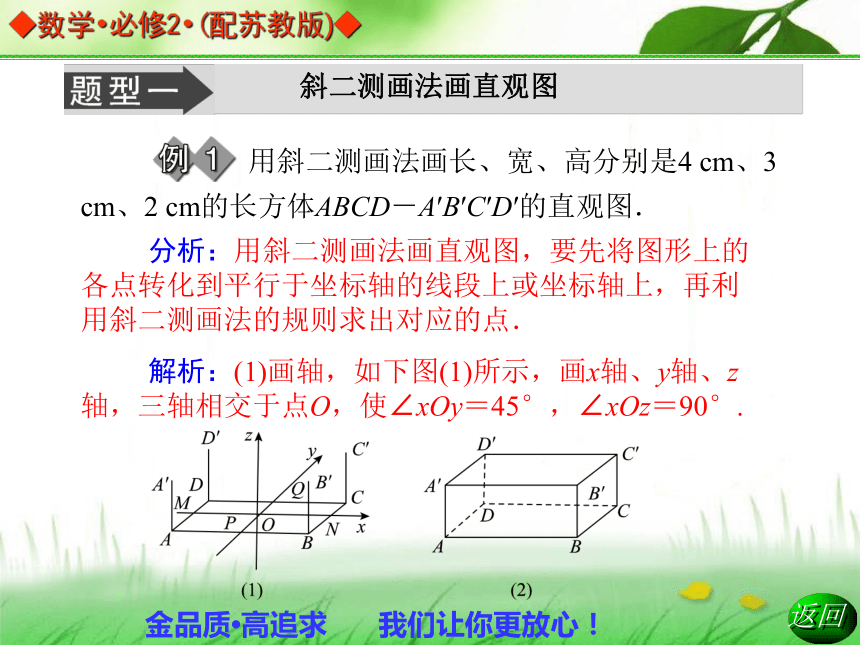
5.成图:顺次连接各个线段的端点,构成直观图(注意实线与虚线).斜二测画法画直观图 用斜二测画法画长、宽、高分别是4 cm、3 cm、2 cm的长方体ABCD-A′B′C′D′的直观图. 分析:用斜二测画法画直观图,要先将图形上的各点转化到平行于坐标轴的线段上或坐标轴上,再利用斜二测画法的规则求出对应的点.
解析:(1)画轴,如下图(1)所示,画x轴、y轴、z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.(2)画底面,以点O为中点,在x轴上取线段MN,使MN=4 cm;在y轴上取线段PQ,使PQ= cm,分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A、B、C、D,四边形ABCD就是长方体的底面ABCD.
(3)画侧棱,过A、B、C、D各取分别作z轴的平行线,并在这些平行线上分别截取2 cm长的线段AA′、BB′、CC′、DD′.
(4)成图,顺次连接A′、B′、C′、D′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图如上图(2).规律总结:(1)用斜二测画法作空间图形(立体图形)的直观图,原图形的高在直观图中不变.
(2)不同的选取方法意味着解题的难易,为了保证画图既快又准,应充分注意以下两点:
①充分利用图形的对称性;②尽可能让更多的顶点在坐标轴上.
在应用斜二测画法画直观图时,首先要观察分析,选取恰当的坐标系,再应用斜二测画法画直观图.变式训练1.用斜二测画法画水平放置的边长为12厘米、15厘米、21厘米的三角形的直观图.分析:首先应先建立坐标系,可以以点B为坐标原点,线段BC所在直线为x轴,再用斜二测画法画水平放置的三角形的直观图.
解析:步骤:(1)在已知图形中取直线BC为x轴,垂直BC的直线为y轴,两轴相交于点B,如下图(1),画对应的x′轴和y′轴,两轴交于点D,使∠x'Dy′=45°,如下图(2).(2)过点A作BC的垂线,垂足为G,在x′轴上截取DH=BG,截取DE=BC,过H作直线HF平行于y′轴,在直线HF上截取线段HF等于线段AG的一半.
(3)连接DF、EF,△FDE即为水平放置的△ABC的直观图.由三视图画直观图 根据下图的三视图想象物体原形,并画出物体的实物草图.分析:由常见几何体的三视图及三视图的画法,再画实物图.
解析:(1)由俯视图并结合其他两个视图可以看出,这个物体是由一个圆柱和一个正四棱柱组合而成,圆柱的下底面圆和正四棱柱的上底面正方形内切,它的实物草图如下图(1).
(2)由三视图知,该物体下部分是一个长方体,上部分的表面是两个等腰梯形和两个等腰三角形,它的实物草图如下图(2).规律总结:由三视图想象几何体的实物图,要分清组合体中每一部分是什么几何体,三视图在机械制造、工程建设中起到主要作用.变式训练2.画出一个正三棱台的直观图(尺寸为:上、下底面边长为1 cm、2 cm,高1 cm). (1)画轴:如下图,画x轴、y轴、z轴三轴相交于O,使∠xOy=45°,∠xOz=90°.
(2)画下底面:在y轴的负半轴上取一点D,使OD= cm,过D作x轴的平行线AB,使AB=2 cm,在y轴的正半轴上取一点C使OC= cm.连接BC、CA,则△ABC为正三棱台的下底面.
(3)画上底面:在z轴上取线段OO′,使OO′=1 cm,过O′点作O'x'∥Ox,O'y'∥Oy.建立坐标系x'O'y',在x'O'y′中,重复(2)的步骤,使A′B′=1 cm,得上底面A′B′C′.
(4)连线成图:连接AA′、BB′、CC′,则三棱台ABC-A′B′C′为要求的三棱台的直观图.由直观图还原实际图形 下图(1)为一个平面图形的直观图,请画出它的实际形状.分析:先建立45°角的坐标系,再建立直角坐标系,然后还原成实际图形.
解析:建立如下图(1)所示的坐标系x'A'y',再建立一个直角坐标系,如下图(2)所示.在x轴上截取线段AB=A′B′,在y轴上截取线段AD,使AD=2A′D′.
过B作BC∥AD,过D作DC∥AB,使BC与DC交于点C,则四边形ABCD为A′B′C′D′的实际图形.
规律总结:将水平放置的平面图形的直观图还原成原来的实际图形,其作法就是逆用斜二测画法,也就是使平行于x轴的线段长度不变,而平行于y轴的线段长度为原来的2倍.变式训练3.如右图,△A′B′C′是水平放置的平面图形的斜二测直观图,将其恢复成原图形.过B′作B′D′∥y′轴交O′A′于D′,取直角坐标系xOy;选取OA=O′A′,OD=O′D′,作DB∥y轴,且DB=2D′B′,连接BO、BA,则△BOA即为原图形.如右图所示.水平面放置的平面图形的面积 已知正三角形ABC的边长为a,那么△ABC的平面直观图△A′B′C′的面积为________.解析:先根据题意,画出直观图,然后根据直观图
△A′B′C′的边长及夹角求解.规律总结:求直观图的面积的关键是依据斜二测画法,求出相应的直观图的底边和高,也就是原来实际图形中的高线,在直观图中变为与水平直线成45°角且长度为原来的一半的线段,以此为依据来求出相应的高线即可.变式训练4.对于一个底边在x轴上的正三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的________倍.直观图的斜二测画法1.利用斜二测画法得到的:
①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形.以上结论,正确的是________.解析:因平行性不改变,故②正确,①也正确;平行于y轴的线段,长度变为原来的一半,故③、④不正确.
答案:①②能力升级平面图形、空间几何体的直观图的画法7.画出水平放置的等腰梯形的直观图.画法:
(1)如图(1),取AB所在直线为x轴,AB的中点O为原点,AB的中垂线为y轴建立直角坐标系,画出对应的直观图中的坐标系O'x'y',使∠x'O'y'=45°(或135°);
(2)以O′为中点在x′轴上取A′B′=AB,在y′轴上取O′E′= OE,以E′为中点画C′D′∥x′轴并使C′D′=CD;(3)连接B′C′、D′A′,如图(2),所得到的四边形A′B′C′D′即是水平放置的等腰梯形ABCD的直观图.祝您学业有成
1.1.4 直观图画法如下图所示的建筑物是江南著名古镇之一的乌镇,它是由不同的几何体组合而成的,建筑工人在建造时要依据工程设计的图纸进行施工,工程师是利用什么方法画出图纸呢?1.____________________叫做空间图形的直观图.
2.斜二测画法是一种画直观图的方法,是一种特殊的平行投影画法,其步骤为:①在已知图形中取互相垂直的x轴和y轴,两轴相交于点O,画直观图时,把它们画成对应的x'轴和y'轴,两轴相交于点O',且使∠x'O'y'=________,它们确定的平面表示水平面;②已知图形中平行于x轴或y轴的线段,在直观图中分别画成______或______的线段;③已知图形中________的线段,在直观图中保持原长度不变,________的线段,长度变为原来的一半.1.表示空间图形的平面图形
2.45°或135° 平行于x'轴 y'轴 平行于x轴
平行 于y轴3.画水平放置图形的步骤:①在水平放置的图形中建适当的直角坐标系x-O-y,使图形中的点尽可能地在________;②画出直观图中的坐标系x'-O'-y',使∠x'O'y'=________;③在原图中取关键点,得到____________线段;④按照画法规则,____________,在直观图的坐标系中取出相应的点,得到相应的直观图.坐标轴上或关于坐标轴对称 45°或135° 在坐标轴上或与坐标轴平行的 平行于x轴的线段长度不变,与y轴平行的减半4.画空间几何直观图的步骤:①取相互垂直的Ox、Oy轴,再取Oz轴,使______________;②画O'x'、O 'y'、O'z',使____________________;③画底面:平行于x轴的线段在直观图中长度________,平行于y轴的线段在直观图中长度________;④画侧棱(或高):平行于z轴的线段在直观图中长度________;⑤成图:顺次连接各个线段的端点,构成直观图(注意实线与虚线).∠xOz=90°且∠yOz=90° ∠x'O'y'=45°(或135°),∠x'O'z'=90° 不变 减半 不变用斜二测画法画水平放置图形的步骤1.在水平放置的图形中建适当的直角坐标系x-O-y,使图形中的点尽可能地在坐标轴上或关于坐标轴对称;
2.画出直观图中的坐标系x‘-O’-y‘,使∠x’O‘y’=45°或135°;
3.在原图中取关键点,得到在坐标轴上或与坐标轴平行的线段;
4.按照画法规则,平行性不变,长度与y轴平行的减半,在直观图的坐标系中取出相应的点,得到相应的直观图.用斜二测画法画空间几何体直观图的步骤1.取互相垂直的Ox、Oy轴,再取Oz轴,使∠xOz=90°;且∠yOz=90°;
2.画O'x'、O'y'、O'z',使∠x'O'y'=45°(或135°),∠x'O'z'=90°;
3.画底面:平行于x轴的线段在直观图中长度不变,平行于y轴的线段在直观图中长度减半;
4.画侧棱(或高):平行于z轴的线段在直观图中保持长度不变;
5.成图:顺次连接各个线段的端点,构成直观图(注意实线与虚线).斜二测画法画直观图 用斜二测画法画长、宽、高分别是4 cm、3 cm、2 cm的长方体ABCD-A′B′C′D′的直观图. 分析:用斜二测画法画直观图,要先将图形上的各点转化到平行于坐标轴的线段上或坐标轴上,再利用斜二测画法的规则求出对应的点.
解析:(1)画轴,如下图(1)所示,画x轴、y轴、z轴,三轴相交于点O,使∠xOy=45°,∠xOz=90°.(2)画底面,以点O为中点,在x轴上取线段MN,使MN=4 cm;在y轴上取线段PQ,使PQ= cm,分别过点M和N作y轴的平行线,过点P和Q作x轴的平行线,设它们的交点分别为A、B、C、D,四边形ABCD就是长方体的底面ABCD.
(3)画侧棱,过A、B、C、D各取分别作z轴的平行线,并在这些平行线上分别截取2 cm长的线段AA′、BB′、CC′、DD′.
(4)成图,顺次连接A′、B′、C′、D′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到长方体的直观图如上图(2).规律总结:(1)用斜二测画法作空间图形(立体图形)的直观图,原图形的高在直观图中不变.
(2)不同的选取方法意味着解题的难易,为了保证画图既快又准,应充分注意以下两点:
①充分利用图形的对称性;②尽可能让更多的顶点在坐标轴上.
在应用斜二测画法画直观图时,首先要观察分析,选取恰当的坐标系,再应用斜二测画法画直观图.变式训练1.用斜二测画法画水平放置的边长为12厘米、15厘米、21厘米的三角形的直观图.分析:首先应先建立坐标系,可以以点B为坐标原点,线段BC所在直线为x轴,再用斜二测画法画水平放置的三角形的直观图.
解析:步骤:(1)在已知图形中取直线BC为x轴,垂直BC的直线为y轴,两轴相交于点B,如下图(1),画对应的x′轴和y′轴,两轴交于点D,使∠x'Dy′=45°,如下图(2).(2)过点A作BC的垂线,垂足为G,在x′轴上截取DH=BG,截取DE=BC,过H作直线HF平行于y′轴,在直线HF上截取线段HF等于线段AG的一半.
(3)连接DF、EF,△FDE即为水平放置的△ABC的直观图.由三视图画直观图 根据下图的三视图想象物体原形,并画出物体的实物草图.分析:由常见几何体的三视图及三视图的画法,再画实物图.
解析:(1)由俯视图并结合其他两个视图可以看出,这个物体是由一个圆柱和一个正四棱柱组合而成,圆柱的下底面圆和正四棱柱的上底面正方形内切,它的实物草图如下图(1).
(2)由三视图知,该物体下部分是一个长方体,上部分的表面是两个等腰梯形和两个等腰三角形,它的实物草图如下图(2).规律总结:由三视图想象几何体的实物图,要分清组合体中每一部分是什么几何体,三视图在机械制造、工程建设中起到主要作用.变式训练2.画出一个正三棱台的直观图(尺寸为:上、下底面边长为1 cm、2 cm,高1 cm). (1)画轴:如下图,画x轴、y轴、z轴三轴相交于O,使∠xOy=45°,∠xOz=90°.
(2)画下底面:在y轴的负半轴上取一点D,使OD= cm,过D作x轴的平行线AB,使AB=2 cm,在y轴的正半轴上取一点C使OC= cm.连接BC、CA,则△ABC为正三棱台的下底面.
(3)画上底面:在z轴上取线段OO′,使OO′=1 cm,过O′点作O'x'∥Ox,O'y'∥Oy.建立坐标系x'O'y',在x'O'y′中,重复(2)的步骤,使A′B′=1 cm,得上底面A′B′C′.
(4)连线成图:连接AA′、BB′、CC′,则三棱台ABC-A′B′C′为要求的三棱台的直观图.由直观图还原实际图形 下图(1)为一个平面图形的直观图,请画出它的实际形状.分析:先建立45°角的坐标系,再建立直角坐标系,然后还原成实际图形.
解析:建立如下图(1)所示的坐标系x'A'y',再建立一个直角坐标系,如下图(2)所示.在x轴上截取线段AB=A′B′,在y轴上截取线段AD,使AD=2A′D′.
过B作BC∥AD,过D作DC∥AB,使BC与DC交于点C,则四边形ABCD为A′B′C′D′的实际图形.
规律总结:将水平放置的平面图形的直观图还原成原来的实际图形,其作法就是逆用斜二测画法,也就是使平行于x轴的线段长度不变,而平行于y轴的线段长度为原来的2倍.变式训练3.如右图,△A′B′C′是水平放置的平面图形的斜二测直观图,将其恢复成原图形.过B′作B′D′∥y′轴交O′A′于D′,取直角坐标系xOy;选取OA=O′A′,OD=O′D′,作DB∥y轴,且DB=2D′B′,连接BO、BA,则△BOA即为原图形.如右图所示.水平面放置的平面图形的面积 已知正三角形ABC的边长为a,那么△ABC的平面直观图△A′B′C′的面积为________.解析:先根据题意,画出直观图,然后根据直观图
△A′B′C′的边长及夹角求解.规律总结:求直观图的面积的关键是依据斜二测画法,求出相应的直观图的底边和高,也就是原来实际图形中的高线,在直观图中变为与水平直线成45°角且长度为原来的一半的线段,以此为依据来求出相应的高线即可.变式训练4.对于一个底边在x轴上的正三角形,采用斜二测画法作出其直观图,其直观图面积是原三角形面积的________倍.直观图的斜二测画法1.利用斜二测画法得到的:
①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形.以上结论,正确的是________.解析:因平行性不改变,故②正确,①也正确;平行于y轴的线段,长度变为原来的一半,故③、④不正确.
答案:①②能力升级平面图形、空间几何体的直观图的画法7.画出水平放置的等腰梯形的直观图.画法:
(1)如图(1),取AB所在直线为x轴,AB的中点O为原点,AB的中垂线为y轴建立直角坐标系,画出对应的直观图中的坐标系O'x'y',使∠x'O'y'=45°(或135°);
(2)以O′为中点在x′轴上取A′B′=AB,在y′轴上取O′E′= OE,以E′为中点画C′D′∥x′轴并使C′D′=CD;(3)连接B′C′、D′A′,如图(2),所得到的四边形A′B′C′D′即是水平放置的等腰梯形ABCD的直观图.祝您学业有成
