2013-2014学年高中数学苏教版必修2同步辅导与检测:2.1.3两条直线的平行与垂直
文档属性
| 名称 | 2013-2014学年高中数学苏教版必修2同步辅导与检测:2.1.3两条直线的平行与垂直 |

|
|
| 格式 | zip | ||
| 文件大小 | 789.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 20:41:57 | ||
图片预览











文档简介
课件34张PPT。2.1 直线与方程
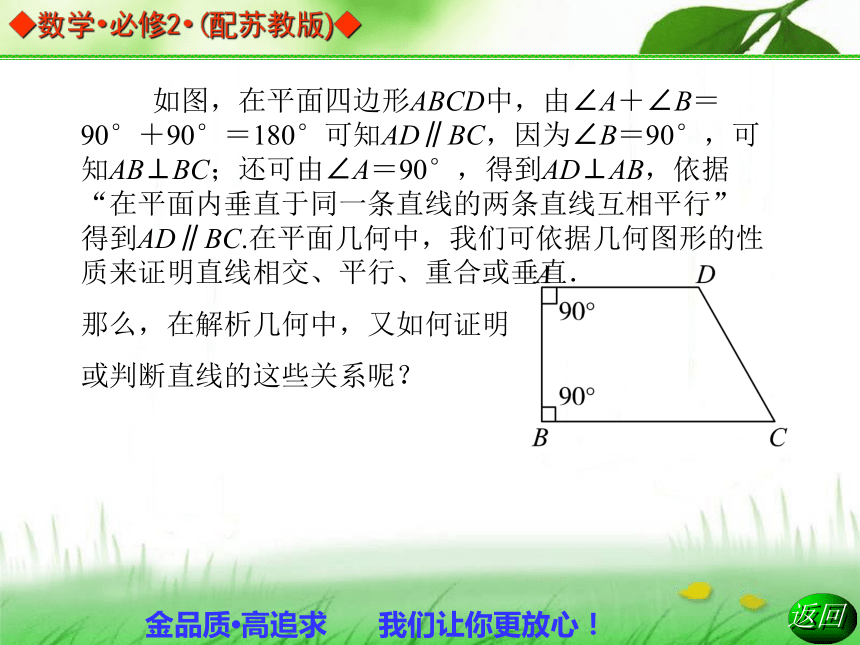
2.1.3 两条直线的平行与垂直 平面解析几何初步 如图,在平面四边形ABCD中,由∠A+∠B=90°+90°=180°可知AD∥BC,因为∠B=90°,可知AB⊥BC;还可由∠A=90°,得到AD⊥AB,依据“在平面内垂直于同一条直线的两条直线互相平行”得到AD∥BC.在平面几何中,我们可依据几何图形的性质来证明直线相交、平行、重合或垂直.
那么,在解析几何中,又如何证明
或判断直线的这些关系呢?1.通过初中的学习我们知道“两直线平行,则两直线的倾斜角相等”,同样,两条直线平行,如果它们的_____,则它们的______.反之也成立,即:已知直线l1:y=k1x+b1;l2:y=k2x+b2,则l1∥l2?______,且b1≠b2.这个结论成立的前提是两条直线______.特别,若两不重合直线的斜率不存在,由于它们的倾斜角都是_____,所以它们______.
2.当直线l1,l2都垂直于x轴且不重合时,由于垂直于同一条直线的两条直线平行,可推得:__________,因此,两条不重合直线平行的判定的一般结论是:l1和l2的斜率都__________或__________且b1≠b2.1.斜率都存在 斜率相等 k1=k2 不重合并且斜率都存在 90° 互相平行
2.l1∥l2 不存在 k1=k23.两直线的斜率都存在时,若两直线垂直,则它们的斜率k1,k2的乘积k1k2=______,反之也成立,即:l1⊥l2 ?k1k2=-1,特别,若两直线中一条直线的斜率为零,另一条直线的斜率不存在,则这两直线一定________.
4.两条直线l1,l2,若一条直线的斜率不存在,同时另一条斜率为0,则两条直线__________.这样,两条直线垂直的判定的一般结论就是:一条直线的斜率__________,同时另一条斜率为__________或k1k2=__________.3.-1 互相垂直
4.垂直 不存在 0 -1两条直线平行与垂直的判定设两条不重合的直线l1,l2的斜率分别为k1,k2,则
①两条直线平行的条件为:l1∥l2?k1=k2且b1≠b2;
②两条直线垂直的条件为:l1⊥l2?k1k2=-1;
③两条直线l1与l2重合?k1=k2且b1=b2.
以上给出了已知直线的斜截式方程条件下判定两条直线位置关系的又一常用方法.判断方法仅适用于两条直线都有斜率的直线.同学们要特别谨记:同时平行于同一坐标轴的两条直线互相平行,分别平行于两坐标轴的两条直线互相垂直.两直线平行 根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点A(2,1),B(-3,5),l2经过C(3,-3),
D(8,-7);
(2)l1的倾斜角为60°,l2经过M(1, ),N(-2, -2 );
(3)l1平行于y轴,l2经过P(0,-2),Q(0,5);
(4)l1经过E(0,1),F(-2,-1),l2经过G(3,4),H(2,3).分析:根据所给条件求出两直线的斜率,根据斜率是否相等进行判断,要注意斜率不存在及两直线重合的情况.
解析:(1)由题意知,
因为k1=k2且A,B,C,D四点不共线,所以l1∥l2.规律总结:(1)判断两直线的平行,应首先看两直线的斜率是否存在,即先看两点的横坐标是否相等.课本中的条件只有在斜率都存在的情况下才可使用,两点的横坐标相等是特殊情况,应特殊判断.
(2)判断斜率是否相等实际是看倾斜角是否相等,归根结底是充分利用两直线平行的条件:同位角相等,则两直线平行.
(3)在两直线斜率都存在且相等的情况下,应注意两直线是否重合(如第(4)题).变式训练1.判断下列各小题中的直线l1与l2是否平行:
(1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1);
(2)l1的斜率为1,l2经过点A(1,1),B(2,2);
(3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3), N(2,0);
(4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5).解析:两直线垂直 已知直线l1经过点A(3,a),B(a-1,2),直线l2经过点C(1,2),D(-2,a+2).
(1)若l1∥l2,求a的值;
(2)若l1⊥l2,求a的值.分析:两直线斜率都存在,则l1∥l2?k1=k2,l1⊥l2?k1k2=-1.据题目所给条件表示出k1,k2,进而求出a的值.规律总结:由C,D两点的横坐标可知l2的斜率一定存在,由A,B两点的横坐标可知l1的斜率可能存在也可能不存在,因此应注意a的取值范围的讨论.
(1)由l1∥l2比较k1,k2时,应首先考虑斜率是否存在.当k1=k2时,还应排除两直线重合的情况.
(2)由l1⊥l2比较k2,k1时,既要考虑斜率是否存在,又要考虑斜率是否为0.变式训练2.判断下列各题中直线l1与l2是否垂直.
(1)l1经过点A(-1,-2),B(1,2),l2经过点M (-2,-1),N(2,1);
(2)l1的斜率为-10,l2经过点A(10,2),B(20,3);
(3)l1经过点A(3,4),B(3,10),l2经过点M(-10,40),N(10,40).平行与垂直的综合运用 已知四边形ABCD的顶点为A(2,2+2), B(-2,2),C(0,2-2),D(4,2),求证四边形ABCD为矩形.分析:证明四边形为矩形有两种方法,一是首先证明四边形是平行四边形,再证明有一对邻边互相垂直;二是直接证明四组邻边都互相垂直.规律总结:(1)很多时候我们都可以结合平行和垂直的充要条件确定多边形的形状,也可以由多边形的形状得到斜率之间的关系,最终求得多边形各顶点坐标.
(2)利用斜率判断三角形及四边形形状,首先要由各顶点坐标求出各边所在直线的斜率,再由斜率判断边与边的关系进而确定四边形形状. 已知直线l的方程为3x+4y-12=0,求直线l′的方程使
(1)l′与l平行,且过点(-1,3);
(2)l′与l垂直,且l′与两坐标轴围成的三角形面积为4.分析:利用一般式下两直线平行与垂直的条件,求解出未知直线的斜率,然后根据所给条件求出直线的方程.规律总结:(1)一般地,直线Ax+By+C=0中系数A,B确定直线的斜率,因此,与直线Ax+By+C=0平行的直线可设为Ax+By+m=0,这是常采用的解题技巧.我们称Ax+By+m=0是与直线Ax+By+C=0平行的直线系方程,参数m可以取m≠C的任意实数,这样就得到无数条与直线Ax+By+C=0平行的平行线系.当m=C时,Ax+By+m=0与Ax+By+C=0重合.
(2)一般地,经过点A(x0,y0),且与直线Ax+By+C=0平行的直线方程为A(x-x0)+B(y-y0)=0.(3)类似地有:与直线Ax+By+C=0垂直的直线系方程为Bx-Ay+m=0(A,B不同时为零).
(4)求解有关直线与坐标轴围成的三角形面积问题,我们可以设直线的截距式方程,直接利用截距写出三角形的面积,也可以利用设直线的其他形式的方程,求解出与坐标轴的交点坐标,然后写出三角形的面积.变式训练3.已知四边形ABCD的顶点为A(m,n),B(6,1),C(3,3),D(2,5),求m和n的值,使四边形ABCD为直角梯形.基础巩固两条直线平行1.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为__________.能力升级平行与垂直的简单应用9.在直角坐标平面内有两个点A(4,2),B(1,-2),在x轴上有点C,使∠ACB= ,则点C的坐标是__________.祝您学业有成
2.1.3 两条直线的平行与垂直 平面解析几何初步 如图,在平面四边形ABCD中,由∠A+∠B=90°+90°=180°可知AD∥BC,因为∠B=90°,可知AB⊥BC;还可由∠A=90°,得到AD⊥AB,依据“在平面内垂直于同一条直线的两条直线互相平行”得到AD∥BC.在平面几何中,我们可依据几何图形的性质来证明直线相交、平行、重合或垂直.
那么,在解析几何中,又如何证明
或判断直线的这些关系呢?1.通过初中的学习我们知道“两直线平行,则两直线的倾斜角相等”,同样,两条直线平行,如果它们的_____,则它们的______.反之也成立,即:已知直线l1:y=k1x+b1;l2:y=k2x+b2,则l1∥l2?______,且b1≠b2.这个结论成立的前提是两条直线______.特别,若两不重合直线的斜率不存在,由于它们的倾斜角都是_____,所以它们______.
2.当直线l1,l2都垂直于x轴且不重合时,由于垂直于同一条直线的两条直线平行,可推得:__________,因此,两条不重合直线平行的判定的一般结论是:l1和l2的斜率都__________或__________且b1≠b2.1.斜率都存在 斜率相等 k1=k2 不重合并且斜率都存在 90° 互相平行
2.l1∥l2 不存在 k1=k23.两直线的斜率都存在时,若两直线垂直,则它们的斜率k1,k2的乘积k1k2=______,反之也成立,即:l1⊥l2 ?k1k2=-1,特别,若两直线中一条直线的斜率为零,另一条直线的斜率不存在,则这两直线一定________.
4.两条直线l1,l2,若一条直线的斜率不存在,同时另一条斜率为0,则两条直线__________.这样,两条直线垂直的判定的一般结论就是:一条直线的斜率__________,同时另一条斜率为__________或k1k2=__________.3.-1 互相垂直
4.垂直 不存在 0 -1两条直线平行与垂直的判定设两条不重合的直线l1,l2的斜率分别为k1,k2,则
①两条直线平行的条件为:l1∥l2?k1=k2且b1≠b2;
②两条直线垂直的条件为:l1⊥l2?k1k2=-1;
③两条直线l1与l2重合?k1=k2且b1=b2.
以上给出了已知直线的斜截式方程条件下判定两条直线位置关系的又一常用方法.判断方法仅适用于两条直线都有斜率的直线.同学们要特别谨记:同时平行于同一坐标轴的两条直线互相平行,分别平行于两坐标轴的两条直线互相垂直.两直线平行 根据下列给定的条件,判断直线l1与直线l2是否平行.
(1)l1经过点A(2,1),B(-3,5),l2经过C(3,-3),
D(8,-7);
(2)l1的倾斜角为60°,l2经过M(1, ),N(-2, -2 );
(3)l1平行于y轴,l2经过P(0,-2),Q(0,5);
(4)l1经过E(0,1),F(-2,-1),l2经过G(3,4),H(2,3).分析:根据所给条件求出两直线的斜率,根据斜率是否相等进行判断,要注意斜率不存在及两直线重合的情况.
解析:(1)由题意知,
因为k1=k2且A,B,C,D四点不共线,所以l1∥l2.规律总结:(1)判断两直线的平行,应首先看两直线的斜率是否存在,即先看两点的横坐标是否相等.课本中的条件只有在斜率都存在的情况下才可使用,两点的横坐标相等是特殊情况,应特殊判断.
(2)判断斜率是否相等实际是看倾斜角是否相等,归根结底是充分利用两直线平行的条件:同位角相等,则两直线平行.
(3)在两直线斜率都存在且相等的情况下,应注意两直线是否重合(如第(4)题).变式训练1.判断下列各小题中的直线l1与l2是否平行:
(1)l1经过点A(-1,-2),B(2,1),l2经过点M(3,4),N(-1,-1);
(2)l1的斜率为1,l2经过点A(1,1),B(2,2);
(3)l1经过点A(0,1),B(1,0),l2经过点M(-1,3), N(2,0);
(4)l1经过点A(-3,2),B(-3,10),l2经过点M(5,-2),N(5,5).解析:两直线垂直 已知直线l1经过点A(3,a),B(a-1,2),直线l2经过点C(1,2),D(-2,a+2).
(1)若l1∥l2,求a的值;
(2)若l1⊥l2,求a的值.分析:两直线斜率都存在,则l1∥l2?k1=k2,l1⊥l2?k1k2=-1.据题目所给条件表示出k1,k2,进而求出a的值.规律总结:由C,D两点的横坐标可知l2的斜率一定存在,由A,B两点的横坐标可知l1的斜率可能存在也可能不存在,因此应注意a的取值范围的讨论.
(1)由l1∥l2比较k1,k2时,应首先考虑斜率是否存在.当k1=k2时,还应排除两直线重合的情况.
(2)由l1⊥l2比较k2,k1时,既要考虑斜率是否存在,又要考虑斜率是否为0.变式训练2.判断下列各题中直线l1与l2是否垂直.
(1)l1经过点A(-1,-2),B(1,2),l2经过点M (-2,-1),N(2,1);
(2)l1的斜率为-10,l2经过点A(10,2),B(20,3);
(3)l1经过点A(3,4),B(3,10),l2经过点M(-10,40),N(10,40).平行与垂直的综合运用 已知四边形ABCD的顶点为A(2,2+2), B(-2,2),C(0,2-2),D(4,2),求证四边形ABCD为矩形.分析:证明四边形为矩形有两种方法,一是首先证明四边形是平行四边形,再证明有一对邻边互相垂直;二是直接证明四组邻边都互相垂直.规律总结:(1)很多时候我们都可以结合平行和垂直的充要条件确定多边形的形状,也可以由多边形的形状得到斜率之间的关系,最终求得多边形各顶点坐标.
(2)利用斜率判断三角形及四边形形状,首先要由各顶点坐标求出各边所在直线的斜率,再由斜率判断边与边的关系进而确定四边形形状. 已知直线l的方程为3x+4y-12=0,求直线l′的方程使
(1)l′与l平行,且过点(-1,3);
(2)l′与l垂直,且l′与两坐标轴围成的三角形面积为4.分析:利用一般式下两直线平行与垂直的条件,求解出未知直线的斜率,然后根据所给条件求出直线的方程.规律总结:(1)一般地,直线Ax+By+C=0中系数A,B确定直线的斜率,因此,与直线Ax+By+C=0平行的直线可设为Ax+By+m=0,这是常采用的解题技巧.我们称Ax+By+m=0是与直线Ax+By+C=0平行的直线系方程,参数m可以取m≠C的任意实数,这样就得到无数条与直线Ax+By+C=0平行的平行线系.当m=C时,Ax+By+m=0与Ax+By+C=0重合.
(2)一般地,经过点A(x0,y0),且与直线Ax+By+C=0平行的直线方程为A(x-x0)+B(y-y0)=0.(3)类似地有:与直线Ax+By+C=0垂直的直线系方程为Bx-Ay+m=0(A,B不同时为零).
(4)求解有关直线与坐标轴围成的三角形面积问题,我们可以设直线的截距式方程,直接利用截距写出三角形的面积,也可以利用设直线的其他形式的方程,求解出与坐标轴的交点坐标,然后写出三角形的面积.变式训练3.已知四边形ABCD的顶点为A(m,n),B(6,1),C(3,3),D(2,5),求m和n的值,使四边形ABCD为直角梯形.基础巩固两条直线平行1.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为__________.能力升级平行与垂直的简单应用9.在直角坐标平面内有两个点A(4,2),B(1,-2),在x轴上有点C,使∠ACB= ,则点C的坐标是__________.祝您学业有成
