2013-2014学年高中数学苏教版必修2同步辅导与检测:2.1.4两条直线的交点
文档属性
| 名称 | 2013-2014学年高中数学苏教版必修2同步辅导与检测:2.1.4两条直线的交点 |  | |
| 格式 | zip | ||
| 文件大小 | 599.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 20:40:21 | ||
图片预览








文档简介
课件23张PPT。2.1 直线与方程
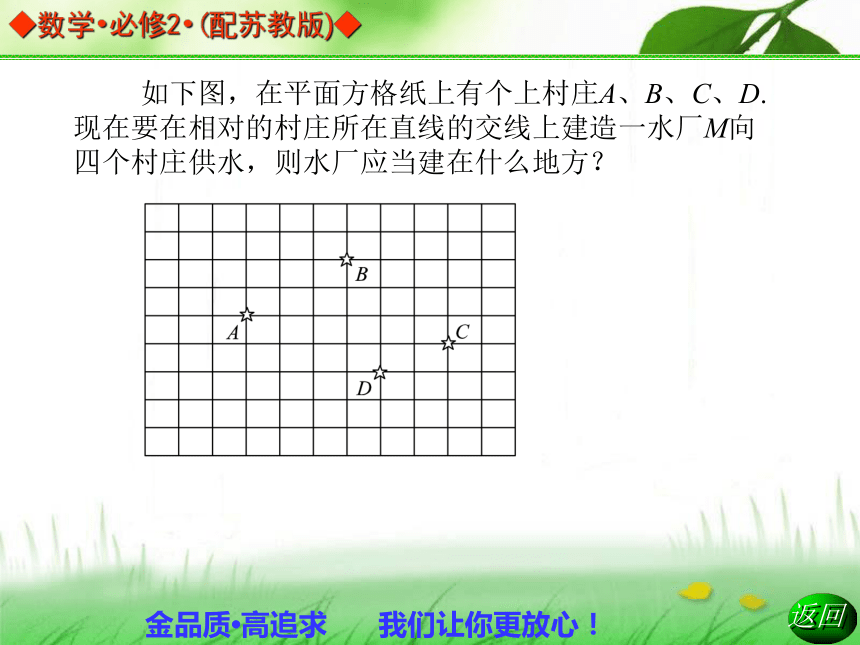
2.1.4 两条直线的交点 平面解析几何初步 如下图,在平面方格纸上有个上村庄A、B、C、D.现在要在相对的村庄所在直线的交线上建造一水厂M向四个村庄供水,则水厂应当建在什么地方?1.若直线l:Ax+By+C=0,点A(a,b),若点A在直线l上,则a、b的关系为__________.
2.在同一个平面内,两条直线有三种位置关系:____.相应的由直线方程组成的二元一次方程组的解也有三种情况:______.设两条直线的方程l1:Ax1+By1+C=0,l2:Ax2+By2+C=0,则这两条直线的方程所组成的方程组为
①若方程组①无解,则两直线l1,l2______,反之也成立;若方程组①有无穷多解,则直线l1,l2_____,反之也成立;若方程组①有唯一解,则两直线______,该解组成的有序实数对就是两条直线的________.
3.用代数法求两条直线的交点坐标的基本思路就是:首先写出由两条直线的方程所组成的方程组;然后_____求出方程组的解;最后写出两条直线的______.1.Aa+Bb+C=0
2.相交、平行、重合 有唯一解、无解、有无穷多解平行 重合 相交 交点坐标
3.解方程组 交点坐标该判断方法充分体现了直线交点的个数与相应二元一次方程组解的个数之间的一一对应关系,求两直线交点的一般步骤是:
①写出由两条直线的方程所组成的联立方程组;
②解方程组求出方程组的解;
③写出两条直线的交点坐标.
两条直线的交点即“形”的关系,可化归为方程组的解,即以“数”解“形”,这就是我们常说的数形结合思想.两条直线的交点问题 求经过两条直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0平行的直线方程.分析:可先求出交点坐标,再利用点斜式求方程,也可利用直线系方程表示出所求的方程,再结合两直线平行的充要条件求解.规律总结:两条直线的交点坐标就是直线方程组的解.本题解法一采用常规方法,先通过方程组求出两直线交点,再根据平行直线斜率相等,由点斜式求解;而解法二则采用了过直线A1x+B1y+C1=0与A2x+B2y+C2=0的交点的直线系方程:A1x+B1y+C1+λ(A2x+B2y+C2)=0.直接设出过两直线交点的方程,再根据平行条件求出待定系数即可.变式训练1.求过两条直线3x+4y-2=0与2x+y+2=0的交点且垂直于直线x-2y+3=0的直线方程.解析: 对称问题 △ABC的顶点A的坐标为(1,4),∠B、∠C平分线的方程分别为x-2y=0和x+y-1=0,求BC所在直线的方程.分析:该题求直线方程的条件不明显,如果能联想到初中平面几何有关角平分线的知识,就可以发现点A关于∠B、∠C平分线的对称点都在BC所在直线上,所以只要求出这两个对称点,利用两点式即可求出BC所在直线的方程.规律总结:点关于点对称问题是最基本的对称问题,用中点坐标公式求解,它是解答其他对称问题的基础.变式训练2.一条光线从点A(3,2)出发,经x轴反射,通过点B(-1,6),求入射光线和反射光线所在的直线方程.分析:设光线反射点为P,点A关于x轴的对称点为A′,根据光学上入射角等于反射角的原理可知点A′、P、B三点共线,因此,可用两点式求直线方程.基础巩固直线的交点1.直线3x+5y-1=0与直线4x+3y-5=0的交点是__________.解析:联立两直线方程解得交点坐标为(2,-1).
答案:(2,-1)能力升级求过直线交点的直线方程10.过直线2x-y+4=0与x-y+5=0的交点,且过(4,0)点的直线方程为__________.祝您学业有成
2.1.4 两条直线的交点 平面解析几何初步 如下图,在平面方格纸上有个上村庄A、B、C、D.现在要在相对的村庄所在直线的交线上建造一水厂M向四个村庄供水,则水厂应当建在什么地方?1.若直线l:Ax+By+C=0,点A(a,b),若点A在直线l上,则a、b的关系为__________.
2.在同一个平面内,两条直线有三种位置关系:____.相应的由直线方程组成的二元一次方程组的解也有三种情况:______.设两条直线的方程l1:Ax1+By1+C=0,l2:Ax2+By2+C=0,则这两条直线的方程所组成的方程组为
①若方程组①无解,则两直线l1,l2______,反之也成立;若方程组①有无穷多解,则直线l1,l2_____,反之也成立;若方程组①有唯一解,则两直线______,该解组成的有序实数对就是两条直线的________.
3.用代数法求两条直线的交点坐标的基本思路就是:首先写出由两条直线的方程所组成的方程组;然后_____求出方程组的解;最后写出两条直线的______.1.Aa+Bb+C=0
2.相交、平行、重合 有唯一解、无解、有无穷多解平行 重合 相交 交点坐标
3.解方程组 交点坐标该判断方法充分体现了直线交点的个数与相应二元一次方程组解的个数之间的一一对应关系,求两直线交点的一般步骤是:
①写出由两条直线的方程所组成的联立方程组;
②解方程组求出方程组的解;
③写出两条直线的交点坐标.
两条直线的交点即“形”的关系,可化归为方程组的解,即以“数”解“形”,这就是我们常说的数形结合思想.两条直线的交点问题 求经过两条直线2x-3y-3=0和x+y+2=0的交点且与直线3x+y-1=0平行的直线方程.分析:可先求出交点坐标,再利用点斜式求方程,也可利用直线系方程表示出所求的方程,再结合两直线平行的充要条件求解.规律总结:两条直线的交点坐标就是直线方程组的解.本题解法一采用常规方法,先通过方程组求出两直线交点,再根据平行直线斜率相等,由点斜式求解;而解法二则采用了过直线A1x+B1y+C1=0与A2x+B2y+C2=0的交点的直线系方程:A1x+B1y+C1+λ(A2x+B2y+C2)=0.直接设出过两直线交点的方程,再根据平行条件求出待定系数即可.变式训练1.求过两条直线3x+4y-2=0与2x+y+2=0的交点且垂直于直线x-2y+3=0的直线方程.解析: 对称问题 △ABC的顶点A的坐标为(1,4),∠B、∠C平分线的方程分别为x-2y=0和x+y-1=0,求BC所在直线的方程.分析:该题求直线方程的条件不明显,如果能联想到初中平面几何有关角平分线的知识,就可以发现点A关于∠B、∠C平分线的对称点都在BC所在直线上,所以只要求出这两个对称点,利用两点式即可求出BC所在直线的方程.规律总结:点关于点对称问题是最基本的对称问题,用中点坐标公式求解,它是解答其他对称问题的基础.变式训练2.一条光线从点A(3,2)出发,经x轴反射,通过点B(-1,6),求入射光线和反射光线所在的直线方程.分析:设光线反射点为P,点A关于x轴的对称点为A′,根据光学上入射角等于反射角的原理可知点A′、P、B三点共线,因此,可用两点式求直线方程.基础巩固直线的交点1.直线3x+5y-1=0与直线4x+3y-5=0的交点是__________.解析:联立两直线方程解得交点坐标为(2,-1).
答案:(2,-1)能力升级求过直线交点的直线方程10.过直线2x-y+4=0与x-y+5=0的交点,且过(4,0)点的直线方程为__________.祝您学业有成
