2013-2014学年高中数学苏教版必修2同步辅导与检测:2.2.2直线与圆的位置关系
文档属性
| 名称 | 2013-2014学年高中数学苏教版必修2同步辅导与检测:2.2.2直线与圆的位置关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 863.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 00:00:00 | ||
图片预览











文档简介
课件39张PPT。2.2 圆与方程
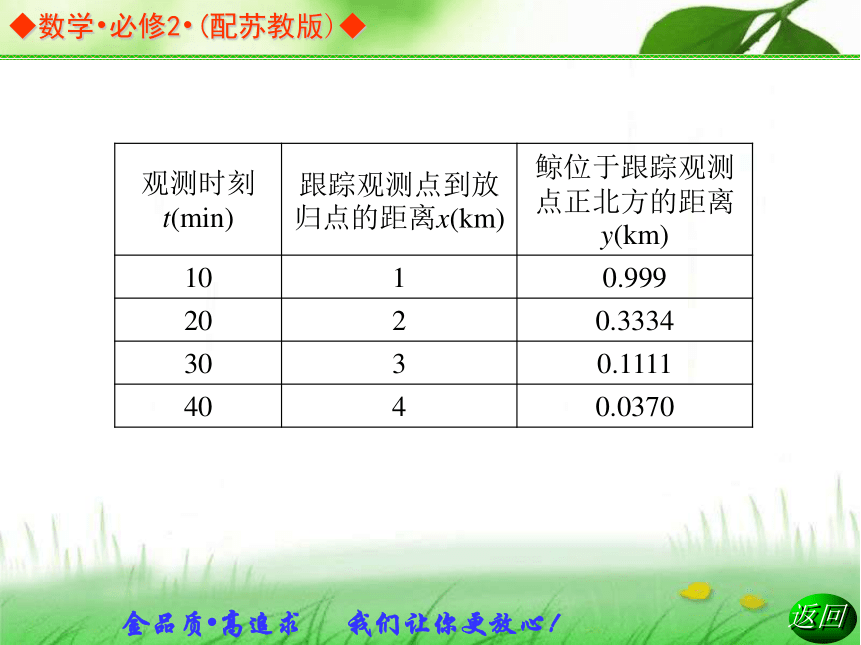
2.2.2 直线与圆的位置关系平面解析几何初步 为了更好地了解鲸的生活习性,某动物保护组织在受伤的鲸身上安装了电子监测装置,从海岸放归点A处(如下图所示)把它入归大海,并沿海岸线由西到东不停地对鲸进行了长达40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动).然后又在观测站B处对鲸进行生活习性的详细观测.已知AB=15 km,观测站B的观测半径为5 km.写出a,b近似满足的关系式,并预测:若按此关系式运动,那么鲸经过多长时间可进入观测站B的范围?1.直线与圆的位置关系有________、________、________三种.
2.(1)若直线与圆相交?圆心到直线的距离d________圆的半径r.
(2)若直线与圆相切?圆心到直线的距离d________圆的半径r.
(3)若直线与圆相离?圆心到直线的距离d________圆的半径r.1.相交 相切 相离
2.(1)< (2)= (3)>3.由方程组 消去y,可得关于x的一元二次方程2x2+2bx+b2-2=0,方程的根的判别式Δ=_____.
(1)当________时,Δ>0,方程组有两组不同的实数解,因此直线与圆相交;
(2)当________时,Δ=0,方程组有两组相同的实数解,因此直线与圆相切;
(3)当________时,Δ<0,方程组没有实数解,因此直线与圆相离.16-4b2 (1)-2(3)b<-2或b>24.若P(x0,y0)(y0≠0)是圆x2+y2=r2上一点,过P(x0,y0)的直线与圆相切,则切线的斜率为________,切线方程为____________.
5.过圆(x-a)2+(y-b)2=R2外一点P(x0,y0)作圆的切线PT(T为切点),则切线长PT=________.直线与圆的位置关系①直线与圆相交,有两个公共点;
②直线与圆相切,只有一个公共点;
③直线与圆相离,没有公共点.判定直线与圆的位置关系的方法圆中的弦长公式直线与圆位置关系的判定 已知圆x2+y2=8,定点P(4,0),问过P点的直线的斜率在什么范围内取值时,这条直线与已知圆:(1)相切;(2)相交;(3)相离.并写出过P点的切线方程.分析:(1)代数法:设出直线的点斜式方程,与圆的方程联立,根据直线与圆的位置关系确定Δ与0的关系,求出k的范围.
(2)几何法:设直线的点斜式方程,求出圆心到直线的距离d,根据直线与圆的位置关系确定d与r的大小,进而求出k的范围.解析:解法一:设过P点的直线的斜率为k(由已知k存在),则其方程为y=k(x-4).
由
消去y,得x2+k2(x-4)2=8,
即(1+k2)x2-8k2x+16k2-8=0,
Δ=(-8k2)2-4(1+k2)(16k2-8)=32(1-k2).
(1)令Δ=0,即32(1-k2)=0,解得k=±1.
∴当k=±1时,直线与圆相切,切线方程为x-y-4=0或x+y-4=0.(2)令Δ>0,即32(1-k2)>0,解得1-<k<1.
∴当-1<k<1时,直线与圆相交.
(3)令Δ<0,即32(1-k2)<0,解得k>1或k<-1.
当k>1或k<-1时,直线与圆相离.
解法二:设过P点直线的斜率为k(由已知k存在).则其方程为y=k(x-4),即kx-y-4k=0.变式训练1.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)证明直线l与圆相交;
(2)求直线l被圆C截得的弦长最小时,直线l的方程.切线方程 求经过点(1,-7)与圆x2+y2=25相切的切线方程.分析:显然点(1,-7)在圆外,因此可用点斜式方程求解,同时也可以求切点,利用两点式求切线方程.
解析:点(1,-7)代入圆方程12+(-7)2=50>25,过圆外一点与圆相切的切线方程求法有三种.解法一:设切线的斜率为k,由点斜式有y+7=k(x-1).
即y=k(x-1)-7,①
将①代入圆方程x2+y2=25得x2+[k(x-1)-7]2=25,
整理得(k2+1)x2-(2k2+14k)x+k2+14k+24=0,
Δ=(2k2+14k)2-4(k2+1)·(k2+14k+24)=0.
由此解出 再代回①可得切线方程为4x-3y-25=0或3x+4y+25=0,从过程可以看到:利用此法求切线方程,一般过程冗长,计算书写量大而繁杂,容易出现错误,通常情况下不用此法.解法三:设所求切线方程为x0x+y0y=25,将坐标 (1,-7)代入后得x0-7y0=25.
故所求切线方程为4x-3y-25=0或3x+4y+25=0.
规律总结:求切线一般有三种方法:(1)设切点,用切线公式法;(2)设切线斜率,用判别式法;(3)设切线斜率,用圆心到切线距离等于圆半径法.
一般地,过圆外一点可向圆作两条切线,在后两种方法中,应注意斜率不存在的情况.综合应用 根据气象台预报:在A市正东方向300 km的B处有一台风中心形成,并以40 km/h速度向西北方向移动,在距台风中心250 km以内的地区将受其影响,从现在起经过多长时间,台风将影响A市?持续时间多长(精确到0.1 h)?分析:解决实际问题的关键是如何把实际问题数学化,通常通过建系来实现.
解析:以A为圆心,
250 km为半径作⊙A.当台风中心移动所经过的直线l与⊙A相交或相切时,A市将受到台风影响.
建立如图所示的坐标系,那么点A、B的坐标分别为(0,0)、(300,0),⊙A的方程为x2+y2=2502,直线l的方程为y=-(x-300),即x+y-300=0(y≥0).规律总结:(1)在学习中要注意联系实际,重视数学在生产、生活及相关学科中的运用.
(2)解有关实际应用问题时,关键要明确题意,掌握建立数学模型的基本方法.
(3)数学实际应用问题,在多年来的高考中得到了重视,除了在选择、填空中出现外,近几年都有解答题出现,应引起重视,平时多做练习,以提高解决实际问题的能力.变式训练 2.设有半径为3 km的圆形村落,A,B两人同时从村落中心出发,A向东而B向北前进,A出村后不久,改变前进方向,斜着沿切于村落周界的方向前进,后来恰好与B相遇,设A、B两人的速度都一定,其比为3∶1,问A、B两人在何处相遇?解析:由题意可设A、B两人的速度分别为3v km/h、v km/h,再设A出发后x0小时,在点P处改变方向,又经y0小时,在点Q处与B相遇,则P、Q两点的坐标分别为(3vx0,0)、(0,vx0+vy0).由于A从P到Q行走的时间是y0小时,于是由勾股定理有OP2+OQ2=PQ2,有关最值问题规律总结:涉及与圆有关的最值问题,可借助图形性质,利用数形结合求解,对于:
①形如u= 的最值问题,可转化为动直线斜率的最值问题;
②形如l=ax+by的最值问题,可转化为动直线截距的最值问题;
③形如(x-a)2+(y-b)2的最值问题,可转化为圆上的点到已知定点(a,b)的距离的平方的最大值和最小值问题.变式训练3.圆x2+y2=1上的点到直线3x+4y-25=0的距离的最小值是________.4基础巩固直线与圆的位置关系1.已知直线x=a(a>0)和圆(x-1)2+y2=4相切,那么a的值是__________.解析:由已知|a-1|=2,∴a=3或a=-1,又a>0,∴a=3.
答案:3能力升级直线与圆的位置关系的判定7.直线3x-4y+6=0与圆(x-2)2+(y-3)2=4的位置关系是__________.祝您学业有成
2.2.2 直线与圆的位置关系平面解析几何初步 为了更好地了解鲸的生活习性,某动物保护组织在受伤的鲸身上安装了电子监测装置,从海岸放归点A处(如下图所示)把它入归大海,并沿海岸线由西到东不停地对鲸进行了长达40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动).然后又在观测站B处对鲸进行生活习性的详细观测.已知AB=15 km,观测站B的观测半径为5 km.写出a,b近似满足的关系式,并预测:若按此关系式运动,那么鲸经过多长时间可进入观测站B的范围?1.直线与圆的位置关系有________、________、________三种.
2.(1)若直线与圆相交?圆心到直线的距离d________圆的半径r.
(2)若直线与圆相切?圆心到直线的距离d________圆的半径r.
(3)若直线与圆相离?圆心到直线的距离d________圆的半径r.1.相交 相切 相离
2.(1)< (2)= (3)>3.由方程组 消去y,可得关于x的一元二次方程2x2+2bx+b2-2=0,方程的根的判别式Δ=_____.
(1)当________时,Δ>0,方程组有两组不同的实数解,因此直线与圆相交;
(2)当________时,Δ=0,方程组有两组相同的实数解,因此直线与圆相切;
(3)当________时,Δ<0,方程组没有实数解,因此直线与圆相离.16-4b2 (1)-2
5.过圆(x-a)2+(y-b)2=R2外一点P(x0,y0)作圆的切线PT(T为切点),则切线长PT=________.直线与圆的位置关系①直线与圆相交,有两个公共点;
②直线与圆相切,只有一个公共点;
③直线与圆相离,没有公共点.判定直线与圆的位置关系的方法圆中的弦长公式直线与圆位置关系的判定 已知圆x2+y2=8,定点P(4,0),问过P点的直线的斜率在什么范围内取值时,这条直线与已知圆:(1)相切;(2)相交;(3)相离.并写出过P点的切线方程.分析:(1)代数法:设出直线的点斜式方程,与圆的方程联立,根据直线与圆的位置关系确定Δ与0的关系,求出k的范围.
(2)几何法:设直线的点斜式方程,求出圆心到直线的距离d,根据直线与圆的位置关系确定d与r的大小,进而求出k的范围.解析:解法一:设过P点的直线的斜率为k(由已知k存在),则其方程为y=k(x-4).
由
消去y,得x2+k2(x-4)2=8,
即(1+k2)x2-8k2x+16k2-8=0,
Δ=(-8k2)2-4(1+k2)(16k2-8)=32(1-k2).
(1)令Δ=0,即32(1-k2)=0,解得k=±1.
∴当k=±1时,直线与圆相切,切线方程为x-y-4=0或x+y-4=0.(2)令Δ>0,即32(1-k2)>0,解得1-<k<1.
∴当-1<k<1时,直线与圆相交.
(3)令Δ<0,即32(1-k2)<0,解得k>1或k<-1.
当k>1或k<-1时,直线与圆相离.
解法二:设过P点直线的斜率为k(由已知k存在).则其方程为y=k(x-4),即kx-y-4k=0.变式训练1.已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).
(1)证明直线l与圆相交;
(2)求直线l被圆C截得的弦长最小时,直线l的方程.切线方程 求经过点(1,-7)与圆x2+y2=25相切的切线方程.分析:显然点(1,-7)在圆外,因此可用点斜式方程求解,同时也可以求切点,利用两点式求切线方程.
解析:点(1,-7)代入圆方程12+(-7)2=50>25,过圆外一点与圆相切的切线方程求法有三种.解法一:设切线的斜率为k,由点斜式有y+7=k(x-1).
即y=k(x-1)-7,①
将①代入圆方程x2+y2=25得x2+[k(x-1)-7]2=25,
整理得(k2+1)x2-(2k2+14k)x+k2+14k+24=0,
Δ=(2k2+14k)2-4(k2+1)·(k2+14k+24)=0.
由此解出 再代回①可得切线方程为4x-3y-25=0或3x+4y+25=0,从过程可以看到:利用此法求切线方程,一般过程冗长,计算书写量大而繁杂,容易出现错误,通常情况下不用此法.解法三:设所求切线方程为x0x+y0y=25,将坐标 (1,-7)代入后得x0-7y0=25.
故所求切线方程为4x-3y-25=0或3x+4y+25=0.
规律总结:求切线一般有三种方法:(1)设切点,用切线公式法;(2)设切线斜率,用判别式法;(3)设切线斜率,用圆心到切线距离等于圆半径法.
一般地,过圆外一点可向圆作两条切线,在后两种方法中,应注意斜率不存在的情况.综合应用 根据气象台预报:在A市正东方向300 km的B处有一台风中心形成,并以40 km/h速度向西北方向移动,在距台风中心250 km以内的地区将受其影响,从现在起经过多长时间,台风将影响A市?持续时间多长(精确到0.1 h)?分析:解决实际问题的关键是如何把实际问题数学化,通常通过建系来实现.
解析:以A为圆心,
250 km为半径作⊙A.当台风中心移动所经过的直线l与⊙A相交或相切时,A市将受到台风影响.
建立如图所示的坐标系,那么点A、B的坐标分别为(0,0)、(300,0),⊙A的方程为x2+y2=2502,直线l的方程为y=-(x-300),即x+y-300=0(y≥0).规律总结:(1)在学习中要注意联系实际,重视数学在生产、生活及相关学科中的运用.
(2)解有关实际应用问题时,关键要明确题意,掌握建立数学模型的基本方法.
(3)数学实际应用问题,在多年来的高考中得到了重视,除了在选择、填空中出现外,近几年都有解答题出现,应引起重视,平时多做练习,以提高解决实际问题的能力.变式训练 2.设有半径为3 km的圆形村落,A,B两人同时从村落中心出发,A向东而B向北前进,A出村后不久,改变前进方向,斜着沿切于村落周界的方向前进,后来恰好与B相遇,设A、B两人的速度都一定,其比为3∶1,问A、B两人在何处相遇?解析:由题意可设A、B两人的速度分别为3v km/h、v km/h,再设A出发后x0小时,在点P处改变方向,又经y0小时,在点Q处与B相遇,则P、Q两点的坐标分别为(3vx0,0)、(0,vx0+vy0).由于A从P到Q行走的时间是y0小时,于是由勾股定理有OP2+OQ2=PQ2,有关最值问题规律总结:涉及与圆有关的最值问题,可借助图形性质,利用数形结合求解,对于:
①形如u= 的最值问题,可转化为动直线斜率的最值问题;
②形如l=ax+by的最值问题,可转化为动直线截距的最值问题;
③形如(x-a)2+(y-b)2的最值问题,可转化为圆上的点到已知定点(a,b)的距离的平方的最大值和最小值问题.变式训练3.圆x2+y2=1上的点到直线3x+4y-25=0的距离的最小值是________.4基础巩固直线与圆的位置关系1.已知直线x=a(a>0)和圆(x-1)2+y2=4相切,那么a的值是__________.解析:由已知|a-1|=2,∴a=3或a=-1,又a>0,∴a=3.
答案:3能力升级直线与圆的位置关系的判定7.直线3x-4y+6=0与圆(x-2)2+(y-3)2=4的位置关系是__________.祝您学业有成
