2013-2014学年高中数学苏教版必修2同步辅导与检测:2.3.1空间直角坐标系
文档属性
| 名称 | 2013-2014学年高中数学苏教版必修2同步辅导与检测:2.3.1空间直角坐标系 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 20:38:24 | ||
图片预览







文档简介
课件25张PPT。2.3 空间直角坐标系
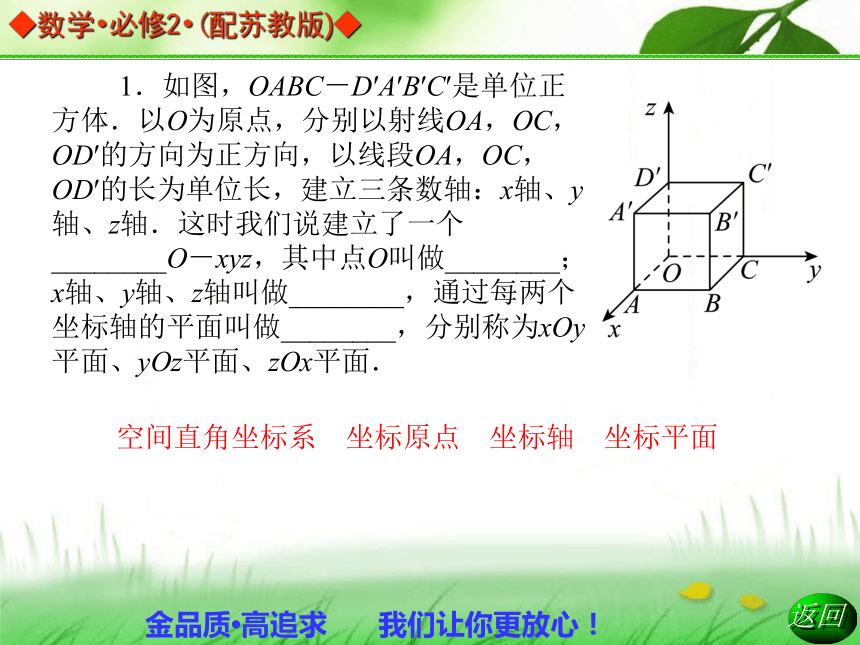
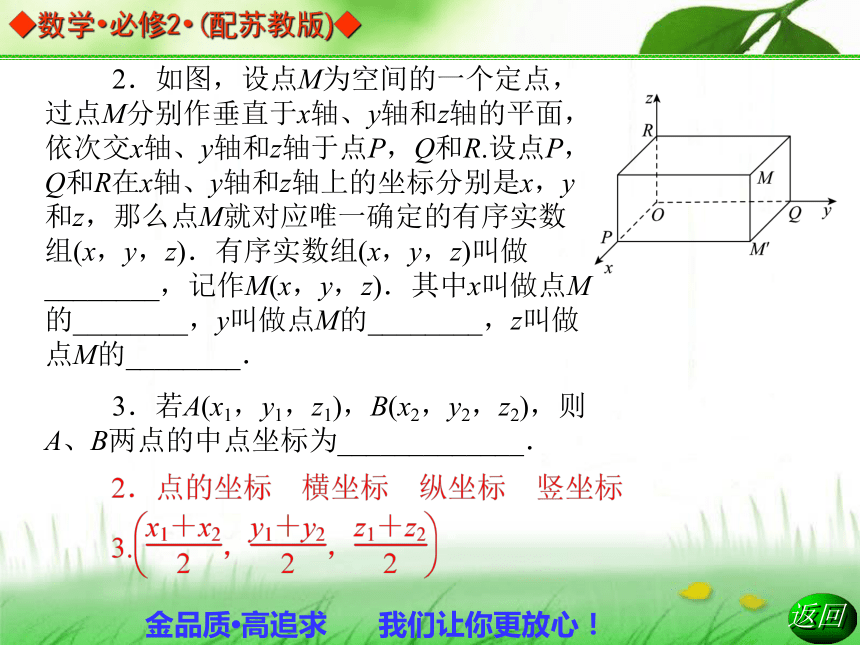
2.3.1 空间直角坐标系平面解析几何初步 或许你没有看过浩瀚无边的大海, 但是你一定看过美国作家海明威的著 名小说《老人与海》,其生动地描写 了一位老人,在汹涌澎湃的海面上, 孤身一人,与鲨鱼搏斗,最后战胜鲨 鱼的过程,尽管老人只能拖回一副鱼 骨头,但是他告诉我们“一个人可以被 毁灭,但不能被打败”.这是强者的精神宣言,然而,你是否思考过:当船航行在茫茫无际的大海上时,四周只见水,不见物,那么,怎样知道船所在的位置呢?怎样知道船离目的地还有多远呢?1.如图,OABC-D′A′B′C′是单位正方体.以O为原点,分别以射线OA,OC,OD′的方向为正方向,以线段OA,OC,OD′的长为单位长,建立三条数轴:x轴、y轴、z轴.这时我们说建立了一个________O-xyz,其中点O叫做________;x轴、y轴、z轴叫做________,通过每两个坐标轴的平面叫做________,分别称为xOy平面、yOz平面、zOx平面.空间直角坐标系 坐标原点 坐标轴 坐标平面2.如图,设点M为空间的一个定点,过点M分别作垂直于x轴、y轴和z轴的平面,依次交x轴、y轴和z轴于点P,Q和R.设点P,Q和R在x轴、y轴和z轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).有序实数组(x,y,z)叫做________,记作M(x,y,z).其中x叫做点M的________,y叫做点M的________,z叫做点M的________.
3.若A(x1,y1,z1),B(x2,y2,z2),则A、B两点的中点坐标为_____________.空间直角坐标系①空间直角坐标系:从空间某一个定点O引三条互相垂直且有相同单位长度的数轴Ox、Oy、Oz,这样的坐标系叫做空间直角坐标系O-xyz.点O叫做坐标原点,x轴、y轴和z轴叫做坐标轴.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy平面、yOz平面和zOx平面.
②右手直角坐标系:在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
③空间直角坐标系中的坐标:对于空间任一点M,作出M点在三条坐标轴Ox轴、Oy轴、Oz轴上的射影,其相应数轴上的坐标依次为x、y、z,则把有序实数对(x,y,z)叫做M点在此空间直角坐标系中的坐标记作M(x,y,z),其中x叫做点M的横坐标,y叫做点M的纵坐标,z叫做点M的竖坐标.④xOy平面(通过x轴和y轴的平面)是坐标形如(x,y,0)的点构成的点集,其中x,y为任意的实数;xOz平面(通过x轴和z轴的平面)是坐标形如(x,0,z)的点构成的点集,其中x,z为任意的实数;yOz平面(通过y轴和z轴的平面)是坐标形如(0,y,z)的点构成的点集,其中y,z为任意的实数.
⑤x轴是坐标形如(x,0,0)的点构成的点集,其中x为任意实数;
y轴是坐标形如(0,y,0)的点构成的点集,其中y为任意实数;
z轴是坐标形如(0,0,z)的点构成的点集,其中z为任意实数.
空间直角坐标系中与平面直角坐标中重要结论对照表(设P为(x,y,z)或(x,y))空间直角坐标系 如右图在正方体ABCD-A1B1C1D1中,E、F分别是BB1,D1B1的中点,棱长为1.求E,F点的坐标.分析:以正方体顶点为坐标原点,建立坐标系.给出顶点D1、B1、B的坐标,利用中点坐标公式写出E、F点的坐标.
解析:建立如下图所示的坐标系.规律总结:(1)能准确地确定空间任意一点的直角坐标是利用空间直角坐标的基础,因此一定要掌握如下方法:过点M分别作三个坐标平面的平行平面(或垂面),分别交坐标轴于A、B、C三点,确定x、y、z.具体理解可以以长方体为模型来进行,要注意掌握一些特殊点(如落在坐标轴上的点和落在坐标平面上的点)的坐标表示的特征.
(2)熟记坐标轴上的点的坐标和坐标平面上的坐标表示的特征.变式训练1.如下图,在棱长为a的正方体OABC-D'A'B'C'中,对角线OB′与BD′相交于点Q.顶点O为坐标原点,OA,OC分别在x轴、y轴正半轴上,试写出点Q的坐标.解析:空间中点对称问题 求点A(1,2,-1)关于坐标平面xOy及x轴对称的点的坐标.分析:解决本题的关键是明确各坐标轴,各坐标平面对称的两点,其点的坐标的分量的关系,可借助于图形.解析:如右图所示,过A作AM⊥xOy交平面于M,并延长到C,使AM=CM,则A与C关于坐标平面xOy对称,且C(1,2,1).
过A作AN⊥x轴于N并延长到点B,使AN=NB,则A与B关于x轴对称且B(1,-2,1).
∴A(1,2,-1)关于坐标平面xOy对称的点C(1,2,1);
A(1,2,-1)关于x轴对称的点B(1,-2,1).
规律总结:对称关系可简记为“关于谁对称谁不变,其余的均相反”.特别地,关于原点对称,三个坐标符号都要变.变式训练2.在空间直角坐标系中,给定点M(1,-2,3),求它分别关于坐标平面、坐标轴和原点的对称点的坐标.解析:(1)关于xOy平面的对称点坐标为(1,-2,-3);
关于xOz平面的对称点坐标为(1,2,3);
关于yOz平面的对称点坐标为(-1,-2,3);
(2)关于x轴的对称点坐标为(1,2,-3);
关于y轴的对称点坐标为(-1,-2,-3);
关于z轴的对称点坐标为(-1,2,3);
(3)关于原点的对称点坐标为(-1,2,-3).空间直角坐标系的应用 晶体的基本单位称为晶胞,如下图(1)是食盐晶胞的示意图(可看成八个棱长为的小正方体堆积成的正方体),其中黑点代表纳原子,如下图(2),建立空间直角坐标系O-xyz后,试写出全部钠原子所在位置的坐标.基础巩固空间中点的位置的确定1.点A(0,-2,3)在空间直角坐标系的位置是在________上.解析:∵xA=0,∴A在yOz平面上.
答案:yOz平面能力升级求空间中点的坐标10.如右图三棱锥OABC为一个正方体截下的一角,OA=a,OB=b,OC=c,建立如图所示的坐标系,则△ABC的重心G的坐标是________.祝您学业有成
2.3.1 空间直角坐标系平面解析几何初步 或许你没有看过浩瀚无边的大海, 但是你一定看过美国作家海明威的著 名小说《老人与海》,其生动地描写 了一位老人,在汹涌澎湃的海面上, 孤身一人,与鲨鱼搏斗,最后战胜鲨 鱼的过程,尽管老人只能拖回一副鱼 骨头,但是他告诉我们“一个人可以被 毁灭,但不能被打败”.这是强者的精神宣言,然而,你是否思考过:当船航行在茫茫无际的大海上时,四周只见水,不见物,那么,怎样知道船所在的位置呢?怎样知道船离目的地还有多远呢?1.如图,OABC-D′A′B′C′是单位正方体.以O为原点,分别以射线OA,OC,OD′的方向为正方向,以线段OA,OC,OD′的长为单位长,建立三条数轴:x轴、y轴、z轴.这时我们说建立了一个________O-xyz,其中点O叫做________;x轴、y轴、z轴叫做________,通过每两个坐标轴的平面叫做________,分别称为xOy平面、yOz平面、zOx平面.空间直角坐标系 坐标原点 坐标轴 坐标平面2.如图,设点M为空间的一个定点,过点M分别作垂直于x轴、y轴和z轴的平面,依次交x轴、y轴和z轴于点P,Q和R.设点P,Q和R在x轴、y轴和z轴上的坐标分别是x,y和z,那么点M就对应唯一确定的有序实数组(x,y,z).有序实数组(x,y,z)叫做________,记作M(x,y,z).其中x叫做点M的________,y叫做点M的________,z叫做点M的________.
3.若A(x1,y1,z1),B(x2,y2,z2),则A、B两点的中点坐标为_____________.空间直角坐标系①空间直角坐标系:从空间某一个定点O引三条互相垂直且有相同单位长度的数轴Ox、Oy、Oz,这样的坐标系叫做空间直角坐标系O-xyz.点O叫做坐标原点,x轴、y轴和z轴叫做坐标轴.通过每两个坐标轴的平面叫做坐标平面,分别称为xOy平面、yOz平面和zOx平面.
②右手直角坐标系:在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
③空间直角坐标系中的坐标:对于空间任一点M,作出M点在三条坐标轴Ox轴、Oy轴、Oz轴上的射影,其相应数轴上的坐标依次为x、y、z,则把有序实数对(x,y,z)叫做M点在此空间直角坐标系中的坐标记作M(x,y,z),其中x叫做点M的横坐标,y叫做点M的纵坐标,z叫做点M的竖坐标.④xOy平面(通过x轴和y轴的平面)是坐标形如(x,y,0)的点构成的点集,其中x,y为任意的实数;xOz平面(通过x轴和z轴的平面)是坐标形如(x,0,z)的点构成的点集,其中x,z为任意的实数;yOz平面(通过y轴和z轴的平面)是坐标形如(0,y,z)的点构成的点集,其中y,z为任意的实数.
⑤x轴是坐标形如(x,0,0)的点构成的点集,其中x为任意实数;
y轴是坐标形如(0,y,0)的点构成的点集,其中y为任意实数;
z轴是坐标形如(0,0,z)的点构成的点集,其中z为任意实数.
空间直角坐标系中与平面直角坐标中重要结论对照表(设P为(x,y,z)或(x,y))空间直角坐标系 如右图在正方体ABCD-A1B1C1D1中,E、F分别是BB1,D1B1的中点,棱长为1.求E,F点的坐标.分析:以正方体顶点为坐标原点,建立坐标系.给出顶点D1、B1、B的坐标,利用中点坐标公式写出E、F点的坐标.
解析:建立如下图所示的坐标系.规律总结:(1)能准确地确定空间任意一点的直角坐标是利用空间直角坐标的基础,因此一定要掌握如下方法:过点M分别作三个坐标平面的平行平面(或垂面),分别交坐标轴于A、B、C三点,确定x、y、z.具体理解可以以长方体为模型来进行,要注意掌握一些特殊点(如落在坐标轴上的点和落在坐标平面上的点)的坐标表示的特征.
(2)熟记坐标轴上的点的坐标和坐标平面上的坐标表示的特征.变式训练1.如下图,在棱长为a的正方体OABC-D'A'B'C'中,对角线OB′与BD′相交于点Q.顶点O为坐标原点,OA,OC分别在x轴、y轴正半轴上,试写出点Q的坐标.解析:空间中点对称问题 求点A(1,2,-1)关于坐标平面xOy及x轴对称的点的坐标.分析:解决本题的关键是明确各坐标轴,各坐标平面对称的两点,其点的坐标的分量的关系,可借助于图形.解析:如右图所示,过A作AM⊥xOy交平面于M,并延长到C,使AM=CM,则A与C关于坐标平面xOy对称,且C(1,2,1).
过A作AN⊥x轴于N并延长到点B,使AN=NB,则A与B关于x轴对称且B(1,-2,1).
∴A(1,2,-1)关于坐标平面xOy对称的点C(1,2,1);
A(1,2,-1)关于x轴对称的点B(1,-2,1).
规律总结:对称关系可简记为“关于谁对称谁不变,其余的均相反”.特别地,关于原点对称,三个坐标符号都要变.变式训练2.在空间直角坐标系中,给定点M(1,-2,3),求它分别关于坐标平面、坐标轴和原点的对称点的坐标.解析:(1)关于xOy平面的对称点坐标为(1,-2,-3);
关于xOz平面的对称点坐标为(1,2,3);
关于yOz平面的对称点坐标为(-1,-2,3);
(2)关于x轴的对称点坐标为(1,2,-3);
关于y轴的对称点坐标为(-1,-2,-3);
关于z轴的对称点坐标为(-1,2,3);
(3)关于原点的对称点坐标为(-1,2,-3).空间直角坐标系的应用 晶体的基本单位称为晶胞,如下图(1)是食盐晶胞的示意图(可看成八个棱长为的小正方体堆积成的正方体),其中黑点代表纳原子,如下图(2),建立空间直角坐标系O-xyz后,试写出全部钠原子所在位置的坐标.基础巩固空间中点的位置的确定1.点A(0,-2,3)在空间直角坐标系的位置是在________上.解析:∵xA=0,∴A在yOz平面上.
答案:yOz平面能力升级求空间中点的坐标10.如右图三棱锥OABC为一个正方体截下的一角,OA=a,OB=b,OC=c,建立如图所示的坐标系,则△ABC的重心G的坐标是________.祝您学业有成
