2013-2014学年高中数学苏教版必修5同步辅导与检测:1.2余弦定理
文档属性
| 名称 | 2013-2014学年高中数学苏教版必修5同步辅导与检测:1.2余弦定理 |  | |
| 格式 | zip | ||
| 文件大小 | 588.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 20:31:20 | ||
图片预览











文档简介
课件35张PPT。1.2 余弦定理解三角形 前节学习正弦定理,可以解决三角形中的两类问题:已知两角及一边,求其余边角;已知两边和其中一边的对角,求其余边角.那么在三角形中的其他情况和由三边能否求其余边角?由两边和夹角呢?△ABC中,已知边a,b及∠C.
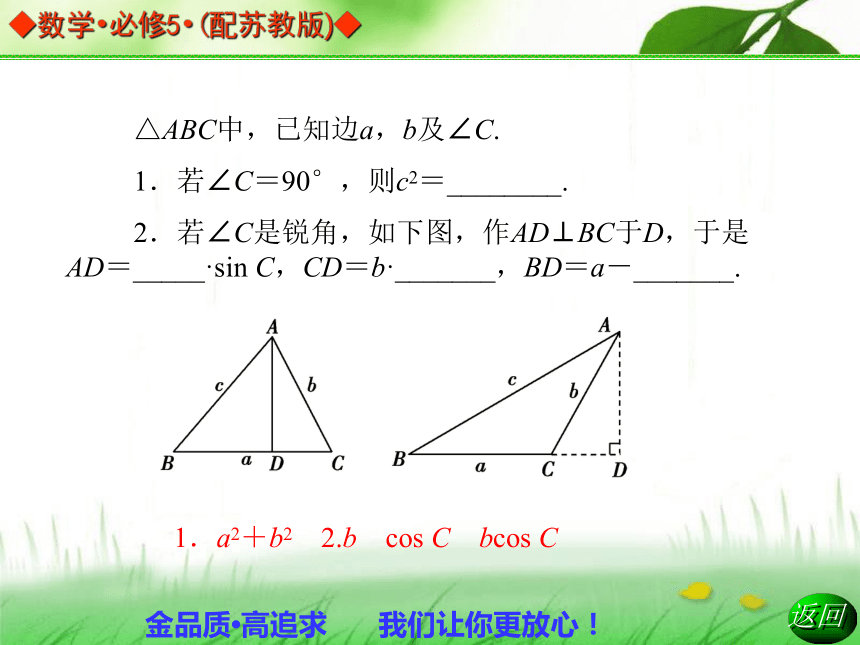
1.若∠C=90°,则c2=________.
2.若∠C是锐角,如下图,作AD⊥BC于D,于是AD=_____·sin C,CD=b·_______,BD=a-_______.1.a2+b2 2.b cos C bcos C3.若∠C为钝角,如上图作AD⊥BC,与BC的延长线相交于D,此时AD=________·sin(π-C)=b·________,CD=b·cos________=-bcos C.
4.在△ABC中,已知边a、b及∠C,由c2=a2+b2-2abcos C可得cos C=________.
5.结论“三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍”,称为________.6.根据cos C= 可知,当a2+b27.若△ABC是锐角三角形,则a2+b2____c2.>钝角余弦定理证明材料中利用几何法通过构造直角三角形,利用勾股定理证明了余弦定理.对定理的证明还可通过向量法、解析法等.证法二:(解析法)如右图(2)以A点为原点,以△ABC的边AB所在直线为x轴,以过A与AB垂直的直线为y轴,建立直角坐标系,则A(0,0),C(bcos A,bsin A),B(c,0),由两点间的距离公式得BC2=(bcos A-c)2+(bsin A-0)2,
a2=b2cos2A-2bccos A+c2+b2sin2A,
即a2=b2+c2-2bccos A.
同理可证:b2=a2+c2-2accos B,c2=a2+b2-2abcos C.证法三:(用正弦定理证明)
因为b=2Rsin B,c=2Rsin C,
所以b2+c2-2bccos A=4R2(sin2B+sin2C-2sin Bsin Ccos A)
=4R2[sin2B+sin2C+2sin Bsin Ccos(B+C)]
=4R2[sin2B+sin2C-2sin2Bsin2C+2sin Bsin Ccos Bcos C]
=4R2[sin2B(1-sin2C)+sin2C(1-sin2B)+2sin Bsin Ccos Bcos C]
=4R2(sin2 Bcos2C+2sin Bsin Ccos Bcos C+sin2 Ccos2B)
=4R2sin2 (B+C)=4R2sin2A=a2.
同理可证b2=a2+c2-2accos B,c2=a2+b2-2abcos C.余弦定理及其应用在解三角形问题时,需掌握的三角关系式在△ABC中,以下的三角关系式,在解答有关的三角形问题时,经常用到,要记准、记熟、灵活地加以运用.
A+B+C=π;
sin(A+B)=sin C,cos(A+B)=-cos C;已知边角解三角形分析:已知三边,可用余弦定理直接求角,先求出两个角后,再用内角和求第三个角.
使用余弦定理求角时,一般在判断三条边的大小后,可先求最大角,也可先求最小角,如果最大角小于60°,最小角大于60°,可知三角形无解.变式迁移 已知三角形ABC中,b=3,c=3 ,B=30°,则a=______.名师点评:本题是在已知两边及其中一边对角的条件下解三角形.一般情况下,利用正弦定理先求出∠C,再求∠A,最后求a,需要讨论.如果采用余弦定理来解,只需解一个一元二次方程,即可求得a,比较解法一、解法二,解法二比较简单.变式迁移2.在△ABC中,a=1,b=1,C=120°,求c.利用余弦定理判断三角形形状 在△ABC中,若tan A∶tan B=a2∶b2,试判断△ABC的形状.分析:可从问题已知条件出发,寻找三角形的边与边或角与角之间的关系,然后判断之.名师点评:已知三角形中的边角关系式,判断三角形的形状,有两种思路:其一化边为角,再进行三角恒等变换,求出三个角之间的关系式;其二化角为边,再进行代数恒等变换,求出三条边之间的关系式.两种转化主要应用正弦定理和余弦定理.
本题的两种解法,就是通过两种不同的转化来实现的.变式迁移3.若△ABC的三个内角满足sin A ∶ sin B ∶sin C=5∶11∶13,则△ABC( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.可能是锐角三角形,也可能是钝角三角形方程思想的应用 如图所示,在△ABC中,已知BC=15,AB∶AC=7∶8,sin B= ,求BC边上的高. 分析:由已知设AB=7x,
AC=8x,故要求AD的长只要求出x,△ABC中已知三边只需再有一个角,根据余弦定理便可求x,而用正弦定理正好可求角C.名师点评:比例式的设法是一种解题技巧,如a∶b∶c=3∶4∶5,可设a=3x,b=4x,c=5x,这种设法可使运算方便,必须学会.变式迁移4.在△ABC中,若c=4,b=7,BC边上的中线AD之长为 ,求边长a.基础巩固祝您学业有成
1.若∠C=90°,则c2=________.
2.若∠C是锐角,如下图,作AD⊥BC于D,于是AD=_____·sin C,CD=b·_______,BD=a-_______.1.a2+b2 2.b cos C bcos C3.若∠C为钝角,如上图作AD⊥BC,与BC的延长线相交于D,此时AD=________·sin(π-C)=b·________,CD=b·cos________=-bcos C.
4.在△ABC中,已知边a、b及∠C,由c2=a2+b2-2abcos C可得cos C=________.
5.结论“三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍”,称为________.6.根据cos C= 可知,当a2+b2
a2=b2cos2A-2bccos A+c2+b2sin2A,
即a2=b2+c2-2bccos A.
同理可证:b2=a2+c2-2accos B,c2=a2+b2-2abcos C.证法三:(用正弦定理证明)
因为b=2Rsin B,c=2Rsin C,
所以b2+c2-2bccos A=4R2(sin2B+sin2C-2sin Bsin Ccos A)
=4R2[sin2B+sin2C+2sin Bsin Ccos(B+C)]
=4R2[sin2B+sin2C-2sin2Bsin2C+2sin Bsin Ccos Bcos C]
=4R2[sin2B(1-sin2C)+sin2C(1-sin2B)+2sin Bsin Ccos Bcos C]
=4R2(sin2 Bcos2C+2sin Bsin Ccos Bcos C+sin2 Ccos2B)
=4R2sin2 (B+C)=4R2sin2A=a2.
同理可证b2=a2+c2-2accos B,c2=a2+b2-2abcos C.余弦定理及其应用在解三角形问题时,需掌握的三角关系式在△ABC中,以下的三角关系式,在解答有关的三角形问题时,经常用到,要记准、记熟、灵活地加以运用.
A+B+C=π;
sin(A+B)=sin C,cos(A+B)=-cos C;已知边角解三角形分析:已知三边,可用余弦定理直接求角,先求出两个角后,再用内角和求第三个角.
使用余弦定理求角时,一般在判断三条边的大小后,可先求最大角,也可先求最小角,如果最大角小于60°,最小角大于60°,可知三角形无解.变式迁移 已知三角形ABC中,b=3,c=3 ,B=30°,则a=______.名师点评:本题是在已知两边及其中一边对角的条件下解三角形.一般情况下,利用正弦定理先求出∠C,再求∠A,最后求a,需要讨论.如果采用余弦定理来解,只需解一个一元二次方程,即可求得a,比较解法一、解法二,解法二比较简单.变式迁移2.在△ABC中,a=1,b=1,C=120°,求c.利用余弦定理判断三角形形状 在△ABC中,若tan A∶tan B=a2∶b2,试判断△ABC的形状.分析:可从问题已知条件出发,寻找三角形的边与边或角与角之间的关系,然后判断之.名师点评:已知三角形中的边角关系式,判断三角形的形状,有两种思路:其一化边为角,再进行三角恒等变换,求出三个角之间的关系式;其二化角为边,再进行代数恒等变换,求出三条边之间的关系式.两种转化主要应用正弦定理和余弦定理.
本题的两种解法,就是通过两种不同的转化来实现的.变式迁移3.若△ABC的三个内角满足sin A ∶ sin B ∶sin C=5∶11∶13,则△ABC( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.可能是锐角三角形,也可能是钝角三角形方程思想的应用 如图所示,在△ABC中,已知BC=15,AB∶AC=7∶8,sin B= ,求BC边上的高. 分析:由已知设AB=7x,
AC=8x,故要求AD的长只要求出x,△ABC中已知三边只需再有一个角,根据余弦定理便可求x,而用正弦定理正好可求角C.名师点评:比例式的设法是一种解题技巧,如a∶b∶c=3∶4∶5,可设a=3x,b=4x,c=5x,这种设法可使运算方便,必须学会.变式迁移4.在△ABC中,若c=4,b=7,BC边上的中线AD之长为 ,求边长a.基础巩固祝您学业有成
