2013-2014学年高中数学苏教版必修5同步辅导与检测:1.3正弦定理、余弦定理的应用
文档属性
| 名称 | 2013-2014学年高中数学苏教版必修5同步辅导与检测:1.3正弦定理、余弦定理的应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 681.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 00:00:00 | ||
图片预览











文档简介
课件34张PPT。1.3 正弦定理、余弦定理的应用 解三角形 2006年10月12日,中国宣布了自己的探月计划:中国将在2007年把“嫦娥一号”绕月卫星送入太空,2012年实现发射软着陆器登陆月球.路透社报道:中国将在2024年把人送上月球.
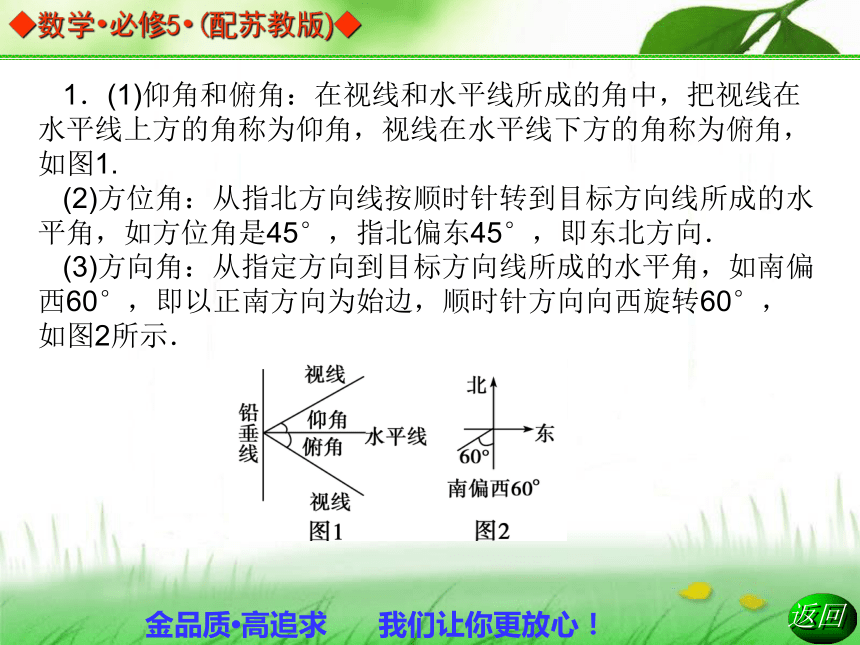
登陆月球如此困难,除了存在很多科学难题外还因为月球与地球相距很远,有38万公里.很久以前,数学家们就测量计算出了这个距离.你知道他们是如何计算的吗?这就要利用解斜三角形的知识.1.(1)仰角和俯角:在视线和水平线所成的角中,把视线在水平线上方的角称为仰角,视线在水平线下方的角称为俯角,如图1.
(2)方位角:从指北方向线按顺时针转到目标方向线所成的水平角,如方位角是45°,指北偏东45°,即东北方向.
(3)方向角:从指定方向到目标方向线所成的水平角,如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°,如图2所示.(4)李强出校门向东,前进200米,再向北走200米便回到家中,李强家在学校的哪个方向?
答案:东偏北45度方向200米处.
2.地面上三个点A、B、C,若B在A正北方向上,C在A北偏东20°方向上,C在B东偏北25°方向上,则C在A东偏北70°方向上,C在B北偏东65°方向上,A在C西偏南70°方向上,B在C西偏南25°方向上,B在C南偏西65°方向上.
3.(1)山下B点望山上A点仰角为30°,则山上A点望山下B点俯角为30°.
(2)方位角是指从正北方向顺时针旋转到达目标方向的水平角.若水平面上点A处测得点B的方位角是120°,则点B在点A东偏南30°方向上.
4.(1)A点望B、C的视角是指∠BAC的大小.
(2)在△ABC中,A=105°,B=30°,则C点望A、B的视角为45°.
5.(1)坡度是指斜坡所在平面与水平面的夹角.
(2)沿坡度为30°的斜坡直线向上行走100米,实际升高了50米.
6.东北方向是指东偏北45°的方向.10.设Rt△ABC的两直角边长为a,b,则它的内切圆半径r=(a+b-).
11.设△ABC的周长为2p,内切圆半径为r,则△ABC的面积=pr.
12.S=absin C=acsin B=bcsin A.
解斜三角形应用题的步骤(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如坡度、仰角、俯角、视角、象限角、方位角、方向角等.
(2)根据题意画出图形.
(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要算法简练、计算准确,最后作答.在实际应用中的有关名称、术语 实际应用问题中有关的名称、术语
(1)仰角和俯角:与目标视线在同一铅直平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角.
(2)方向角:从指定方向线到目标方向线的水平角.
(3)方位角:从指北方向线顺时针到目标方向线的水平角.
(4)坡度:坡面与水平面所成的二面角的度数.三角形中有关公式还需要熟悉两角和与差的正弦、余弦、正切及二倍角的正弦、余弦、正切公式.需注意问题(1)会在各种应用题中,抽象或构造出三角形,标出已知量、未知量,确定解三角形的方法,灵活选用正、余弦定理解之.
(2)搞清利用解斜三角形可解决的各类应用问题的基本图形和相等关系.
(3)理解各种应用问题中的有关名词、术语,如坡角、俯角、仰角、方向角、方位角等.
(4)会利用经纬仪器及皮尺等测量工具进行实地测量,会按照要求写实习报告,会用计算器计算测量结果,提高动手操作能力及数学语言表达能力.求不可到达两点间距离 隔河有两目标A与B但不能到达,在岸边选取相距 km的C、D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内).求两目标A,B之间的距离.分析:由题意作出平面示意图(如右图所示),在四边形ABCD中,需由已知条件求出AB的长.由图形可知,在△ACD与△BCD中,利用正弦定理可求得AC与BC,然后在△ABC中,由余弦定理可求出AB.名师点评:如果涉及解多个三角形的问题,在解题中就应注意解题过程的优化.如求AB的长,也可选择在△ABD中应用余弦定理求解,但此时必须求出AD与BD的长,显然求AD不如求AC容易,另外,本题没有要求取近似值,故不应将写成2.236.变式迁移在某海滨城市附近海面上有一台风,据监测,当前台风中心位于城市O东偏南α角方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动,台风侵袭的半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?正、余弦定理在追击问题中的应用分析:在解题前必须画出示意图,但应该明确以下几个概念:其一是方位角;其二是沿什么方向追,即按什么方位角航行;其三是最快追上,即应理解为按直线航行,且两船所用时间相等.在此基础上,通过解三角形,即可求出CD的方位角及由C到D所需的航行时间. 在海岸A处,发现北偏东45°方向,距A为( -1) km的B处有一艘走私船.在A处北偏西75°方向,距A为2 km的C处的缉私船奉命以10 km/h的速度追截走私船.此时走私船正以10 km/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.名师点评:解题时应明确,方位角是相对每一点而言的,因此,从这个意义上来说,方位角是一个动态角,在理解题意时,应把方位角看活,否则在理解题意上将可能产生失误.变式训练 2.如右图所示,一缉私艇
在A处发现在北偏东45°方向,
距离12 n mile的海面上有一走
私船C正以10 n mile/h的速度
沿东偏南15°方向逃窜.
缉私艇的速度为14 n mile/h,若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追及所需的时间和α角的正弦值.正、余弦定理的综合运用 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100 m后,又从B点测得斜度为45°,设建筑物的高为50 m,求此山对于地平面的斜度的倾斜角θ.(提示:cos 42.94°= -1)分析:设山对于地平面的斜度的倾斜角∠EAD=θ,这样可在△ABC中利用正弦定理求出BC;再在△BCD中,利用正弦定理得到关于θ的三角函数等式,进而解出θ角.名师点评:解应用题,首先要增强应用数学的意识.解应用题可分两步:第一步,先分析问题,抓住实际问题中的数量关系,将其转化成一般数学问题;第二步,利用所学知识和方法解决这个数学问题,其中的关键在于如何将实际问题数学化,也就是说如何将实际问题等价转化成一个数学问题.变式训练 3.如图所示,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12 n mile,在A处看灯塔C在货轮北偏西30°,距离为8 n mile,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:(1)A处与D处的距离;(2)灯塔C与D处的距离.祝您学业有成
登陆月球如此困难,除了存在很多科学难题外还因为月球与地球相距很远,有38万公里.很久以前,数学家们就测量计算出了这个距离.你知道他们是如何计算的吗?这就要利用解斜三角形的知识.1.(1)仰角和俯角:在视线和水平线所成的角中,把视线在水平线上方的角称为仰角,视线在水平线下方的角称为俯角,如图1.
(2)方位角:从指北方向线按顺时针转到目标方向线所成的水平角,如方位角是45°,指北偏东45°,即东北方向.
(3)方向角:从指定方向到目标方向线所成的水平角,如南偏西60°,即以正南方向为始边,顺时针方向向西旋转60°,如图2所示.(4)李强出校门向东,前进200米,再向北走200米便回到家中,李强家在学校的哪个方向?
答案:东偏北45度方向200米处.
2.地面上三个点A、B、C,若B在A正北方向上,C在A北偏东20°方向上,C在B东偏北25°方向上,则C在A东偏北70°方向上,C在B北偏东65°方向上,A在C西偏南70°方向上,B在C西偏南25°方向上,B在C南偏西65°方向上.
3.(1)山下B点望山上A点仰角为30°,则山上A点望山下B点俯角为30°.
(2)方位角是指从正北方向顺时针旋转到达目标方向的水平角.若水平面上点A处测得点B的方位角是120°,则点B在点A东偏南30°方向上.
4.(1)A点望B、C的视角是指∠BAC的大小.
(2)在△ABC中,A=105°,B=30°,则C点望A、B的视角为45°.
5.(1)坡度是指斜坡所在平面与水平面的夹角.
(2)沿坡度为30°的斜坡直线向上行走100米,实际升高了50米.
6.东北方向是指东偏北45°的方向.10.设Rt△ABC的两直角边长为a,b,则它的内切圆半径r=(a+b-).
11.设△ABC的周长为2p,内切圆半径为r,则△ABC的面积=pr.
12.S=absin C=acsin B=bcsin A.
解斜三角形应用题的步骤(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如坡度、仰角、俯角、视角、象限角、方位角、方向角等.
(2)根据题意画出图形.
(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要算法简练、计算准确,最后作答.在实际应用中的有关名称、术语 实际应用问题中有关的名称、术语
(1)仰角和俯角:与目标视线在同一铅直平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫仰角,目标视线在水平视线下方时叫俯角.
(2)方向角:从指定方向线到目标方向线的水平角.
(3)方位角:从指北方向线顺时针到目标方向线的水平角.
(4)坡度:坡面与水平面所成的二面角的度数.三角形中有关公式还需要熟悉两角和与差的正弦、余弦、正切及二倍角的正弦、余弦、正切公式.需注意问题(1)会在各种应用题中,抽象或构造出三角形,标出已知量、未知量,确定解三角形的方法,灵活选用正、余弦定理解之.
(2)搞清利用解斜三角形可解决的各类应用问题的基本图形和相等关系.
(3)理解各种应用问题中的有关名词、术语,如坡角、俯角、仰角、方向角、方位角等.
(4)会利用经纬仪器及皮尺等测量工具进行实地测量,会按照要求写实习报告,会用计算器计算测量结果,提高动手操作能力及数学语言表达能力.求不可到达两点间距离 隔河有两目标A与B但不能到达,在岸边选取相距 km的C、D两点,同时,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内).求两目标A,B之间的距离.分析:由题意作出平面示意图(如右图所示),在四边形ABCD中,需由已知条件求出AB的长.由图形可知,在△ACD与△BCD中,利用正弦定理可求得AC与BC,然后在△ABC中,由余弦定理可求出AB.名师点评:如果涉及解多个三角形的问题,在解题中就应注意解题过程的优化.如求AB的长,也可选择在△ABD中应用余弦定理求解,但此时必须求出AD与BD的长,显然求AD不如求AC容易,另外,本题没有要求取近似值,故不应将写成2.236.变式迁移在某海滨城市附近海面上有一台风,据监测,当前台风中心位于城市O东偏南α角方向300 km的海面P处,并以20 km/h的速度向西偏北45°方向移动,台风侵袭的半径为60 km,并以10 km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?正、余弦定理在追击问题中的应用分析:在解题前必须画出示意图,但应该明确以下几个概念:其一是方位角;其二是沿什么方向追,即按什么方位角航行;其三是最快追上,即应理解为按直线航行,且两船所用时间相等.在此基础上,通过解三角形,即可求出CD的方位角及由C到D所需的航行时间. 在海岸A处,发现北偏东45°方向,距A为( -1) km的B处有一艘走私船.在A处北偏西75°方向,距A为2 km的C处的缉私船奉命以10 km/h的速度追截走私船.此时走私船正以10 km/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.名师点评:解题时应明确,方位角是相对每一点而言的,因此,从这个意义上来说,方位角是一个动态角,在理解题意时,应把方位角看活,否则在理解题意上将可能产生失误.变式训练 2.如右图所示,一缉私艇
在A处发现在北偏东45°方向,
距离12 n mile的海面上有一走
私船C正以10 n mile/h的速度
沿东偏南15°方向逃窜.
缉私艇的速度为14 n mile/h,若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追,求追及所需的时间和α角的正弦值.正、余弦定理的综合运用 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100 m后,又从B点测得斜度为45°,设建筑物的高为50 m,求此山对于地平面的斜度的倾斜角θ.(提示:cos 42.94°= -1)分析:设山对于地平面的斜度的倾斜角∠EAD=θ,这样可在△ABC中利用正弦定理求出BC;再在△BCD中,利用正弦定理得到关于θ的三角函数等式,进而解出θ角.名师点评:解应用题,首先要增强应用数学的意识.解应用题可分两步:第一步,先分析问题,抓住实际问题中的数量关系,将其转化成一般数学问题;第二步,利用所学知识和方法解决这个数学问题,其中的关键在于如何将实际问题数学化,也就是说如何将实际问题等价转化成一个数学问题.变式训练 3.如图所示,某货轮在A处看灯塔B在货轮的北偏东75°,距离为12 n mile,在A处看灯塔C在货轮北偏西30°,距离为8 n mile,货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:(1)A处与D处的距离;(2)灯塔C与D处的距离.祝您学业有成
