初中数学九年级下册北师大最大面积是多少导学案
文档属性
| 名称 | 初中数学九年级下册北师大最大面积是多少导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 79.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-04 16:34:37 | ||
图片预览

文档简介
最大面积是多少导学案
学习目标 掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.
学习重点 本节的重点是应用二次函数解决图形有关的最值问题,这是本书惟一的一种类型,也是二次函数综合题目中常见的一种类型.在二次函数的应用中占有重要的地位,是经常考查的题型,根据图形中的线段之间的关系,与二次函数结合,可解决此类问题.
学习难点 由图中找到二次函数表达式是本节的难点,它常用的有三角形相似,对应线段成比例,面积公式等,应用这些等式往往可以找到二次函数的表达式.
学习过程 批注
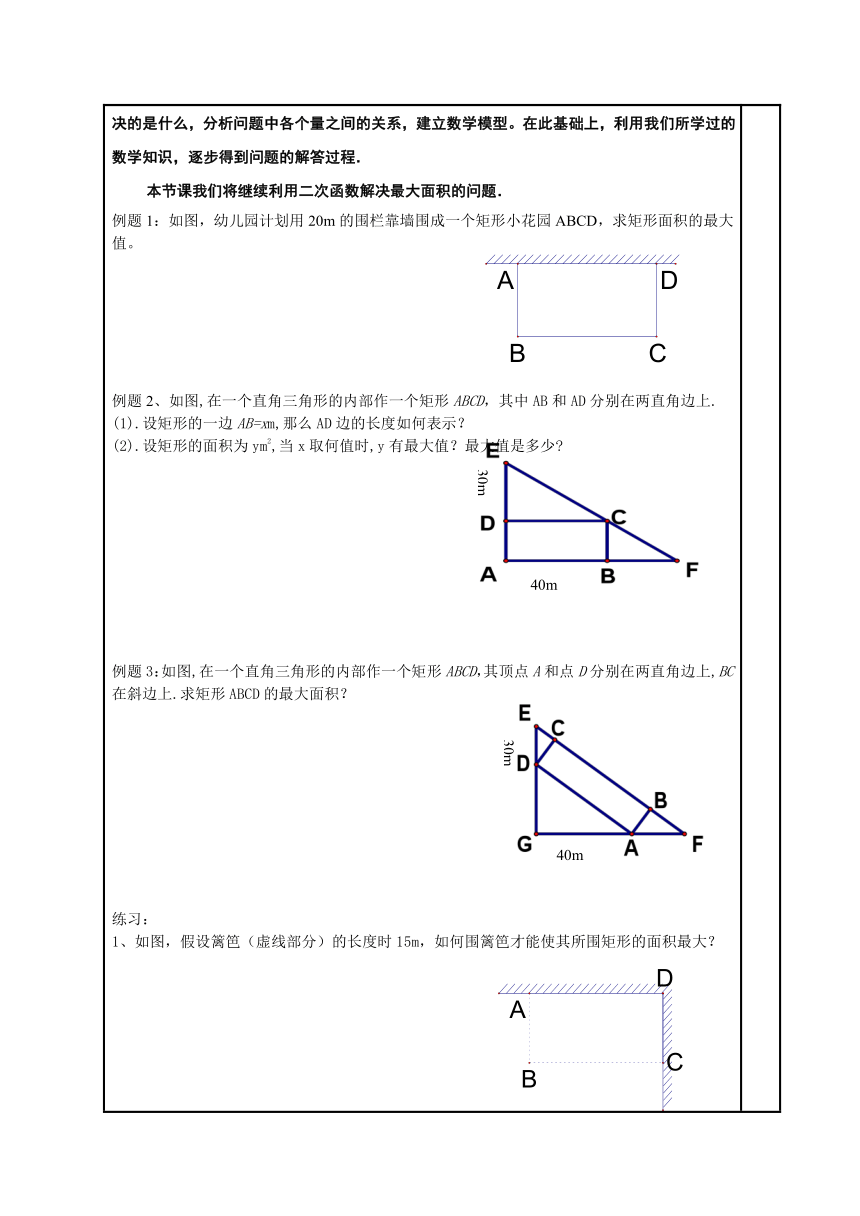
自主学习(课前20分钟)(一)知识回顾1、小强从如图所示的二次函数的图象中,观察得出了下面五条信息:(1);(2) ;(3);(4) ; (5). 你认为其中正确信息的个数有A.2个 B.3个 C.4个 D.5个 2、某商场在销售旺季临近时 ,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的售价为每件20元,并且每周(7天)涨价2元,从第6周开始,保持每件30元的稳定价格销售,直到11周结束,该童装不再销售。 (1)请建立销售价格y(元)与周次x之间的函数关系;(2)若该品牌童装于进货当周售完,且这种童装每件进价z(元)与周次x之间的关系为, 1≤ x ≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?(二)新课预习上节课我们利用二次函数解决了最大利润问题,知道了求最大利润就是求二次函数的最大值,实际上就是利用二次函数来解决实际问题.解决这类问题的关键是要审清题意,明确要解决的是什么,分析问题中各个量之间的关系,建立数学模型。在此基础上,利用我们所学过的数学知识,逐步得到问题的解答过程.本节课我们将继续利用二次函数解决最大面积的问题.例题1:如图,幼儿园计划用20m的围栏靠墙围成一个矩形小花园ABCD,求矩形面积的最大值。例题2、如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.(1).设矩形的一边AB=xm,那么AD边的长度如何表示?(2).设矩形的面积为ym2,当x取何值时,y有最大值?最大值是多少 例题3:如图,在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.求矩形ABCD的最大面积?练习:1、如图,假设篱笆(虚线部分)的长度时15m,如何围篱笆才能使其所围矩形的面积最大?2、把一根长120cm的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积是多少 它们的面积和最小是多少 3、如图,有块三角形土地,它的底边BC=100m,高AH=80m,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,求这个矩形的最大面积?4、如图,△ABC是边长为4的等边三角形,P是BC上一点(点P与B、C不重合),PD∥AC交AB于D,PE∥AB交AC于E,设PB为x,四边形ADPE的面积为y。(1)求y于x的函数关系式(2)求出当x为何值时,y最大,最大值是多少?作业:1.如图1,中,,,点在线段上运动,点、分别在线段、上,且使得四边形是矩形.设的长为,矩形的面积为,已知是的函数,其图象是过点(12,36)的抛物线的一部分(1)求的长;(2)当为何值时,矩形的面积最大,并求出最大值.2.如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米。学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图)。其中矩形EFGH的一边EF在边BC上.其余两个顶点H、G分别在边AB、AC上。现计划在△AHG上种草,每平方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元。(1)当FG长为多少米时,种草的面积与种花的面积相等?(2)当矩形EFGH的边FG为多少米时,△ABC空地改造总投资最小?最小值为多少?(灵活应用二次函数解决生活中最大面积问题)3.正方形边长为4,、分别是、上的两个动点,当点在上运动时,保持和垂直,(1)证明:;(2)设,梯形的面积为,求与之间的函数关系式;当点运动到什么位置时,四边形面积最大,并求出最大面积;
30m
40m
30m
40m
学习目标 掌握长方形和窗户透光最大面积问题,体会数学的模型思想和数学应用价值.学会分析和表示不同背景下实际问题中的变量之间的二次函数关系,并运用二次函数的知识解决实际问题.
学习重点 本节的重点是应用二次函数解决图形有关的最值问题,这是本书惟一的一种类型,也是二次函数综合题目中常见的一种类型.在二次函数的应用中占有重要的地位,是经常考查的题型,根据图形中的线段之间的关系,与二次函数结合,可解决此类问题.
学习难点 由图中找到二次函数表达式是本节的难点,它常用的有三角形相似,对应线段成比例,面积公式等,应用这些等式往往可以找到二次函数的表达式.
学习过程 批注
自主学习(课前20分钟)(一)知识回顾1、小强从如图所示的二次函数的图象中,观察得出了下面五条信息:(1);(2) ;(3);(4) ; (5). 你认为其中正确信息的个数有A.2个 B.3个 C.4个 D.5个 2、某商场在销售旺季临近时 ,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的售价为每件20元,并且每周(7天)涨价2元,从第6周开始,保持每件30元的稳定价格销售,直到11周结束,该童装不再销售。 (1)请建立销售价格y(元)与周次x之间的函数关系;(2)若该品牌童装于进货当周售完,且这种童装每件进价z(元)与周次x之间的关系为, 1≤ x ≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?(二)新课预习上节课我们利用二次函数解决了最大利润问题,知道了求最大利润就是求二次函数的最大值,实际上就是利用二次函数来解决实际问题.解决这类问题的关键是要审清题意,明确要解决的是什么,分析问题中各个量之间的关系,建立数学模型。在此基础上,利用我们所学过的数学知识,逐步得到问题的解答过程.本节课我们将继续利用二次函数解决最大面积的问题.例题1:如图,幼儿园计划用20m的围栏靠墙围成一个矩形小花园ABCD,求矩形面积的最大值。例题2、如图,在一个直角三角形的内部作一个矩形ABCD,其中AB和AD分别在两直角边上.(1).设矩形的一边AB=xm,那么AD边的长度如何表示?(2).设矩形的面积为ym2,当x取何值时,y有最大值?最大值是多少 例题3:如图,在一个直角三角形的内部作一个矩形ABCD,其顶点A和点D分别在两直角边上,BC在斜边上.求矩形ABCD的最大面积?练习:1、如图,假设篱笆(虚线部分)的长度时15m,如何围篱笆才能使其所围矩形的面积最大?2、把一根长120cm的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积是多少 它们的面积和最小是多少 3、如图,有块三角形土地,它的底边BC=100m,高AH=80m,某单位要沿着地边BC修一座底面是矩形DEFG的大楼,求这个矩形的最大面积?4、如图,△ABC是边长为4的等边三角形,P是BC上一点(点P与B、C不重合),PD∥AC交AB于D,PE∥AB交AC于E,设PB为x,四边形ADPE的面积为y。(1)求y于x的函数关系式(2)求出当x为何值时,y最大,最大值是多少?作业:1.如图1,中,,,点在线段上运动,点、分别在线段、上,且使得四边形是矩形.设的长为,矩形的面积为,已知是的函数,其图象是过点(12,36)的抛物线的一部分(1)求的长;(2)当为何值时,矩形的面积最大,并求出最大值.2.如图所示.某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造.已知△ABC的边BC长120米,高AD长80米。学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图)。其中矩形EFGH的一边EF在边BC上.其余两个顶点H、G分别在边AB、AC上。现计划在△AHG上种草,每平方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建爱心鱼池,每平方米投资4元。(1)当FG长为多少米时,种草的面积与种花的面积相等?(2)当矩形EFGH的边FG为多少米时,△ABC空地改造总投资最小?最小值为多少?(灵活应用二次函数解决生活中最大面积问题)3.正方形边长为4,、分别是、上的两个动点,当点在上运动时,保持和垂直,(1)证明:;(2)设,梯形的面积为,求与之间的函数关系式;当点运动到什么位置时,四边形面积最大,并求出最大面积;
30m
40m
30m
40m
