7.4 实践与探索 课件(共31张PPT)
文档属性
| 名称 | 7.4 实践与探索 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-27 00:00:00 | ||
图片预览











文档简介
(共31张PPT)
7.4 实践与探索
华师大版 七年级 下册
教学目标
教学目标:1.能够根据具体的数量关系,列出二元一次方程组解决简单的实
际问题.
2.通过分析实际问题中的数量关系,建立方程解决问题,进一步
认识方程组模型的重要性.
教学重点: 能够根据具体的数量关系,列出二元一次方程组解决简单的实际
问题.
教学难点:通过分析实际问题中的数量关系,建立方程解决问题,进一步认识
方程组模型的重要性.
新知导入
情境引入
列二元一次方程组解决实际问题的步骤是什么?
1、设适当的未知数.(注意单位)
2、根据题意,寻找两个等量关系.
3、根据两个等量关系,列出方程组.
4、解方程组.
5、检验是否符合题意.
6、作答.
(关键)
新知讲解
合作学习
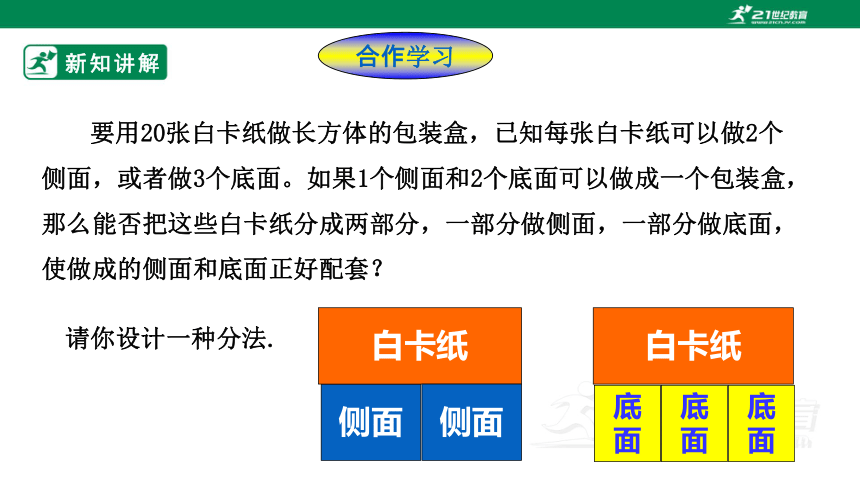
要用20张白卡纸做长方体的包装盒,已知每张白卡纸可以做2个侧面,或者做3个底面。如果1个侧面和2个底面可以做成一个包装盒,那么能否把这些白卡纸分成两部分,一部分做侧面,一部分做底面,使做成的侧面和底面正好配套?
请你设计一种分法.
侧面
白卡纸
侧面
白卡纸
底
面
底
面
底
面
想一想:如果可以将一张白卡纸裁出一个侧面和一个底面,那么,该如何分这些白卡纸,才能既使做出的侧面和底面配套,又能充分利用白卡纸
1.本题中的已知量
(1)共有白卡纸20张。
(2)一张白卡纸可以做2个侧面或3个底面。
(3)1个侧面与2个底面配成一套。
2.从已知中找出两个等量关系.
(1)用做侧面的白卡纸张数+用做底面的白卡纸张数=20
(2)底面的个数是侧面的个数的2倍
3.本题求的量
用几张白卡纸做侧面,几张白卡纸做底面,侧面与底面刚好配套。
设用x张白卡纸做侧面,y张白卡纸做底面。侧面共有2x个,底面共有3y个。
x+y=20
2×2x=3y
1个侧面与2个底面
配成一套
侧面
白卡纸
侧面
白卡纸
底
面
底
面
底
面
通过试验发现:
1张白卡纸能做0个盒子;
2张白卡纸能做1个盒子,1张做盒身,1张做盒底盖;
3张白卡纸能做2个盒子,1张做盒身,2张做盒底盖;
4张白卡纸能做3个盒子,2张做盒身,2张做盒底盖;
5张白卡纸能做4个盒子,2张做盒身,3张做盒底盖;
6张白卡纸能做5个盒子,2张做盒身,4张做盒底盖;
7张白卡纸能做6个盒子,3张做盒身,4张做盒底盖;
第8张和第1张情况类似;
第9张和第2张情况类似------
归纳:用n表示纸的张数.
1.若n=7k+1(k是自然数),情况和1张的情况相同;
2.若n=7k+2(k是自然数),情况和2张的情况相同;
3.若n=7k+6(k是自然数),情况和6张的情况相同;
4.若n=7k (k是自然数),盒子的数量是64k.
20张卡纸,20=7×2+6,余数是6,因此和6张相似,可以做5个盒子,14张纸可以做6×2=12个盒子,因此20张白卡纸可以做17个盒子.
解:设用x张白卡纸做侧面,y张白卡纸做底面。
依题意得
解方程组得
当白卡纸可以套裁时,用8张做侧面,11张做底面,
另一张套裁出1个侧面,1个底面,则共可做盒身17个,
盒底盖34个,正好配成17个包装盒,充分利用了材料.
想一想
如果一张白卡纸可以裁出一个侧面和一个底面,那么,又怎样分这些白卡纸,才能既使做出的侧面和底面配套,又能充分利用白卡纸?
用8张做侧面,11张做底面,另一张裁出1个侧面,1个底面,
则共可做侧面17个,底面34个,正好陪成7个包装盒,较充分利用材料.
提炼概念
列二元一次方程组解应用题的步骤:
1.审题:分析题目中已知量和未知量;
2.设未知数:设未知数,一般设为x,y(要注意单位);
3.找等量关系:找出等量关系;
4.列方程组:根据等量关系列二元一次方程组;
5.解方程组:解二元一次方程组;
6.检验并作答:代入方程组,检验是否符合题意.
典例精讲
例:小明在拼图时,发现8个大小一样的长方形,恰好可以拼成一个大的长方形.小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如下图的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!你能帮他们解开其中的奥秘吗?
小
红
小
明
你能求出这些长方形的长和宽吗?
仔细观察图形 寻找相等关系.
设长方形的长为xmm,宽为ymm.
2
3个长方形的长=5个长方形的宽
即:3x=5y
1个长方形的长+ 2mm =2个长方形的宽
即:x+2=2y
2
2个长方形的长+2mm=一个长方形的长+2个长方形的宽
即:2x+2=x+2y
化简得:2y-x=2
根据题意,得
解得
解:设长方形的长为xmm ,宽为ymm.
答:长方形的长为10mm ,宽为6mm .
2
在6.3节提出的问题中选出一个,用本章的方法来处理,并比较一下两种方法,谈谈你的感受.
做一做
6.3问题1(2)
用一根长60厘米的铁丝围成一个长方形.
(2)如果长方形的宽比长少4厘米,求这个长方形的面积;
解:设长方形长为x厘米,宽为y厘米.
解得
长方形长为17厘米,宽为13厘米,S=13×17=221(平方厘米).
归纳概念
处理问题的过程可以进一步概括为:
课堂练习
B
2.一块长方形菜园,长是宽的3倍,如果长减少3米,宽增加4米,这个长方形就变成一个正方形.设这个长方形菜园的长为x米,宽为y米,根据题意,得( )
C
3. 某加工厂有工人50名,生产某种一个螺栓套两个螺母的配套产品,每人每天平均生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,能使生产出的螺栓和螺母刚好配套?设应安排x人生产螺栓,y人生产螺母,则所列方程组为( )
B
4.某服装厂要生产一批同型号的运动服,已知每3米长的布料可做2件上衣或3条裤子.现有布料300米,请你设计一下,如何分配布料,使运动服成套且不浪费?
5.亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
解:(1)设计划调配36座新能源客车x辆,该大学共有y名志愿者,则需调配22座新能源客车(x+4)辆,
依题意,得:
解得:
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
解:(2)设需调配36座客车m辆,22座客车n辆,
依题意,得:36m+22n=218,
∴n=
又∵m,n均为正整数,
∴
答:需调配36座客车3辆,22座客车5辆.
课堂总结
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
2.这种处理问题的过程可以进一步概括为:
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
7.4 实践与探索
华师大版 七年级 下册
教学目标
教学目标:1.能够根据具体的数量关系,列出二元一次方程组解决简单的实
际问题.
2.通过分析实际问题中的数量关系,建立方程解决问题,进一步
认识方程组模型的重要性.
教学重点: 能够根据具体的数量关系,列出二元一次方程组解决简单的实际
问题.
教学难点:通过分析实际问题中的数量关系,建立方程解决问题,进一步认识
方程组模型的重要性.
新知导入
情境引入
列二元一次方程组解决实际问题的步骤是什么?
1、设适当的未知数.(注意单位)
2、根据题意,寻找两个等量关系.
3、根据两个等量关系,列出方程组.
4、解方程组.
5、检验是否符合题意.
6、作答.
(关键)
新知讲解
合作学习
要用20张白卡纸做长方体的包装盒,已知每张白卡纸可以做2个侧面,或者做3个底面。如果1个侧面和2个底面可以做成一个包装盒,那么能否把这些白卡纸分成两部分,一部分做侧面,一部分做底面,使做成的侧面和底面正好配套?
请你设计一种分法.
侧面
白卡纸
侧面
白卡纸
底
面
底
面
底
面
想一想:如果可以将一张白卡纸裁出一个侧面和一个底面,那么,该如何分这些白卡纸,才能既使做出的侧面和底面配套,又能充分利用白卡纸
1.本题中的已知量
(1)共有白卡纸20张。
(2)一张白卡纸可以做2个侧面或3个底面。
(3)1个侧面与2个底面配成一套。
2.从已知中找出两个等量关系.
(1)用做侧面的白卡纸张数+用做底面的白卡纸张数=20
(2)底面的个数是侧面的个数的2倍
3.本题求的量
用几张白卡纸做侧面,几张白卡纸做底面,侧面与底面刚好配套。
设用x张白卡纸做侧面,y张白卡纸做底面。侧面共有2x个,底面共有3y个。
x+y=20
2×2x=3y
1个侧面与2个底面
配成一套
侧面
白卡纸
侧面
白卡纸
底
面
底
面
底
面
通过试验发现:
1张白卡纸能做0个盒子;
2张白卡纸能做1个盒子,1张做盒身,1张做盒底盖;
3张白卡纸能做2个盒子,1张做盒身,2张做盒底盖;
4张白卡纸能做3个盒子,2张做盒身,2张做盒底盖;
5张白卡纸能做4个盒子,2张做盒身,3张做盒底盖;
6张白卡纸能做5个盒子,2张做盒身,4张做盒底盖;
7张白卡纸能做6个盒子,3张做盒身,4张做盒底盖;
第8张和第1张情况类似;
第9张和第2张情况类似------
归纳:用n表示纸的张数.
1.若n=7k+1(k是自然数),情况和1张的情况相同;
2.若n=7k+2(k是自然数),情况和2张的情况相同;
3.若n=7k+6(k是自然数),情况和6张的情况相同;
4.若n=7k (k是自然数),盒子的数量是64k.
20张卡纸,20=7×2+6,余数是6,因此和6张相似,可以做5个盒子,14张纸可以做6×2=12个盒子,因此20张白卡纸可以做17个盒子.
解:设用x张白卡纸做侧面,y张白卡纸做底面。
依题意得
解方程组得
当白卡纸可以套裁时,用8张做侧面,11张做底面,
另一张套裁出1个侧面,1个底面,则共可做盒身17个,
盒底盖34个,正好配成17个包装盒,充分利用了材料.
想一想
如果一张白卡纸可以裁出一个侧面和一个底面,那么,又怎样分这些白卡纸,才能既使做出的侧面和底面配套,又能充分利用白卡纸?
用8张做侧面,11张做底面,另一张裁出1个侧面,1个底面,
则共可做侧面17个,底面34个,正好陪成7个包装盒,较充分利用材料.
提炼概念
列二元一次方程组解应用题的步骤:
1.审题:分析题目中已知量和未知量;
2.设未知数:设未知数,一般设为x,y(要注意单位);
3.找等量关系:找出等量关系;
4.列方程组:根据等量关系列二元一次方程组;
5.解方程组:解二元一次方程组;
6.检验并作答:代入方程组,检验是否符合题意.
典例精讲
例:小明在拼图时,发现8个大小一样的长方形,恰好可以拼成一个大的长方形.小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如下图的正方形.咳,怎么中间还留下了一个洞,恰好是边长为2mm的小正方形!你能帮他们解开其中的奥秘吗?
小
红
小
明
你能求出这些长方形的长和宽吗?
仔细观察图形 寻找相等关系.
设长方形的长为xmm,宽为ymm.
2
3个长方形的长=5个长方形的宽
即:3x=5y
1个长方形的长+ 2mm =2个长方形的宽
即:x+2=2y
2
2个长方形的长+2mm=一个长方形的长+2个长方形的宽
即:2x+2=x+2y
化简得:2y-x=2
根据题意,得
解得
解:设长方形的长为xmm ,宽为ymm.
答:长方形的长为10mm ,宽为6mm .
2
在6.3节提出的问题中选出一个,用本章的方法来处理,并比较一下两种方法,谈谈你的感受.
做一做
6.3问题1(2)
用一根长60厘米的铁丝围成一个长方形.
(2)如果长方形的宽比长少4厘米,求这个长方形的面积;
解:设长方形长为x厘米,宽为y厘米.
解得
长方形长为17厘米,宽为13厘米,S=13×17=221(平方厘米).
归纳概念
处理问题的过程可以进一步概括为:
课堂练习
B
2.一块长方形菜园,长是宽的3倍,如果长减少3米,宽增加4米,这个长方形就变成一个正方形.设这个长方形菜园的长为x米,宽为y米,根据题意,得( )
C
3. 某加工厂有工人50名,生产某种一个螺栓套两个螺母的配套产品,每人每天平均生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,能使生产出的螺栓和螺母刚好配套?设应安排x人生产螺栓,y人生产螺母,则所列方程组为( )
B
4.某服装厂要生产一批同型号的运动服,已知每3米长的布料可做2件上衣或3条裤子.现有布料300米,请你设计一下,如何分配布料,使运动服成套且不浪费?
5.亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
解:(1)设计划调配36座新能源客车x辆,该大学共有y名志愿者,则需调配22座新能源客车(x+4)辆,
依题意,得:
解得:
答:计划调配36座新能源客车6辆,该大学共有218名志愿者.
解:(2)设需调配36座客车m辆,22座客车n辆,
依题意,得:36m+22n=218,
∴n=
又∵m,n均为正整数,
∴
答:需调配36座客车3辆,22座客车5辆.
课堂总结
1.在很多实际问题中,都存在着一些等量关系,因此我们往往可以借助列方程组的方法来处理这些问题.
2.这种处理问题的过程可以进一步概括为:
3.要注意的是,处理实际问题的方法往往是多种多样的,应根据具体问题灵活选用.
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
