人教版五年级下册数学第一单元观察物体(三)解答题训练(含答案)
文档属性
| 名称 | 人教版五年级下册数学第一单元观察物体(三)解答题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 322.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-28 17:24:04 | ||
图片预览

文档简介
人教版五年级下册数学第一单元观察物体(三)解答题训练
1.数一数,画一画。
(1)上图是由( )个小正方体组成的。
(2)分别画出从正面、上面和右面看到的形状。
2.陈凯同学用每一个边长都为5厘米小正方体摆成如图的图形。
(1)从左面看,他所看到的面积是多少平方厘米?
(2)陈凯同学在原图的基础上继续用这种小正方体摆图形,从前面看,看到的面都正好是一个正方形。他再摆上的小正方体是多少个?请举出一个例子,可以用写算式或者画图的方法说明。
3.(1)下图中一共有( )个小正方体。
(2)在下面画出上图从正面看、左面看、上面看到的图形。
4.观察下图三个立体图形从( )面看到的形状是一样的,并在虚线框中画出这个形状。
5.按要求答题。
(1)从①号物体和②号物体的( )面、( )面看到的图形相同。
(2)从①号物体和②号物体的( )面看到的图形不同。
(3)画出两个物体从前面看到的图形。
6.如图中的网格是边长为1cm的小正方形。
(1)图2是由图1先向右平移( )格,再绕点A按( )时针方向旋转( )°得到的。
(2)在图1中标出点A。
(3)一个由小正方体搭成的几何体,如果从正面和上面看到的都是图1的形状,那么这个几何体的表面积最少是( )cm2。
7.添一个。
(1)从正面看,形状不变,有几种摆法?
(2)从上面看,形状不变,有几种摆法?
(3)从侧面看,形状不变,有几种摆法?
8.已知某立体图形是由若干个棱长为1的小正方体组成的,这个立体图形从三个方向看到的图形如下,每个小正方形的边长都是1,请问这个立体图形是由多少个小正方体组成的?
9.如图所示,要使从上面看到的图形不变:
(1)如果是5个小正方体,可以怎样摆?
(2)如果有6个小正方体,可以有几种不同的摆法?
(3)最少可以摆几个小正方体?
10.用4个同样大小的正方体摆成下面的长方体,按下面的要求再添加一个同样大小的正方体,各有多少种不同的摆法?
(1)从下面看到的仍是,共有( )种不同的摆法。
(2)从侧面看到的是,共有( )种不同的摆法。
(3)从侧面看到的是,共有( )种不同摆法。
(4)从侧面看到的仍是,共有( )种不同摆法。
(5)从上面看到的是,共有( )种摆法。
(6)如果从( )面看到的是,那么它另外两个面分别是什么样的?画出来。
11.如下图所示,要使从上面看到的图形不变:
(1)如果是5个小正方体,可以有几种不同的摆法?
(2)如果有6个小正方体,可以怎样摆?
(3)最多可以摆几个小正方体?
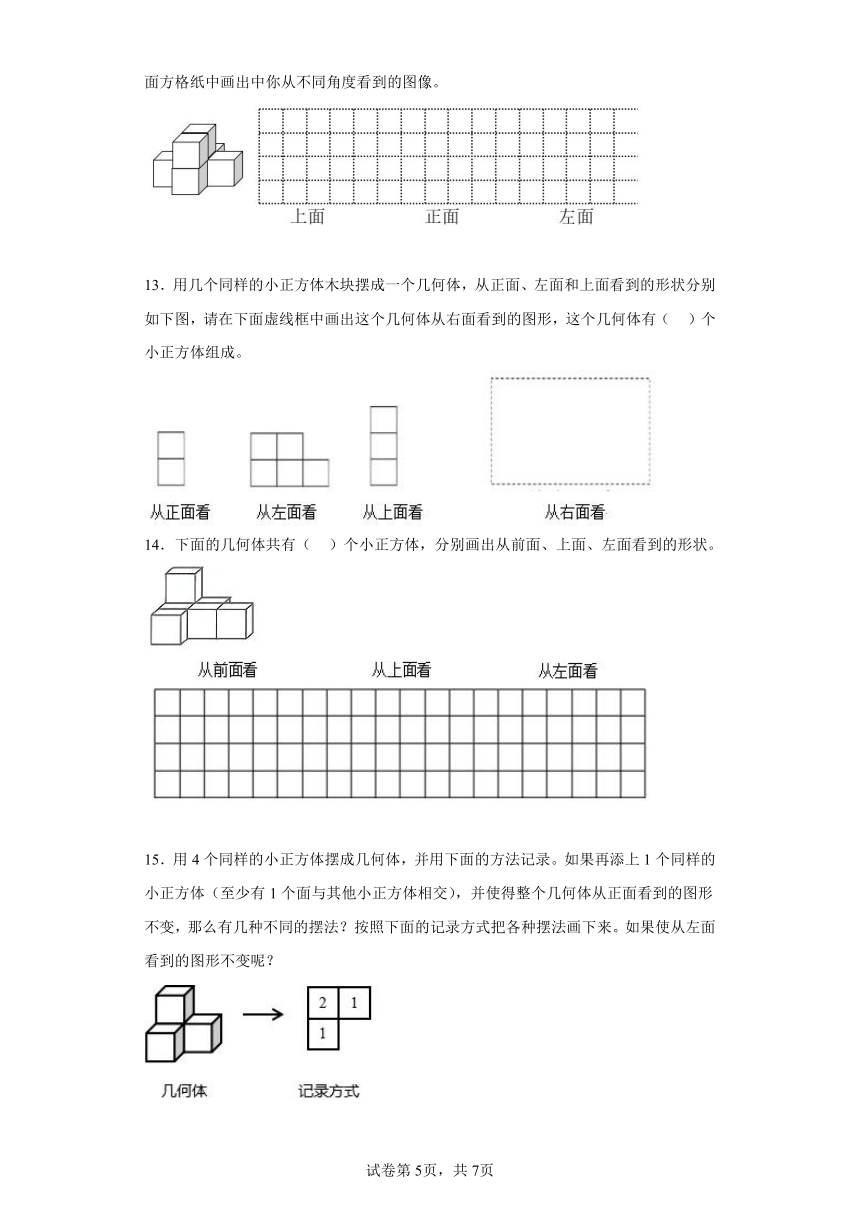
12.下图由( )个小正方体组成,有( )层。它有( )个“□”露在外面。请在下面方格纸中画出中你从不同角度看到的图像。
13.用几个同样的小正方体木块摆成一个几何体,从正面、左面和上面看到的形状分别如下图,请在下面虚线框中画出这个几何体从右面看到的图形,这个几何体有( )个小正方体组成。
14.下面的几何体共有( )个小正方体,分别画出从前面、上面、左面看到的形状。
15.用4个同样的小正方体摆成几何体,并用下面的方法记录。如果再添上1个同样的小正方体(至少有1个面与其他小正方体相交),并使得整个几何体从正面看到的图形不变,那么有几种不同的摆法?按照下面的记录方式把各种摆法画下来。如果使从左面看到的图形不变呢?
从正面看图形不变: 从左面看图形不变:
16.明明摆了一个几何体,从左面和正面看到的图形如下。
聪明的同学们,你知道明明摆这个几何体最少需要多少个小正方体吗?最多呢?
17.如下图所示,要使从上面看到的图形不变。
(1)如果有6个小正方体,有几种不同的摆法?可以怎样摆?
(2)如果有7个小正方体,有几种不同的摆法?说说你的理由。
18.把9个棱长是1 cm的小正方体拼在一起(如下图),从正面看和从左面看,所看到的图形的面积之和是多少 取走几号小正方体后,从上面和左面看到的形状不变
19.搭一个这样的立体图形最少需要几个小正方体?最多可以有几个小正方体?
20.下图是一个由若干个小正方体搭建而成的几何体从正面和左面看到的图形,小刚用小立方体搭建以后,认为下图中的三个图形都可以是该几何体从上面看到的图形,你同意他的看法吗?
21.4个棱长为30厘米的正方体想箱子放在墙角处.
(1)分别画出从正面、右面、上面看到的图形.
(2)共有________个面露在外面,露在外面的面积是________平方厘米.
试卷第6页,共7页
试卷第7页,共7页
参考答案:
1.(1)10
2.(1)75平方厘米
(2)5个
3.(1)6
4.左;
5.(1)上;侧(2)前、后
6.(1)6;逆;90
(3)22
7.(1)8种;
(2)5种;
(3)6种
8.9个
9.(1)(答案不唯一)
(2)(答案不唯一)
(3)4个
10.(1)4;(2)8;(3)4;(4)2;(5)1;
(6)上;;
11.(1)4种
(2)10种
(3)无数个
12.7,2,23
13.5
14.7;
16.最少需要6个同样的小正方体,最多需要11个。
17.(1)有5种不同的摆法(上面的数字表示在这个位置上所用的小正方体的个数)如图:
(2)有15种不同的摆法,理由见解析。
18.11cm2 3号
19.6个;9个
20.同意小刚的看法。
21.(1)
(2)9;8100
答案第2页,共2页
答案第1页,共2页
1.数一数,画一画。
(1)上图是由( )个小正方体组成的。
(2)分别画出从正面、上面和右面看到的形状。
2.陈凯同学用每一个边长都为5厘米小正方体摆成如图的图形。
(1)从左面看,他所看到的面积是多少平方厘米?
(2)陈凯同学在原图的基础上继续用这种小正方体摆图形,从前面看,看到的面都正好是一个正方形。他再摆上的小正方体是多少个?请举出一个例子,可以用写算式或者画图的方法说明。
3.(1)下图中一共有( )个小正方体。
(2)在下面画出上图从正面看、左面看、上面看到的图形。
4.观察下图三个立体图形从( )面看到的形状是一样的,并在虚线框中画出这个形状。
5.按要求答题。
(1)从①号物体和②号物体的( )面、( )面看到的图形相同。
(2)从①号物体和②号物体的( )面看到的图形不同。
(3)画出两个物体从前面看到的图形。
6.如图中的网格是边长为1cm的小正方形。
(1)图2是由图1先向右平移( )格,再绕点A按( )时针方向旋转( )°得到的。
(2)在图1中标出点A。
(3)一个由小正方体搭成的几何体,如果从正面和上面看到的都是图1的形状,那么这个几何体的表面积最少是( )cm2。
7.添一个。
(1)从正面看,形状不变,有几种摆法?
(2)从上面看,形状不变,有几种摆法?
(3)从侧面看,形状不变,有几种摆法?
8.已知某立体图形是由若干个棱长为1的小正方体组成的,这个立体图形从三个方向看到的图形如下,每个小正方形的边长都是1,请问这个立体图形是由多少个小正方体组成的?
9.如图所示,要使从上面看到的图形不变:
(1)如果是5个小正方体,可以怎样摆?
(2)如果有6个小正方体,可以有几种不同的摆法?
(3)最少可以摆几个小正方体?
10.用4个同样大小的正方体摆成下面的长方体,按下面的要求再添加一个同样大小的正方体,各有多少种不同的摆法?
(1)从下面看到的仍是,共有( )种不同的摆法。
(2)从侧面看到的是,共有( )种不同的摆法。
(3)从侧面看到的是,共有( )种不同摆法。
(4)从侧面看到的仍是,共有( )种不同摆法。
(5)从上面看到的是,共有( )种摆法。
(6)如果从( )面看到的是,那么它另外两个面分别是什么样的?画出来。
11.如下图所示,要使从上面看到的图形不变:
(1)如果是5个小正方体,可以有几种不同的摆法?
(2)如果有6个小正方体,可以怎样摆?
(3)最多可以摆几个小正方体?
12.下图由( )个小正方体组成,有( )层。它有( )个“□”露在外面。请在下面方格纸中画出中你从不同角度看到的图像。
13.用几个同样的小正方体木块摆成一个几何体,从正面、左面和上面看到的形状分别如下图,请在下面虚线框中画出这个几何体从右面看到的图形,这个几何体有( )个小正方体组成。
14.下面的几何体共有( )个小正方体,分别画出从前面、上面、左面看到的形状。
15.用4个同样的小正方体摆成几何体,并用下面的方法记录。如果再添上1个同样的小正方体(至少有1个面与其他小正方体相交),并使得整个几何体从正面看到的图形不变,那么有几种不同的摆法?按照下面的记录方式把各种摆法画下来。如果使从左面看到的图形不变呢?
从正面看图形不变: 从左面看图形不变:
16.明明摆了一个几何体,从左面和正面看到的图形如下。
聪明的同学们,你知道明明摆这个几何体最少需要多少个小正方体吗?最多呢?
17.如下图所示,要使从上面看到的图形不变。
(1)如果有6个小正方体,有几种不同的摆法?可以怎样摆?
(2)如果有7个小正方体,有几种不同的摆法?说说你的理由。
18.把9个棱长是1 cm的小正方体拼在一起(如下图),从正面看和从左面看,所看到的图形的面积之和是多少 取走几号小正方体后,从上面和左面看到的形状不变
19.搭一个这样的立体图形最少需要几个小正方体?最多可以有几个小正方体?
20.下图是一个由若干个小正方体搭建而成的几何体从正面和左面看到的图形,小刚用小立方体搭建以后,认为下图中的三个图形都可以是该几何体从上面看到的图形,你同意他的看法吗?
21.4个棱长为30厘米的正方体想箱子放在墙角处.
(1)分别画出从正面、右面、上面看到的图形.
(2)共有________个面露在外面,露在外面的面积是________平方厘米.
试卷第6页,共7页
试卷第7页,共7页
参考答案:
1.(1)10
2.(1)75平方厘米
(2)5个
3.(1)6
4.左;
5.(1)上;侧(2)前、后
6.(1)6;逆;90
(3)22
7.(1)8种;
(2)5种;
(3)6种
8.9个
9.(1)(答案不唯一)
(2)(答案不唯一)
(3)4个
10.(1)4;(2)8;(3)4;(4)2;(5)1;
(6)上;;
11.(1)4种
(2)10种
(3)无数个
12.7,2,23
13.5
14.7;
16.最少需要6个同样的小正方体,最多需要11个。
17.(1)有5种不同的摆法(上面的数字表示在这个位置上所用的小正方体的个数)如图:
(2)有15种不同的摆法,理由见解析。
18.11cm2 3号
19.6个;9个
20.同意小刚的看法。
21.(1)
(2)9;8100
答案第2页,共2页
答案第1页,共2页
