8.1 认识不等式 课件(共27张PPT)
文档属性
| 名称 | 8.1 认识不等式 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-29 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
8.1 认识不等式
华师大版 七年级 下册
教学目标
教学目标:1、了解不等式的意义;
2、经历由具体事列建立不等式模型的过程,进一步发展学生
的符号感与数学化的能力;
3、初步体会不等式是研究量与量之间关系的重要模型之一.
教学重点:不等式的概念及其解的意义.
教学难点:不等式的解的意义.
新知导入
情境引入
中间的“15”是什么意思呢?
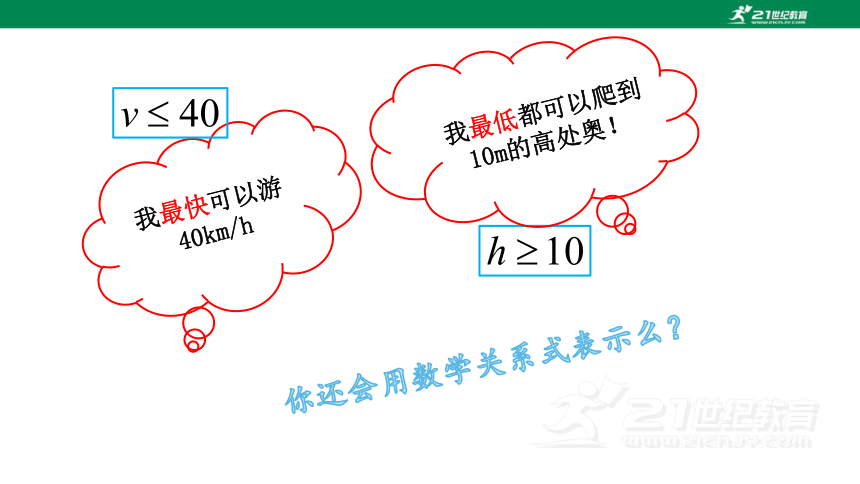
我最快可以游40km/h
你还会用数学关系式表示么?
我最低都可以爬到10m的高处奥!
同学们,小时候玩过翘翘板吗?
左边重,右边轻
左边轻,右边重
新知讲解
合作学习
新知讲解
世纪公园的票价是每人5元;一次购票满30张,每张票可少收1元.某班有27名少先队员去世纪公园进行活动.当领队王小华准备好了零钱到售票处买27张票时,爱动脑筋的李敏同学喊住了王小华,提议买30张票.但有的同学不明白,明明我们只有27个人,买30张票,岂不是“浪费”吗
问题
那么,究竟李敏的提议对不对
是不是真的“浪费”呢
买27张票,要付款5x27 = 135(元).
买30张票,要付款4x30=120(元).
显然 120< 135.
这就是说,买30张票比买27张票付款要少,表面上看是“浪费”了3张票,实际上反而节省了.
解决这个
问题的关键是
比较两种方式
付款的多少.
当然,如果去世纪公园的人数较少(例如10个人),
显然不值得去买30张票,还是按实际人数买票为好.
现在的问题是:少于30人时,有多少人去世纪公园,买30
张票反而合算呢
设有x人要去世纪公园.
如果x<30,那么按实际人数买票x张,要付款5x(元);
买30张票,要付款4×30=120(元).
如果买30张票合算,那么应有120 < 5x.
现在的问题就是:x取哪些数值时,上式成立
前面已经算过,当x=27时,上式成立.
探索
尝试、检验,
找出符合要求的答案.
x 5x 比较120与5x的大小 120<5x成立吗?
21 105 120>5x 不成立
22
23
24
25
26
27 135 120<5x 成立
28
29
让我们再取一些值试一试,将结果填入下表
110
115
120
125
130
140
145
120>5x
120>5x
120>5x
120<5x
120<5x
120<5x
120<5x
不成立
不成立
不成立
成立
成立
成立
成立
由上表可见,当x=____________时,120<5x成立.
也就是说,少于30人时,至少要有________人进公园,
买30张票反而合算.
25,26,…
25
提炼概念
像上面出现的120<135, x<30, 120< 5x那样用不等号“<”或“>”表示不等关系的式子,叫做不等式( inequality).
像“>”“<”“≥”“≤”“ ≠”这样的符号统称为不等号.“≥”、“≤”也表示不等,前者表示“不小于”(大于或等于),后者表示“不大于”(小于或等于).
“≠”表示左右两边不相等.
概括
不等式120 <5x中含有未知数x.能使不等式成立的未知数的值,叫做不等式的解( solution of inequality).
如上例中,x = 25, 26, 27, ...都是不等式120<5x的解,而x=24,23,22,21则都不是它的解.
典例精讲
例 用不等式表示下列关系,并分别写出两个满足不等式的数:
(1) x的一半小于-1;
(2) y与4的和大于0.5;
(3) a负数;
(4)b是非负数
解:
(1) <- 1.如x=-3,-4.
(2)y+4>0.5.如y=0,1.
(3)a<0.如a=-3,-4.
(4)b是非负数,即b不是负数,所以b>0或b=0.
如b =0, 2.
b>0或b=0,
通常可表示成b≥0.
变式 判断下列各式哪些是等式,哪些不是等式;若不是,请说明理由.
(1)2x+3×4=17
(2)S=ab
(3)a(b+c)=ab+ac
(4)2x-2y
(5)3x=2x+7
(6)2 < 3
解:(1)(2)(3)(5)是等式;
(4)不是等式,因为没有等号,是代数式;
(6)不是等式,是不等式.
归纳概念
列不等式的一般步骤是:
(1)分析题意,找出题目中的各种量;
(2)寻找各种量之间的不等关系;
(3)用代数式表示各量
(4)用适当的符号将各量连接起来
课堂练习
1.下列式子:① 3x = 5;② a>2;③ 3m – 1 ≤ 4;④ 5x + 6y;⑤ – 1>2中. 不等式有( )个.
A.2 B.3 C.4 D.5
B
2.下列式子:(1)4>0;(2)2x+3y<0;(3)x=3;(4)x≠y;(5)x+y;(6)x+3≤7中,不等式的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
C
3.填空:
(1)小于等于4的正整数有( )
(2) 绝对值小于3的负整数的和为( )
(3) 绝对值不大于3的整数有( )
(4)不等式3x-5<1的解且x的绝对值小于3的整数有( )
1、2、3
-3
-3、-2、-1、0、1、2、3
-2、-1、0、1
4.用不等式表示:
(1)a的5倍与3的和大于5;
(2)x的3倍与1的差小于2;
(3)a的2倍与1的差是正数;
(4)m与2的差是负数.
解:(1)5a+3>5.
(2)3x-1<2.
(3)2a-1>0.
(4)m-2<0.
5.按下列条件,写出不等式.
(1)-1<3,两边都加上1;
(2)2x>x+1,两边都减去x.
解:(1)∵-1<3,
∴-1+1<3+1,
∴0<4;
(2)∵2x>x+1,
∴2x-x>x+1-x,
∴x>1.
课堂总结
知识总结 知识方法要点 关键总结 注意事项
不等式的概念 表示不等关系的式子 注意“不大于”“不小于”的含义
列不等式 理清要比较的两个量;正确使用不等号 弄清题意,抓住关键词
不等式的解 能使不等式成立的未知数的值 指未知数的某个值
方法规律总结 (1)列不等式可类比列万程的方法,一般先找出要对比的两个量,并表示出来(包括设未知数).再找出表达关系的关键词,用相应的不等符号表示出来,最后连接成不等式. (2)一般地,一个不等式的解不止一个,往往有多个,甚至有无数个 . 作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
8.1 认识不等式
华师大版 七年级 下册
教学目标
教学目标:1、了解不等式的意义;
2、经历由具体事列建立不等式模型的过程,进一步发展学生
的符号感与数学化的能力;
3、初步体会不等式是研究量与量之间关系的重要模型之一.
教学重点:不等式的概念及其解的意义.
教学难点:不等式的解的意义.
新知导入
情境引入
中间的“15”是什么意思呢?
我最快可以游40km/h
你还会用数学关系式表示么?
我最低都可以爬到10m的高处奥!
同学们,小时候玩过翘翘板吗?
左边重,右边轻
左边轻,右边重
新知讲解
合作学习
新知讲解
世纪公园的票价是每人5元;一次购票满30张,每张票可少收1元.某班有27名少先队员去世纪公园进行活动.当领队王小华准备好了零钱到售票处买27张票时,爱动脑筋的李敏同学喊住了王小华,提议买30张票.但有的同学不明白,明明我们只有27个人,买30张票,岂不是“浪费”吗
问题
那么,究竟李敏的提议对不对
是不是真的“浪费”呢
买27张票,要付款5x27 = 135(元).
买30张票,要付款4x30=120(元).
显然 120< 135.
这就是说,买30张票比买27张票付款要少,表面上看是“浪费”了3张票,实际上反而节省了.
解决这个
问题的关键是
比较两种方式
付款的多少.
当然,如果去世纪公园的人数较少(例如10个人),
显然不值得去买30张票,还是按实际人数买票为好.
现在的问题是:少于30人时,有多少人去世纪公园,买30
张票反而合算呢
设有x人要去世纪公园.
如果x<30,那么按实际人数买票x张,要付款5x(元);
买30张票,要付款4×30=120(元).
如果买30张票合算,那么应有120 < 5x.
现在的问题就是:x取哪些数值时,上式成立
前面已经算过,当x=27时,上式成立.
探索
尝试、检验,
找出符合要求的答案.
x 5x 比较120与5x的大小 120<5x成立吗?
21 105 120>5x 不成立
22
23
24
25
26
27 135 120<5x 成立
28
29
让我们再取一些值试一试,将结果填入下表
110
115
120
125
130
140
145
120>5x
120>5x
120>5x
120<5x
120<5x
120<5x
120<5x
不成立
不成立
不成立
成立
成立
成立
成立
由上表可见,当x=____________时,120<5x成立.
也就是说,少于30人时,至少要有________人进公园,
买30张票反而合算.
25,26,…
25
提炼概念
像上面出现的120<135, x<30, 120< 5x那样用不等号“<”或“>”表示不等关系的式子,叫做不等式( inequality).
像“>”“<”“≥”“≤”“ ≠”这样的符号统称为不等号.“≥”、“≤”也表示不等,前者表示“不小于”(大于或等于),后者表示“不大于”(小于或等于).
“≠”表示左右两边不相等.
概括
不等式120 <5x中含有未知数x.能使不等式成立的未知数的值,叫做不等式的解( solution of inequality).
如上例中,x = 25, 26, 27, ...都是不等式120<5x的解,而x=24,23,22,21则都不是它的解.
典例精讲
例 用不等式表示下列关系,并分别写出两个满足不等式的数:
(1) x的一半小于-1;
(2) y与4的和大于0.5;
(3) a负数;
(4)b是非负数
解:
(1) <- 1.如x=-3,-4.
(2)y+4>0.5.如y=0,1.
(3)a<0.如a=-3,-4.
(4)b是非负数,即b不是负数,所以b>0或b=0.
如b =0, 2.
b>0或b=0,
通常可表示成b≥0.
变式 判断下列各式哪些是等式,哪些不是等式;若不是,请说明理由.
(1)2x+3×4=17
(2)S=ab
(3)a(b+c)=ab+ac
(4)2x-2y
(5)3x=2x+7
(6)2 < 3
解:(1)(2)(3)(5)是等式;
(4)不是等式,因为没有等号,是代数式;
(6)不是等式,是不等式.
归纳概念
列不等式的一般步骤是:
(1)分析题意,找出题目中的各种量;
(2)寻找各种量之间的不等关系;
(3)用代数式表示各量
(4)用适当的符号将各量连接起来
课堂练习
1.下列式子:① 3x = 5;② a>2;③ 3m – 1 ≤ 4;④ 5x + 6y;⑤ – 1>2中. 不等式有( )个.
A.2 B.3 C.4 D.5
B
2.下列式子:(1)4>0;(2)2x+3y<0;(3)x=3;(4)x≠y;(5)x+y;(6)x+3≤7中,不等式的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
C
3.填空:
(1)小于等于4的正整数有( )
(2) 绝对值小于3的负整数的和为( )
(3) 绝对值不大于3的整数有( )
(4)不等式3x-5<1的解且x的绝对值小于3的整数有( )
1、2、3
-3
-3、-2、-1、0、1、2、3
-2、-1、0、1
4.用不等式表示:
(1)a的5倍与3的和大于5;
(2)x的3倍与1的差小于2;
(3)a的2倍与1的差是正数;
(4)m与2的差是负数.
解:(1)5a+3>5.
(2)3x-1<2.
(3)2a-1>0.
(4)m-2<0.
5.按下列条件,写出不等式.
(1)-1<3,两边都加上1;
(2)2x>x+1,两边都减去x.
解:(1)∵-1<3,
∴-1+1<3+1,
∴0<4;
(2)∵2x>x+1,
∴2x-x>x+1-x,
∴x>1.
课堂总结
知识总结 知识方法要点 关键总结 注意事项
不等式的概念 表示不等关系的式子 注意“不大于”“不小于”的含义
列不等式 理清要比较的两个量;正确使用不等号 弄清题意,抓住关键词
不等式的解 能使不等式成立的未知数的值 指未知数的某个值
方法规律总结 (1)列不等式可类比列万程的方法,一般先找出要对比的两个量,并表示出来(包括设未知数).再找出表达关系的关键词,用相应的不等符号表示出来,最后连接成不等式. (2)一般地,一个不等式的解不止一个,往往有多个,甚至有无数个 . 作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
