对称与对称变换[下学期]
图片预览


文档简介
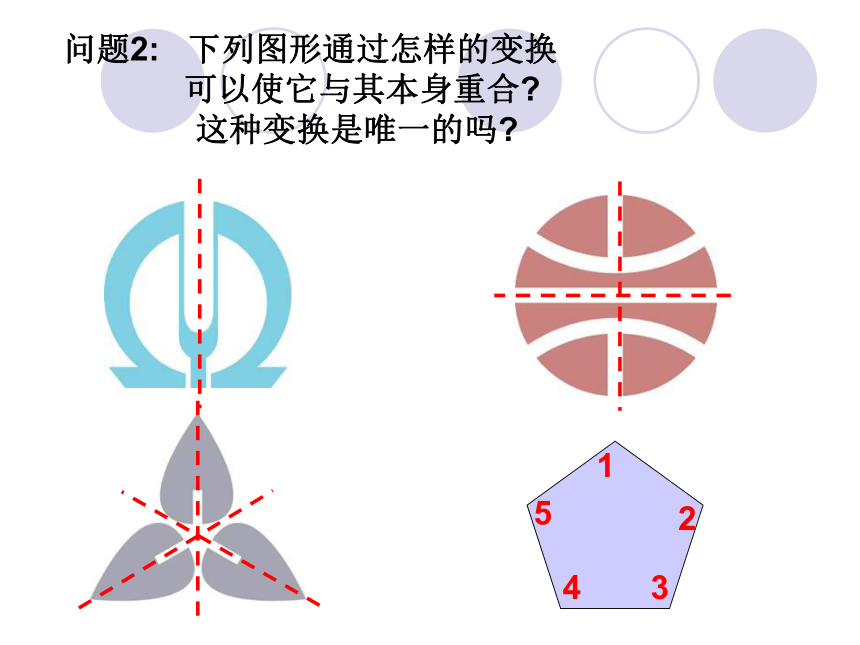
课件19张PPT。埃菲尔铁塔 泰姬陵罗马大教堂 马来西亚双塔 对称就是物体相同部分有规律的重复。 问题1: 什么是对称? 一. 对称 对称与对称变换 问题2: 下列图形通过怎样的变换
可以使它与其本身重合?
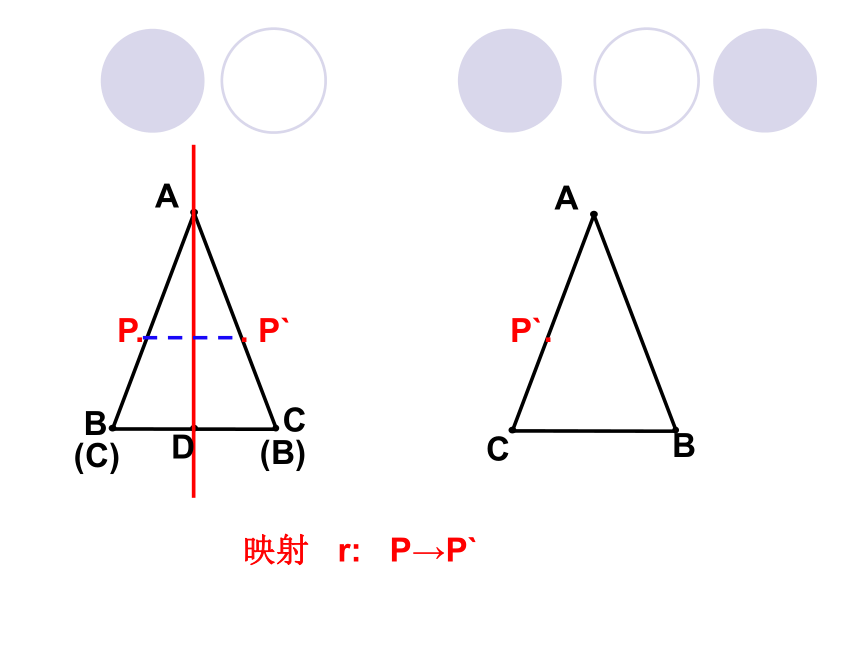
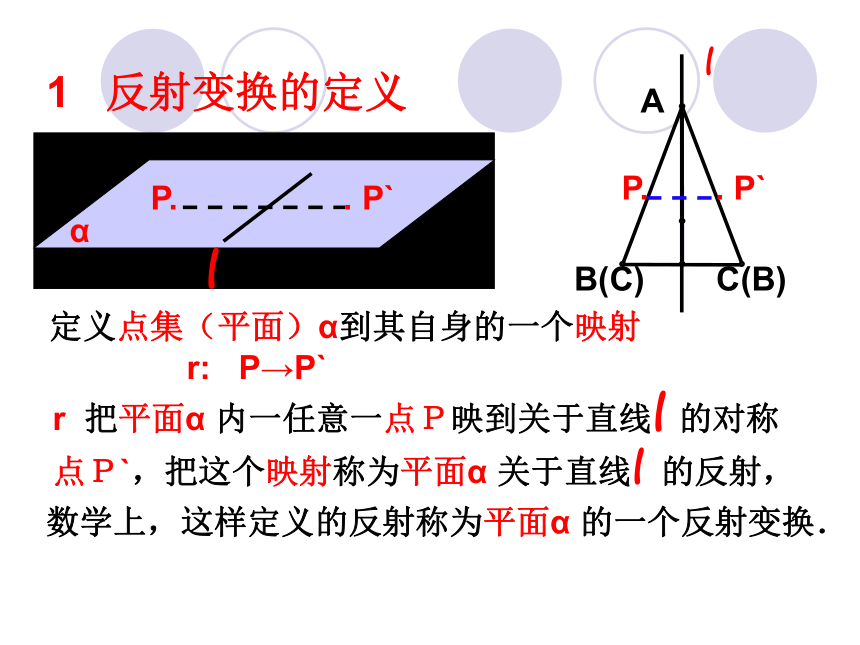
这种变换是唯一的吗?A BCP. . P`D 映射 r: P→P` 1 反射变换的定义 P. . P` l α定义点集(平面)α到其自身的一个映射 r: P→P` r 把平面α 内一任意一点P映到关于直线l 的对称
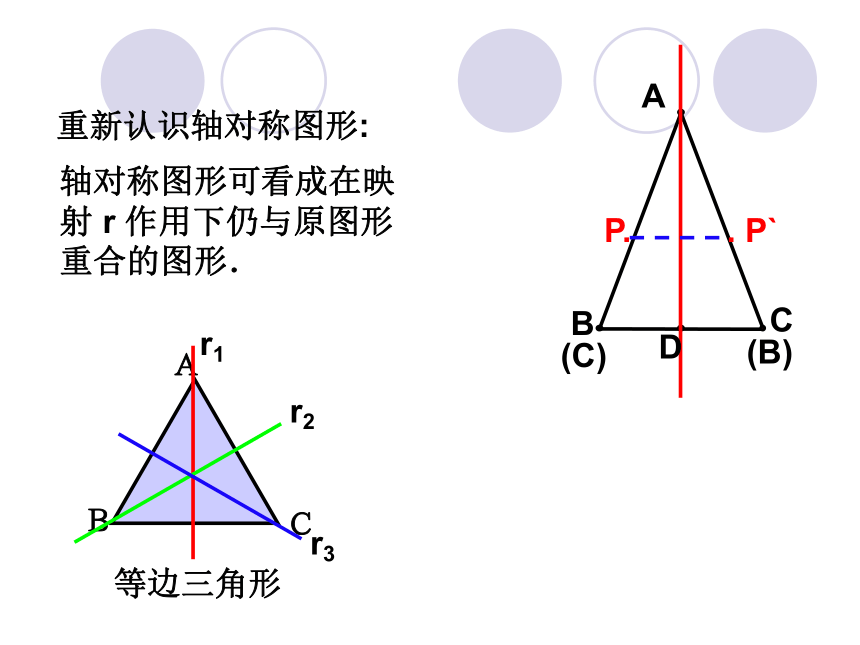
点P`,把这个映射称为平面α 关于直线l 的反射, 数学上,这样定义的反射称为平面α 的一个反射变换. 重新认识轴对称图形: 轴对称图形可看成在映
射 r 作用下仍与原图形
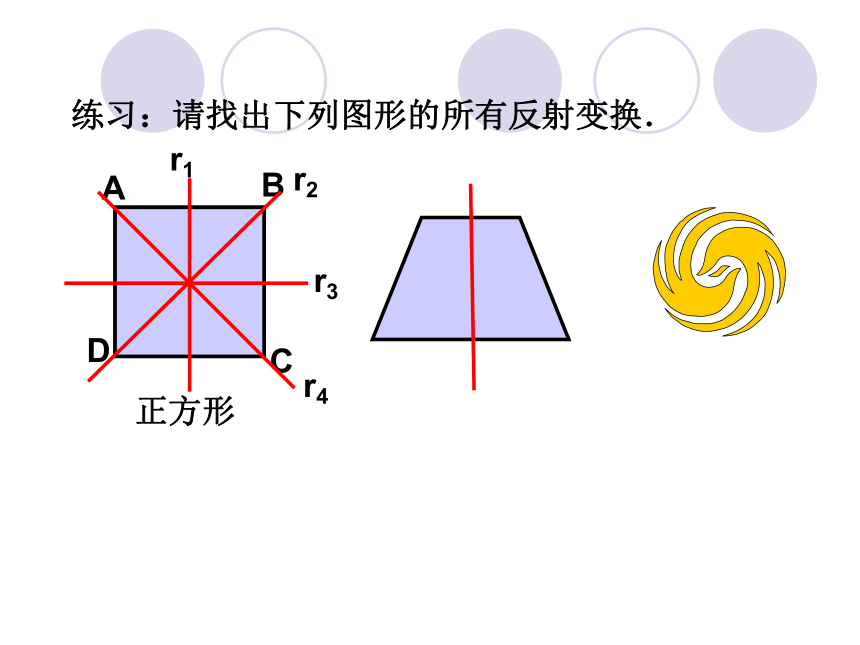
重合的图形.A BCD 练习:请找出下列图形的所有反射变换. 正方形 A C D r2旋转180o.oP. . P` . αO设α是一个平面内所有点构成的集合,O是平面α
内的一个固定点,定义点集(平面)α到其自身的
一个映射ρ: P→P` ρ把平面α内的任意一点P绕点O旋转180o后映
到点P`,这个映射称为以点O为中心转180o的
旋转变换. 这个旋转变换也叫中心对称变换. 2 旋转变换 .o2 旋转变换 设α是一个平面内所有点构成的集合,O是平面α
内的一个固定点,定义点集(平面)α到其自身的
一个映射ρ: P→P` ρ把平面α内的任意一点P绕点O旋转180o后映
到点P`,这个映射称为以点O为中心转180o的
旋转变换. P. . P` . αO加以推广,若以固定点O为中心转任意角(θ<360o)
的旋转, 这样定义的映射数学上叫作旋转变换.特别的当旋转角为0o时,旋转变换叫作恒等变换, 记为I. .oPP`QQ`N..OPP`Q`Q问题: P,Q 是平面内任意两点, 在旋转(或反射)变换
的作用下, 它们的对应点分别是P`,Q`. P`,Q`的
距离与P到Q的距离有什么关系?3 反射变换与旋转变换中的不变性 4. 平面刚体运动 定义:设α是一个平面,映射m: 平面α→平面α是一个一一映射,若m保持平面α内任意
两点间的距离不变,则称m是一个平面刚
体运动。平面刚体运动的性质: 保持距离不变. P. . P` l αQ.. Q`Q.. Q`下列哪些变换是平面刚体运动? .O放大2倍的变换 l l 以直线 l 为轴的反射变换 以点O旋转72o
的变换5. 探求下列图形的所有对称变换 等腰三角形 反射变换: r
恒等变换: I231正三角形 反射变换:
r1, r2, r3 旋转变换:
ρ1, ρ2. 恒等变换:I 正三角形的对称变换记作:
D3={r1, r2, r3, ρ1, ρ2, I } D2={ r, I }正方形的对称变换: 反射变换:
r1, r2, r3 ,r4 旋转变换: ρ1, ρ2, ρ3恒等变换:I正方形的对称变换记作:
D4={r1, r2, r3,r4 , ρ1, ρ2, ρ3 , I } 练习: 请找出下列图形的对称变换 正五边形 正六边形 小 结: 1. 什么是对称? 对称变换 反射变换 旋转变换 3. 平面刚体运动定义及性质 2. 4. 正多边形的对称变换 作业: 1. 请说出下列图形均是什么对称图形,
并找出下列图形的所有对称变换. 作业2: 请探究正n边形的对称变换
可以使它与其本身重合?
这种变换是唯一的吗?A BCP. . P`D 映射 r: P→P` 1 反射变换的定义 P. . P` l α定义点集(平面)α到其自身的一个映射 r: P→P` r 把平面α 内一任意一点P映到关于直线l 的对称
点P`,把这个映射称为平面α 关于直线l 的反射, 数学上,这样定义的反射称为平面α 的一个反射变换. 重新认识轴对称图形: 轴对称图形可看成在映
射 r 作用下仍与原图形
重合的图形.A BCD 练习:请找出下列图形的所有反射变换. 正方形 A C D r2旋转180o.oP. . P` . αO设α是一个平面内所有点构成的集合,O是平面α
内的一个固定点,定义点集(平面)α到其自身的
一个映射ρ: P→P` ρ把平面α内的任意一点P绕点O旋转180o后映
到点P`,这个映射称为以点O为中心转180o的
旋转变换. 这个旋转变换也叫中心对称变换. 2 旋转变换 .o2 旋转变换 设α是一个平面内所有点构成的集合,O是平面α
内的一个固定点,定义点集(平面)α到其自身的
一个映射ρ: P→P` ρ把平面α内的任意一点P绕点O旋转180o后映
到点P`,这个映射称为以点O为中心转180o的
旋转变换. P. . P` . αO加以推广,若以固定点O为中心转任意角(θ<360o)
的旋转, 这样定义的映射数学上叫作旋转变换.特别的当旋转角为0o时,旋转变换叫作恒等变换, 记为I. .oPP`QQ`N..OPP`Q`Q问题: P,Q 是平面内任意两点, 在旋转(或反射)变换
的作用下, 它们的对应点分别是P`,Q`. P`,Q`的
距离与P到Q的距离有什么关系?3 反射变换与旋转变换中的不变性 4. 平面刚体运动 定义:设α是一个平面,映射m: 平面α→平面α是一个一一映射,若m保持平面α内任意
两点间的距离不变,则称m是一个平面刚
体运动。平面刚体运动的性质: 保持距离不变. P. . P` l αQ.. Q`Q.. Q`下列哪些变换是平面刚体运动? .O放大2倍的变换 l l 以直线 l 为轴的反射变换 以点O旋转72o
的变换5. 探求下列图形的所有对称变换 等腰三角形 反射变换: r
恒等变换: I231正三角形 反射变换:
r1, r2, r3 旋转变换:
ρ1, ρ2. 恒等变换:I 正三角形的对称变换记作:
D3={r1, r2, r3, ρ1, ρ2, I } D2={ r, I }正方形的对称变换: 反射变换:
r1, r2, r3 ,r4 旋转变换: ρ1, ρ2, ρ3恒等变换:I正方形的对称变换记作:
D4={r1, r2, r3,r4 , ρ1, ρ2, ρ3 , I } 练习: 请找出下列图形的对称变换 正五边形 正六边形 小 结: 1. 什么是对称? 对称变换 反射变换 旋转变换 3. 平面刚体运动定义及性质 2. 4. 正多边形的对称变换 作业: 1. 请说出下列图形均是什么对称图形,
并找出下列图形的所有对称变换. 作业2: 请探究正n边形的对称变换
