2014届高考物理三轮复习简易通(新课标)三级排查大提分配套课件:专题四 曲线运动(共41张PPT)
文档属性
| 名称 | 2014届高考物理三轮复习简易通(新课标)三级排查大提分配套课件:专题四 曲线运动(共41张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 587.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 物理 | ||
| 更新时间 | 2014-03-05 00:00:00 | ||
图片预览


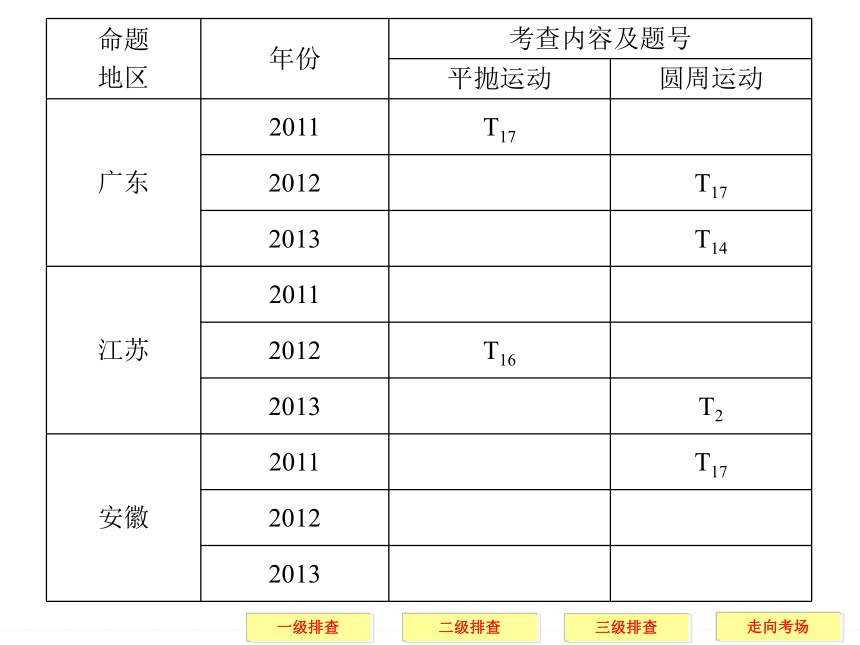
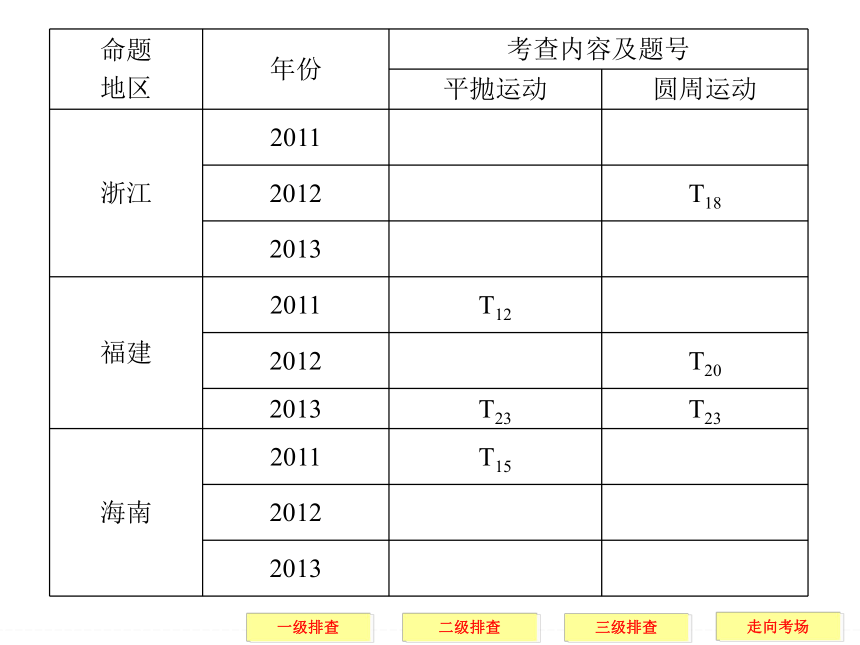








文档简介
课件41张PPT。专题四 曲线运动 说明:以下物理概念、规律的叙述中,在后面的( )内正确的打“√”,错误的打“×”.
1.运动的合成和分解就是几个速度的数字相加减. ( )
2.以水平初速度抛出的物体,只受重力作用下的运动,叫平抛运动,它是匀变速曲线运动. ( )7.做圆周运动的物体所受的合力一定指向圆心,叫做向心力. ( )
8.做圆周运动的物体,当向心力突然消失或向心力不足时,物体做远离圆心的运动,这种现象叫做离心现象. ( )
9.物体做曲线运动的条件:如果物体所受合外力的方向跟物体的速度方向不在一条直线上时,物体就做曲线运动. ( )答案 1.×(订正:进行运动合成和分解时,速度、加速度、位移都是矢量,遵守平行四边形定则) 2.√ 3.√
4.√ 5.√ 6.√ 7.×(订正:做匀速圆周运动的物体,所受的合外力一定指向圆心,产生向心加速度,这种力叫向心力) 8.√ 9.√ 10.√1.物体做曲线运动的条件和特点各是什么?物体做曲线运动时速度的方向、加速度(合外力)的方向、运动轨迹三者是怎样的关系?
提示:(1)物体做曲线运动的条件
物体所受合外力(或加速度)的方向与物体的速度方向不在同一条直线上.
(2)物体做曲线运动的特点
①运动质点在某一点的瞬时速度方向,就是通过这一点的曲线的切线方向.②曲线运动是变速运动,这是因为曲线运动的速度方向是不断变化的.
③做曲线运动的质点,其所受的合外力一定不为零,一定具有加速度.
(3)速度的方向、加速度(合外力)的方向、运动轨迹三者的关系是:质点的运动轨迹夹在速度方向与加速度(合外力)方向之间,且速度方向沿轨迹这一点切线方向、加速度(合外力)方向指向轨迹的凹侧.
易错:不能准确判断曲线运动速度方向、加速度(合外力)方向、轨迹三者之间的关系.2.研究曲线运动的基本方法是——运动的合成与分解,它应用了运动的哪些性质?
提示:运动的合成与分解应用了合运动与分运动的以下性质
①等时性
合运动和分运动经历的时间相等,即同时开始,同时进行,同时停止.
②独立性
一个物体同时参与几个分运动,各分运动独立进行,不受其他运动的影响.③等效性
各分运动的规律叠加起来与合运动的规律有完全相同的效果.
④运动的矢量性:加速度、速度、位移都是矢量,其合成与分解遵循平行四边形定则.
易混:混淆运动的分解与力的分解方法.3.对于匀变速曲线运动问题处理的基本思路是“化曲为直”,具体应如何分解?平抛运动问题处理的基本方法也是分解速度和位移,如何求解平抛运动的合速度及合位移?
提示:(1)匀变速曲线运动的分解方法是沿恒力方向和垂直恒力方向分解,沿垂直恒力方向上做匀速直线运动,沿恒力方向上做匀加速直线运动,这种观点是研究匀变速曲线运动的理论基础,这种观点是力的独立作用原理的体现.易混:混淆θ与α的关系,认为θ=α或θ=2α.4.物体做圆周运动的原因是什么?向心力与物体所受的合力是一回事吗?
提示:力是改变物体运动状态的原因.物体之所以做圆周运动,是因为它受到向心力的作用.向心力是沿与速度垂直方向上所有力的合力,但不一定是物体所受合力,仅当物体做匀速圆周运动时,物体所受向心力由合力提供.
在匀速圆周运动中,由于物体运动的速率不变,动能不变,故物体所受合力与速度时刻垂直、不做功,其方向指向圆心,产生向心加速度,只改变速度的方向.在变速圆周运动中,由于物体运动的速率在改变,动能在改变,故物体受到的合力不指向圆心,即与速度不垂直,合力要做功.合力沿半径方向的分力充当向心力,产生向心加速度,改变速度的方向;合力沿切线方向的分力产生切向加速度,改变速度的大小.
误区:误认为向心力是性质力,受力分析时认为向心力是物体实际受到的力.
易错:变速圆周运动中把物体所受的合力当作向心力.5.圆周运动的动力学问题的解题思路是什么?
易错:不能利用几何关系确定轨道半径.6.物体做匀速圆周运动的条件有哪些?什么条件下物体做向心运动?什么条件下物体做离心运动?
陷阱:物体做离心运动要受到离心力的作用.7.如图1所示,没有物体支撑的小球,例如绳子拴小球、小球在环形轨道的内侧,在竖直平面内做圆周运动.试分析小球能通过最高点的临界条件.图1 易错:找不准小球能通过最高点的临界条件,v>0,就认为小球能在竖直平面内做完整的圆周运动.8.如图2所示,有物体支撑的小球在竖直平面内做圆周运动过最高点的情况:(例如,硬杆、弯管、汽车过拱桥等)
试分析小球能做完整圆周运动的临界条件是什么?并分析在最高点杆对球的作用力的方向.图2 ①当小球通过最高点的速度v=v0时,小球的重力刚好提供做圆周运动的向心力;
②当小球通过最高点的速度v③当小球通过最高点的速度v>v0时,小球通过最高点时,杆对小球有向下的拉力.
易失分:不能正确使用假设法分析求解小球在最高点的受力情况. 猜想一 对运动的合成与分解的考查
命题依据:该考点虽然近几年不是高考的高频考点,但它却是一个较重要的考点,可从不同角度、背景考查考生对曲线运动的处理能力,下面设计的考题是小船渡河问题,是典型的运动合成与分解问题.从过河的最短位移这个角度进行考查,是明年高考重要的考点.试题设计
1.一条船要在最短时间内渡过宽为100 m的河,已知河水的速度v1与船离河岸的距离x的关系如图3甲所示,船在静水中的速度v2与时间t的关系如图乙所示.图3 则以下判断中正确的是 ( ).
A.船渡河的最短时间为25 s
B.船运动的轨迹可能是直线
C.船在河水中航行的加速度大小为a=0.4 m/s2
D.船在河水中的最大速度是5 m/s答案 C猜想二 对平抛运动的考查
命题依据:分析近三年的高考试题,对平抛运动的理解与应用是高考必考内容,为高考的高频考点,主要考查平抛运动规律的应用.下面设计的考题是已知平抛运动某时刻运动的方向,来求解其他物理量,具有预测性.试题设计
2.如图4所示,从某高度水平抛出一小球,经过时间t到达地面时,速度与水平方向的夹角为θ,不计空气阻力,重力加速度为g.下列说法正确的是 ( ).图4 答案 D猜想三 对圆周运动动力学的考查
命题依据:近几年高考中对圆周运动单独考查的试题不多,但圆周运动是高中物理中三种典型运动之一,预测明年可从一个新的角度进行考查.下面设计的考题总以小球在光滑水平面上做半径突变的圆周运动为背景分析细线的拉力F随时间t的变化图象,具有一定的创新性和预测性.试题设计
3.如图5所示,在光滑的水平面上固定两个直立的小铁钉,相距l,长为3l不可伸长的轻质细线一端固定在右侧铁钉上,另一端拴着一个小钢珠,将细线拉直,使小钢珠与两铁钉位于同一直线上.小钢珠以一定的初速度垂直于纸面从图示位置开始运动并开始计时,在小钢珠与铁钉碰撞前,细线拉力F随时间t的变化图象应是 ( ).图5 答案 B 猜想四 对圆周运动与抛体运动相结合的考查
命题依据:近几年高考中对圆周运动与抛体运动、天体运动、动能定理、机械能守恒定律、功能关系相结合的考查较为频繁.预计2014年会重点考查.例:水平面内的圆周运动与平抛运动相结合,竖直平面内的圆周运动与平抛运动相结合等.下面设计的考题为新情景的直线运动,竖直平面内的圆周运动与平抛运动相结合的问题,该题综合性强,为一较好的预测题.试题设计
4.如图6所示,一质量为m=1 kg的小物块轻轻放在水平匀速运动的传送带上的A点,随传送带运动到B点,小物块从C点沿圆弧切线进入竖直光滑的半圆轨道恰能做圆周运动,已知圆弧半径R=0.9 m,轨道最低点为D,D点距水平面的高度h=0.8 m.图6 小物块离开D点后恰好垂直碰击放在水平面上E点的固定倾斜挡板,已知小物块与传送带间的动摩擦因数μ=0.3,传送带以5 m/s恒定速率顺时针转动,g=10 m/s2.求:
(1)传送带AB两端的距离;
(2)小物块经过D点时对轨道的压力的大小;
(3)倾斜挡板与水平面间的夹角θ的正切值.走向考场
1.运动的合成和分解就是几个速度的数字相加减. ( )
2.以水平初速度抛出的物体,只受重力作用下的运动,叫平抛运动,它是匀变速曲线运动. ( )7.做圆周运动的物体所受的合力一定指向圆心,叫做向心力. ( )
8.做圆周运动的物体,当向心力突然消失或向心力不足时,物体做远离圆心的运动,这种现象叫做离心现象. ( )
9.物体做曲线运动的条件:如果物体所受合外力的方向跟物体的速度方向不在一条直线上时,物体就做曲线运动. ( )答案 1.×(订正:进行运动合成和分解时,速度、加速度、位移都是矢量,遵守平行四边形定则) 2.√ 3.√
4.√ 5.√ 6.√ 7.×(订正:做匀速圆周运动的物体,所受的合外力一定指向圆心,产生向心加速度,这种力叫向心力) 8.√ 9.√ 10.√1.物体做曲线运动的条件和特点各是什么?物体做曲线运动时速度的方向、加速度(合外力)的方向、运动轨迹三者是怎样的关系?
提示:(1)物体做曲线运动的条件
物体所受合外力(或加速度)的方向与物体的速度方向不在同一条直线上.
(2)物体做曲线运动的特点
①运动质点在某一点的瞬时速度方向,就是通过这一点的曲线的切线方向.②曲线运动是变速运动,这是因为曲线运动的速度方向是不断变化的.
③做曲线运动的质点,其所受的合外力一定不为零,一定具有加速度.
(3)速度的方向、加速度(合外力)的方向、运动轨迹三者的关系是:质点的运动轨迹夹在速度方向与加速度(合外力)方向之间,且速度方向沿轨迹这一点切线方向、加速度(合外力)方向指向轨迹的凹侧.
易错:不能准确判断曲线运动速度方向、加速度(合外力)方向、轨迹三者之间的关系.2.研究曲线运动的基本方法是——运动的合成与分解,它应用了运动的哪些性质?
提示:运动的合成与分解应用了合运动与分运动的以下性质
①等时性
合运动和分运动经历的时间相等,即同时开始,同时进行,同时停止.
②独立性
一个物体同时参与几个分运动,各分运动独立进行,不受其他运动的影响.③等效性
各分运动的规律叠加起来与合运动的规律有完全相同的效果.
④运动的矢量性:加速度、速度、位移都是矢量,其合成与分解遵循平行四边形定则.
易混:混淆运动的分解与力的分解方法.3.对于匀变速曲线运动问题处理的基本思路是“化曲为直”,具体应如何分解?平抛运动问题处理的基本方法也是分解速度和位移,如何求解平抛运动的合速度及合位移?
提示:(1)匀变速曲线运动的分解方法是沿恒力方向和垂直恒力方向分解,沿垂直恒力方向上做匀速直线运动,沿恒力方向上做匀加速直线运动,这种观点是研究匀变速曲线运动的理论基础,这种观点是力的独立作用原理的体现.易混:混淆θ与α的关系,认为θ=α或θ=2α.4.物体做圆周运动的原因是什么?向心力与物体所受的合力是一回事吗?
提示:力是改变物体运动状态的原因.物体之所以做圆周运动,是因为它受到向心力的作用.向心力是沿与速度垂直方向上所有力的合力,但不一定是物体所受合力,仅当物体做匀速圆周运动时,物体所受向心力由合力提供.
在匀速圆周运动中,由于物体运动的速率不变,动能不变,故物体所受合力与速度时刻垂直、不做功,其方向指向圆心,产生向心加速度,只改变速度的方向.在变速圆周运动中,由于物体运动的速率在改变,动能在改变,故物体受到的合力不指向圆心,即与速度不垂直,合力要做功.合力沿半径方向的分力充当向心力,产生向心加速度,改变速度的方向;合力沿切线方向的分力产生切向加速度,改变速度的大小.
误区:误认为向心力是性质力,受力分析时认为向心力是物体实际受到的力.
易错:变速圆周运动中把物体所受的合力当作向心力.5.圆周运动的动力学问题的解题思路是什么?
易错:不能利用几何关系确定轨道半径.6.物体做匀速圆周运动的条件有哪些?什么条件下物体做向心运动?什么条件下物体做离心运动?
陷阱:物体做离心运动要受到离心力的作用.7.如图1所示,没有物体支撑的小球,例如绳子拴小球、小球在环形轨道的内侧,在竖直平面内做圆周运动.试分析小球能通过最高点的临界条件.图1 易错:找不准小球能通过最高点的临界条件,v>0,就认为小球能在竖直平面内做完整的圆周运动.8.如图2所示,有物体支撑的小球在竖直平面内做圆周运动过最高点的情况:(例如,硬杆、弯管、汽车过拱桥等)
试分析小球能做完整圆周运动的临界条件是什么?并分析在最高点杆对球的作用力的方向.图2 ①当小球通过最高点的速度v=v0时,小球的重力刚好提供做圆周运动的向心力;
②当小球通过最高点的速度v
易失分:不能正确使用假设法分析求解小球在最高点的受力情况. 猜想一 对运动的合成与分解的考查
命题依据:该考点虽然近几年不是高考的高频考点,但它却是一个较重要的考点,可从不同角度、背景考查考生对曲线运动的处理能力,下面设计的考题是小船渡河问题,是典型的运动合成与分解问题.从过河的最短位移这个角度进行考查,是明年高考重要的考点.试题设计
1.一条船要在最短时间内渡过宽为100 m的河,已知河水的速度v1与船离河岸的距离x的关系如图3甲所示,船在静水中的速度v2与时间t的关系如图乙所示.图3 则以下判断中正确的是 ( ).
A.船渡河的最短时间为25 s
B.船运动的轨迹可能是直线
C.船在河水中航行的加速度大小为a=0.4 m/s2
D.船在河水中的最大速度是5 m/s答案 C猜想二 对平抛运动的考查
命题依据:分析近三年的高考试题,对平抛运动的理解与应用是高考必考内容,为高考的高频考点,主要考查平抛运动规律的应用.下面设计的考题是已知平抛运动某时刻运动的方向,来求解其他物理量,具有预测性.试题设计
2.如图4所示,从某高度水平抛出一小球,经过时间t到达地面时,速度与水平方向的夹角为θ,不计空气阻力,重力加速度为g.下列说法正确的是 ( ).图4 答案 D猜想三 对圆周运动动力学的考查
命题依据:近几年高考中对圆周运动单独考查的试题不多,但圆周运动是高中物理中三种典型运动之一,预测明年可从一个新的角度进行考查.下面设计的考题总以小球在光滑水平面上做半径突变的圆周运动为背景分析细线的拉力F随时间t的变化图象,具有一定的创新性和预测性.试题设计
3.如图5所示,在光滑的水平面上固定两个直立的小铁钉,相距l,长为3l不可伸长的轻质细线一端固定在右侧铁钉上,另一端拴着一个小钢珠,将细线拉直,使小钢珠与两铁钉位于同一直线上.小钢珠以一定的初速度垂直于纸面从图示位置开始运动并开始计时,在小钢珠与铁钉碰撞前,细线拉力F随时间t的变化图象应是 ( ).图5 答案 B 猜想四 对圆周运动与抛体运动相结合的考查
命题依据:近几年高考中对圆周运动与抛体运动、天体运动、动能定理、机械能守恒定律、功能关系相结合的考查较为频繁.预计2014年会重点考查.例:水平面内的圆周运动与平抛运动相结合,竖直平面内的圆周运动与平抛运动相结合等.下面设计的考题为新情景的直线运动,竖直平面内的圆周运动与平抛运动相结合的问题,该题综合性强,为一较好的预测题.试题设计
4.如图6所示,一质量为m=1 kg的小物块轻轻放在水平匀速运动的传送带上的A点,随传送带运动到B点,小物块从C点沿圆弧切线进入竖直光滑的半圆轨道恰能做圆周运动,已知圆弧半径R=0.9 m,轨道最低点为D,D点距水平面的高度h=0.8 m.图6 小物块离开D点后恰好垂直碰击放在水平面上E点的固定倾斜挡板,已知小物块与传送带间的动摩擦因数μ=0.3,传送带以5 m/s恒定速率顺时针转动,g=10 m/s2.求:
(1)传送带AB两端的距离;
(2)小物块经过D点时对轨道的压力的大小;
(3)倾斜挡板与水平面间的夹角θ的正切值.走向考场
同课章节目录
