安徽省合肥市第六十八中学2022-2023学年上学期九年级数学上册第三次月考测试题 (含解析)
文档属性
| 名称 | 安徽省合肥市第六十八中学2022-2023学年上学期九年级数学上册第三次月考测试题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 321.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-29 23:10:00 | ||
图片预览

文档简介
安徽省合肥市第六十八中学
2022-2023学年第一学期九年级数学第三次月考测试题(附答案)
一、选择题(满分40分)
1.下列是有理数的是( )
A.tan45° B.sin45° C.cos45° D.sin60°
2.若,则的值为( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠B的正切值为( )
A.3 B. C. D.
4.函数y=中,自变量x的取值范围是( )
A.x>0 B.x<0
C.x≠0的一切实数 D.x取任意实数
5.如图所示,有一山坡在水平方向每前进100m就升高60m,那么山坡的坡度i为( )
A.3:5 B.2:3 C.4:7 D.5:3
6.如图,直线y=与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
A. B. C. D.
7.已知二次函数y=x2+x+c的图象与x轴的一个交点为(2,0),则它与x轴的另一个交点坐标是( )
A.(1,0) B.(﹣1,0) C.(2,0) D.(﹣3,0)
8.关于抛物线y=﹣x2+2x,下列说法错误的是( )
A.该抛物线经过原点 B.该抛物线的对称轴是直线x=1
C.该抛物线的最大值为1 D.当x>0时,y随x增大而减小
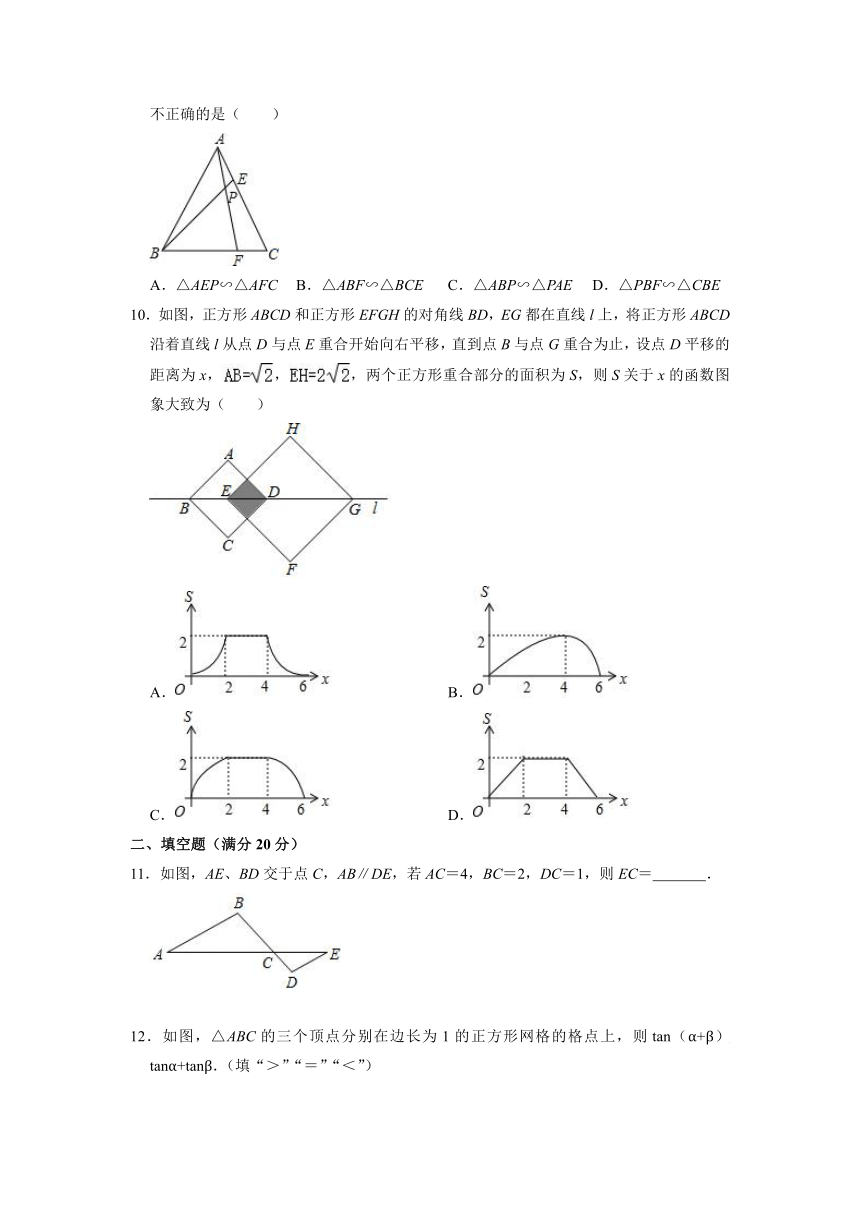
9.如图,在等边三角形ABC中,点E,F分别在AC,BC上,且AE AC=AP AF,则下列不正确的是( )
A.△AEP∽△AFC B.△ABF∽△BCE C.△ABP∽△PAE D.△PBF∽△CBE
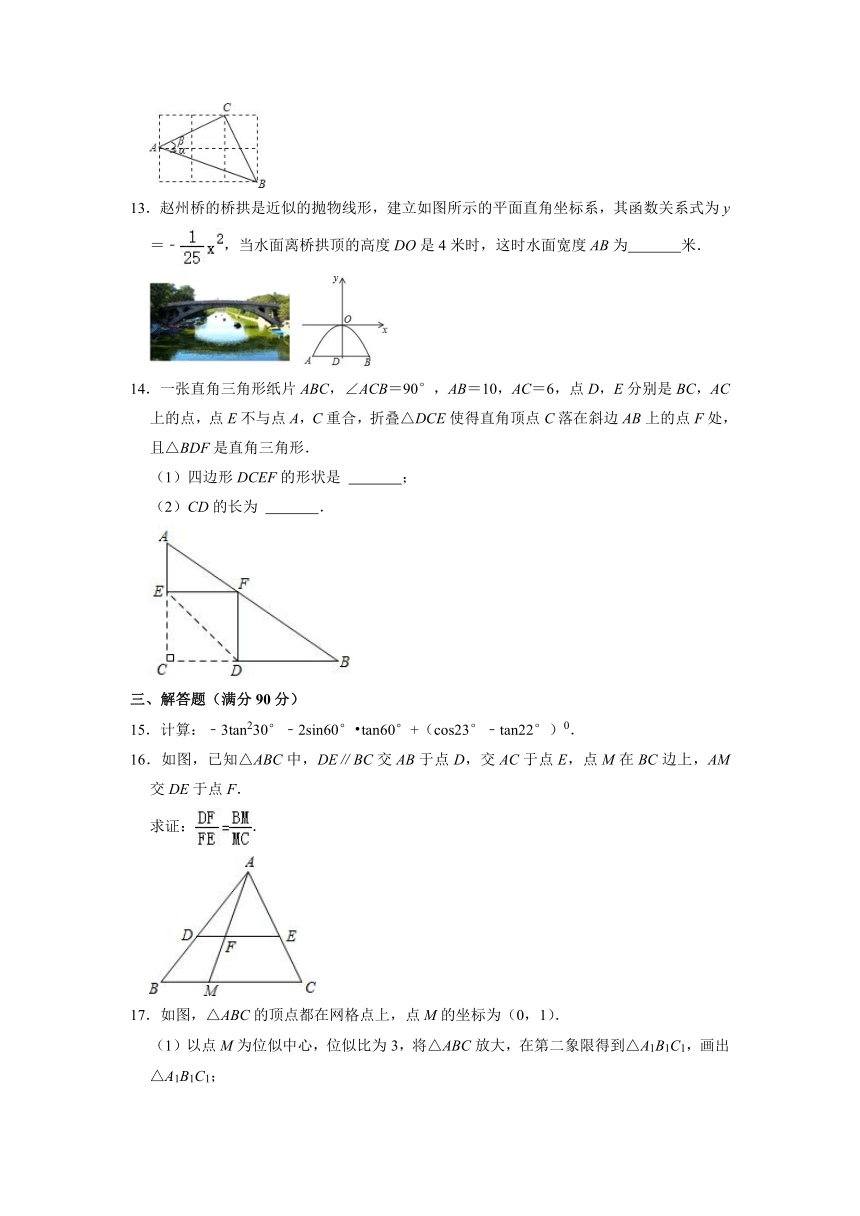
10.如图,正方形ABCD和正方形EFGH的对角线BD,EG都在直线l上,将正方形ABCD沿着直线l从点D与点E重合开始向右平移,直到点B与点G重合为止,设点D平移的距离为x,,,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
A. B.
C. D.
二、填空题(满分20分)
11.如图,AE、BD交于点C,AB∥DE,若AC=4,BC=2,DC=1,则EC= .
12.如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β) tanα+tanβ.(填“>”“=”“<”)
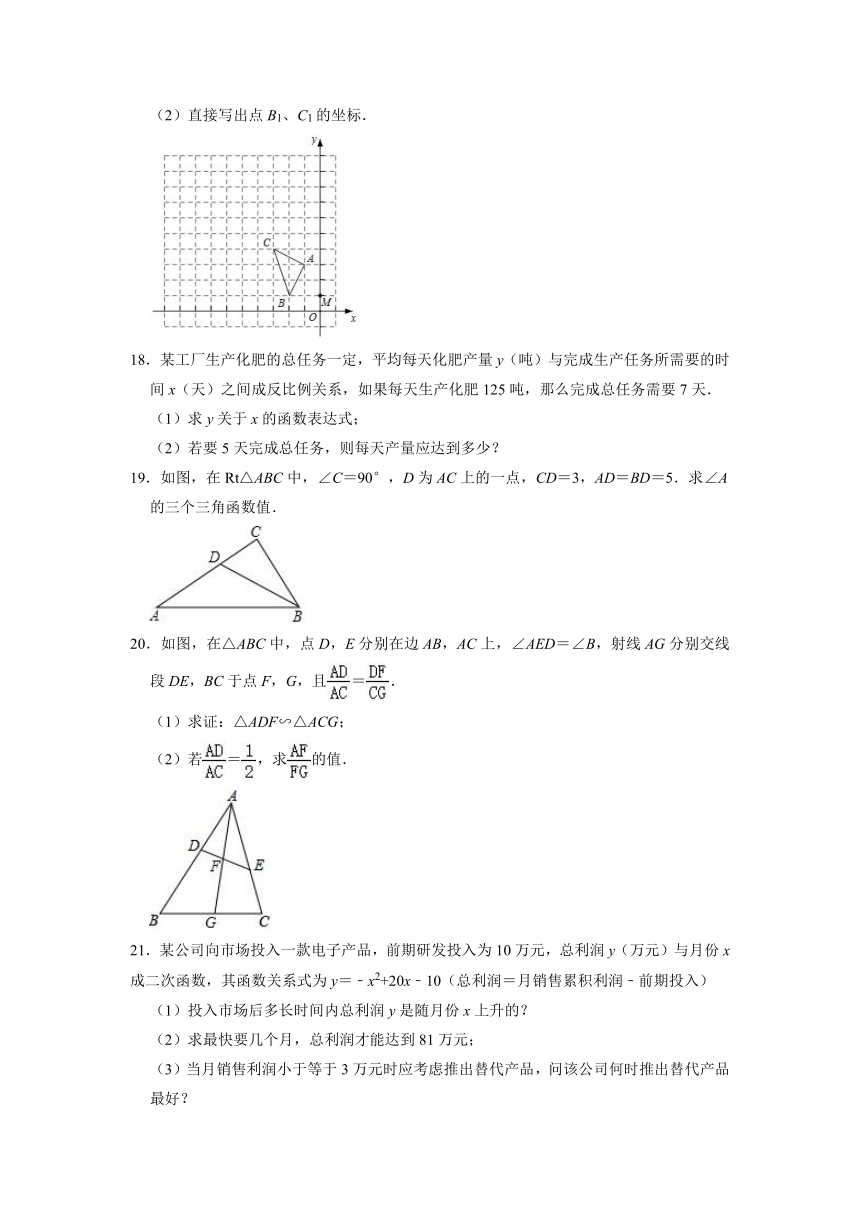
13.赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数关系式为y=﹣,当水面离桥拱顶的高度DO是4米时,这时水面宽度AB为 米.
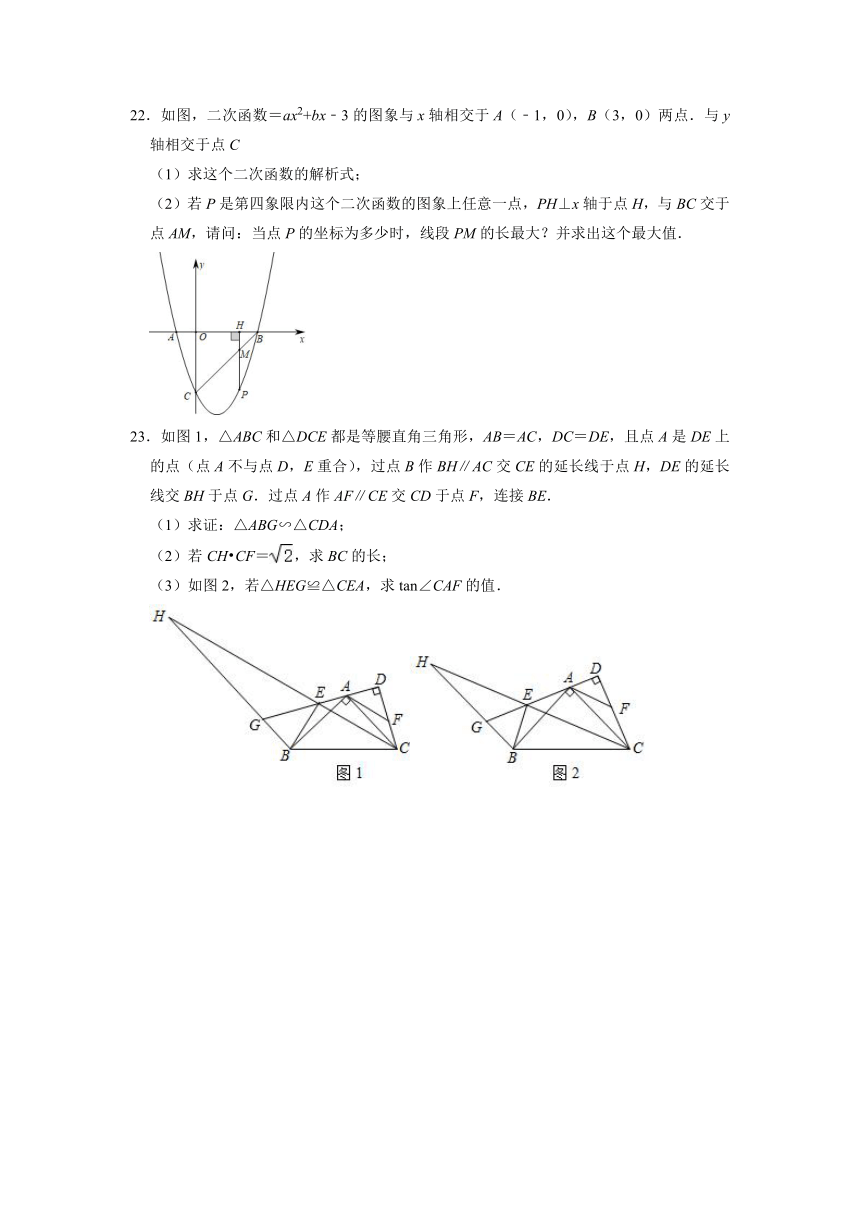
14.一张直角三角形纸片ABC,∠ACB=90°,AB=10,AC=6,点D,E分别是BC,AC上的点,点E不与点A,C重合,折叠△DCE使得直角顶点C落在斜边AB上的点F处,且△BDF是直角三角形.
(1)四边形DCEF的形状是 ;
(2)CD的长为 .
三、解答题(满分90分)
15.计算:﹣3tan230°﹣2sin60° tan60°+(cos23°﹣tan22°)0.
16.如图,已知△ABC中,DE∥BC交AB于点D,交AC于点E,点M在BC边上,AM交DE于点F.
求证:.
17.如图,△ABC的顶点都在网格点上,点M的坐标为(0,1).
(1)以点M为位似中心,位似比为3,将△ABC放大,在第二象限得到△A1B1C1,画出△A1B1C1;
(2)直接写出点B1、C1的坐标.
18.某工厂生产化肥的总任务一定,平均每天化肥产量y(吨)与完成生产任务所需要的时间x(天)之间成反比例关系,如果每天生产化肥125吨,那么完成总任务需要7天.
(1)求y关于x的函数表达式;
(2)若要5天完成总任务,则每天产量应达到多少?
19.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
20.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
21.某公司向市场投入一款电子产品,前期研发投入为10万元,总利润y(万元)与月份x成二次函数,其函数关系式为y=﹣x2+20x﹣10(总利润=月销售累积利润﹣前期投入)
(1)投入市场后多长时间内总利润y是随月份x上升的?
(2)求最快要几个月,总利润才能达到81万元;
(3)当月销售利润小于等于3万元时应考虑推出替代产品,问该公司何时推出替代产品最好?
22.如图,二次函数=ax2+bx﹣3的图象与x轴相交于A(﹣1,0),B(3,0)两点.与y轴相交于点C
(1)求这个二次函数的解析式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点AM,请问:当点P的坐标为多少时,线段PM的长最大?并求出这个最大值.
23.如图1,△ABC和△DCE都是等腰直角三角形,AB=AC,DC=DE,且点A是DE上的点(点A不与点D,E重合),过点B作BH∥AC交CE的延长线于点H,DE的延长线交BH于点G.过点A作AF∥CE交CD于点F,连接BE.
(1)求证:△ABG∽△CDA;
(2)若CH CF=,求BC的长;
(3)如图2,若△HEG≌△CEA,求tan∠CAF的值.
参考答案
一、选择题(满分40分)
1.解:A、tan45°=1,是有理数,符合题意;
B、sin45°=,不是有理数,不符合题意;
C、cos45°=,不是有理数,不符合题意;
D、sin60°=,不是有理数,不符合题意;
故选:A.
2.解:∵=,
∴a=b,
即==.
故选:A.
3.解:在Rt△ABC中,∠C=90°,AC=1,BC=3,
则tanB==,
故选:B.
4.解:函数y=中,自变量x的取值范围是x≠0,
故选:C.
5.解:∵铅直高度为60m,水平宽度为100m,
∴山坡的坡度i=60:100=3:5,
故选:A.
6.解:当x=0时,y=3,
当y=0时,x=﹣4,
∴直线y=与x、y轴的交点A的坐标(﹣4,0)、B(0,3),
∴OA=4,OB=3,
由勾股定理得,AB=5,
则cos∠BAO==,
故选:A.
7.解:∵a=1,b=1,
∴,
即:2+x=﹣1,解得:x=﹣3,
∴二次函数与x轴的另一个交点为(﹣3,0),
也可求将点(2,0)代入解析式可求c=6,令y=0,可求解.
故选:D.
8.解:当抛物线y=﹣x2+2x,当x=0时,y=0,
∴经过原点,A正确,
配方得:y=﹣(x﹣1)2+1,
∴顶点坐标是(1,1),对称轴是直线x=1,根据a=﹣1<0,得出开口向下有最大值,当x>1时,y随x的增大而减小,
∴B、C说法正确;
D说法错误.
故选:D.
9.解:∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠C=∠BAC=60°,
∵AE AC=AP AF,
∴=,
∵∠PAE=∠CAF,
∴△PAE∽△CAF,
∴∠APE=∠C=60°,
∵∠APE=∠ABP+∠BAP=60°,∠BAP+∠CAF=60°,
∴∠CAF=∠ABE,
∴∠BAF=∠CBE,
∵∠ABF=∠C,
∴△ABF∽△BCE,
∵∠BPF=∠APE=∠C,∠PBF=∠CBE,
∴△PBF∽△CBE,
故选项A,B,D正确,
故选:C.
10.解:如图(1),当0≤x≤2时,;
如图(2),当2<x<4时,正方形ABCD在正方形EFGH内部,
则;
如图(3),当4≤x≤6时,BG=2﹣(x﹣4)=6﹣x,
∴.综上所述,选项A符合题意.
故选:A.
二、填空题(满分20分)
11.解:∵AB∥DE,
∴△ABC∽△ECD,
∴,
∵AC=4,BC=2,DC=1,
∴,
解得:CE=2.
故答案为:2
12.解:由正方形网格图可知,tanα=,tanβ=,
则tanα+tanβ=+=,
∵AC=BC,∠ACB=90°,
∴α+β=45°,
∴tan(α+β)=1,
∴tan(α+β)>tanα+tanβ,
故答案为:>.
13.解:当y=﹣4时,
﹣4=﹣,
解得,x1=﹣10,x2=10,
∴当水面离桥拱顶的高度DO是4米时,这时水面宽度AB为:10﹣(﹣10)=20(米),
故答案为:20.
14.解(1)∵△BDF是直角三角形.
∴FD⊥BC,
∴∠CDF=∠BDF=90°,
又∵∠ACB=90°,
∴∠CDF=∠BDF=∠ACB=90°,
∴四边形DCEF是矩形,
由折叠的性质可得:CD=DF,
∴四边形DCEF是正方形,
故答案为:正方形;
(2)在Rt△ACB中,由勾股定理得:
BC===8,
设CD=x,则DF=x,BD=8﹣x,
∵∠B=∠B,∠BDF=∠BCA=90°,
∴△BDF∽△BCA,
∴,
即,
解得:x=,
∴CD=.
三、解答题(满分90分)
15.解:原式=﹣3×()2﹣2××+1
=﹣3×﹣3+1
=﹣1﹣3+1
=﹣3.
16.证明:∵DE∥BC,
∴=,=
∴=,
∴=.
17.解:(1)如图,△A1B1C1即为所求.
(2)如图,B1(﹣6,1),C1(﹣9,10).
18.解:(1)设y=,
根据题意得:k=xy=125×7=875,
∴y关于x的函数表达式为y=;
(2)当x=5时,y==175(吨),
即若要5天完成总任务,则每天产量应达到175吨.
19.解:在Rt△BCD中,∵CD=3、BD=5,
∴BC===4,
又AC=AD+CD=8,
∴AB===4,
则sinA===,
cosA===,
tanA===.
20.(1)证明:∵∠AED=∠B,∠DAE=∠CAB,
∴∠ADF=∠C.
又∵=,
∴△ADF∽△ACG.
(2)∵△ADF∽△ACG,
∴=.
∵=,
∴=,
∴==1.
21.解:(1)∵y=﹣x2+20x﹣10=﹣(x﹣10)2+90,
∴当x<10时,y随x的增大而增大,
故投入市场后10个月内总利润y是随月份x上升的.
(2)当y=81时,可得:﹣(x﹣10)2+90=81,
解得:x1=7,x2=13,
故最快要7个月,总利润才能达到81万元.
(3)根据题意,得:﹣x2+20x﹣10﹣[﹣(x﹣1)2+20(x﹣1)﹣10]≤3,
整理,得:﹣2x+21≤3,
解得:x≥9,
答:该公司第9个月时推出替代产品最好.
22.解:(1)由题意得:,解得,
∴这个二次函数的解析式为y=x2﹣2x﹣3,
(2)当x=0时,y=3,则C为(0,﹣3),
易得直线BC的函数解析式为:y=x﹣3,
设P的坐标为(t,t2﹣2t﹣3)(0<t<3),则M的坐标为(t,t﹣3),
∴PM=t﹣3﹣(t2﹣2t﹣3)=﹣t2+3t
=﹣(t﹣)2+,
∵﹣1<0且0<t<3,
∴当t=时,PM取得最大值,最大值为,此时P的坐标为(,﹣).
23.证明:(1)∵BH∥AC,
∴∠ABG=∠BAC=90°,
∴∠BAG+∠AGB=90°,
∠BAG+∠CAD=90°,
∴∠AGB=∠CAD,
∵∠ABG=D=90°,
∴△ABG∽△CDA;
(2)∵BH∥AC,CH∥AF,
∴∠H=∠ACE,∠ACE=∠FAC,∠AFD=∠DCE=45°,
∴∠H=∠FAC,
∵∠CBH=∠ABC+∠ABG=45°+90°=135°,
∠AFC=180°﹣∠AFD=135°,
∴∠CBH=∠AFC,
∴△HBC∽△AFC,
∴=,
∴AC BC=CH CF=,
∵BC=AC,
∴BC=;
(3)如图2,
作BP⊥DG于P,
∴∠APB=90°,
∴∠PAB+∠ABP=90°,
∵∠BAC=90°,
∴∠PAB+∠CAD=90°,
∴∠CAD=∠ABP,
∵AB=AC,
∠D=∠APB=90°,
∴△ABP≌△CAD(AAS),
∴BP=AD,AP=DC,
∵DE=DC,
∴AP=DE,
∴AP﹣AE=DE﹣AE,
∴PE=AD,
∴BP=PE,
∴△PBE是等腰直角三角形,
∴∠BEP=45°,
∵∠DEC=45°,
∴∠BEC=180°﹣∠PEB﹣∠DEC=90°,
∵∠AOC=∠BOE,
∴∠ABE=∠ACE=∠CAF,
∵△HEG≌△CEA,
∴GE=AE,
∴BE=AE=,
∴∠PAB=∠ABE,
∴∠PAB=∠CAF,
设PB=PE=k,
∴AE=BE=k,
∴AP=PE+AE=(k,
∴tan∠CAF=tan∠PAB=
=
=﹣1.
2022-2023学年第一学期九年级数学第三次月考测试题(附答案)
一、选择题(满分40分)
1.下列是有理数的是( )
A.tan45° B.sin45° C.cos45° D.sin60°
2.若,则的值为( )
A. B. C. D.
3.在Rt△ABC中,∠C=90°,AC=1,BC=3,则∠B的正切值为( )
A.3 B. C. D.
4.函数y=中,自变量x的取值范围是( )
A.x>0 B.x<0
C.x≠0的一切实数 D.x取任意实数
5.如图所示,有一山坡在水平方向每前进100m就升高60m,那么山坡的坡度i为( )
A.3:5 B.2:3 C.4:7 D.5:3
6.如图,直线y=与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
A. B. C. D.
7.已知二次函数y=x2+x+c的图象与x轴的一个交点为(2,0),则它与x轴的另一个交点坐标是( )
A.(1,0) B.(﹣1,0) C.(2,0) D.(﹣3,0)
8.关于抛物线y=﹣x2+2x,下列说法错误的是( )
A.该抛物线经过原点 B.该抛物线的对称轴是直线x=1
C.该抛物线的最大值为1 D.当x>0时,y随x增大而减小
9.如图,在等边三角形ABC中,点E,F分别在AC,BC上,且AE AC=AP AF,则下列不正确的是( )
A.△AEP∽△AFC B.△ABF∽△BCE C.△ABP∽△PAE D.△PBF∽△CBE
10.如图,正方形ABCD和正方形EFGH的对角线BD,EG都在直线l上,将正方形ABCD沿着直线l从点D与点E重合开始向右平移,直到点B与点G重合为止,设点D平移的距离为x,,,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
A. B.
C. D.
二、填空题(满分20分)
11.如图,AE、BD交于点C,AB∥DE,若AC=4,BC=2,DC=1,则EC= .
12.如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β) tanα+tanβ.(填“>”“=”“<”)
13.赵州桥的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数关系式为y=﹣,当水面离桥拱顶的高度DO是4米时,这时水面宽度AB为 米.
14.一张直角三角形纸片ABC,∠ACB=90°,AB=10,AC=6,点D,E分别是BC,AC上的点,点E不与点A,C重合,折叠△DCE使得直角顶点C落在斜边AB上的点F处,且△BDF是直角三角形.
(1)四边形DCEF的形状是 ;
(2)CD的长为 .
三、解答题(满分90分)
15.计算:﹣3tan230°﹣2sin60° tan60°+(cos23°﹣tan22°)0.
16.如图,已知△ABC中,DE∥BC交AB于点D,交AC于点E,点M在BC边上,AM交DE于点F.
求证:.
17.如图,△ABC的顶点都在网格点上,点M的坐标为(0,1).
(1)以点M为位似中心,位似比为3,将△ABC放大,在第二象限得到△A1B1C1,画出△A1B1C1;
(2)直接写出点B1、C1的坐标.
18.某工厂生产化肥的总任务一定,平均每天化肥产量y(吨)与完成生产任务所需要的时间x(天)之间成反比例关系,如果每天生产化肥125吨,那么完成总任务需要7天.
(1)求y关于x的函数表达式;
(2)若要5天完成总任务,则每天产量应达到多少?
19.如图,在Rt△ABC中,∠C=90°,D为AC上的一点,CD=3,AD=BD=5.求∠A的三个三角函数值.
20.如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且=.
(1)求证:△ADF∽△ACG;
(2)若=,求的值.
21.某公司向市场投入一款电子产品,前期研发投入为10万元,总利润y(万元)与月份x成二次函数,其函数关系式为y=﹣x2+20x﹣10(总利润=月销售累积利润﹣前期投入)
(1)投入市场后多长时间内总利润y是随月份x上升的?
(2)求最快要几个月,总利润才能达到81万元;
(3)当月销售利润小于等于3万元时应考虑推出替代产品,问该公司何时推出替代产品最好?
22.如图,二次函数=ax2+bx﹣3的图象与x轴相交于A(﹣1,0),B(3,0)两点.与y轴相交于点C
(1)求这个二次函数的解析式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点AM,请问:当点P的坐标为多少时,线段PM的长最大?并求出这个最大值.
23.如图1,△ABC和△DCE都是等腰直角三角形,AB=AC,DC=DE,且点A是DE上的点(点A不与点D,E重合),过点B作BH∥AC交CE的延长线于点H,DE的延长线交BH于点G.过点A作AF∥CE交CD于点F,连接BE.
(1)求证:△ABG∽△CDA;
(2)若CH CF=,求BC的长;
(3)如图2,若△HEG≌△CEA,求tan∠CAF的值.
参考答案
一、选择题(满分40分)
1.解:A、tan45°=1,是有理数,符合题意;
B、sin45°=,不是有理数,不符合题意;
C、cos45°=,不是有理数,不符合题意;
D、sin60°=,不是有理数,不符合题意;
故选:A.
2.解:∵=,
∴a=b,
即==.
故选:A.
3.解:在Rt△ABC中,∠C=90°,AC=1,BC=3,
则tanB==,
故选:B.
4.解:函数y=中,自变量x的取值范围是x≠0,
故选:C.
5.解:∵铅直高度为60m,水平宽度为100m,
∴山坡的坡度i=60:100=3:5,
故选:A.
6.解:当x=0时,y=3,
当y=0时,x=﹣4,
∴直线y=与x、y轴的交点A的坐标(﹣4,0)、B(0,3),
∴OA=4,OB=3,
由勾股定理得,AB=5,
则cos∠BAO==,
故选:A.
7.解:∵a=1,b=1,
∴,
即:2+x=﹣1,解得:x=﹣3,
∴二次函数与x轴的另一个交点为(﹣3,0),
也可求将点(2,0)代入解析式可求c=6,令y=0,可求解.
故选:D.
8.解:当抛物线y=﹣x2+2x,当x=0时,y=0,
∴经过原点,A正确,
配方得:y=﹣(x﹣1)2+1,
∴顶点坐标是(1,1),对称轴是直线x=1,根据a=﹣1<0,得出开口向下有最大值,当x>1时,y随x的增大而减小,
∴B、C说法正确;
D说法错误.
故选:D.
9.解:∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠C=∠BAC=60°,
∵AE AC=AP AF,
∴=,
∵∠PAE=∠CAF,
∴△PAE∽△CAF,
∴∠APE=∠C=60°,
∵∠APE=∠ABP+∠BAP=60°,∠BAP+∠CAF=60°,
∴∠CAF=∠ABE,
∴∠BAF=∠CBE,
∵∠ABF=∠C,
∴△ABF∽△BCE,
∵∠BPF=∠APE=∠C,∠PBF=∠CBE,
∴△PBF∽△CBE,
故选项A,B,D正确,
故选:C.
10.解:如图(1),当0≤x≤2时,;
如图(2),当2<x<4时,正方形ABCD在正方形EFGH内部,
则;
如图(3),当4≤x≤6时,BG=2﹣(x﹣4)=6﹣x,
∴.综上所述,选项A符合题意.
故选:A.
二、填空题(满分20分)
11.解:∵AB∥DE,
∴△ABC∽△ECD,
∴,
∵AC=4,BC=2,DC=1,
∴,
解得:CE=2.
故答案为:2
12.解:由正方形网格图可知,tanα=,tanβ=,
则tanα+tanβ=+=,
∵AC=BC,∠ACB=90°,
∴α+β=45°,
∴tan(α+β)=1,
∴tan(α+β)>tanα+tanβ,
故答案为:>.
13.解:当y=﹣4时,
﹣4=﹣,
解得,x1=﹣10,x2=10,
∴当水面离桥拱顶的高度DO是4米时,这时水面宽度AB为:10﹣(﹣10)=20(米),
故答案为:20.
14.解(1)∵△BDF是直角三角形.
∴FD⊥BC,
∴∠CDF=∠BDF=90°,
又∵∠ACB=90°,
∴∠CDF=∠BDF=∠ACB=90°,
∴四边形DCEF是矩形,
由折叠的性质可得:CD=DF,
∴四边形DCEF是正方形,
故答案为:正方形;
(2)在Rt△ACB中,由勾股定理得:
BC===8,
设CD=x,则DF=x,BD=8﹣x,
∵∠B=∠B,∠BDF=∠BCA=90°,
∴△BDF∽△BCA,
∴,
即,
解得:x=,
∴CD=.
三、解答题(满分90分)
15.解:原式=﹣3×()2﹣2××+1
=﹣3×﹣3+1
=﹣1﹣3+1
=﹣3.
16.证明:∵DE∥BC,
∴=,=
∴=,
∴=.
17.解:(1)如图,△A1B1C1即为所求.
(2)如图,B1(﹣6,1),C1(﹣9,10).
18.解:(1)设y=,
根据题意得:k=xy=125×7=875,
∴y关于x的函数表达式为y=;
(2)当x=5时,y==175(吨),
即若要5天完成总任务,则每天产量应达到175吨.
19.解:在Rt△BCD中,∵CD=3、BD=5,
∴BC===4,
又AC=AD+CD=8,
∴AB===4,
则sinA===,
cosA===,
tanA===.
20.(1)证明:∵∠AED=∠B,∠DAE=∠CAB,
∴∠ADF=∠C.
又∵=,
∴△ADF∽△ACG.
(2)∵△ADF∽△ACG,
∴=.
∵=,
∴=,
∴==1.
21.解:(1)∵y=﹣x2+20x﹣10=﹣(x﹣10)2+90,
∴当x<10时,y随x的增大而增大,
故投入市场后10个月内总利润y是随月份x上升的.
(2)当y=81时,可得:﹣(x﹣10)2+90=81,
解得:x1=7,x2=13,
故最快要7个月,总利润才能达到81万元.
(3)根据题意,得:﹣x2+20x﹣10﹣[﹣(x﹣1)2+20(x﹣1)﹣10]≤3,
整理,得:﹣2x+21≤3,
解得:x≥9,
答:该公司第9个月时推出替代产品最好.
22.解:(1)由题意得:,解得,
∴这个二次函数的解析式为y=x2﹣2x﹣3,
(2)当x=0时,y=3,则C为(0,﹣3),
易得直线BC的函数解析式为:y=x﹣3,
设P的坐标为(t,t2﹣2t﹣3)(0<t<3),则M的坐标为(t,t﹣3),
∴PM=t﹣3﹣(t2﹣2t﹣3)=﹣t2+3t
=﹣(t﹣)2+,
∵﹣1<0且0<t<3,
∴当t=时,PM取得最大值,最大值为,此时P的坐标为(,﹣).
23.证明:(1)∵BH∥AC,
∴∠ABG=∠BAC=90°,
∴∠BAG+∠AGB=90°,
∠BAG+∠CAD=90°,
∴∠AGB=∠CAD,
∵∠ABG=D=90°,
∴△ABG∽△CDA;
(2)∵BH∥AC,CH∥AF,
∴∠H=∠ACE,∠ACE=∠FAC,∠AFD=∠DCE=45°,
∴∠H=∠FAC,
∵∠CBH=∠ABC+∠ABG=45°+90°=135°,
∠AFC=180°﹣∠AFD=135°,
∴∠CBH=∠AFC,
∴△HBC∽△AFC,
∴=,
∴AC BC=CH CF=,
∵BC=AC,
∴BC=;
(3)如图2,
作BP⊥DG于P,
∴∠APB=90°,
∴∠PAB+∠ABP=90°,
∵∠BAC=90°,
∴∠PAB+∠CAD=90°,
∴∠CAD=∠ABP,
∵AB=AC,
∠D=∠APB=90°,
∴△ABP≌△CAD(AAS),
∴BP=AD,AP=DC,
∵DE=DC,
∴AP=DE,
∴AP﹣AE=DE﹣AE,
∴PE=AD,
∴BP=PE,
∴△PBE是等腰直角三角形,
∴∠BEP=45°,
∵∠DEC=45°,
∴∠BEC=180°﹣∠PEB﹣∠DEC=90°,
∵∠AOC=∠BOE,
∴∠ABE=∠ACE=∠CAF,
∵△HEG≌△CEA,
∴GE=AE,
∴BE=AE=,
∴∠PAB=∠ABE,
∴∠PAB=∠CAF,
设PB=PE=k,
∴AE=BE=k,
∴AP=PE+AE=(k,
∴tan∠CAF=tan∠PAB=
=
=﹣1.
同课章节目录
