正弦定理
图片预览




文档简介
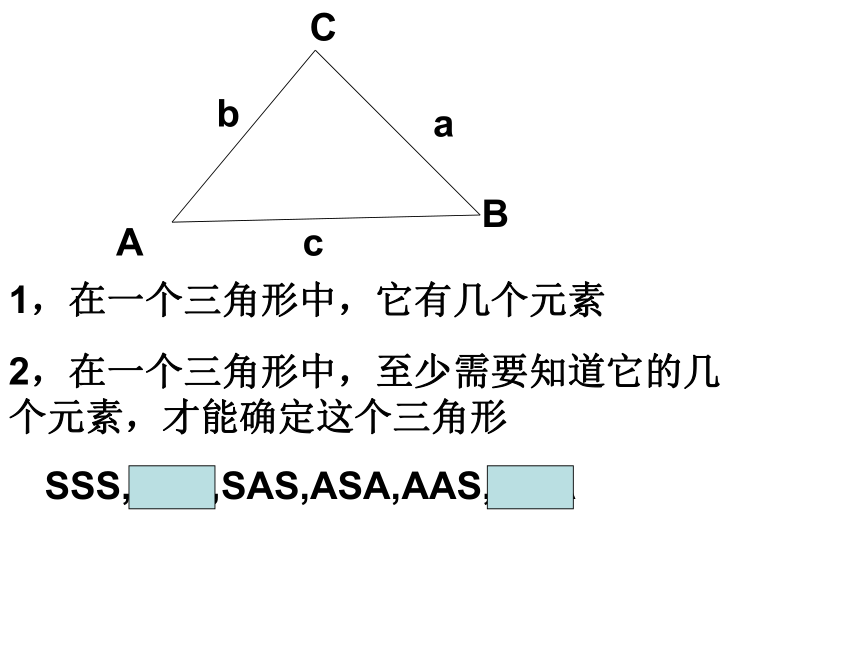
课件12张PPT。必修5:第一章,解三角形问题一:什么叫解三角形?1,你怎样测量出旗杆的高度?2,数学:不用直接测量,而知道一棵树的高度这就是数学!h=tanaxa1,在一个三角形中,它有几个元素2,在一个三角形中,至少需要知道它的几个元素,才能确定这个三角形ACBcabSSS,SSA,SAS,ASA,AAS,AAA问题一:什么叫解三角形? 一般的,三角形中的三个角A、B、C和它对应的三条边a、b、c叫做三角形的元素。
已知三角形的几( )个元素求其他元素的过程就叫解三角形31、1、1正弦定理问题二:三角形中的三个角A、B、C和它对应的三条边a、b、c之间有什么样的数量关系呢?
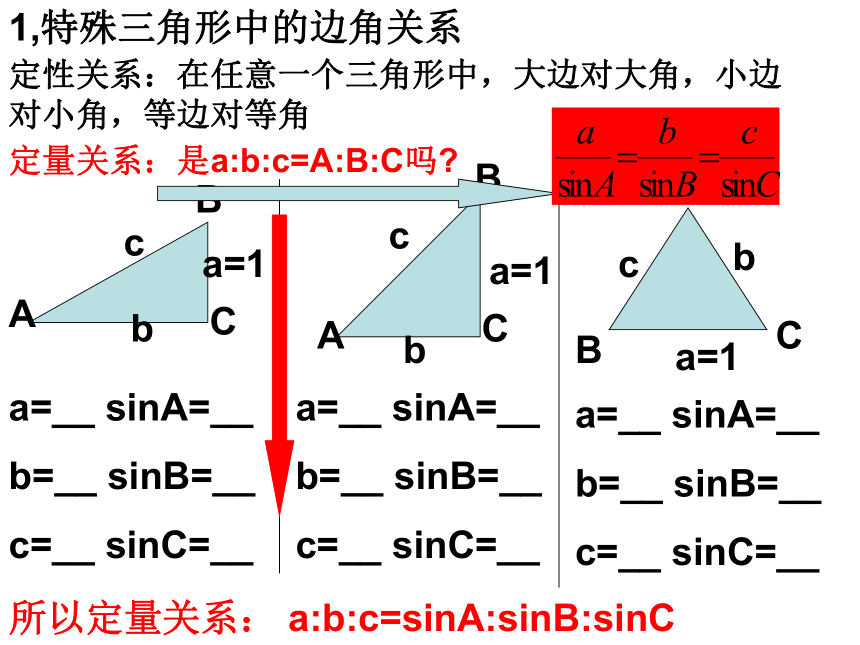
ABca=1bCABca=1bABca=1bCC定性关系:在任意一个三角形中,大边对大角,小边对小角,等边对等角定量关系:是a:b:c=A:B:C吗?a=__ sinA=__
b=__ sinB=__
c=__ sinC=__a=__ sinA=__
b=__ sinB=__
c=__ sinC=__a=__ sinA=__
b=__ sinB=__
c=__ sinC=__所以定量关系:a:b:c=sinA:sinB:sinC1,特殊三角形中的边角关系2,那么,对于一般三角形中,上述关系
a:b:c=sinA:sinB:sinC或者 是
否仍然成立呢?D问题二:三角形中的三个角A、B、C和它对应的三条边a、b、c之间有什么样的数量关系呢?
正弦定理1:在一个三角形中,各边之比等于各边对角的正弦值之比,即a:b:c=sinA:sinB:sinC正弦定理2:在一个三角形中,各边和它所对角的正弦
值之比相等,即问题三:通过观察例1,例2,什么情况下利用正弦定理解三角形? 在已知一组对应边角大小时,可利用正弦定理解三角形问题四:在确定的一个三角形中,=k(2R)在三角形ABC中,A=30度,a=1,求该三角形外接圆的半径。所以根据正弦定理可以进行边角互化边化角:角化边:a=sinAk,b=sinBk,c=sinCksinA=a/k, sinB=b/k, sinC=c/k边角互化的应用在三角形ABC中:1,若sin2C= sin2A+sin2B,则它为_______三角形2,若sinA>sinB,则A_____B(AB的大小关系)课内小结正弦定理:1,表达式:2,作用:体现边角之间的数量关系3,适用范围:已知一组对应边角的大小(AAS,ASA,SSA)4,应用:利用定理解三角形利用定理边角互化
已知三角形的几( )个元素求其他元素的过程就叫解三角形31、1、1正弦定理问题二:三角形中的三个角A、B、C和它对应的三条边a、b、c之间有什么样的数量关系呢?
ABca=1bCABca=1bABca=1bCC定性关系:在任意一个三角形中,大边对大角,小边对小角,等边对等角定量关系:是a:b:c=A:B:C吗?a=__ sinA=__
b=__ sinB=__
c=__ sinC=__a=__ sinA=__
b=__ sinB=__
c=__ sinC=__a=__ sinA=__
b=__ sinB=__
c=__ sinC=__所以定量关系:a:b:c=sinA:sinB:sinC1,特殊三角形中的边角关系2,那么,对于一般三角形中,上述关系
a:b:c=sinA:sinB:sinC或者 是
否仍然成立呢?D问题二:三角形中的三个角A、B、C和它对应的三条边a、b、c之间有什么样的数量关系呢?
正弦定理1:在一个三角形中,各边之比等于各边对角的正弦值之比,即a:b:c=sinA:sinB:sinC正弦定理2:在一个三角形中,各边和它所对角的正弦
值之比相等,即问题三:通过观察例1,例2,什么情况下利用正弦定理解三角形? 在已知一组对应边角大小时,可利用正弦定理解三角形问题四:在确定的一个三角形中,=k(2R)在三角形ABC中,A=30度,a=1,求该三角形外接圆的半径。所以根据正弦定理可以进行边角互化边化角:角化边:a=sinAk,b=sinBk,c=sinCksinA=a/k, sinB=b/k, sinC=c/k边角互化的应用在三角形ABC中:1,若sin2C= sin2A+sin2B,则它为_______三角形2,若sinA>sinB,则A_____B(AB的大小关系)课内小结正弦定理:1,表达式:2,作用:体现边角之间的数量关系3,适用范围:已知一组对应边角的大小(AAS,ASA,SSA)4,应用:利用定理解三角形利用定理边角互化
