期末考试仿真模拟试卷04-2022-2023学年高三数学下学期期初考试仿真模拟试卷(江苏专用)(含解析)
文档属性
| 名称 | 期末考试仿真模拟试卷04-2022-2023学年高三数学下学期期初考试仿真模拟试卷(江苏专用)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-30 14:53:20 | ||
图片预览




文档简介
2022-2023学年高三数学下学期期初考试仿真模拟试卷04
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则集合的子集个数为( )
A. 1 B. 2 C. 3 D. 4
2.复数满足,则( )
A. B. C. D. 5
3.一个圆锥的侧面展开图恰好是一个半径为1的半圆,则该圆锥的表面积为( )
A. B. C. D.
4.已知平面向量的夹角为,且,则( )
A. 4 B. 2 C. 1 D.
5.某小区共有3个核酸检测点同时进行检测,有6名志愿者被分配到这3个检测点参加服务,6人中有4名“熟手”和2名“生手”,1名“生手”至少需要1名“熟手”进行检测工作的传授,每个检测点至少需要1名“熟手”,且2名“生手”不能分配到同一个检测点,则不同的分配方案种数是( )
A. 72 B. 108 C. 216 D. 432
6.已知数列的前n项和组成的数列满足,,,则数列的通项公式为( )
A. B.
C. D.
7.设,分别为双曲线(,)的左、右焦点,A为双曲线的左顶点,以为直径的圆交双曲线的某条渐近线于M,N两点,且,(如图),则该双曲线的离心率为( )
A. B. C. D.
8.不等式在上恒成立,则实数的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知数据,,,…,的众数、平均数、方差、第80百分位数分别是,,,,数据,,,…,的众数、平均数、方差、第80百分位数分别是,,,,且满足,则下列结论正确的是( )
A. B.
C. D.
10.向量 函数,则下述结论正确的有( )
A. 若的图像关于直线对称,则可能为
B. 周期时,则的图像关于点对称
C. 若的图像向左平移个单位长度后得到一个偶函数,则的最小值为
D. 若在上单调递增,则
11.英国数学家贝叶斯在概率论研究方面成就显著,根据贝叶斯统计理论,随机事件 存在如下关系:.某高校有甲 乙两家餐厅,王同学第一天去甲 乙两家餐厅就餐的概率分别为0.4和0.6.如果他第一天去甲餐厅,那么第二天去甲餐厅的概率为0.6;如果第一天去乙餐厅,那么第二天去甲餐厅的概率为0.5,则王同学( )
A.第二天去甲餐厅的概率为0.54
B.第二天去乙餐厅的概率为0.44
C.第二天去了甲餐厅,则第一天去乙餐厅的概率为
D.第二天去了乙餐厅,则第一天去甲餐厅的概率为
12.已知抛物线的焦点为,抛物线上的点到点的距离是2,是抛物线的准线与轴的交点,,是抛物线上两个不同的动点,为坐标原点,则( )
A. B.若直线过点,则
C.若直线过点,则 D.若直线过点,则
三、填空题:本题共4小题,每小题5分,共20分.
13.在的展开式中,常数项为______.
14.若,,则______.
15.知函数,,函数的图象在点和点的两条切线互相垂直,且分别与轴交于两点,则的取值范围是________.
16.张衡是中国东汉时期伟大的天文学家、数学家, 他曾在数学著作《算罔论》中得出结论:圆周率的平方除以十六约等于八分之五. 已知在菱形中,, 将沿进行翻折, 使得. 按张衡的结论, 三棱锥外接球的表面积约为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知数列满足,,,且.
(1)求数列的通项公式;
(2)若,求数列的前n项和.
18.△中,内角,,所对的边分别为,,,,.
(1)求;
(2)如图,点为边上一点,,,求△的面积.
19.如图,四边形为梯形,,四边形为平行四边形.
(1)求证:∥平面;
(2)若平面,求:
(ⅰ)直线与平面所成角的正弦值;
(ⅱ)点D到平面的距离.
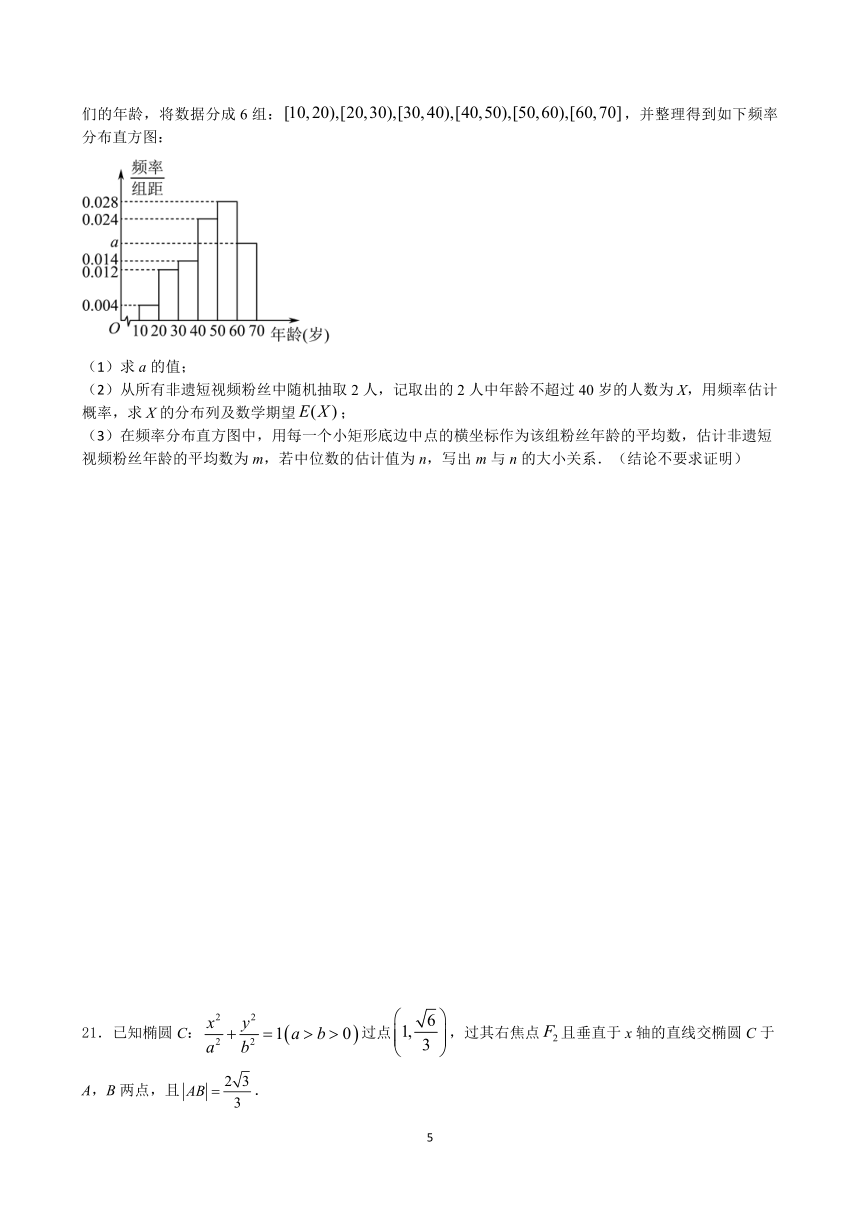
20.非物质文化遗产(简称“非遗”)是优秀传统文化的重要组成部分,是一个国家和民族历史文化成就的重要标志.随着短视频这一新兴媒介形态的兴起,非遗传播获得广阔的平台,非遗文化迎来了发展的春天.为研究非遗短视频受众的年龄结构,现从各短视频平台随机调查了1000名非遗短视频粉丝,记录他们的年龄,将数据分成6组:,并整理得到如下频率分布直方图:
(1)求a的值;
(2)从所有非遗短视频粉丝中随机抽取2人,记取出的2人中年龄不超过40岁的人数为X,用频率估计概率,求X的分布列及数学期望;
(3)在频率分布直方图中,用每一个小矩形底边中点的横坐标作为该组粉丝年龄的平均数,估计非遗短视频粉丝年龄的平均数为m,若中位数的估计值为n,写出m与n的大小关系.(结论不要求证明)
21.已知椭圆C:过点,过其右焦点且垂直于x轴的直线交椭圆C于A,B两点,且.
(1)求椭圆C的方程;
(2)若直线l:与椭圆C交于E,F两点,线段EF的中点为Q,在y轴上是否存在定点P,使得∠EQP=2∠EFP恒成立?若存在,求出点P的坐标;若不存在,请说明理由.
22.已知函数.
(1)若是的极值点,求a;
(2)若,分别是的零点和极值点,当时,证明:.
2022-2023学年高三数学下学期期初考试仿真模拟试卷04
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则集合的子集个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】因为,,
所以,
所以的子集为,共2个.
故选:B.
2.复数满足,则( )
A. B. C. D. 5
【答案】C
【解析】设(),由题意得,解得,,所以
故选:C
3.一个圆锥的侧面展开图恰好是一个半径为1的半圆,则该圆锥的表面积为( )
A. B. C. D.
【答案】A
【解析】依题意,设圆锥底面半径为,高为,母线长为,则,
底面周长为,则,所以,
所以圆锥的表面积为,
故选:A.
4.已知平面向量的夹角为,且,则( )
A. 4 B. 2 C. 1 D.
【答案】B
【解析】
因为向量的夹角为,且,
所以,
故选:B
5.某小区共有3个核酸检测点同时进行检测,有6名志愿者被分配到这3个检测点参加服务,6人中有4名“熟手”和2名“生手”,1名“生手”至少需要1名“熟手”进行检测工作的传授,每个检测点至少需要1名“熟手”,且2名“生手”不能分配到同一个检测点,则不同的分配方案种数是( )
A. 72 B. 108 C. 216 D. 432
【答案】C
【解析】根据题意,可先把4名“熟手”分为人数为的三组,再分配到3个检测点,共有种分法,然后把2名“生手”分配到3个检测点中的2个,有种分法,所以共有种不同的分配方案.
故选:C.
6.已知数列的前n项和组成的数列满足,,,则数列的通项公式为( )
A. B.
C. D.
【答案】C
【解析】因为,,
所以,,故可排除A,D;
又因为,
所以,
即,
又因为,
所以当时,数列是首项为4,公比为2的等比数列,
所以,
所以.
故选:C.
7.设,分别为双曲线(,)的左、右焦点,A为双曲线的左顶点,以为直径的圆交双曲线的某条渐近线于M,N两点,且,(如图),则该双曲线的离心率为( )
A. B. C. D.
【答案】A
【解析】不妨设圆与相交,且点的坐标为,
则点的坐标为,
联立,
得,
又且,
所以,
所以由余弦定理得:,
化简得,
所以,
所以.
故选:A
8.不等式在上恒成立,则实数的取值范围是( )
A. B. C. D.
【答案】B
【解析】当时,不等式在上恒成立不会成立,
故 ,
当 时, ,此时不等式恒成立;
不等式在上恒成立,
即在上恒成立,
而即,
设 ,当 时,,
故是增函数,
则即,故,
设,
当 时,, 递增,
当 时,, 递减,
故 ,则 ,
综合以上,实数的取值范围是 ,
故选:B
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知数据,,,…,的众数、平均数、方差、第80百分位数分别是,,,,数据,,,…,的众数、平均数、方差、第80百分位数分别是,,,,且满足,则下列结论正确的是( )
A. B.
C. D.
【答案】ACD
【解析】由题意可知,两组数据满足,
由平均数计算公式得,
所以,故A正确;
由它们的众数也满足,则有,故B错误;
由方差的性质得,故C正确;
对于数据,,,,,假设其第80百分位数为,
当是整数时,,
当不是整数时,设其整数部分为,则,
所以对于数据,,,,,假设其第80百分位数为,
当是整数时,,
当不是整数时,设其整数部分为,则,
所以,故D正确.
故选:ACD.
10.向量 函数,则下述结论正确的有( )
A. 若的图像关于直线对称,则可能为
B. 周期时,则的图像关于点对称
C. 若的图像向左平移个单位长度后得到一个偶函数,则的最小值为
D. 若在上单调递增,则
【答案】ACD
【解析】
,
对于A选项,若的图像关于直线对称,则,所以,当时,,故A正确;
对于B选项,当,则=2,令,,当时,,所以关于对称,故B错误;
对于C选项,若的图像向左平移个单位长度后得到,
所以,又,所以,故C正确;
对于D选项,因为函数在上递增,所以,故D正确.
故选:ACD.
11.英国数学家贝叶斯在概率论研究方面成就显著,根据贝叶斯统计理论,随机事件 存在如下关系:.某高校有甲 乙两家餐厅,王同学第一天去甲 乙两家餐厅就餐的概率分别为0.4和0.6.如果他第一天去甲餐厅,那么第二天去甲餐厅的概率为0.6;如果第一天去乙餐厅,那么第二天去甲餐厅的概率为0.5,则王同学( )
A.第二天去甲餐厅的概率为0.54
B.第二天去乙餐厅的概率为0.44
C.第二天去了甲餐厅,则第一天去乙餐厅的概率为
D.第二天去了乙餐厅,则第一天去甲餐厅的概率为
【答案】AC
【解析】设:第一天去甲餐厅,:第二天去甲餐厅,
:第一天去乙餐厅,:第二天去乙餐厅,
所以,,,
因为,
所以,
所以有,
因此选项A正确, ,因此选项B不正确;
因为,所以选项C正确;
,所以选项D不正确,
故选:AC
12.已知抛物线的焦点为,抛物线上的点到点的距离是2,是抛物线的准线与轴的交点,,是抛物线上两个不同的动点,为坐标原点,则( )
A. B.若直线过点,则
C.若直线过点,则 D.若直线过点,则
【答案】BCD
【解析】由题意得,则,故抛物线的方程为,
将代入抛物线的方程,得,解得,
所以A不正确;
设,,易知直线的斜率不为零,当直线过点时,
可设直线的方程为,与抛物线方程联立,得,
化简得:,则,,
所以,所以,
所以B正确;
易知,则由选项B得
,
所以直线平分,所以,
选项C正确;
因为直线过点,且斜率不为零,
所以设直线的方程为,与抛物线方程联立,
易得,所以.
因为,,且,
所以,又,所以,所以D正确.
故选:BCD.
三、填空题:本题共4小题,每小题5分,共20分.
13.在的展开式中,常数项为______.
【答案】24
【解析】二项式展开式的通项为,令,解得,所以展开式的常数项为
故答案为:24
14.若,,则______.
【答案】
【解析】由得,两边平方得,,解得或(,舍去),故
故答案为:
15.知函数,,函数的图象在点和点的两条切线互相垂直,且分别与轴交于两点,则的取值范围是________.
【答案】
【解析】当,时,
,,
在处的切线方程为,即,
;
当,,,
同理可求得:在处的切线方程为:,
,
两条切线互相垂直,,,,
令,
设,,
则在上单调递增,,即.
故答案为:.
16.张衡是中国东汉时期伟大的天文学家、数学家, 他曾在数学著作《算罔论》中得出结论:圆周率的平方除以十六约等于八分之五. 已知在菱形中,, 将沿进行翻折, 使得. 按张衡的结论, 三棱锥外接球的表面积约为______.
【答案】
【解析】如图1,
取BD的中点M,连接.由,可得为正三角形,且,所以,则,
以M为原点,为轴,为轴,过点M且与平面垂直的直线为轴建立空间直角坐标系如图2,
则, .设为三棱锥的外接球球心,则在平面的投影必为的外心,则设.由可得,解得,所以.
由张衡的结论,,所以,
则三棱锥的外接球表面积为,
故答案为:
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知数列满足,,,且.
(1)求数列的通项公式;
(2)若,求数列的前n项和.
【答案】(1), (2)
【解析】(1)因为,,,,
可得,,
又,
则当时,
,
上式对也成立,所以,;
(2)由,
可得,
则数列的前项和为
.
18.△中,内角,,所对的边分别为,,,,.
(1)求;
(2)如图,点为边上一点,,,求△的面积.
【答案】(1);(2).
【解析】(1)∵,即,
∴.
由正弦定理,得:,又,
∴,则,又且,
∴,则,
∴.
(2)由(1)有,易知为锐角,
由,则.
∵,故,则,
∴,
在△中,由正弦定理,得,
∴,.
又,
∴.
19.如图,四边形为梯形,,四边形为平行四边形.
(1)求证:∥平面;
(2)若平面,求:
(ⅰ)直线与平面所成角的正弦值;
(ⅱ)点D到平面的距离.
【答案】(1)见解析; (2)(i);(ii).
【解析】(1)如图,在射线上取点,使,连接.
由题设,得,所以四边形为平行四边形.
所以且.
又四边形为平行四边形,
所以且.
所以且..
所以四边形为平行四边形,
所以.
因为平面平面
所以平面.
(2)(i)因为平面,平面,
所以.又,
所以,,两两相互垂直.
如图建立空间直角坐标系,
则.所以.
设平面的法向量为,则
即
令,则.于是.
设直线与平面所成角为,则
所以直线与平面所成角的正弦值为.
(ii)因为,
所以直线与平面所成角的正弦值为.
所以点到平面的距离为
20.非物质文化遗产(简称“非遗”)是优秀传统文化的重要组成部分,是一个国家和民族历史文化成就的重要标志.随着短视频这一新兴媒介形态的兴起,非遗传播获得广阔的平台,非遗文化迎来了发展的春天.为研究非遗短视频受众的年龄结构,现从各短视频平台随机调查了1000名非遗短视频粉丝,记录他们的年龄,将数据分成6组:,并整理得到如下频率分布直方图:
(1)求a的值;
(2)从所有非遗短视频粉丝中随机抽取2人,记取出的2人中年龄不超过40岁的人数为X,用频率估计概率,求X的分布列及数学期望;
(3)在频率分布直方图中,用每一个小矩形底边中点的横坐标作为该组粉丝年龄的平均数,估计非遗短视频粉丝年龄的平均数为m,若中位数的估计值为n,写出m与n的大小关系.(结论不要求证明)
【答案】(1) (2)分布列详见解析, (3)
【解析】(1),
解得.
(2)不超过40岁的人的频率为,
所以,的可能取值为,
,
,
,
所以的分布列为:
所以.
(3)岁.
,
所以.
21.已知椭圆C:过点,过其右焦点且垂直于x轴的直线交椭圆C于A,B两点,且.
(1)求椭圆C的方程;
(2)若直线l:与椭圆C交于E,F两点,线段EF的中点为Q,在y轴上是否存在定点P,使得∠EQP=2∠EFP恒成立?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1) (2)存在定点,
【解析】(1)由题知,椭圆C过点和,
所以,解得
所以椭圆C的方程为.
(2)
假设在y轴上存在定点P,使得∠EQP=2∠EFP恒成立,设,,
由,得,∴,
∵∠EQP=2∠EFP,∴∠EFP=∠FPQ,∴QE=QF=QP
∴点P在以EF为直径的圆上,即PE⊥PF
,
∴
∴恒成立
∴,解得
∴
∴存在定点,使得∠EQP=2∠EFP恒成立.
22.已知函数.
(1)若是的极值点,求a;
(2)若,分别是的零点和极值点,当时,证明:.
【答案】(1) (2)证明见解析
【解析】(1)因为 所以
若是函数的极值点,则 ,即,
此时
设,则,,
所以存在,使得当时,,单调递减,
当时, ,单调递增,当时 ,单调递减,
所以当时,是的极值点.
(2)因为若,分别是的零点和极值点,所以 ,,
,,所以
当时, ,则,,即,,
因为 所以当 即 时,成立,
当 时,若,则只需证明,
设 ,则 ,
设,
则 为增函数,且,
所以存在唯一,使得 ,
当时,,单调递减,当时,,单调递增,
故, 所以,单调递增,
所以, 等价于.
设 ,则
当 时,若 时,,,单调递减,
所以当 ,,所以当 时成立,
设,则 ,
当时,,单调递增,所以当时,,
即 ,成立.
综上,若,分别是的零点和极值点,当时,有.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则集合的子集个数为( )
A. 1 B. 2 C. 3 D. 4
2.复数满足,则( )
A. B. C. D. 5
3.一个圆锥的侧面展开图恰好是一个半径为1的半圆,则该圆锥的表面积为( )
A. B. C. D.
4.已知平面向量的夹角为,且,则( )
A. 4 B. 2 C. 1 D.
5.某小区共有3个核酸检测点同时进行检测,有6名志愿者被分配到这3个检测点参加服务,6人中有4名“熟手”和2名“生手”,1名“生手”至少需要1名“熟手”进行检测工作的传授,每个检测点至少需要1名“熟手”,且2名“生手”不能分配到同一个检测点,则不同的分配方案种数是( )
A. 72 B. 108 C. 216 D. 432
6.已知数列的前n项和组成的数列满足,,,则数列的通项公式为( )
A. B.
C. D.
7.设,分别为双曲线(,)的左、右焦点,A为双曲线的左顶点,以为直径的圆交双曲线的某条渐近线于M,N两点,且,(如图),则该双曲线的离心率为( )
A. B. C. D.
8.不等式在上恒成立,则实数的取值范围是( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知数据,,,…,的众数、平均数、方差、第80百分位数分别是,,,,数据,,,…,的众数、平均数、方差、第80百分位数分别是,,,,且满足,则下列结论正确的是( )
A. B.
C. D.
10.向量 函数,则下述结论正确的有( )
A. 若的图像关于直线对称,则可能为
B. 周期时,则的图像关于点对称
C. 若的图像向左平移个单位长度后得到一个偶函数,则的最小值为
D. 若在上单调递增,则
11.英国数学家贝叶斯在概率论研究方面成就显著,根据贝叶斯统计理论,随机事件 存在如下关系:.某高校有甲 乙两家餐厅,王同学第一天去甲 乙两家餐厅就餐的概率分别为0.4和0.6.如果他第一天去甲餐厅,那么第二天去甲餐厅的概率为0.6;如果第一天去乙餐厅,那么第二天去甲餐厅的概率为0.5,则王同学( )
A.第二天去甲餐厅的概率为0.54
B.第二天去乙餐厅的概率为0.44
C.第二天去了甲餐厅,则第一天去乙餐厅的概率为
D.第二天去了乙餐厅,则第一天去甲餐厅的概率为
12.已知抛物线的焦点为,抛物线上的点到点的距离是2,是抛物线的准线与轴的交点,,是抛物线上两个不同的动点,为坐标原点,则( )
A. B.若直线过点,则
C.若直线过点,则 D.若直线过点,则
三、填空题:本题共4小题,每小题5分,共20分.
13.在的展开式中,常数项为______.
14.若,,则______.
15.知函数,,函数的图象在点和点的两条切线互相垂直,且分别与轴交于两点,则的取值范围是________.
16.张衡是中国东汉时期伟大的天文学家、数学家, 他曾在数学著作《算罔论》中得出结论:圆周率的平方除以十六约等于八分之五. 已知在菱形中,, 将沿进行翻折, 使得. 按张衡的结论, 三棱锥外接球的表面积约为______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知数列满足,,,且.
(1)求数列的通项公式;
(2)若,求数列的前n项和.
18.△中,内角,,所对的边分别为,,,,.
(1)求;
(2)如图,点为边上一点,,,求△的面积.
19.如图,四边形为梯形,,四边形为平行四边形.
(1)求证:∥平面;
(2)若平面,求:
(ⅰ)直线与平面所成角的正弦值;
(ⅱ)点D到平面的距离.
20.非物质文化遗产(简称“非遗”)是优秀传统文化的重要组成部分,是一个国家和民族历史文化成就的重要标志.随着短视频这一新兴媒介形态的兴起,非遗传播获得广阔的平台,非遗文化迎来了发展的春天.为研究非遗短视频受众的年龄结构,现从各短视频平台随机调查了1000名非遗短视频粉丝,记录他们的年龄,将数据分成6组:,并整理得到如下频率分布直方图:
(1)求a的值;
(2)从所有非遗短视频粉丝中随机抽取2人,记取出的2人中年龄不超过40岁的人数为X,用频率估计概率,求X的分布列及数学期望;
(3)在频率分布直方图中,用每一个小矩形底边中点的横坐标作为该组粉丝年龄的平均数,估计非遗短视频粉丝年龄的平均数为m,若中位数的估计值为n,写出m与n的大小关系.(结论不要求证明)
21.已知椭圆C:过点,过其右焦点且垂直于x轴的直线交椭圆C于A,B两点,且.
(1)求椭圆C的方程;
(2)若直线l:与椭圆C交于E,F两点,线段EF的中点为Q,在y轴上是否存在定点P,使得∠EQP=2∠EFP恒成立?若存在,求出点P的坐标;若不存在,请说明理由.
22.已知函数.
(1)若是的极值点,求a;
(2)若,分别是的零点和极值点,当时,证明:.
2022-2023学年高三数学下学期期初考试仿真模拟试卷04
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则集合的子集个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】因为,,
所以,
所以的子集为,共2个.
故选:B.
2.复数满足,则( )
A. B. C. D. 5
【答案】C
【解析】设(),由题意得,解得,,所以
故选:C
3.一个圆锥的侧面展开图恰好是一个半径为1的半圆,则该圆锥的表面积为( )
A. B. C. D.
【答案】A
【解析】依题意,设圆锥底面半径为,高为,母线长为,则,
底面周长为,则,所以,
所以圆锥的表面积为,
故选:A.
4.已知平面向量的夹角为,且,则( )
A. 4 B. 2 C. 1 D.
【答案】B
【解析】
因为向量的夹角为,且,
所以,
故选:B
5.某小区共有3个核酸检测点同时进行检测,有6名志愿者被分配到这3个检测点参加服务,6人中有4名“熟手”和2名“生手”,1名“生手”至少需要1名“熟手”进行检测工作的传授,每个检测点至少需要1名“熟手”,且2名“生手”不能分配到同一个检测点,则不同的分配方案种数是( )
A. 72 B. 108 C. 216 D. 432
【答案】C
【解析】根据题意,可先把4名“熟手”分为人数为的三组,再分配到3个检测点,共有种分法,然后把2名“生手”分配到3个检测点中的2个,有种分法,所以共有种不同的分配方案.
故选:C.
6.已知数列的前n项和组成的数列满足,,,则数列的通项公式为( )
A. B.
C. D.
【答案】C
【解析】因为,,
所以,,故可排除A,D;
又因为,
所以,
即,
又因为,
所以当时,数列是首项为4,公比为2的等比数列,
所以,
所以.
故选:C.
7.设,分别为双曲线(,)的左、右焦点,A为双曲线的左顶点,以为直径的圆交双曲线的某条渐近线于M,N两点,且,(如图),则该双曲线的离心率为( )
A. B. C. D.
【答案】A
【解析】不妨设圆与相交,且点的坐标为,
则点的坐标为,
联立,
得,
又且,
所以,
所以由余弦定理得:,
化简得,
所以,
所以.
故选:A
8.不等式在上恒成立,则实数的取值范围是( )
A. B. C. D.
【答案】B
【解析】当时,不等式在上恒成立不会成立,
故 ,
当 时, ,此时不等式恒成立;
不等式在上恒成立,
即在上恒成立,
而即,
设 ,当 时,,
故是增函数,
则即,故,
设,
当 时,, 递增,
当 时,, 递减,
故 ,则 ,
综合以上,实数的取值范围是 ,
故选:B
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知数据,,,…,的众数、平均数、方差、第80百分位数分别是,,,,数据,,,…,的众数、平均数、方差、第80百分位数分别是,,,,且满足,则下列结论正确的是( )
A. B.
C. D.
【答案】ACD
【解析】由题意可知,两组数据满足,
由平均数计算公式得,
所以,故A正确;
由它们的众数也满足,则有,故B错误;
由方差的性质得,故C正确;
对于数据,,,,,假设其第80百分位数为,
当是整数时,,
当不是整数时,设其整数部分为,则,
所以对于数据,,,,,假设其第80百分位数为,
当是整数时,,
当不是整数时,设其整数部分为,则,
所以,故D正确.
故选:ACD.
10.向量 函数,则下述结论正确的有( )
A. 若的图像关于直线对称,则可能为
B. 周期时,则的图像关于点对称
C. 若的图像向左平移个单位长度后得到一个偶函数,则的最小值为
D. 若在上单调递增,则
【答案】ACD
【解析】
,
对于A选项,若的图像关于直线对称,则,所以,当时,,故A正确;
对于B选项,当,则=2,令,,当时,,所以关于对称,故B错误;
对于C选项,若的图像向左平移个单位长度后得到,
所以,又,所以,故C正确;
对于D选项,因为函数在上递增,所以,故D正确.
故选:ACD.
11.英国数学家贝叶斯在概率论研究方面成就显著,根据贝叶斯统计理论,随机事件 存在如下关系:.某高校有甲 乙两家餐厅,王同学第一天去甲 乙两家餐厅就餐的概率分别为0.4和0.6.如果他第一天去甲餐厅,那么第二天去甲餐厅的概率为0.6;如果第一天去乙餐厅,那么第二天去甲餐厅的概率为0.5,则王同学( )
A.第二天去甲餐厅的概率为0.54
B.第二天去乙餐厅的概率为0.44
C.第二天去了甲餐厅,则第一天去乙餐厅的概率为
D.第二天去了乙餐厅,则第一天去甲餐厅的概率为
【答案】AC
【解析】设:第一天去甲餐厅,:第二天去甲餐厅,
:第一天去乙餐厅,:第二天去乙餐厅,
所以,,,
因为,
所以,
所以有,
因此选项A正确, ,因此选项B不正确;
因为,所以选项C正确;
,所以选项D不正确,
故选:AC
12.已知抛物线的焦点为,抛物线上的点到点的距离是2,是抛物线的准线与轴的交点,,是抛物线上两个不同的动点,为坐标原点,则( )
A. B.若直线过点,则
C.若直线过点,则 D.若直线过点,则
【答案】BCD
【解析】由题意得,则,故抛物线的方程为,
将代入抛物线的方程,得,解得,
所以A不正确;
设,,易知直线的斜率不为零,当直线过点时,
可设直线的方程为,与抛物线方程联立,得,
化简得:,则,,
所以,所以,
所以B正确;
易知,则由选项B得
,
所以直线平分,所以,
选项C正确;
因为直线过点,且斜率不为零,
所以设直线的方程为,与抛物线方程联立,
易得,所以.
因为,,且,
所以,又,所以,所以D正确.
故选:BCD.
三、填空题:本题共4小题,每小题5分,共20分.
13.在的展开式中,常数项为______.
【答案】24
【解析】二项式展开式的通项为,令,解得,所以展开式的常数项为
故答案为:24
14.若,,则______.
【答案】
【解析】由得,两边平方得,,解得或(,舍去),故
故答案为:
15.知函数,,函数的图象在点和点的两条切线互相垂直,且分别与轴交于两点,则的取值范围是________.
【答案】
【解析】当,时,
,,
在处的切线方程为,即,
;
当,,,
同理可求得:在处的切线方程为:,
,
两条切线互相垂直,,,,
令,
设,,
则在上单调递增,,即.
故答案为:.
16.张衡是中国东汉时期伟大的天文学家、数学家, 他曾在数学著作《算罔论》中得出结论:圆周率的平方除以十六约等于八分之五. 已知在菱形中,, 将沿进行翻折, 使得. 按张衡的结论, 三棱锥外接球的表面积约为______.
【答案】
【解析】如图1,
取BD的中点M,连接.由,可得为正三角形,且,所以,则,
以M为原点,为轴,为轴,过点M且与平面垂直的直线为轴建立空间直角坐标系如图2,
则, .设为三棱锥的外接球球心,则在平面的投影必为的外心,则设.由可得,解得,所以.
由张衡的结论,,所以,
则三棱锥的外接球表面积为,
故答案为:
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知数列满足,,,且.
(1)求数列的通项公式;
(2)若,求数列的前n项和.
【答案】(1), (2)
【解析】(1)因为,,,,
可得,,
又,
则当时,
,
上式对也成立,所以,;
(2)由,
可得,
则数列的前项和为
.
18.△中,内角,,所对的边分别为,,,,.
(1)求;
(2)如图,点为边上一点,,,求△的面积.
【答案】(1);(2).
【解析】(1)∵,即,
∴.
由正弦定理,得:,又,
∴,则,又且,
∴,则,
∴.
(2)由(1)有,易知为锐角,
由,则.
∵,故,则,
∴,
在△中,由正弦定理,得,
∴,.
又,
∴.
19.如图,四边形为梯形,,四边形为平行四边形.
(1)求证:∥平面;
(2)若平面,求:
(ⅰ)直线与平面所成角的正弦值;
(ⅱ)点D到平面的距离.
【答案】(1)见解析; (2)(i);(ii).
【解析】(1)如图,在射线上取点,使,连接.
由题设,得,所以四边形为平行四边形.
所以且.
又四边形为平行四边形,
所以且.
所以且..
所以四边形为平行四边形,
所以.
因为平面平面
所以平面.
(2)(i)因为平面,平面,
所以.又,
所以,,两两相互垂直.
如图建立空间直角坐标系,
则.所以.
设平面的法向量为,则
即
令,则.于是.
设直线与平面所成角为,则
所以直线与平面所成角的正弦值为.
(ii)因为,
所以直线与平面所成角的正弦值为.
所以点到平面的距离为
20.非物质文化遗产(简称“非遗”)是优秀传统文化的重要组成部分,是一个国家和民族历史文化成就的重要标志.随着短视频这一新兴媒介形态的兴起,非遗传播获得广阔的平台,非遗文化迎来了发展的春天.为研究非遗短视频受众的年龄结构,现从各短视频平台随机调查了1000名非遗短视频粉丝,记录他们的年龄,将数据分成6组:,并整理得到如下频率分布直方图:
(1)求a的值;
(2)从所有非遗短视频粉丝中随机抽取2人,记取出的2人中年龄不超过40岁的人数为X,用频率估计概率,求X的分布列及数学期望;
(3)在频率分布直方图中,用每一个小矩形底边中点的横坐标作为该组粉丝年龄的平均数,估计非遗短视频粉丝年龄的平均数为m,若中位数的估计值为n,写出m与n的大小关系.(结论不要求证明)
【答案】(1) (2)分布列详见解析, (3)
【解析】(1),
解得.
(2)不超过40岁的人的频率为,
所以,的可能取值为,
,
,
,
所以的分布列为:
所以.
(3)岁.
,
所以.
21.已知椭圆C:过点,过其右焦点且垂直于x轴的直线交椭圆C于A,B两点,且.
(1)求椭圆C的方程;
(2)若直线l:与椭圆C交于E,F两点,线段EF的中点为Q,在y轴上是否存在定点P,使得∠EQP=2∠EFP恒成立?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1) (2)存在定点,
【解析】(1)由题知,椭圆C过点和,
所以,解得
所以椭圆C的方程为.
(2)
假设在y轴上存在定点P,使得∠EQP=2∠EFP恒成立,设,,
由,得,∴,
∵∠EQP=2∠EFP,∴∠EFP=∠FPQ,∴QE=QF=QP
∴点P在以EF为直径的圆上,即PE⊥PF
,
∴
∴恒成立
∴,解得
∴
∴存在定点,使得∠EQP=2∠EFP恒成立.
22.已知函数.
(1)若是的极值点,求a;
(2)若,分别是的零点和极值点,当时,证明:.
【答案】(1) (2)证明见解析
【解析】(1)因为 所以
若是函数的极值点,则 ,即,
此时
设,则,,
所以存在,使得当时,,单调递减,
当时, ,单调递增,当时 ,单调递减,
所以当时,是的极值点.
(2)因为若,分别是的零点和极值点,所以 ,,
,,所以
当时, ,则,,即,,
因为 所以当 即 时,成立,
当 时,若,则只需证明,
设 ,则 ,
设,
则 为增函数,且,
所以存在唯一,使得 ,
当时,,单调递减,当时,,单调递增,
故, 所以,单调递增,
所以, 等价于.
设 ,则
当 时,若 时,,,单调递减,
所以当 ,,所以当 时成立,
设,则 ,
当时,,单调递增,所以当时,,
即 ,成立.
综上,若,分别是的零点和极值点,当时,有.
同课章节目录
