2022-2023学年北师大版九年级数学下册 2.2二次函数的图像与性质综合练习(无答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学下册 2.2二次函数的图像与性质综合练习(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 375.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 00:00:00 | ||
图片预览



文档简介
2.2二次函数的图像与性质综合练习
班级:________ 姓名:________
一、单选题(共 10 小题)
1、已知二次函数,关于该函数在的取值范围内,下列说法正确的是( ).
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
2、将抛物线C1:y=(x-3)2+2向左平移3个单位长度,得到抛物线C2,抛物线C2与抛物线C3关于x轴对称,则抛物线C3的解析式为( ).
A.y=x2-2 B.y=-x2+2 C.y=x2+2 D.y=-x2-2
3、已知:二次函数,将该二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新函数,当直线与新图象有2个交点时,的取值范围是( )
A. B.或 C.或 D.
4、一次函数与二次函数在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
5、关于二次函数y=-(x -2)2+3,以下说法正确的是( )
A.当x>-2时,y随x增大而减小 B.当x>-2时,y随x增大而增大
C.当x>2时,y随x增大而减小 D.当x>2时,y随x增大而增大
6、如图,正方形OABC的顶点B在抛物线y=的第一象限的图象上,若点B的横坐标与纵坐标之和等于6,则对角线AC的长为( )
A.2 B. C. D.
7、二次函数的图象过四个点,下列说法一定正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8、已知抛物线经过点,且该抛物线的对称轴经过点A,则该抛物线的解析式为( )
A. B. C. D.
9、已知二次函数(h为常数),当自变量x的值满足1≤x≤3时,其对应的函数值y的最小值为1,则h的值为( )
A.2或4 B.0或4 C.2或3 D.0或3
10、已知二次函数y=a(x﹣1)2﹣4,当﹣1≤x≤4时,y的最大值是5,则a的值是( )
A.﹣1 B.﹣2 C.1 D.2
二、填空题(共 10 小题)
1、己知抛物线,经过四点,则与的大小关系是_______.(填“>”“<”或“=”)
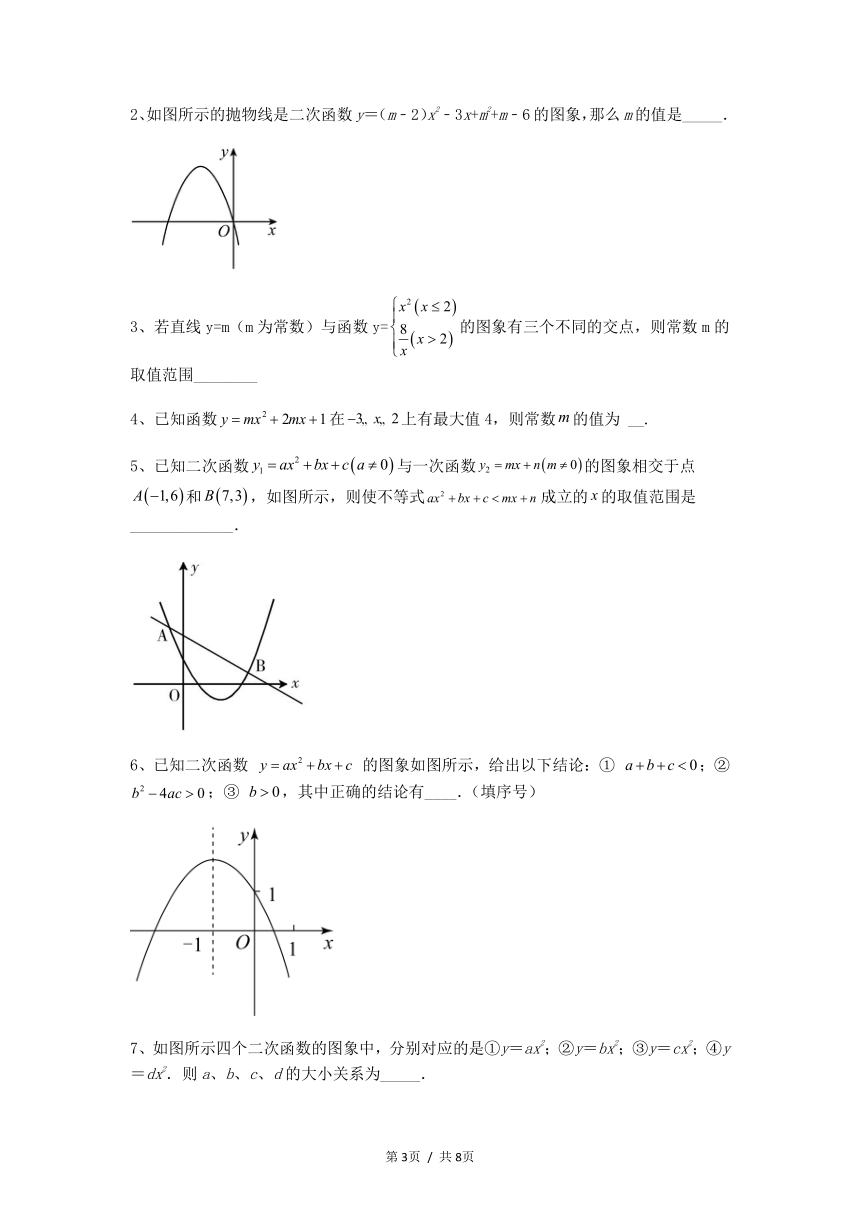
2、如图所示的抛物线是二次函数y=(m﹣2)x2﹣3x+m2+m﹣6的图象,那么m的值是_____.
3、若直线y=m(m为常数)与函数y=的图象有三个不同的交点,则常数m的取值范围________
4、已知函数在上有最大值4,则常数的值为 __.
5、已知二次函数与一次函数的图象相交于点和,如图所示,则使不等式成立的的取值范围是_____________.
6、已知二次函数 的图象如图所示,给出以下结论:① ;② ;③ ,其中正确的结论有____.(填序号)
7、如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为_____.
8、已知二次函数(是常数,)的与的部分对应值如下表:
0 2
6 0 6
下列结论:
①;
②当时,函数最小值为;
③若点,点在二次函数图象上,则;
④方程有两个不相等的实数根.
其中,正确结论的序号是__________________.(把所有正确结论的序号都填上)
9、如图,在矩形 ABCD 中,AD=3,点E是AD边上的动点,连接CE,以CE为边向右上方作正方形CEFG,过点F作 FH⊥AD,垂足为H,连接AF. 在整个变化过程中,△AEF 面积的最大值是_______.
10、当x=x1和x= x2(x1≠x2)时,二次函数y=3x2﹣3x+4的函数值相等、当x=x1+x2时,函数值是_________.
三、解答题(共 6 小题)
1、已知关于的一元二次方程,有两个不相等的实数根,.
(1)求的取值范围;
(2)当时,解这个方程;
(3)若,是方程的两个实数根,设,试求的最小值.
2、在平面直角坐标系中,如果一个点的横坐标与纵坐标互为相反数,则称该点为“黎点”.例如,都是“黎点”.
(1)求双曲线上的“黎点”;
(2)若抛物线(a、c为常数)上有且只有一个“黎点”,当时,求c的取值范围.
3、已知二次函数y=﹣(x+4)2,将此函数的图像向右平移3个单位长度,再向上平移2个单位长度.
(1)请写出平移后图像所对应的函数解析式;
(2)在如图所示的平面直角坐标系中,画出平移后的图像;
(3)根据所画的函数图像,写出当y<0时x的取值范围.
4、我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于直线(n为常数)对称,则把该函数称之为“函数”.
(1)在下列关于x的函数中,是“函数”的是________(填序号);
①,②,③
(2)若关于x的函数(h为常数)是“函数”,与(m为常数,)相交于A(,)、B(,)两点,A在B的左边,,求m的值;
(3)若关于x的“函数”(a,b为常数)经过点(,1),且,当时,函数的最大值为,最小值为,且,求t的值.
5、如图所示,已知二次函数的图象与x轴的一个交点为A(3,0),另一个交点为B,与y轴的交点为点C.
(1)求m的值;
(2)若经过点B的一次函数平分△的面积.求k、b的值.
6、如图,点在抛物线C:上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为,.平移该胶片,使所在抛物线对应的函数恰为.求点移动的最短路程.
第1页 / 共9页
班级:________ 姓名:________
一、单选题(共 10 小题)
1、已知二次函数,关于该函数在的取值范围内,下列说法正确的是( ).
A.有最大值-1,有最小值-2 B.有最大值0,有最小值-1
C.有最大值7,有最小值-1 D.有最大值7,有最小值-2
2、将抛物线C1:y=(x-3)2+2向左平移3个单位长度,得到抛物线C2,抛物线C2与抛物线C3关于x轴对称,则抛物线C3的解析式为( ).
A.y=x2-2 B.y=-x2+2 C.y=x2+2 D.y=-x2-2
3、已知:二次函数,将该二次函数在轴上方的图象沿轴翻折到轴下方,图象的其余部分不变,得到一个新函数,当直线与新图象有2个交点时,的取值范围是( )
A. B.或 C.或 D.
4、一次函数与二次函数在同一平面直角坐标系中的大致图象可能是( )
A. B.
C. D.
5、关于二次函数y=-(x -2)2+3,以下说法正确的是( )
A.当x>-2时,y随x增大而减小 B.当x>-2时,y随x增大而增大
C.当x>2时,y随x增大而减小 D.当x>2时,y随x增大而增大
6、如图,正方形OABC的顶点B在抛物线y=的第一象限的图象上,若点B的横坐标与纵坐标之和等于6,则对角线AC的长为( )
A.2 B. C. D.
7、二次函数的图象过四个点,下列说法一定正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
8、已知抛物线经过点,且该抛物线的对称轴经过点A,则该抛物线的解析式为( )
A. B. C. D.
9、已知二次函数(h为常数),当自变量x的值满足1≤x≤3时,其对应的函数值y的最小值为1,则h的值为( )
A.2或4 B.0或4 C.2或3 D.0或3
10、已知二次函数y=a(x﹣1)2﹣4,当﹣1≤x≤4时,y的最大值是5,则a的值是( )
A.﹣1 B.﹣2 C.1 D.2
二、填空题(共 10 小题)
1、己知抛物线,经过四点,则与的大小关系是_______.(填“>”“<”或“=”)
2、如图所示的抛物线是二次函数y=(m﹣2)x2﹣3x+m2+m﹣6的图象,那么m的值是_____.
3、若直线y=m(m为常数)与函数y=的图象有三个不同的交点,则常数m的取值范围________
4、已知函数在上有最大值4,则常数的值为 __.
5、已知二次函数与一次函数的图象相交于点和,如图所示,则使不等式成立的的取值范围是_____________.
6、已知二次函数 的图象如图所示,给出以下结论:① ;② ;③ ,其中正确的结论有____.(填序号)
7、如图所示四个二次函数的图象中,分别对应的是①y=ax2;②y=bx2;③y=cx2;④y=dx2.则a、b、c、d的大小关系为_____.
8、已知二次函数(是常数,)的与的部分对应值如下表:
0 2
6 0 6
下列结论:
①;
②当时,函数最小值为;
③若点,点在二次函数图象上,则;
④方程有两个不相等的实数根.
其中,正确结论的序号是__________________.(把所有正确结论的序号都填上)
9、如图,在矩形 ABCD 中,AD=3,点E是AD边上的动点,连接CE,以CE为边向右上方作正方形CEFG,过点F作 FH⊥AD,垂足为H,连接AF. 在整个变化过程中,△AEF 面积的最大值是_______.
10、当x=x1和x= x2(x1≠x2)时,二次函数y=3x2﹣3x+4的函数值相等、当x=x1+x2时,函数值是_________.
三、解答题(共 6 小题)
1、已知关于的一元二次方程,有两个不相等的实数根,.
(1)求的取值范围;
(2)当时,解这个方程;
(3)若,是方程的两个实数根,设,试求的最小值.
2、在平面直角坐标系中,如果一个点的横坐标与纵坐标互为相反数,则称该点为“黎点”.例如,都是“黎点”.
(1)求双曲线上的“黎点”;
(2)若抛物线(a、c为常数)上有且只有一个“黎点”,当时,求c的取值范围.
3、已知二次函数y=﹣(x+4)2,将此函数的图像向右平移3个单位长度,再向上平移2个单位长度.
(1)请写出平移后图像所对应的函数解析式;
(2)在如图所示的平面直角坐标系中,画出平移后的图像;
(3)根据所画的函数图像,写出当y<0时x的取值范围.
4、我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两点关于直线(n为常数)对称,则把该函数称之为“函数”.
(1)在下列关于x的函数中,是“函数”的是________(填序号);
①,②,③
(2)若关于x的函数(h为常数)是“函数”,与(m为常数,)相交于A(,)、B(,)两点,A在B的左边,,求m的值;
(3)若关于x的“函数”(a,b为常数)经过点(,1),且,当时,函数的最大值为,最小值为,且,求t的值.
5、如图所示,已知二次函数的图象与x轴的一个交点为A(3,0),另一个交点为B,与y轴的交点为点C.
(1)求m的值;
(2)若经过点B的一次函数平分△的面积.求k、b的值.
6、如图,点在抛物线C:上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为,.平移该胶片,使所在抛物线对应的函数恰为.求点移动的最短路程.
第1页 / 共9页
