2022-2023学年浙教版数学九年级下学期开学能力检测模式试题(一) (含解析)
文档属性
| 名称 | 2022-2023学年浙教版数学九年级下学期开学能力检测模式试题(一) (含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-30 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2022-2023学年浙教版数学九年级下学期
开学能力检测模式试题(一)
一、单选题(共10题;共30分)
1.(3分)若x的平方等于3,则x等于( )
A. B.9 C.或 D.9或-9
2.(3分)已知数a,b,c的大小关系如图所示,则下列各式:
①;②;③;④,其中正确个数是( )
A.1 B.2 C.3 D.4
3.(3分)下列分解因式正确的是( )
A. B.
C. D.
4.(3分)如图的四个三角形中,与全等的是( )
A. B.
C. D.
5.(3分)如图,把△ABC沿AC方向平移2cm得到△FDE,AE=7cm,则FC的长是( )cm
A.2 B.3 C.4 D.5
6.(3分)若a、b、c、d是正整数,且a+b=20,a+c=24,a+d=22,设a+b+c+d的最大值为M,最小值为N,则M﹣N=( )
A.28 B.12 C.48 D.36
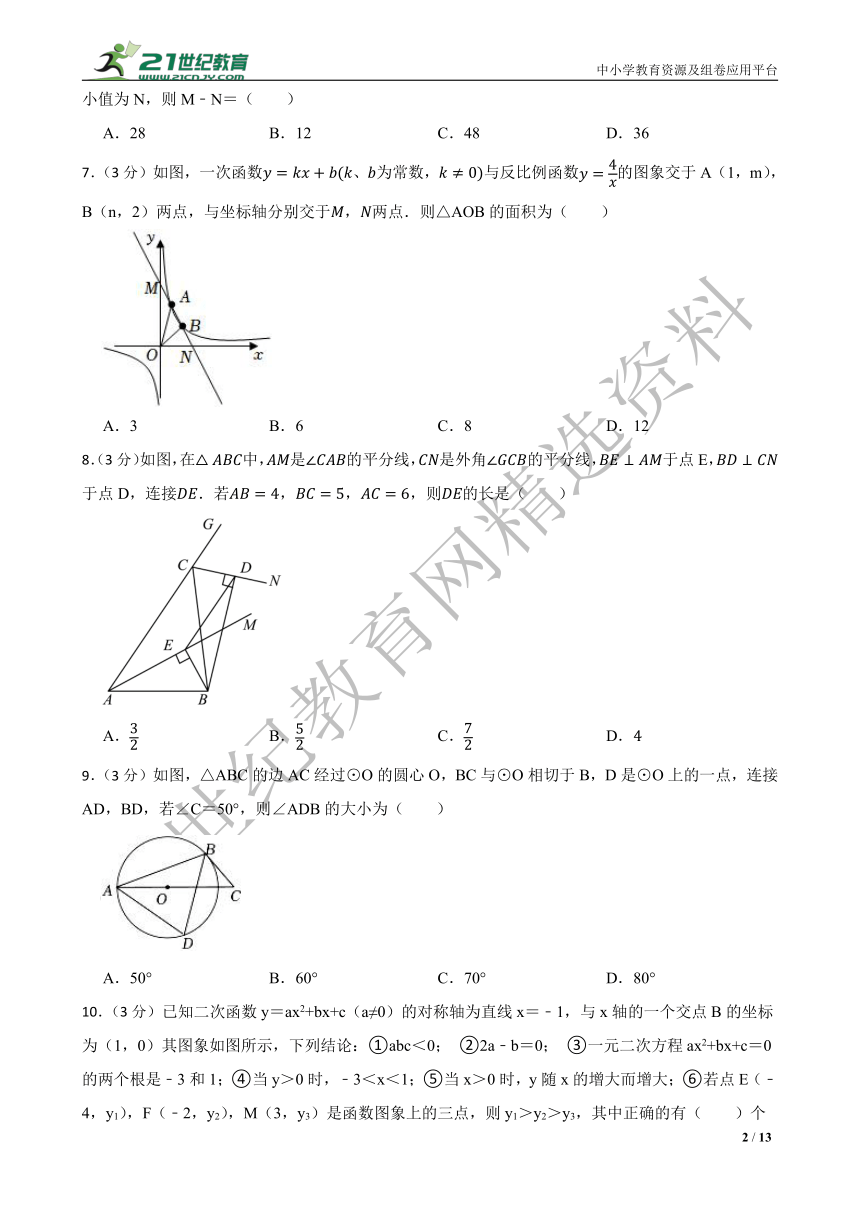
7.(3分)如图,一次函数、为常数,与反比例函数的图象交于A(1,m),B(n,2)两点,与坐标轴分别交于,两点.则△AOB的面积为( )
A.3 B.6 C.8 D.12
8.(3分)如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接.若,,,则的长是( )
A. B. C. D.
9.(3分)如图,△ABC的边AC经过⊙O的圆心O,BC与⊙O相切于B,D是⊙O上的一点,连接AD,BD,若∠C=50°,则∠ADB的大小为( )
A.50° B.60° C.70° D.80°
10.(3分)已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc<0; ②2a﹣b=0; ③一元二次方程ax2+bx+c=0的两个根是﹣3和1;④当y>0时,﹣3<x<1;⑤当x>0时,y随x的增大而增大;⑥若点E(﹣4,y1),F(﹣2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3,其中正确的有( )个
A.5 B.4 C.3 D.2
二、填空题(共6题;共24分)
11.(4分)若与最简二次根式是同类二次根式,则 .
12.(4分)某一天,小林与小李都要去核酸检测点进行核酸检测,若当地共有A,B,C,D四个核酸检测点,则在随机选择的情况下,两人都在同一检测点进行检测的概率是 .
13.(4分)若不等式组的解集中共有3个整数解,则a的取值范围是 .
14.(4分)某校要从甲、乙两名同学中选取一名成绩稳定的同学去参加数学竞赛,已知五次模拟测试中统计所得的信息为=115,S甲2=12,=115,S乙2=36,则应选择 参加竞赛.
15.(4分)在平面坐标系中点与点关于y轴对称,则 .
16.(4分)已知,,若的一边EF∥BC,则另一边DE与直线AB相交于点P,且点E不在直线AB上,则的度数为 .
三、解答题(共7题;共66分)
17.(5分)已知:如图,BD⊥AC于点D,EF⊥AC于点F,∠1+∠2=180°.求证:DGBC.
18.(6分)1号探测气球从海拔5m出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都上升了1小时.
(1)(3分)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间t(单位:min)的函数关系;
(2)(3分)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多少时间?位于什么高度?
19.(10分)小明在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组 频数 百分比
2 5%
6 15%
a 45%
9 22.5%
b c
2 d
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)(1分)频数分布表中: , , , .
(2)(3分)补全频数分布直方图.
(3)(3分)估计该居民小区家庭属于中等收入(不低于1000不足1600元)的大约有多少户?
20.(10分)在几何探究问题中,经常需要通过作辅助线(如,连接两点,过某点作垂线,作延长线,作平行线等等)把分散的条件相对集中,以达到解决问题的目的.
(1)(2分)(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上, ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为 (直接写出结果).
(2)(4分)(验证猜想)同学们讨论得出下列三种证明思路(如图1):
思路一:过点A作 ,交CD的延长线于点G.
思路二:过点A作 ,并截取 ,连接DG.
思路三:延长CD至点G,使 ,连接AG.
请选择你喜欢的一种思路证明(探究发现)中的结论.
(3)(4分)(迁移应用)如图2,点E,F分别在正方形ABCD的边BC,CD上,且 , ,设 ,试用含 的代数式表示DF的长.
21.(12分)如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
Ⅰ 试确定上述反比例函数和一次函数的表达式;
Ⅱ 连OB,在x轴上取点C,使 ,并求 的面积;
Ⅲ 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
22.(11分)如图,将两个等腰直角三角形纸片 和 放置在平面直角坐标系中,点 ,点 ,点 ,点 ,点 .
(1)(4分)求证: ;
(2)(3分)如图,现将 绕点O顺时针方向旋转,旋转角为 ,连接 , ,这一过程中 和 是否仍然保持相等?说明理由;当旋转角 的度数为 时, 所在直线能够垂直平分 ;
(3)(4分)在(2)的情况下,将旋转角 的范围扩大为 ,那么在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.(直接写出结果即可).
23.(12分)如图,已知:关于y的二次函数 的图象与x轴交于点 和点B,与y轴交于点 ,抛物线的对称轴与x轴交于点D.
(1)(4分)求二次函数的表达式.
(2)(4分)在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.
(3)(4分)有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】B
11.【答案】
12.【答案】
13.【答案】﹣3≤a<﹣2
14.【答案】甲
15.【答案】
16.【答案】10°或110°或70°或170°
17.【答案】证明:∵BD⊥AC,EF⊥AC,
∴∠BDC=∠EFC=90°.
∴BDEF.
∴∠2+∠DBE =180°.
∵∠1+∠2=180°,
∴∠1=∠DBE.
∴DGBC.
18.【答案】(1)解:根据题意得:1号探测气球所在位置的海拔:y1=t+5,2号探测气球所在位置的海拔:y2=0.5t+15;
(2)解:两个气球能位于同一高度,
根据题意得:t+5=0.5t+15,
解得:t=20,有t+5=25.
答:此时,气球上升了20分钟,都位于海拔25米的高度.
19.【答案】(1)18;3;7.5%;5%
(2)解:补全后的频数分布直方图如下所示:
(3)解:(户).
答:估计该居民小区家庭属于中等收入的大约有450户.
20.【答案】(1)EF=BE+DF
(2)解:过点A作 ,交CD的延长线于点G.
在正方形ABCD中, , ,
∴ , ,
∴ ,
∴ , ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ .
∴ ,
∴
(3)解:连接EF,设DF的长为 ,
∵BE=a,
∴ ,
∴ ,
根据【验证猜想】可得 ,
在 中,根据勾股定理得,
,
∴ ,即DF的长为
21.【答案】解:(Ⅰ)∵把A(-2,1)代入y= 得:m=-2×1=-2,
∴y=- ;
∵把B(1,n)代入y=- 得:n=-2,
∴B(1,-2),
∵把A、B的坐标代入y=kx+b得: ,
∴ ,
∴y=-x-1.
答:反比例函数的表达式是y=- ,一次函数的表达式是y=-x-1.
(Ⅱ)作BD⊥x轴于D,
∵BO=BC,
∴OD=DC.
∴D(1,0),C(2,0)
∴S△OBC= ×2×2=2.
(Ⅲ)一次函数值大于反比例函数值的自变量x的取值范围是:x<-2或0<x<1 .
22.【答案】(1)证明:(Ⅰ)∵ , , , ,
, , , ,
∴ , ,
∴
(2)90°
(3)解:
的底AB长度是固定的,所以要使它面积最大,则点D到AB的距离要最大,
已知点D的运动轨迹是一个圆,只要求出点O到AB的距离加上半径即可,
如图,过点O作 于点F,
,
则点D到AB的最大距离是: ,
∴ ,
是等腰直角三角形, ,
,
则此时 ,
故 的面积的最大值为 ,旋转角α的度数为 .
23.【答案】(1)解:把A(2,0)和C(0,6)代入y=x2+bx+c,
解得: ,
∴二次函数的表达式为:y=x2﹣5x+6;
(2)令y=0,则x2﹣5x+6=0,
解得:x=2或x=3,
∴B(3,0),抛物线对称轴是x= ,
∴BC2=32+62=45,
设P点坐标为(0,m),
CP2=(6-m)2,BP2=32+m2=9+ m2,
当∠CBP=90°时,BC2+ BP2= CP2,
45+9+m2=(6-m)2,
解得,m= ,P点坐标为(0, );
当∠CPB=90°时, CP2+ BP2= BC2,
45=9+m2+(6-m)2,
解得,m1=0,m2=6(舍去),P点坐标为(0,0);
综上所述,点P的坐标为:(0, )或(0,0);
(3)如图2,
设A运动时间为t,由AB=1,得BM=1﹣t,则DN=2t,
∴S△MNB= ×(1﹣t)×2t=﹣t2+t=﹣(t﹣ )2+ ,
当t= 时,S△MNB面积最大,最大面积为 ;
即当M( ,0)、N( ,1)或( ,﹣1)时△MNB面积最大,最大面积是 .
1 / 1
2022-2023学年浙教版数学九年级下学期
开学能力检测模式试题(一)
一、单选题(共10题;共30分)
1.(3分)若x的平方等于3,则x等于( )
A. B.9 C.或 D.9或-9
2.(3分)已知数a,b,c的大小关系如图所示,则下列各式:
①;②;③;④,其中正确个数是( )
A.1 B.2 C.3 D.4
3.(3分)下列分解因式正确的是( )
A. B.
C. D.
4.(3分)如图的四个三角形中,与全等的是( )
A. B.
C. D.
5.(3分)如图,把△ABC沿AC方向平移2cm得到△FDE,AE=7cm,则FC的长是( )cm
A.2 B.3 C.4 D.5
6.(3分)若a、b、c、d是正整数,且a+b=20,a+c=24,a+d=22,设a+b+c+d的最大值为M,最小值为N,则M﹣N=( )
A.28 B.12 C.48 D.36
7.(3分)如图,一次函数、为常数,与反比例函数的图象交于A(1,m),B(n,2)两点,与坐标轴分别交于,两点.则△AOB的面积为( )
A.3 B.6 C.8 D.12
8.(3分)如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接.若,,,则的长是( )
A. B. C. D.
9.(3分)如图,△ABC的边AC经过⊙O的圆心O,BC与⊙O相切于B,D是⊙O上的一点,连接AD,BD,若∠C=50°,则∠ADB的大小为( )
A.50° B.60° C.70° D.80°
10.(3分)已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc<0; ②2a﹣b=0; ③一元二次方程ax2+bx+c=0的两个根是﹣3和1;④当y>0时,﹣3<x<1;⑤当x>0时,y随x的增大而增大;⑥若点E(﹣4,y1),F(﹣2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3,其中正确的有( )个
A.5 B.4 C.3 D.2
二、填空题(共6题;共24分)
11.(4分)若与最简二次根式是同类二次根式,则 .
12.(4分)某一天,小林与小李都要去核酸检测点进行核酸检测,若当地共有A,B,C,D四个核酸检测点,则在随机选择的情况下,两人都在同一检测点进行检测的概率是 .
13.(4分)若不等式组的解集中共有3个整数解,则a的取值范围是 .
14.(4分)某校要从甲、乙两名同学中选取一名成绩稳定的同学去参加数学竞赛,已知五次模拟测试中统计所得的信息为=115,S甲2=12,=115,S乙2=36,则应选择 参加竞赛.
15.(4分)在平面坐标系中点与点关于y轴对称,则 .
16.(4分)已知,,若的一边EF∥BC,则另一边DE与直线AB相交于点P,且点E不在直线AB上,则的度数为 .
三、解答题(共7题;共66分)
17.(5分)已知:如图,BD⊥AC于点D,EF⊥AC于点F,∠1+∠2=180°.求证:DGBC.
18.(6分)1号探测气球从海拔5m出发,以1m/min的速度上升,与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升,两个气球都上升了1小时.
(1)(3分)用式子分别表示两个气球所在位置的海拔y(单位:m)关于上升时间t(单位:min)的函数关系;
(2)(3分)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多少时间?位于什么高度?
19.(10分)小明在学校组织的社会调查活动中负责了解他所居住的小区600户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组 频数 百分比
2 5%
6 15%
a 45%
9 22.5%
b c
2 d
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)(1分)频数分布表中: , , , .
(2)(3分)补全频数分布直方图.
(3)(3分)估计该居民小区家庭属于中等收入(不低于1000不足1600元)的大约有多少户?
20.(10分)在几何探究问题中,经常需要通过作辅助线(如,连接两点,过某点作垂线,作延长线,作平行线等等)把分散的条件相对集中,以达到解决问题的目的.
(1)(2分)(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上, ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为 (直接写出结果).
(2)(4分)(验证猜想)同学们讨论得出下列三种证明思路(如图1):
思路一:过点A作 ,交CD的延长线于点G.
思路二:过点A作 ,并截取 ,连接DG.
思路三:延长CD至点G,使 ,连接AG.
请选择你喜欢的一种思路证明(探究发现)中的结论.
(3)(4分)(迁移应用)如图2,点E,F分别在正方形ABCD的边BC,CD上,且 , ,设 ,试用含 的代数式表示DF的长.
21.(12分)如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
Ⅰ 试确定上述反比例函数和一次函数的表达式;
Ⅱ 连OB,在x轴上取点C,使 ,并求 的面积;
Ⅲ 直接写出一次函数值大于反比例函数值的自变量x的取值范围.
22.(11分)如图,将两个等腰直角三角形纸片 和 放置在平面直角坐标系中,点 ,点 ,点 ,点 ,点 .
(1)(4分)求证: ;
(2)(3分)如图,现将 绕点O顺时针方向旋转,旋转角为 ,连接 , ,这一过程中 和 是否仍然保持相等?说明理由;当旋转角 的度数为 时, 所在直线能够垂直平分 ;
(3)(4分)在(2)的情况下,将旋转角 的范围扩大为 ,那么在旋转过程中,求 的面积的最大值,并写出此时旋转角 的度数.(直接写出结果即可).
23.(12分)如图,已知:关于y的二次函数 的图象与x轴交于点 和点B,与y轴交于点 ,抛物线的对称轴与x轴交于点D.
(1)(4分)求二次函数的表达式.
(2)(4分)在y轴上是否存在一点P,使 为直角三角形.若存在,请求出点P的坐标.
(3)(4分)有一个点M从点A出发,以每秒1个单位的速度在 上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达B点时,点M、N同时停止运动,问点M、N运动到何处时, 面积最大,试求出面积.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】A
8.【答案】C
9.【答案】C
10.【答案】B
11.【答案】
12.【答案】
13.【答案】﹣3≤a<﹣2
14.【答案】甲
15.【答案】
16.【答案】10°或110°或70°或170°
17.【答案】证明:∵BD⊥AC,EF⊥AC,
∴∠BDC=∠EFC=90°.
∴BDEF.
∴∠2+∠DBE =180°.
∵∠1+∠2=180°,
∴∠1=∠DBE.
∴DGBC.
18.【答案】(1)解:根据题意得:1号探测气球所在位置的海拔:y1=t+5,2号探测气球所在位置的海拔:y2=0.5t+15;
(2)解:两个气球能位于同一高度,
根据题意得:t+5=0.5t+15,
解得:t=20,有t+5=25.
答:此时,气球上升了20分钟,都位于海拔25米的高度.
19.【答案】(1)18;3;7.5%;5%
(2)解:补全后的频数分布直方图如下所示:
(3)解:(户).
答:估计该居民小区家庭属于中等收入的大约有450户.
20.【答案】(1)EF=BE+DF
(2)解:过点A作 ,交CD的延长线于点G.
在正方形ABCD中, , ,
∴ , ,
∴ ,
∴ , ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ .
∴ ,
∴
(3)解:连接EF,设DF的长为 ,
∵BE=a,
∴ ,
∴ ,
根据【验证猜想】可得 ,
在 中,根据勾股定理得,
,
∴ ,即DF的长为
21.【答案】解:(Ⅰ)∵把A(-2,1)代入y= 得:m=-2×1=-2,
∴y=- ;
∵把B(1,n)代入y=- 得:n=-2,
∴B(1,-2),
∵把A、B的坐标代入y=kx+b得: ,
∴ ,
∴y=-x-1.
答:反比例函数的表达式是y=- ,一次函数的表达式是y=-x-1.
(Ⅱ)作BD⊥x轴于D,
∵BO=BC,
∴OD=DC.
∴D(1,0),C(2,0)
∴S△OBC= ×2×2=2.
(Ⅲ)一次函数值大于反比例函数值的自变量x的取值范围是:x<-2或0<x<1 .
22.【答案】(1)证明:(Ⅰ)∵ , , , ,
, , , ,
∴ , ,
∴
(2)90°
(3)解:
的底AB长度是固定的,所以要使它面积最大,则点D到AB的距离要最大,
已知点D的运动轨迹是一个圆,只要求出点O到AB的距离加上半径即可,
如图,过点O作 于点F,
,
则点D到AB的最大距离是: ,
∴ ,
是等腰直角三角形, ,
,
则此时 ,
故 的面积的最大值为 ,旋转角α的度数为 .
23.【答案】(1)解:把A(2,0)和C(0,6)代入y=x2+bx+c,
解得: ,
∴二次函数的表达式为:y=x2﹣5x+6;
(2)令y=0,则x2﹣5x+6=0,
解得:x=2或x=3,
∴B(3,0),抛物线对称轴是x= ,
∴BC2=32+62=45,
设P点坐标为(0,m),
CP2=(6-m)2,BP2=32+m2=9+ m2,
当∠CBP=90°时,BC2+ BP2= CP2,
45+9+m2=(6-m)2,
解得,m= ,P点坐标为(0, );
当∠CPB=90°时, CP2+ BP2= BC2,
45=9+m2+(6-m)2,
解得,m1=0,m2=6(舍去),P点坐标为(0,0);
综上所述,点P的坐标为:(0, )或(0,0);
(3)如图2,
设A运动时间为t,由AB=1,得BM=1﹣t,则DN=2t,
∴S△MNB= ×(1﹣t)×2t=﹣t2+t=﹣(t﹣ )2+ ,
当t= 时,S△MNB面积最大,最大面积为 ;
即当M( ,0)、N( ,1)或( ,﹣1)时△MNB面积最大,最大面积是 .
1 / 1
同课章节目录
