8.2.2 不等式的简单变形 教案

中小学教育资源及组卷应用平台
8.2.2 不等式的简单变形 教学设计
课题 8.2.2 不等式的简单变形 单元 第8 单元 学科 数学 年级 七年级（下）
教材分析 理解并掌握不等式的性质..在自主探索的基础上，由方程的基本变形得到不等式的基本性质.直接应用一次不等式的变形求解一元一次不等式，并指导学生掌握基本性质.
核心素养分析 通过学生的探讨讨论，培养学生的观察力和归纳的能力。通过学生的探讨讨论，培养学生的观察力和归纳的能力。体会求不等式的解与求方程的解的联系与区别，重视数学学习中的类比与转化思想.
学习目标 1、掌握不等式的三个基本性质；2、在不等式的变形中探索求不等式解集的方法.
重点 掌握不等式的三个基本性质..
难点 熟练应用不等式的三条基本性质进行不等式变形.
教学过程
教学环节 教师活动 学生活动 设计意图
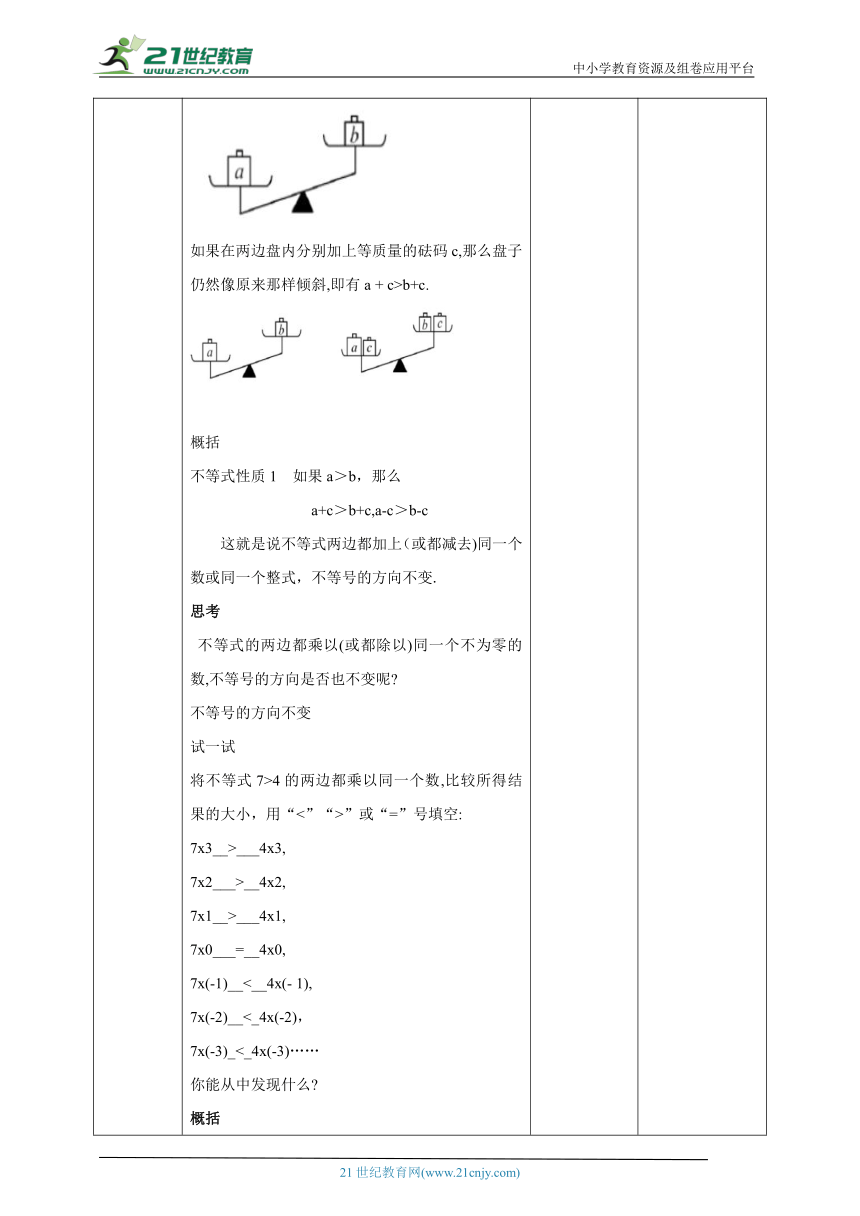
导入新课 一、创设情景，引出课题 什么是等式的基本性质 ？1、等式的两边都加上（或减去）同一个数或同一个整式，所得的结果仍是等式.2、等式的两边都乘以（或除以）同一个数（除数不能为零），所得的结果仍是等式.回顾与探索在解一元一次方程时,我们主要是对方程进行变形.在研究解不等式时,我们先探究不等式的变形规律.如图所示,一个倾斜的天平两边分别放有重物,其质量分别为a和b,a > b. 如果在两边盘内分别加上等质量的砝码c,那么盘子仍然像原来那样倾斜,即有a + c>b+c.概括不等式性质1 如果a＞b，那么 a+c＞b+c,a-c＞b-c这就是说不等式两边都加上（或都减去)同一个数或同一个整式，不等号的方向不变.思考 不等式的两边都乘以(或都除以)同一个不为零的数,不等号的方向是否也不变呢 不等号的方向不变试一试将不等式7>4的两边都乘以同一个数,比较所得结果的大小，用“<”“>”或“=”号填空:7x3__>___4x3,7x2___>__4x2,7x1__>___4x1,7x0___=__4x0,7x(-1)__<__4x(- 1),7x(-2)__<_4x(-2)，7x(-3)_<_4x(-3)……你能从中发现什么 概括不等式的性质2 如果a > b,并且c > 0,那么ac>bc, 不等式的性质3 如果a > b,并且c < 0,那么aca或x通过回忆知识，归纳不等式的基本性质，引入新课，鼓励学生探索新知.
讲授新课 提炼概念利用不等式的性质解不等式的注意事项:1.在运用性质3时,要特别注意：不等式两边都乘以或除以同一个负数时，要改变不等号的方向.2.要注意区分“大于” “不大于”“小于”“不小于”等数学语言的使用，并把这些表示不等关系的语言用数学符号准确地表达出来.3.在数轴上表示解集应注意的问题：方向、空心或实心.典例精讲例1 解不等式:(1) x-7< 8;(2)3x<2x-3.解(1) 不等式的两边都加上7,不等号的方向不变,所以x-7+7<8+7,得x<15.(2)不等式的两边都减去2x(即都加上-2x) ,不等号的方向不变,所以3x-2x<2x-3-2x，得x <-3.这两小题中不等式的变形与方程的什么变形类似 这里的变形，与方程变形中的移项类似.试总结一下:怎样进行不等式的“移项” 在不等式中，移项要变号例2 解不等式:(1) (2) - 2x< 6.解(1)不等式的两边都乘以2,不等号的方向不变,所以 得x>-6.(2)不等式的两边都除以-2(即都乘以),不等号的方向改变,所以得x>-3.这里的变形，与方程变形中的“将未知数的系数化为1”类似,它依据的是不等式的性质2或性质3.要注意：不等式两边都乘以(或都除以)的数是正数还是负数,从而确定变形时不等号的方向是否需要改变.易错点：不等式两边都乘以（或除以）同一个不为0的数时，必须考虑它是正数还是负数，分别根据第2条与第3条性质进行变形，要特别注意不等式的两边都乘以（或都除以）同一个负数时，要改变不等号的方向.（大于号变成小于号，小于号变成大于号）. 培养学生独立思考的习惯，学生讲解自己的思路，其他学生作补充.
要注意区分“大于” “不大于”“小于”“不小于”等数学语言的使用，并把这些表示不等关系的语言用数学符号准确地表达出来.
课堂练习 四、巩固训练 1、若a3，则下列各式正确的是( )A. a+1<4 B. a-3<0 C. a-4>-1 D. a-2<1C3.如果a>b，c<0，那么下列不等式成立的是( )A. a+c>b B. a+c>b-cC. ac-1>bc-1 D. a(c-1)b，得ac2>bc2 B. 由ac2>bc2，得a>bC. 由-2a>2，得a<1 D. 由2x+1>x，得x>1 D5.利用不等式的性质解下列不等式:(1)x-5＞-1;(2)-2x＞3;(3)7x＜6x-6.a是一个整数，你能确定a与3a的大小吗？解：当a＞0时， a＜3a；当a＝0时， a＝ 3a；当a＜0时， a＞3a.
课堂小结 课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)