8.2.2 不等式的简单变形 课件(共29张PPT)
文档属性
| 名称 | 8.2.2 不等式的简单变形 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-30 22:28:13 | ||
图片预览






文档简介
(共29张PPT)
8.2.2 不等式的简单变形
华师大版 七年级 下册
教学目标
教学目标:理解并掌握不等式的三条基本性质.
会用不等式的基本性质,将不等式变形.
教学重点:掌握不等式的三个基本性质.
教学难点:熟练应用不等式的三条基本性质进行不等式变形.
新知导入
情境引入
等式的基本性质:
(1)等式的两边都加上(或都减去)同一个数或同一个整式,等式仍然成立.
(2)等式的两边都乘以(或除以)一个不为0的数,等式仍然成立.
猜想 :不等式也具有同样的性质吗?
新知讲解
合作学习
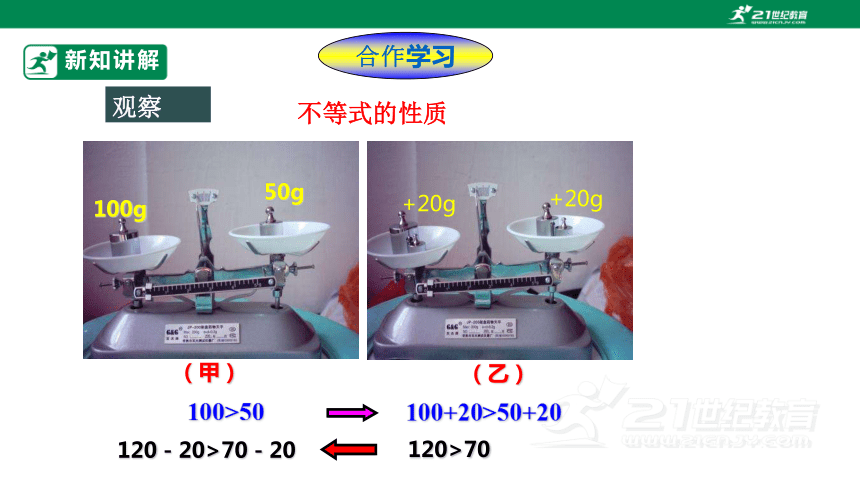
观察
(乙)
100g
50g
120>70
120-20>70-20
+20g
+20g
(甲)
不等式的性质
填一填
如果 7>3,
那么7+5____ 3+5 , 7 -5____3-5
你能总结一下规律吗?
>
>
<
如果-1<3,
那么-1+2____3+2, -1-4____3-4
<
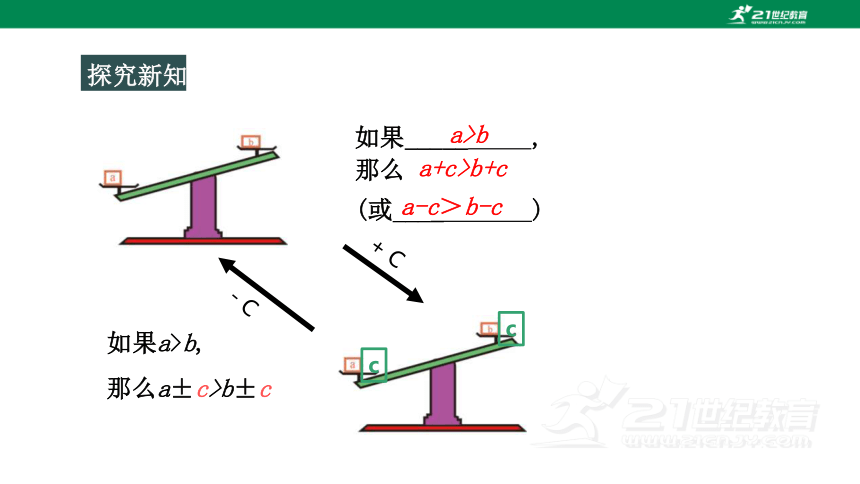
探究新知
+ C
-C
(或____ )
如果_____ ,
那么
如果a>b,
那么a±c>b±c
a>b
a+c>b+c
a-c>b-c
c
c
提炼概念
不等式的两边都加上(或减去)同一个数或同一个整式,
不等号的方向不变.
如果___ _,那么_____ ____.
a>b
a±c>b±c
不等式基本性质1:
用不等号填空:
(1)5 3 ;
5×2 3×2 ;
5÷2 3÷2 .
(2)2 4 ;
2×3 4×3 ;
2÷4 4÷4 .
>
>
>
<
<
<
自己再写一个不等式,分别在它的两边都乘(或除以)同一个正数,
看看有怎样的结果?与同桌互相交流,你们发现了什么规律?
填一填
×3
÷3
(或 )
如果_________,
那么_______
a>b且c>0
ac>bc
如果a > b,c > 0,那么 ac > bc , > .
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式基本性质2:
用不等号填空:
(1)5 3 ;
5×(-2) 3×(-2);
5÷(-2) 3÷(-2) .
(2)2 4 ;
2×(-3) 4×(-3 );
2÷(-4) 4÷(-4) .
>
<
<
<
>
>
自己再写一个不等式,分别在它的两边都乘(或除以)同一个负数,
看看有怎样的结果?与同桌互相交流,你们发现了什么规律?
填一填
如果a > b,c < 0,那么 ac < bc , < .
不等式基本性质3
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
>
不变
>
不变
>
不变
=
变
<
<
<
变
变
变
试一试
将不等式7>4的两边都乘以同一个数,比较所得结果的大小,
用“<” “>”或“=”填空:
这就是说,不等式的两边都乘以(或都除以)同一个正数,
不等号的方向不变;
不等式的两边都乘以(或都除以)同一个负数,
不等号的方向改变.
总结
典例精讲
(1) x -7 < 8,
解:
不等式的两边都加上7,由不等式基本性质1,得
根据不等式基本性质1
即 x < 15 .
例1 解不等式:
(1)x -7 < 8 ;
(2) 3x < 2x -3 .
x -7+7 < 8+7,
(2) 3x < 2x -3,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,
根据不等式基本性质1
即 x < -3.
由(2)可以看出,运用不等式基本性质1 对 3x < 2x-3 进行化简的过程,就是对不等式3x< 2x-3 作了如下变形:
(2) 3x < 2x -3
3x - 2x< -3
这两小题中不等式的变形与方程的什么变形类似?试总结一下:怎样进行不等式的“移项”?
利用不等式的性质 1 可简化为“移项”;利用不等式的性质 2 或性质 3 就是把未知数的系数化为1,要注意乘(或除以)同一个负数时,不等号要改变方向.
例2 解不等式:
(1) (2)-2x<6
归纳概念
利用不等式的性质解不等式的注意事项:
2.要注意区分“大于” “不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来.
3.在数轴上表示解集应注意的问题:方向、空心或实心.
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
课堂练习
1、若aA. a+3C. 6a<6b D. -8a<-8b
D
2.若a>3,则下列各式正确的是( )
A. a+1<4 B. a-3<0 C. a-4>-1 D. a-2<1
C
解:∵a>3 ,
∴ 根据不等式的基本性质1,a-4>3-4
∴a-4>-1,故选C.
3.如果a>b,c<0,那么下列不等式成立的是( )
A. a+c>b B. a+c>b-c
C. ac-1>bc-1 D. a(c-1)D
解:∵c<0,∴c-1<-1,
∵a>b,∴a(c-1)故选D.
4.根据不等式的性质,下列变形正确的是( )
A. 由a>b,得ac2>bc2 B. 由ac2>bc2,得a>b
C. 由-2a>2,得a<1 D. 由2x+1>x,得x>1
B
5.利用不等式的性质解下列不等式:
(2)-2x>3;
(1)x-5>-1;
(3)7x<6x-6.
解:
x>-1+5,
x>4;
即
(1)根据不等式的性质1,两边都加上5,得
(2)根据不等式的性质3,两边都除以-2,得
7x-6x<-6,
x<-6.
即
(3)根据不等式的性质1,两边都减去6x,得
6. a是一个整数,你能确定a与3a的大小吗?
当a>0时, a<3a;
当a=0时, a= 3a;
当a<0时, a>3a.
课堂总结
不等式的简单变形
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
如果a>b,那么a+c>b+c,a-c>b-c
如果a > b,并且c > 0,那么ac>bc,
如果a > b,并且c < 0,那么ac作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
8.2.2 不等式的简单变形
华师大版 七年级 下册
教学目标
教学目标:理解并掌握不等式的三条基本性质.
会用不等式的基本性质,将不等式变形.
教学重点:掌握不等式的三个基本性质.
教学难点:熟练应用不等式的三条基本性质进行不等式变形.
新知导入
情境引入
等式的基本性质:
(1)等式的两边都加上(或都减去)同一个数或同一个整式,等式仍然成立.
(2)等式的两边都乘以(或除以)一个不为0的数,等式仍然成立.
猜想 :不等式也具有同样的性质吗?
新知讲解
合作学习
观察
(乙)
100g
50g
120>70
120-20>70-20
+20g
+20g
(甲)
不等式的性质
填一填
如果 7>3,
那么7+5____ 3+5 , 7 -5____3-5
你能总结一下规律吗?
>
>
<
如果-1<3,
那么-1+2____3+2, -1-4____3-4
<
探究新知
+ C
-C
(或____ )
如果_____ ,
那么
如果a>b,
那么a±c>b±c
a>b
a+c>b+c
a-c>b-c
c
c
提炼概念
不等式的两边都加上(或减去)同一个数或同一个整式,
不等号的方向不变.
如果___ _,那么_____ ____.
a>b
a±c>b±c
不等式基本性质1:
用不等号填空:
(1)5 3 ;
5×2 3×2 ;
5÷2 3÷2 .
(2)2 4 ;
2×3 4×3 ;
2÷4 4÷4 .
>
>
>
<
<
<
自己再写一个不等式,分别在它的两边都乘(或除以)同一个正数,
看看有怎样的结果?与同桌互相交流,你们发现了什么规律?
填一填
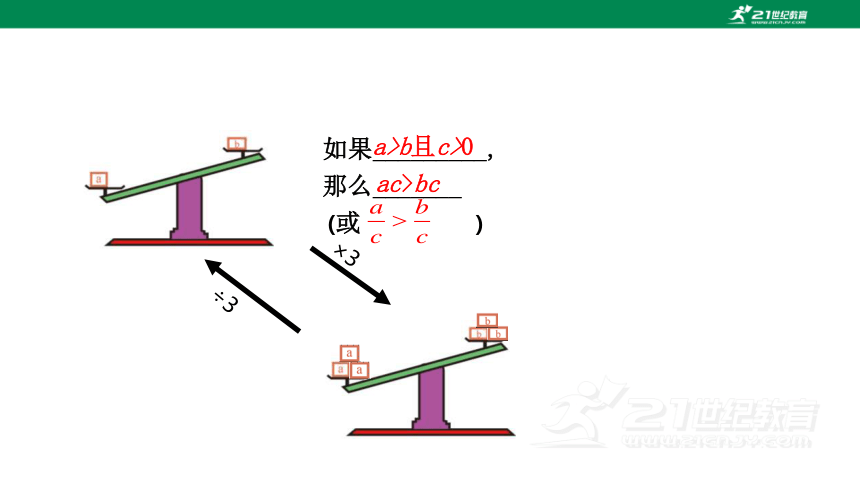
×3
÷3
(或 )
如果_________,
那么_______
a>b且c>0
ac>bc
如果a > b,c > 0,那么 ac > bc , > .
不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式基本性质2:
用不等号填空:
(1)5 3 ;
5×(-2) 3×(-2);
5÷(-2) 3÷(-2) .
(2)2 4 ;
2×(-3) 4×(-3 );
2÷(-4) 4÷(-4) .
>
<
<
<
>
>
自己再写一个不等式,分别在它的两边都乘(或除以)同一个负数,
看看有怎样的结果?与同桌互相交流,你们发现了什么规律?
填一填
如果a > b,c < 0,那么 ac < bc , < .
不等式基本性质3
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
>
不变
>
不变
>
不变
=
变
<
<
<
变
变
变
试一试
将不等式7>4的两边都乘以同一个数,比较所得结果的大小,
用“<” “>”或“=”填空:
这就是说,不等式的两边都乘以(或都除以)同一个正数,
不等号的方向不变;
不等式的两边都乘以(或都除以)同一个负数,
不等号的方向改变.
总结
典例精讲
(1) x -7 < 8,
解:
不等式的两边都加上7,由不等式基本性质1,得
根据不等式基本性质1
即 x < 15 .
例1 解不等式:
(1)x -7 < 8 ;
(2) 3x < 2x -3 .
x -7+7 < 8+7,
(2) 3x < 2x -3,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,
根据不等式基本性质1
即 x < -3.
由(2)可以看出,运用不等式基本性质1 对 3x < 2x-3 进行化简的过程,就是对不等式3x< 2x-3 作了如下变形:
(2) 3x < 2x -3
3x - 2x< -3
这两小题中不等式的变形与方程的什么变形类似?试总结一下:怎样进行不等式的“移项”?
利用不等式的性质 1 可简化为“移项”;利用不等式的性质 2 或性质 3 就是把未知数的系数化为1,要注意乘(或除以)同一个负数时,不等号要改变方向.
例2 解不等式:
(1) (2)-2x<6
归纳概念
利用不等式的性质解不等式的注意事项:
2.要注意区分“大于” “不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来.
3.在数轴上表示解集应注意的问题:方向、空心或实心.
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
课堂练习
1、若a
D
2.若a>3,则下列各式正确的是( )
A. a+1<4 B. a-3<0 C. a-4>-1 D. a-2<1
C
解:∵a>3 ,
∴ 根据不等式的基本性质1,a-4>3-4
∴a-4>-1,故选C.
3.如果a>b,c<0,那么下列不等式成立的是( )
A. a+c>b B. a+c>b-c
C. ac-1>bc-1 D. a(c-1)
解:∵c<0,∴c-1<-1,
∵a>b,∴a(c-1)
4.根据不等式的性质,下列变形正确的是( )
A. 由a>b,得ac2>bc2 B. 由ac2>bc2,得a>b
C. 由-2a>2,得a<1 D. 由2x+1>x,得x>1
B
5.利用不等式的性质解下列不等式:
(2)-2x>3;
(1)x-5>-1;
(3)7x<6x-6.
解:
x>-1+5,
x>4;
即
(1)根据不等式的性质1,两边都加上5,得
(2)根据不等式的性质3,两边都除以-2,得
7x-6x<-6,
x<-6.
即
(3)根据不等式的性质1,两边都减去6x,得
6. a是一个整数,你能确定a与3a的大小吗?
当a>0时, a<3a;
当a=0时, a= 3a;
当a<0时, a>3a.
课堂总结
不等式的简单变形
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
如果a>b,那么a+c>b+c,a-c>b-c
如果a > b,并且c > 0,那么ac>bc,
如果a > b,并且c < 0,那么ac
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
