第17讲+晶体结构的分析与计算(38张ppt)(精讲课件)-2023届高考二轮精准复习45讲(全国通用)
文档属性
| 名称 | 第17讲+晶体结构的分析与计算(38张ppt)(精讲课件)-2023届高考二轮精准复习45讲(全国通用) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2023-01-31 16:38:59 | ||
图片预览







文档简介
(共38张PPT)
高中
化学
二轮精准复习45讲
晶体结构的分析与计算
2023
第17讲
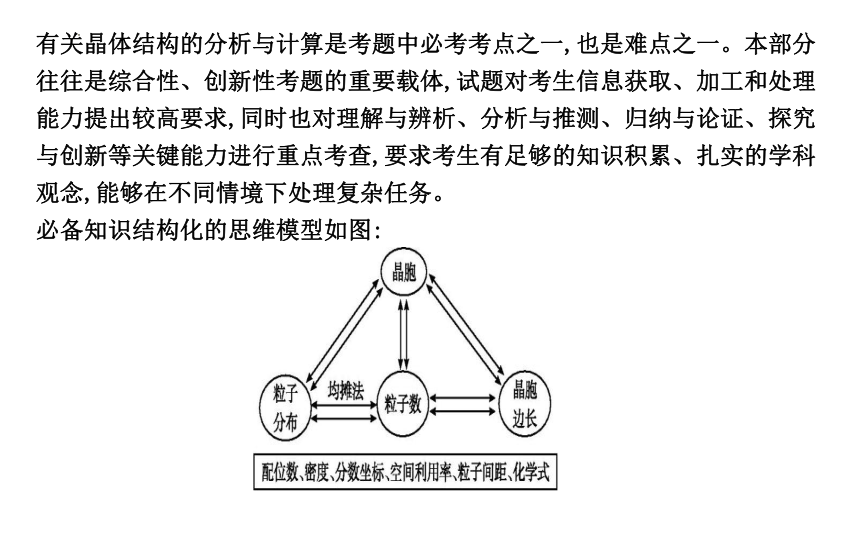
有关晶体结构的分析与计算是考题中必考考点之一,也是难点之一。本部分往往是综合性、创新性考题的重要载体,试题对考生信息获取、加工和处理能力提出较高要求,同时也对理解与辨析、分析与推测、归纳与论证、探究与创新等关键能力进行重点考查,要求考生有足够的知识积累、扎实的学科观念,能够在不同情境下处理复杂任务。
必备知识结构化的思维模型如图:
解答此类问题不仅需要熟练掌握化学中的有关晶体的一些基础知识,而且还要能够准确理解物理、数学中的一些知识点,如推断或计算过程中常会涉及晶体密度、NA、晶体体积、微粒间距离、微粒半径、化学键的夹角、晶胞中的原子坐标等问题,需要我们能够将数理化知识合理地综合应用。其中计算晶胞密度、晶胞粒子间距、晶胞粒子分数坐标是高频考点,预计依然也会是今后考查的主要方向。
题型一 晶体结构的分析方法
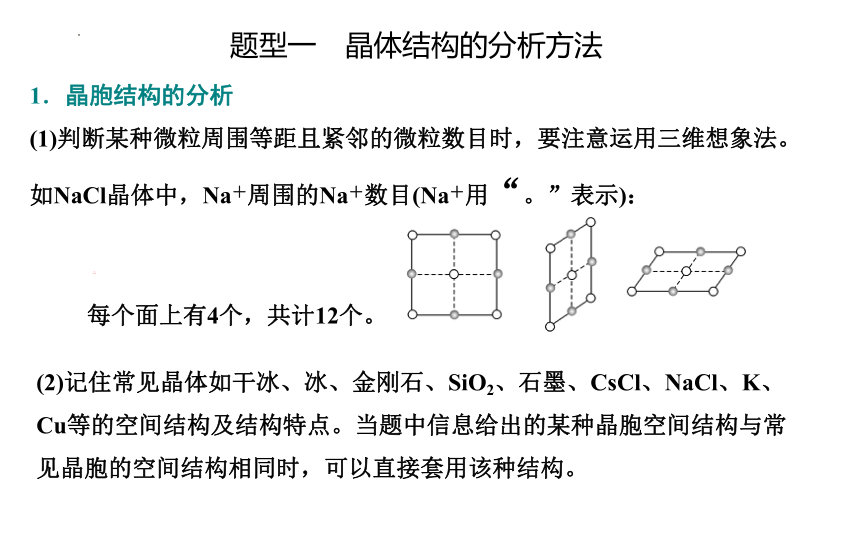
1.晶胞结构的分析
(1)判断某种微粒周围等距且紧邻的微粒数目时,要注意运用三维想象法。如NaCl晶体中,Na+周围的Na+数目(Na+用“。”表示):
每个面上有4个,共计12个。
(2)记住常见晶体如干冰、冰、金刚石、SiO2、石墨、CsCl、NaCl、K、Cu等的空间结构及结构特点。当题中信息给出的某种晶胞空间结构与常见晶胞的空间结构相同时,可以直接套用该种结构。
2.晶胞中微粒数目的计算方法——均摊法
(1)原则:晶胞中任意位置上的一个原子如果是被n个晶胞所共有,那么,每个晶胞对这个原子分得的份额就是1/n。
(2)方法
长方体(包括立方体)晶胞中不同位置的微粒数的计算方法如图所示:
角度一 确定晶胞中粒子分数坐标
题型二 晶胞参数及相关计算
解题策略
考向二 六方晶胞的原子坐标
2.金属镁晶体为六方最密堆积,晶胞可用如图表示。设晶胞中A
点原子坐标为(0,0,0),则B点原子坐标为 。
解析:可先画出六方晶胞沿z轴的投影图,过体心原子的投影点B1画出与x、y轴的平行线,可得x、y轴坐标的数值,此处求原子坐标用的是斜坐标系,矢量确定依据“平行四边形法则”。如图:
练后归纳
在晶体学习中要避免套路固定、死板,从不同角度认识晶胞,比如尝试画晶胞投影图,并且利用投影图去推导原子坐标及其之间的距离,即晶胞除了有三维结构,还可降维到二维或一维或整体平移等,更准确的从微观上认识晶胞的微观结构,进而化繁为简顺利解决问题。
角度二 晶胞中微粒间的距离、原子半径的计算
[典例2] (2019·全国Ⅰ卷节选)图(a)是MgCu2的拉维斯结构,Mg以金刚石方式堆积,八面体空隙和半数的四面体空隙中,填入以四面体方式排列的Cu。图(b)是沿立方格子对角面取得的截图。可见,Cu原子之间最短距离x=
pm,Mg原子之间最短距离y= pm。
规律方法
计算晶胞中微粒间距离的常用关系式
有关晶胞中微粒间距离、微粒半径的计算通常是计算体心立方堆积和面心立方最密堆积两种模型中微粒间的距离,计算中常常需要使用数学中立体几何的知识,以金属晶体为例,常用到如下几组公式(设棱长为a,原子半径为r):
考向一 晶胞中微粒间的距离
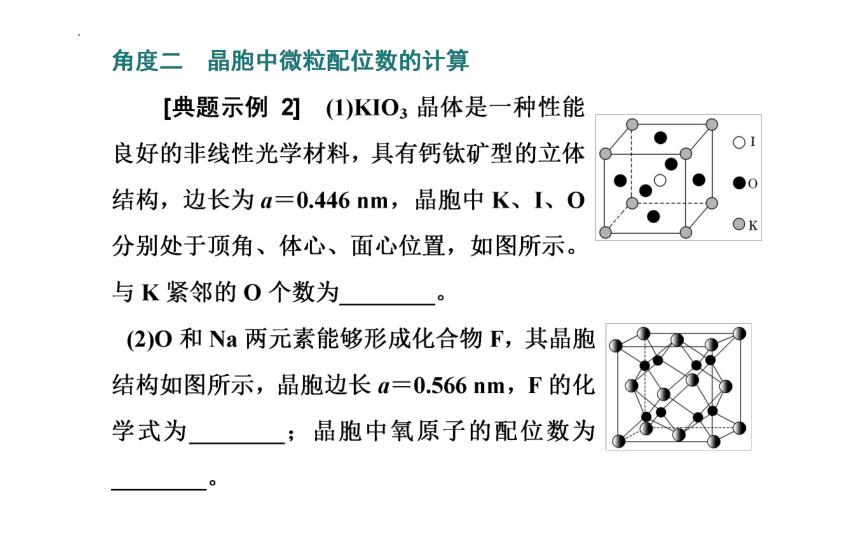
1.(2017·全国Ⅰ卷节选)KIO3晶体是一种性能良好的非线性光学材料,具有钙钛矿型的立体结构,边长为a=0.446 nm,晶胞中K、I、O分别处于顶角、体心、面心位置,如图所示。K与O间的最短距离为 nm,与K紧邻的O个数为 。
答案:0.315 12
思维建模
晶胞中微粒间距离的计算思维模版
考向二 晶胞中微粒半径的计算
2.(2017·全国Ⅲ卷节选)MgO具有NaCl型结构(如图),其中阴离子采用面心立方最密堆积方式,X射线衍射实验测得MgO的晶胞参数为a=0.420 nm,则r(O 2-)为 nm。MnO也属于NaCl型结构,晶胞参数为a′=0.448 nm,则r(Mn2+)为 nm。
答案:0.148 0.076
角度三 晶胞边长与M、ρ、NA等的计算
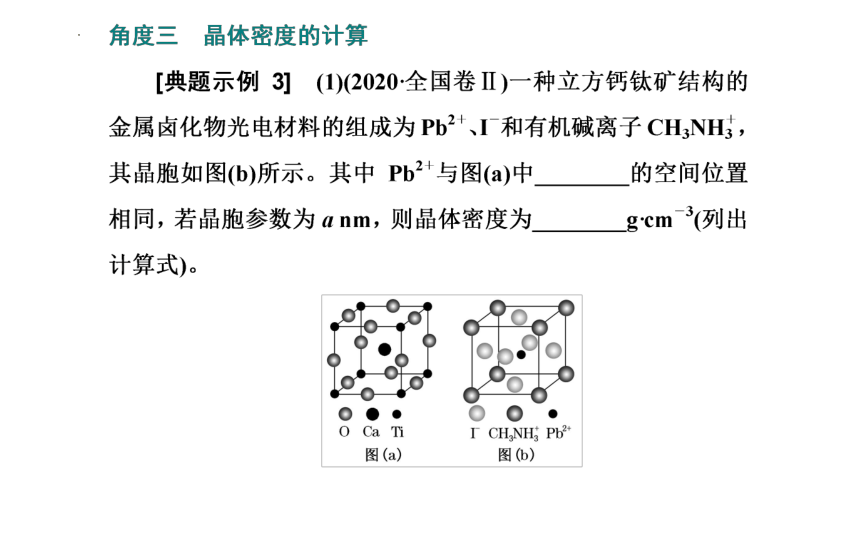
[典例3] (2019·全国Ⅱ卷节选)一种四方结构的超导化合物的晶胞如图1所示。晶胞中Sm和As原子的投影位置如图2所示。
图中F-和O2-共同占据晶胞的上下底面位置,若两者的比例依次用x和1-x代表,则该化合物的化学式表示为 ;通过测定密度ρ和晶胞参数,可以计算该物质的x值,完成它们关系表达式:ρ=
g·cm-3。
解题策略
若1个晶胞中含有x个微粒,则1 mol晶胞中含有x mol微粒,其质量为xM g(M为微粒的相对“分子”质量);1个晶胞的质量为ρa3 g(a3为晶胞的体积,ρ为晶胞的密度),则1 mol晶胞的质量为ρa3NA g,因此有xM=ρa3NA。则解决此类问题的一般策略为:
第一步:确定各原子在晶胞中的个数和晶体的化学式。
第二步:表示、计算每个晶胞的质量。
第三步:明确晶胞边长,计算一个晶胞的体积。
第四步:代入密度公式。
(2)(2019·全国Ⅰ卷)图(a)是MgCu2的拉维斯结构,Mg以金刚石方式堆积,八面体空隙和半数的四面体空隙中,填入以四面体方式排列的Cu。图(b)是沿立方格子对角面取得的截图。设阿伏加德罗常数的值为NA,则MgCu2的密度是 g·cm-3(列出计算表达式)。
(3) (2021·广东新高考适应性考试)贵金属磷化物Rh2P(化学式量为237)可用作电解水的高效催化剂,其立方晶胞如图所示。已知晶胞参数为a nm,晶体中与P距离最近的Rh的数目为 ,晶体的密度为 g·cm-3
(列出计算式)。
(2)(2017·全国Ⅱ卷)我国科学家最近成功合成了世界上首个五氮阴离子盐(N5)6(H3O)3(NH4)4Cl(用R代表)。R的晶体密度为d g·cm-3,其立方晶胞参数为a nm,晶胞中含有y个[(N5)6(H3O)3(NH4)4Cl]单元,该单元的相对质量为M,则y的计算表达式为 。
(3)(2020·山东淄博一模)某钙钛矿太阳能电池材料的晶胞如图所示,其晶胞参数为d pm、密度为ρ g·cm-3。则该晶体的摩尔质量为 g·mol-1。(用含d、ρ等符号的式子表示,用NA表示阿伏加德罗常数的值)
答案:(3)d3ρNA×10-30
高中
化学
二轮精准复习45讲
晶体结构的分析与计算
2023
第17讲
有关晶体结构的分析与计算是考题中必考考点之一,也是难点之一。本部分往往是综合性、创新性考题的重要载体,试题对考生信息获取、加工和处理能力提出较高要求,同时也对理解与辨析、分析与推测、归纳与论证、探究与创新等关键能力进行重点考查,要求考生有足够的知识积累、扎实的学科观念,能够在不同情境下处理复杂任务。
必备知识结构化的思维模型如图:
解答此类问题不仅需要熟练掌握化学中的有关晶体的一些基础知识,而且还要能够准确理解物理、数学中的一些知识点,如推断或计算过程中常会涉及晶体密度、NA、晶体体积、微粒间距离、微粒半径、化学键的夹角、晶胞中的原子坐标等问题,需要我们能够将数理化知识合理地综合应用。其中计算晶胞密度、晶胞粒子间距、晶胞粒子分数坐标是高频考点,预计依然也会是今后考查的主要方向。
题型一 晶体结构的分析方法
1.晶胞结构的分析
(1)判断某种微粒周围等距且紧邻的微粒数目时,要注意运用三维想象法。如NaCl晶体中,Na+周围的Na+数目(Na+用“。”表示):
每个面上有4个,共计12个。
(2)记住常见晶体如干冰、冰、金刚石、SiO2、石墨、CsCl、NaCl、K、Cu等的空间结构及结构特点。当题中信息给出的某种晶胞空间结构与常见晶胞的空间结构相同时,可以直接套用该种结构。
2.晶胞中微粒数目的计算方法——均摊法
(1)原则:晶胞中任意位置上的一个原子如果是被n个晶胞所共有,那么,每个晶胞对这个原子分得的份额就是1/n。
(2)方法
长方体(包括立方体)晶胞中不同位置的微粒数的计算方法如图所示:
角度一 确定晶胞中粒子分数坐标
题型二 晶胞参数及相关计算
解题策略
考向二 六方晶胞的原子坐标
2.金属镁晶体为六方最密堆积,晶胞可用如图表示。设晶胞中A
点原子坐标为(0,0,0),则B点原子坐标为 。
解析:可先画出六方晶胞沿z轴的投影图,过体心原子的投影点B1画出与x、y轴的平行线,可得x、y轴坐标的数值,此处求原子坐标用的是斜坐标系,矢量确定依据“平行四边形法则”。如图:
练后归纳
在晶体学习中要避免套路固定、死板,从不同角度认识晶胞,比如尝试画晶胞投影图,并且利用投影图去推导原子坐标及其之间的距离,即晶胞除了有三维结构,还可降维到二维或一维或整体平移等,更准确的从微观上认识晶胞的微观结构,进而化繁为简顺利解决问题。
角度二 晶胞中微粒间的距离、原子半径的计算
[典例2] (2019·全国Ⅰ卷节选)图(a)是MgCu2的拉维斯结构,Mg以金刚石方式堆积,八面体空隙和半数的四面体空隙中,填入以四面体方式排列的Cu。图(b)是沿立方格子对角面取得的截图。可见,Cu原子之间最短距离x=
pm,Mg原子之间最短距离y= pm。
规律方法
计算晶胞中微粒间距离的常用关系式
有关晶胞中微粒间距离、微粒半径的计算通常是计算体心立方堆积和面心立方最密堆积两种模型中微粒间的距离,计算中常常需要使用数学中立体几何的知识,以金属晶体为例,常用到如下几组公式(设棱长为a,原子半径为r):
考向一 晶胞中微粒间的距离
1.(2017·全国Ⅰ卷节选)KIO3晶体是一种性能良好的非线性光学材料,具有钙钛矿型的立体结构,边长为a=0.446 nm,晶胞中K、I、O分别处于顶角、体心、面心位置,如图所示。K与O间的最短距离为 nm,与K紧邻的O个数为 。
答案:0.315 12
思维建模
晶胞中微粒间距离的计算思维模版
考向二 晶胞中微粒半径的计算
2.(2017·全国Ⅲ卷节选)MgO具有NaCl型结构(如图),其中阴离子采用面心立方最密堆积方式,X射线衍射实验测得MgO的晶胞参数为a=0.420 nm,则r(O 2-)为 nm。MnO也属于NaCl型结构,晶胞参数为a′=0.448 nm,则r(Mn2+)为 nm。
答案:0.148 0.076
角度三 晶胞边长与M、ρ、NA等的计算
[典例3] (2019·全国Ⅱ卷节选)一种四方结构的超导化合物的晶胞如图1所示。晶胞中Sm和As原子的投影位置如图2所示。
图中F-和O2-共同占据晶胞的上下底面位置,若两者的比例依次用x和1-x代表,则该化合物的化学式表示为 ;通过测定密度ρ和晶胞参数,可以计算该物质的x值,完成它们关系表达式:ρ=
g·cm-3。
解题策略
若1个晶胞中含有x个微粒,则1 mol晶胞中含有x mol微粒,其质量为xM g(M为微粒的相对“分子”质量);1个晶胞的质量为ρa3 g(a3为晶胞的体积,ρ为晶胞的密度),则1 mol晶胞的质量为ρa3NA g,因此有xM=ρa3NA。则解决此类问题的一般策略为:
第一步:确定各原子在晶胞中的个数和晶体的化学式。
第二步:表示、计算每个晶胞的质量。
第三步:明确晶胞边长,计算一个晶胞的体积。
第四步:代入密度公式。
(2)(2019·全国Ⅰ卷)图(a)是MgCu2的拉维斯结构,Mg以金刚石方式堆积,八面体空隙和半数的四面体空隙中,填入以四面体方式排列的Cu。图(b)是沿立方格子对角面取得的截图。设阿伏加德罗常数的值为NA,则MgCu2的密度是 g·cm-3(列出计算表达式)。
(3) (2021·广东新高考适应性考试)贵金属磷化物Rh2P(化学式量为237)可用作电解水的高效催化剂,其立方晶胞如图所示。已知晶胞参数为a nm,晶体中与P距离最近的Rh的数目为 ,晶体的密度为 g·cm-3
(列出计算式)。
(2)(2017·全国Ⅱ卷)我国科学家最近成功合成了世界上首个五氮阴离子盐(N5)6(H3O)3(NH4)4Cl(用R代表)。R的晶体密度为d g·cm-3,其立方晶胞参数为a nm,晶胞中含有y个[(N5)6(H3O)3(NH4)4Cl]单元,该单元的相对质量为M,则y的计算表达式为 。
(3)(2020·山东淄博一模)某钙钛矿太阳能电池材料的晶胞如图所示,其晶胞参数为d pm、密度为ρ g·cm-3。则该晶体的摩尔质量为 g·mol-1。(用含d、ρ等符号的式子表示,用NA表示阿伏加德罗常数的值)
答案:(3)d3ρNA×10-30
同课章节目录
