第六章 计数原理 章末综合测试-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册(含解析)
文档属性
| 名称 | 第六章 计数原理 章末综合测试-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 222.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 05:04:11 | ||
图片预览




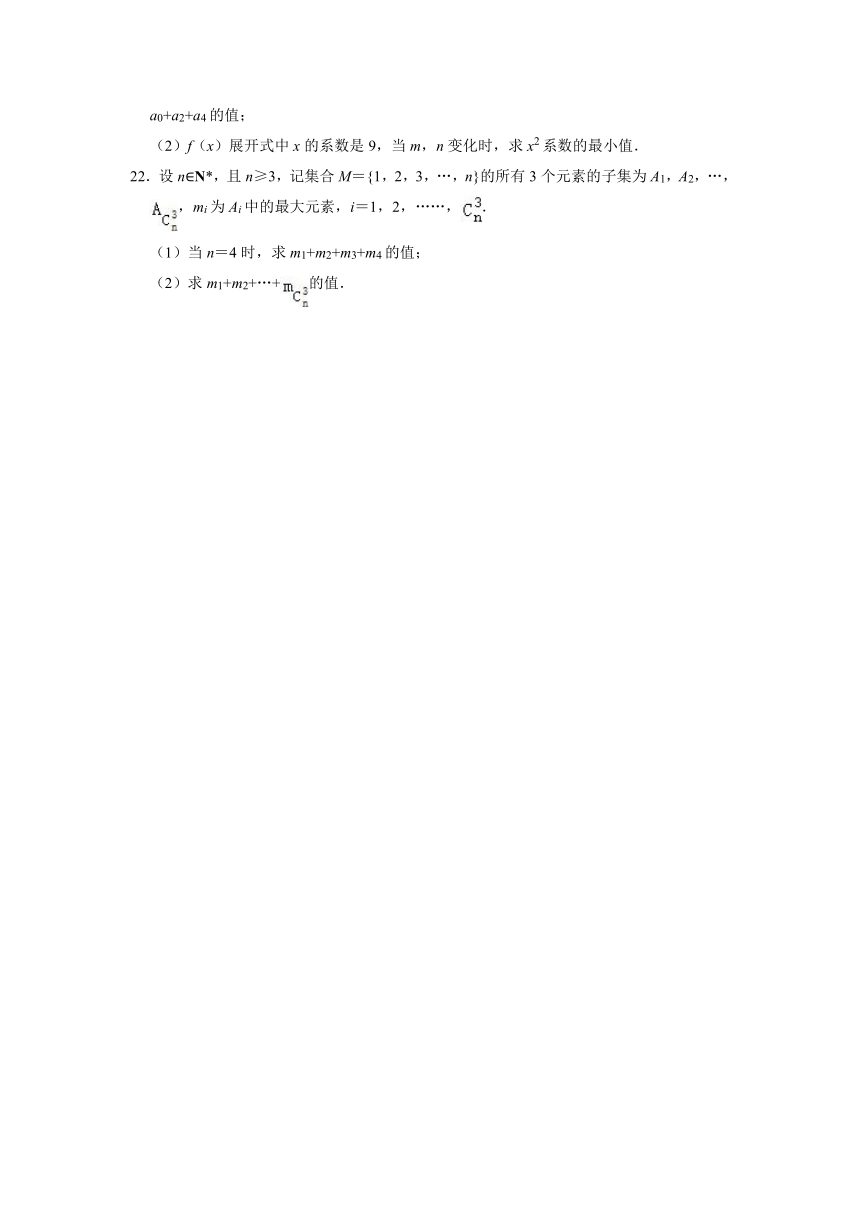
文档简介
绝密★启用前
第六章 计数原理 章末综合测试
选择性必修第三册高中数学人教A版(2019)
考试范围:选择性必修第三册第六章 计数原理 ;考试满分:150分
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.的二项展开式中的常数项是( )
A.﹣20 B.﹣15 C.15 D.20
2.为培养学生的兴趣爱好,丰富学生的课余生活,某校团委开设了70个社团供学生自由选择.现已知甲、乙两位同学均准备从“创客空间”、“春柳文学社”、“舞龙协会”这三个社团中选择一个报名,则这两位同学的不同报名方案种数为( )
A.6 B.8 C.9 D.12
3.今天是星期五,经过7天后还是星期五,那么经过8100天后是( )
A.星期三 B.星期四 C.星期五 D.星期六
4.在(1﹣x)(2﹣x)(3﹣x)(4﹣x)(5﹣x)的展开式中,x4的系数为( )
A.15 B.﹣15 C.11 D.﹣11
5.已知电影院有三部影片同时上映,一部动画片,一部喜剧片,一部动作片,5名同学前去观看,若喜剧片和动作片各至少两人观看,则不同的观影方案共有( )种.
A.30 B.40 C.50 D.80
6.设n∈N*,xn=a0+a1(x﹣1)+ +an(x﹣1)n=b0+b1(x﹣2)+ +bn(x﹣2)n,则( )
A.b0﹣a0+b1﹣a1+ +bn﹣an=3n﹣2n
B.=2(a0+a1+ +an)
C.a0+a1+ +an=(a0+a1+ +an)
D.b1+4b2+ +n2bn=(a0+a1+ +an)
7.若(1﹣ax+x2)(1﹣x)8的展开式中含x2的项的系数为21,则a=( )
A.﹣3 B.﹣2 C.﹣1 D.1
8.为了进一步提高广大市民的生态文明建设意识,某市规定每年4月25日为“创建文明城 生态志愿行”为主题的生态活动日.现有5名同学参加志愿活动,需要携带勾子、铁锹、夹子三种劳动工具,要求每人都要携带一个工具,并且要求:带一个勾子,铁锹至少带2把,夹子至少带一个,则不同的安排方案共有( )
A.50种 B.60种 C.70种 D.80种
第Ⅱ卷
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.用0、1、2、3、4这五个数字组成无重复数字的自然数,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301、423等都是“凹数”,则下列结论中正确的是( )
A.组成的三位数的个数为60
B.在组成的三位数中,偶数的个数为30
C.在组成的三位数中,“凹数”的个数为20
D.在组成的三位数中,“凹数”的个数为24
10.若(x∈R),则下列判断正确的有( )
A.a0=1
B.
C.
D.
11.下列结论正确的是( )
A.
B.若,则
C.
D.
12.甲、乙、丙、丁、戊共5位志愿者被安排到A,B,C,D四所山区学校参加支教活动,要求每所学校至少安排一位志愿者,且每位志愿者只能到一所学校支教,则下列结论正确的是( )
A.不同的安排方法共有240种
B.甲志愿者被安排到A学校的概率是
C.若A学校安排两名志愿者,则不同的安排方法共有120种
D.在甲志愿者被安排到A学校支教的前提下,A学校有两名志愿者的概率是
三、填空题:本题共4小题,每小题5分,共20分。
13.2022年北京冬奥会期间,为了保障运动员健康,需要从北京某医院运动损伤科的5名男医生(含1名主任医师)、3名女医生(含1名主任医师)中分别选派3名男医生和2名女医生,要求至少有一名主任医师参加,则不同的选派方案共有 种.(用数字作答)
14.(a+)3+(a﹣)4的展开式中的系数为 (用数字作答).
15.某大学一寝室4人参加疫情防控讲座,4人就坐在一排有13个空位的座位上,根据防疫要求,任意两人之间需间隔1米以上(两个空位),则不同的就坐方法有 种.
16.已知,则a1+a2+a3+ +a2020的值为 ;a1+2a2+3a3+ +2020a2020的值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(1)解不等式.
(2)若,求正整数n.
18.“渐升数”是指除最高数位上的数字外,其余每一个数字均比其左边的数字大的正整数(如13456和35678都是五位“渐升数”).
(1)求五位“渐升数”的个数;
(2)如果把所有的五位“渐升数”按照从小到大的顺序排列,求第120个五位“渐升数”.
19.从7名男生5名女生中选取5人,分别求符合下列条件的选法有多少种?
(1)其中的A,B必须当选;
(2)A,B恰有一人当选;
(3)选取3名男生和2名女生分别担任班长、体育委员等5种不同职务,但体育委员必须由男生担任,班长必须由女生担任.
20.按照下列要求,分别求有多少种不同的方法?(列式并用数字作答)
(1)5个不同的小球放入4个不同的盒子,每个盒子至少放一个小球;
(2)6个不同的小球放入4个不同的盒子,每个盒子至少一个小球;
(3)6个相同的小球放入4个不同的盒子,每个盒子至少一个小球
(4)6个不同的小球放入4个不同的盒子,恰有1个空盒.
21.设m,n∈N,f(x)=(1+x)m+(1+x)n.
(1)当m=n=5时,若,求a0+a2+a4的值;
(2)f(x)展开式中x的系数是9,当m,n变化时,求x2系数的最小值.
22.设n∈N*,且n≥3,记集合M={1,2,3,…,n}的所有3个元素的子集为A1,A2,…,,mi为Ai中的最大元素,i=1,2,……,.
(1)当n=4时,求m1+m2+m3+m4的值;
(2)求m1+m2+…+的值.
第六章 计数原理 章末综合测试
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.的二项展开式中的常数项是( )
A.﹣20 B.﹣15 C.15 D.20
解:展开式第r+1项:
,
3﹣=0,可得r=2时,
的二项展开式中的常数项是,
故选:C.
2.为培养学生的兴趣爱好,丰富学生的课余生活,某校团委开设了70个社团供学生自由选择.现已知甲、乙两位同学均准备从“创客空间”、“春柳文学社”、“舞龙协会”这三个社团中选择一个报名,则这两位同学的不同报名方案种数为( )
A.6 B.8 C.9 D.12
解:不妨记“创客空间”、“春柳文学社”、“舞龙协会”分别为a、b、c,
则这两位同学的报名方案有aa,ab,ac,ba,bb,bc,ca,cb,cc,共9种.
故选:C.
3.今天是星期五,经过7天后还是星期五,那么经过8100天后是( )
A.星期三 B.星期四 C.星期五 D.星期六
解:8100=(7+1)100=7100+C799+C798+...+C7+1,
因为7100+C799+C798+...+C7能被7整除,所以8100除以7的余数为1,
故经过8100天后是星期六.
故选:D.
4.在(1﹣x)(2﹣x)(3﹣x)(4﹣x)(5﹣x)的展开式中,x4的系数为( )
A.15 B.﹣15 C.11 D.﹣11
解:展开式中含x4的项为:
在1﹣x,2﹣x,3﹣x,4﹣x,5﹣x这5个代数式中4个取﹣x,其余1个代数式取常数,
∴展开式中x4的系数为1+2+3+4+5=15,
故选:A.
5.已知电影院有三部影片同时上映,一部动画片,一部喜剧片,一部动作片,5名同学前去观看,若喜剧片和动作片各至少两人观看,则不同的观影方案共有( )种.
A.30 B.40 C.50 D.80
解:由题可知共有三类:①2人看喜剧片,2人看动作片,1人看动画片,方案数为:=30;
②3人看喜剧片,2人看动作片,0人看动画片,方案数为:=10;
③2人看喜剧片,3人看动作片,0人看动画片,方案数为:=10,
共有30+10+10=50种方案.
故选:C.
6.设n∈N*,xn=a0+a1(x﹣1)+ +an(x﹣1)n=b0+b1(x﹣2)+ +bn(x﹣2)n,则( )
A.b0﹣a0+b1﹣a1+ +bn﹣an=3n﹣2n
B.=2(a0+a1+ +an)
C.a0+a1+ +an=(a0+a1+ +an)
D.b1+4b2+ +n2bn=(a0+a1+ +an)
解:由二项式定理知:
xn=[(x﹣1)+1]n=C+C(x﹣1)+C(x﹣1)2+ +C(x﹣1)n,
∴ai=C(i=0,1,2...n),令x=2,则有a0+a1+ +an=2n;
xn=[(x﹣2)+2]n=C 2n+C 2n﹣1 (x﹣2)+C 2n﹣2 (x﹣2)2+ +C(x﹣2)n,
∴bi=C2n﹣i (i=0,1,2,...,n),令x=3,则有b0+b1+ +bn=3n;
故有b0﹣a0+b1﹣a1+ +bn﹣an=3n﹣2n,A正确;
令n=2,则有a0=1,a1=2,a2=1,b0=4,b1=4,b2=1,
分别代入B,C,D选项:
=4+2+1=7,2(a0+a1+a2)=8,B错误;
a0+a1+a2=1+1+=,(a0+a1+a2)=,C错误;
b1+4b2=4+4=8,(a0+a1+a2)=6,D错误;
故选:A.
7.若(1﹣ax+x2)(1﹣x)8的展开式中含x2的项的系数为21,则a=( )
A.﹣3 B.﹣2 C.﹣1 D.1
解:分三种情况:
(1)当因式(1﹣ax+x2)中取1时,含x2的项为,其系数为28;
(2)当因式(1﹣ax+x2)中取﹣ax时,含x2的项为(﹣ax) ,其系数为8a;
(3)当因式(1﹣ax+x2)中取x2时,含x2的项为x2 ,其系数为1,
所以展开式中含x2的项的系数为28+8a+1=21,解得a=﹣1.
故选:C.
8.为了进一步提高广大市民的生态文明建设意识,某市规定每年4月25日为“创建文明城 生态志愿行”为主题的生态活动日.现有5名同学参加志愿活动,需要携带勾子、铁锹、夹子三种劳动工具,要求每人都要携带一个工具,并且要求:带一个勾子,铁锹至少带2把,夹子至少带一个,则不同的安排方案共有( )
A.50种 B.60种 C.70种 D.80种
解:携带工具方案有两类:
第一类,1个勾子,1个夹子,3把铁锹,所以携带工具的方案数有=20种;
第二类,1个勾子,2个夹子,2把铁锹,所以携带工具的方案数有CC=30种;
所以不同的安排方案共有20+30=50种.
故选:A.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.用0、1、2、3、4这五个数字组成无重复数字的自然数,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301、423等都是“凹数”,则下列结论中正确的是( )
A.组成的三位数的个数为60
B.在组成的三位数中,偶数的个数为30
C.在组成的三位数中,“凹数”的个数为20
D.在组成的三位数中,“凹数”的个数为24
解:用0、1、2、3、4这五个数字组成无重复数字的自然数,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,
对于A,因为百位数上的数字不能为零,所以组成的三位数的个数为,故A不正确;
对于B,将三位数的偶数分为两类,①个位数为0,则有种,②个位数为2或4,则有=2×3×3=18种,
所以在组成的三位数中,偶数的个数为12+18=30,故B正确;
对于C、D,将这些“凹数”分为三类,①十位为0,则有种,
②十位为1,则有种,
③十位为2,则有种,
所以在组成的三位数中,“凹数”的个数为12+6+2=20,故C正确,D不正确.
故选:BC.
10.若(x∈R),则下列判断正确的有( )
A.a0=1
B.
C.
D.
解:由题意,当x=0时,a0=12009=1,
当x=1时,a0+a1+a2+a3+…+a2009=( 1)2009= 1,
当x=﹣1时,a0﹣a1+a2﹣a3+…﹣a2009=32009,
所以,a0+a2+a4+…+a2008=,
,
故选:ACD.
11.下列结论正确的是( )
A.
B.若,则
C.
D.
解:对于A,=(1+2)50=350,故A正确;
对于B,若,
则令x=﹣1,可得a0﹣a1+a2﹣a3+…+a50=,故B正确;
对于C,因为m===n,即m=n,
所以+3+5+ +101=+++ ++2+4+ +100
=250+2(+2+ +50)=250+2(50+50+…+50)
=250+2×50×249=51×250,故C错误;
对于D,因为m=n,所以
=50(++…+),
而++…+=++…++=×249,
所以=50××249=25×249,故D正确.
故选:ABD.
12.甲、乙、丙、丁、戊共5位志愿者被安排到A,B,C,D四所山区学校参加支教活动,要求每所学校至少安排一位志愿者,且每位志愿者只能到一所学校支教,则下列结论正确的是( )
A.不同的安排方法共有240种
B.甲志愿者被安排到A学校的概率是
C.若A学校安排两名志愿者,则不同的安排方法共有120种
D.在甲志愿者被安排到A学校支教的前提下,A学校有两名志愿者的概率是
解:甲、乙、丙、丁、戊共5位志愿者被安排到A,B,C,D四所山区学校参加支教活动,
则共有种安排方法,故A正确;
甲志愿者被安排到A学校,
若A学校只有一个人,则有种安排方法,
若A学校只有2个人,则有种安排方法,
所以甲志愿者被安排到A学校有36+24=60种安排方法,
所以甲志愿者被安排到A学校的概率是,故B正确;
若A学校安排两名志愿者,则不同的安排方法共有种,故C错误;
甲志愿者被安排到A学校有60种安排方法,
在甲志愿者被安排到A学校支教的前提下,A学校有两名志愿者的安排方法有24种,
所以在甲志愿者被安排到A学校支教的前提下,A学校有两名志愿者的概率是,故D正确.
故选:ABD.
三、填空题:本题共4小题,每小题5分,共20分。
13.2022年北京冬奥会期间,为了保障运动员健康,需要从北京某医院运动损伤科的5名男医生(含1名主任医师)、3名女医生(含1名主任医师)中分别选派3名男医生和2名女医生,要求至少有一名主任医师参加,则不同的选派方案共有 26 种.(用数字作答)
解:根据题意,从5名男医生(含一名主任医师)、3名女医生(含一名主任医师)中分别选派3名男医生和2名女医生,
共有CC=10×3=30种选派方案,
如果所选的男女主任都没有参加,共有C×C=4种选派方案,
所以至少有一名主任医师参加有30﹣4=26种,
故答案为:26.
14.(a+)3+(a﹣)4的展开式中的系数为 9 (用数字作答).
解:对于,根据二项展开式:,
当r=1时,系数为;
对于,根据二项展开式:,
当r=2时,系数为;
故(a+)3+(a﹣)4的展开式中的系数为3+6=9.
故答案为:9.
15.某大学一寝室4人参加疫情防控讲座,4人就坐在一排有13个空位的座位上,根据防疫要求,任意两人之间需间隔1米以上(两个空位),则不同的就坐方法有 840 种.
解:先假设每人坐一个位置相当于去掉4个位置,再将4人中间任意两人之间放进2个空位,
此时空位一共还剩3个,若将这三个连在一起插入4人之间和两侧的空位上,有5种放法;
若将这三个分成两组,一组两个,一组一个,插入4人之间和两侧的空位上,有种放法;
若将这三个分成三组插入4人之间和两侧的空位上,有种放法,
故不同的就坐方法为种.
故答案为:840.
16.已知,则a1+a2+a3+ +a2020的值为 ﹣1 ;a1+2a2+3a3+ +2020a2020的值为 0 .
解:令x=0,则a0=1,
令x=1,则a0+a1+a2+a3+ +a2020=0,
∴a1+a2+a3+ +a2020=﹣1,
∵,
∴f′(x)=﹣2020(1﹣x)1999=a1+2a2x+3a3x2+ +2020a2020x1999,
令x=1,则a1+2a2+3a3+ +2020a2020=0,
故答案为:﹣1;0.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(1)解不等式.
(2)若,求正整数n.
解:(1),
则,
则(10﹣x)(9﹣x)<6,
即7<x<12,
又,
即x=8,
即不等式的解集为{8};
(2)已知,
则,
即n(n﹣1)(n﹣2)=364×6=14×13×12,
即n=14.
18. “渐升数”是指除最高数位上的数字外,其余每一个数字均比其左边的数字大的正整数(如13456和35678都是五位“渐升数”).
(1)求五位“渐升数”的个数;
(2)如果把所有的五位“渐升数”按照从小到大的顺序排列,求第120个五位“渐升数”.
解:(1)根据题意,五位“渐升数”要求除万位数字之外,每一个数字均比其左边的数字大,
故要求的五位“渐升数”中不能有0.
只需在其他9个数字中任取5个,将其从小到大排列,即可得一个五位“渐升数”,故每种取法对应1个“渐升数”,
则五位“渐升数”共有个
(2)对于所有的五位“渐升数”,1在最高数位的有个,
2在最高数位的有个,
3在最高数位的有个,
因为70+35+15=120,
所以第120个“渐升数”是最高数位为3的最大的五位“渐升数”,为36789.
19.从7名男生5名女生中选取5人,分别求符合下列条件的选法有多少种?
(1)其中的A,B必须当选;
(2)A,B恰有一人当选;
(3)选取3名男生和2名女生分别担任班长、体育委员等5种不同职务,但体育委员必须由男生担任,班长必须由女生担任.
解:(1)根据题意,先选出A,B,再从剩下的10人中选3人,
共有种选法;
(2)根据题意,先在AB中选出1人,再从剩下的10人中选4人,
共有种选法;
(3)根据题意,选出一名男生担任体育委员共有种情况,
选出一名女生担任班长共有种情况.
剩下6名男生再选2人,4名女生再选1人,担任其它3个班委,共有种情况,
所以共有种选法.
20.按照下列要求,分别求有多少种不同的方法?(列式并用数字作答)
(1)5个不同的小球放入4个不同的盒子,每个盒子至少放一个小球;
(2)6个不同的小球放入4个不同的盒子,每个盒子至少一个小球;
(3)6个相同的小球放入4个不同的盒子,每个盒子至少一个小球
(4)6个不同的小球放入4个不同的盒子,恰有1个空盒.
解:(1)根据题意,先将5个小球分为4组,再将4组放入4个盒子即可,
有种放法;
(2)根据题意,先将6个小球分为4组,有+C种分组方法,
再将4组放入4个盒子,有A种放法,
则有(+C)×A=1560种放法;
(3)根据题意,由于小球相同,将6个小球分为4组,依次放入4个盒子即可,
利用挡板法分析:将6个小球排成一排,中间有5个空位,
在其中任选3个空位,插入挡板,可以将6个小球分为4组,
进而依次放入4个盒子,有C=10种放法;
(4)根据题意,先将6个小球分为3组,有CCC++C种分组方法,
再从4个盒子中任选3个,放入分好的3组,有A种放法,
则有(CCC++C)×A=2160种放法.
21.设m,n∈N,f(x)=(1+x)m+(1+x)n.
(1)当m=n=5时,若,求a0+a2+a4的值;
(2)f(x)展开式中x的系数是9,当m,n变化时,求x2系数的最小值.
解:(1)当m=n=5时,f(x)=2(1+x)5,令x=0时,f(0)=a5+a4+…+a1+a0=2,
令x=2时,f(2)=﹣a5+a4+…﹣a1+a0=2×35,
相加可得:a0+a2+a4==244.
(2)由题意可得:=m+n=9.
x2系数=====+.
又m,n∈N,∴m=4或5,其最小值为16.
即或时,x2系数的最小值为16.
22.设n∈N*,且n≥3,记集合M={1,2,3,…,n}的所有3个元素的子集为A1,A2,…,,mi为Ai中的最大元素,i=1,2,……,.
(1)当n=4时,求m1+m2+m3+m4的值;
(2)求m1+m2+…+的值.
解:(1)当n=4时,A1={1,2,3},A2={1,2,4},A3={1,3,4},A4={2,3,4},∴m1+m2+m3+m4=3+4+4+4=15.
故m1+m2+m3+m4的值为15;
(2)当n≥3时,集合M={1,2,3, ,n},所有3个元素的子集为:A1={1,2,3},A2={1,2,4},A3={1,3,4},A4={2,3,4},…,={1,2,3, ,n},
∴当最大元素为3时,共有个集合;
当最大元素为4时,共有个集合;
当最大元素为5时,共有个集合;
当最大元素为n时,共有个集合.
∴m1+m2+…+=3+4+5+…+n.
又∵(r+1)=(r+1)=3=3,r=2,3, ,n﹣1,
∴m1+m2+…+=3(+++ +)=3=.
故m1+m2+…+的值为:.
第六章 计数原理 章末综合测试
选择性必修第三册高中数学人教A版(2019)
考试范围:选择性必修第三册第六章 计数原理 ;考试满分:150分
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.的二项展开式中的常数项是( )
A.﹣20 B.﹣15 C.15 D.20
2.为培养学生的兴趣爱好,丰富学生的课余生活,某校团委开设了70个社团供学生自由选择.现已知甲、乙两位同学均准备从“创客空间”、“春柳文学社”、“舞龙协会”这三个社团中选择一个报名,则这两位同学的不同报名方案种数为( )
A.6 B.8 C.9 D.12
3.今天是星期五,经过7天后还是星期五,那么经过8100天后是( )
A.星期三 B.星期四 C.星期五 D.星期六
4.在(1﹣x)(2﹣x)(3﹣x)(4﹣x)(5﹣x)的展开式中,x4的系数为( )
A.15 B.﹣15 C.11 D.﹣11
5.已知电影院有三部影片同时上映,一部动画片,一部喜剧片,一部动作片,5名同学前去观看,若喜剧片和动作片各至少两人观看,则不同的观影方案共有( )种.
A.30 B.40 C.50 D.80
6.设n∈N*,xn=a0+a1(x﹣1)+ +an(x﹣1)n=b0+b1(x﹣2)+ +bn(x﹣2)n,则( )
A.b0﹣a0+b1﹣a1+ +bn﹣an=3n﹣2n
B.=2(a0+a1+ +an)
C.a0+a1+ +an=(a0+a1+ +an)
D.b1+4b2+ +n2bn=(a0+a1+ +an)
7.若(1﹣ax+x2)(1﹣x)8的展开式中含x2的项的系数为21,则a=( )
A.﹣3 B.﹣2 C.﹣1 D.1
8.为了进一步提高广大市民的生态文明建设意识,某市规定每年4月25日为“创建文明城 生态志愿行”为主题的生态活动日.现有5名同学参加志愿活动,需要携带勾子、铁锹、夹子三种劳动工具,要求每人都要携带一个工具,并且要求:带一个勾子,铁锹至少带2把,夹子至少带一个,则不同的安排方案共有( )
A.50种 B.60种 C.70种 D.80种
第Ⅱ卷
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.用0、1、2、3、4这五个数字组成无重复数字的自然数,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301、423等都是“凹数”,则下列结论中正确的是( )
A.组成的三位数的个数为60
B.在组成的三位数中,偶数的个数为30
C.在组成的三位数中,“凹数”的个数为20
D.在组成的三位数中,“凹数”的个数为24
10.若(x∈R),则下列判断正确的有( )
A.a0=1
B.
C.
D.
11.下列结论正确的是( )
A.
B.若,则
C.
D.
12.甲、乙、丙、丁、戊共5位志愿者被安排到A,B,C,D四所山区学校参加支教活动,要求每所学校至少安排一位志愿者,且每位志愿者只能到一所学校支教,则下列结论正确的是( )
A.不同的安排方法共有240种
B.甲志愿者被安排到A学校的概率是
C.若A学校安排两名志愿者,则不同的安排方法共有120种
D.在甲志愿者被安排到A学校支教的前提下,A学校有两名志愿者的概率是
三、填空题:本题共4小题,每小题5分,共20分。
13.2022年北京冬奥会期间,为了保障运动员健康,需要从北京某医院运动损伤科的5名男医生(含1名主任医师)、3名女医生(含1名主任医师)中分别选派3名男医生和2名女医生,要求至少有一名主任医师参加,则不同的选派方案共有 种.(用数字作答)
14.(a+)3+(a﹣)4的展开式中的系数为 (用数字作答).
15.某大学一寝室4人参加疫情防控讲座,4人就坐在一排有13个空位的座位上,根据防疫要求,任意两人之间需间隔1米以上(两个空位),则不同的就坐方法有 种.
16.已知,则a1+a2+a3+ +a2020的值为 ;a1+2a2+3a3+ +2020a2020的值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(1)解不等式.
(2)若,求正整数n.
18.“渐升数”是指除最高数位上的数字外,其余每一个数字均比其左边的数字大的正整数(如13456和35678都是五位“渐升数”).
(1)求五位“渐升数”的个数;
(2)如果把所有的五位“渐升数”按照从小到大的顺序排列,求第120个五位“渐升数”.
19.从7名男生5名女生中选取5人,分别求符合下列条件的选法有多少种?
(1)其中的A,B必须当选;
(2)A,B恰有一人当选;
(3)选取3名男生和2名女生分别担任班长、体育委员等5种不同职务,但体育委员必须由男生担任,班长必须由女生担任.
20.按照下列要求,分别求有多少种不同的方法?(列式并用数字作答)
(1)5个不同的小球放入4个不同的盒子,每个盒子至少放一个小球;
(2)6个不同的小球放入4个不同的盒子,每个盒子至少一个小球;
(3)6个相同的小球放入4个不同的盒子,每个盒子至少一个小球
(4)6个不同的小球放入4个不同的盒子,恰有1个空盒.
21.设m,n∈N,f(x)=(1+x)m+(1+x)n.
(1)当m=n=5时,若,求a0+a2+a4的值;
(2)f(x)展开式中x的系数是9,当m,n变化时,求x2系数的最小值.
22.设n∈N*,且n≥3,记集合M={1,2,3,…,n}的所有3个元素的子集为A1,A2,…,,mi为Ai中的最大元素,i=1,2,……,.
(1)当n=4时,求m1+m2+m3+m4的值;
(2)求m1+m2+…+的值.
第六章 计数原理 章末综合测试
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.的二项展开式中的常数项是( )
A.﹣20 B.﹣15 C.15 D.20
解:展开式第r+1项:
,
3﹣=0,可得r=2时,
的二项展开式中的常数项是,
故选:C.
2.为培养学生的兴趣爱好,丰富学生的课余生活,某校团委开设了70个社团供学生自由选择.现已知甲、乙两位同学均准备从“创客空间”、“春柳文学社”、“舞龙协会”这三个社团中选择一个报名,则这两位同学的不同报名方案种数为( )
A.6 B.8 C.9 D.12
解:不妨记“创客空间”、“春柳文学社”、“舞龙协会”分别为a、b、c,
则这两位同学的报名方案有aa,ab,ac,ba,bb,bc,ca,cb,cc,共9种.
故选:C.
3.今天是星期五,经过7天后还是星期五,那么经过8100天后是( )
A.星期三 B.星期四 C.星期五 D.星期六
解:8100=(7+1)100=7100+C799+C798+...+C7+1,
因为7100+C799+C798+...+C7能被7整除,所以8100除以7的余数为1,
故经过8100天后是星期六.
故选:D.
4.在(1﹣x)(2﹣x)(3﹣x)(4﹣x)(5﹣x)的展开式中,x4的系数为( )
A.15 B.﹣15 C.11 D.﹣11
解:展开式中含x4的项为:
在1﹣x,2﹣x,3﹣x,4﹣x,5﹣x这5个代数式中4个取﹣x,其余1个代数式取常数,
∴展开式中x4的系数为1+2+3+4+5=15,
故选:A.
5.已知电影院有三部影片同时上映,一部动画片,一部喜剧片,一部动作片,5名同学前去观看,若喜剧片和动作片各至少两人观看,则不同的观影方案共有( )种.
A.30 B.40 C.50 D.80
解:由题可知共有三类:①2人看喜剧片,2人看动作片,1人看动画片,方案数为:=30;
②3人看喜剧片,2人看动作片,0人看动画片,方案数为:=10;
③2人看喜剧片,3人看动作片,0人看动画片,方案数为:=10,
共有30+10+10=50种方案.
故选:C.
6.设n∈N*,xn=a0+a1(x﹣1)+ +an(x﹣1)n=b0+b1(x﹣2)+ +bn(x﹣2)n,则( )
A.b0﹣a0+b1﹣a1+ +bn﹣an=3n﹣2n
B.=2(a0+a1+ +an)
C.a0+a1+ +an=(a0+a1+ +an)
D.b1+4b2+ +n2bn=(a0+a1+ +an)
解:由二项式定理知:
xn=[(x﹣1)+1]n=C+C(x﹣1)+C(x﹣1)2+ +C(x﹣1)n,
∴ai=C(i=0,1,2...n),令x=2,则有a0+a1+ +an=2n;
xn=[(x﹣2)+2]n=C 2n+C 2n﹣1 (x﹣2)+C 2n﹣2 (x﹣2)2+ +C(x﹣2)n,
∴bi=C2n﹣i (i=0,1,2,...,n),令x=3,则有b0+b1+ +bn=3n;
故有b0﹣a0+b1﹣a1+ +bn﹣an=3n﹣2n,A正确;
令n=2,则有a0=1,a1=2,a2=1,b0=4,b1=4,b2=1,
分别代入B,C,D选项:
=4+2+1=7,2(a0+a1+a2)=8,B错误;
a0+a1+a2=1+1+=,(a0+a1+a2)=,C错误;
b1+4b2=4+4=8,(a0+a1+a2)=6,D错误;
故选:A.
7.若(1﹣ax+x2)(1﹣x)8的展开式中含x2的项的系数为21,则a=( )
A.﹣3 B.﹣2 C.﹣1 D.1
解:分三种情况:
(1)当因式(1﹣ax+x2)中取1时,含x2的项为,其系数为28;
(2)当因式(1﹣ax+x2)中取﹣ax时,含x2的项为(﹣ax) ,其系数为8a;
(3)当因式(1﹣ax+x2)中取x2时,含x2的项为x2 ,其系数为1,
所以展开式中含x2的项的系数为28+8a+1=21,解得a=﹣1.
故选:C.
8.为了进一步提高广大市民的生态文明建设意识,某市规定每年4月25日为“创建文明城 生态志愿行”为主题的生态活动日.现有5名同学参加志愿活动,需要携带勾子、铁锹、夹子三种劳动工具,要求每人都要携带一个工具,并且要求:带一个勾子,铁锹至少带2把,夹子至少带一个,则不同的安排方案共有( )
A.50种 B.60种 C.70种 D.80种
解:携带工具方案有两类:
第一类,1个勾子,1个夹子,3把铁锹,所以携带工具的方案数有=20种;
第二类,1个勾子,2个夹子,2把铁锹,所以携带工具的方案数有CC=30种;
所以不同的安排方案共有20+30=50种.
故选:A.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.用0、1、2、3、4这五个数字组成无重复数字的自然数,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301、423等都是“凹数”,则下列结论中正确的是( )
A.组成的三位数的个数为60
B.在组成的三位数中,偶数的个数为30
C.在组成的三位数中,“凹数”的个数为20
D.在组成的三位数中,“凹数”的个数为24
解:用0、1、2、3、4这五个数字组成无重复数字的自然数,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,
对于A,因为百位数上的数字不能为零,所以组成的三位数的个数为,故A不正确;
对于B,将三位数的偶数分为两类,①个位数为0,则有种,②个位数为2或4,则有=2×3×3=18种,
所以在组成的三位数中,偶数的个数为12+18=30,故B正确;
对于C、D,将这些“凹数”分为三类,①十位为0,则有种,
②十位为1,则有种,
③十位为2,则有种,
所以在组成的三位数中,“凹数”的个数为12+6+2=20,故C正确,D不正确.
故选:BC.
10.若(x∈R),则下列判断正确的有( )
A.a0=1
B.
C.
D.
解:由题意,当x=0时,a0=12009=1,
当x=1时,a0+a1+a2+a3+…+a2009=( 1)2009= 1,
当x=﹣1时,a0﹣a1+a2﹣a3+…﹣a2009=32009,
所以,a0+a2+a4+…+a2008=,
,
故选:ACD.
11.下列结论正确的是( )
A.
B.若,则
C.
D.
解:对于A,=(1+2)50=350,故A正确;
对于B,若,
则令x=﹣1,可得a0﹣a1+a2﹣a3+…+a50=,故B正确;
对于C,因为m===n,即m=n,
所以+3+5+ +101=+++ ++2+4+ +100
=250+2(+2+ +50)=250+2(50+50+…+50)
=250+2×50×249=51×250,故C错误;
对于D,因为m=n,所以
=50(++…+),
而++…+=++…++=×249,
所以=50××249=25×249,故D正确.
故选:ABD.
12.甲、乙、丙、丁、戊共5位志愿者被安排到A,B,C,D四所山区学校参加支教活动,要求每所学校至少安排一位志愿者,且每位志愿者只能到一所学校支教,则下列结论正确的是( )
A.不同的安排方法共有240种
B.甲志愿者被安排到A学校的概率是
C.若A学校安排两名志愿者,则不同的安排方法共有120种
D.在甲志愿者被安排到A学校支教的前提下,A学校有两名志愿者的概率是
解:甲、乙、丙、丁、戊共5位志愿者被安排到A,B,C,D四所山区学校参加支教活动,
则共有种安排方法,故A正确;
甲志愿者被安排到A学校,
若A学校只有一个人,则有种安排方法,
若A学校只有2个人,则有种安排方法,
所以甲志愿者被安排到A学校有36+24=60种安排方法,
所以甲志愿者被安排到A学校的概率是,故B正确;
若A学校安排两名志愿者,则不同的安排方法共有种,故C错误;
甲志愿者被安排到A学校有60种安排方法,
在甲志愿者被安排到A学校支教的前提下,A学校有两名志愿者的安排方法有24种,
所以在甲志愿者被安排到A学校支教的前提下,A学校有两名志愿者的概率是,故D正确.
故选:ABD.
三、填空题:本题共4小题,每小题5分,共20分。
13.2022年北京冬奥会期间,为了保障运动员健康,需要从北京某医院运动损伤科的5名男医生(含1名主任医师)、3名女医生(含1名主任医师)中分别选派3名男医生和2名女医生,要求至少有一名主任医师参加,则不同的选派方案共有 26 种.(用数字作答)
解:根据题意,从5名男医生(含一名主任医师)、3名女医生(含一名主任医师)中分别选派3名男医生和2名女医生,
共有CC=10×3=30种选派方案,
如果所选的男女主任都没有参加,共有C×C=4种选派方案,
所以至少有一名主任医师参加有30﹣4=26种,
故答案为:26.
14.(a+)3+(a﹣)4的展开式中的系数为 9 (用数字作答).
解:对于,根据二项展开式:,
当r=1时,系数为;
对于,根据二项展开式:,
当r=2时,系数为;
故(a+)3+(a﹣)4的展开式中的系数为3+6=9.
故答案为:9.
15.某大学一寝室4人参加疫情防控讲座,4人就坐在一排有13个空位的座位上,根据防疫要求,任意两人之间需间隔1米以上(两个空位),则不同的就坐方法有 840 种.
解:先假设每人坐一个位置相当于去掉4个位置,再将4人中间任意两人之间放进2个空位,
此时空位一共还剩3个,若将这三个连在一起插入4人之间和两侧的空位上,有5种放法;
若将这三个分成两组,一组两个,一组一个,插入4人之间和两侧的空位上,有种放法;
若将这三个分成三组插入4人之间和两侧的空位上,有种放法,
故不同的就坐方法为种.
故答案为:840.
16.已知,则a1+a2+a3+ +a2020的值为 ﹣1 ;a1+2a2+3a3+ +2020a2020的值为 0 .
解:令x=0,则a0=1,
令x=1,则a0+a1+a2+a3+ +a2020=0,
∴a1+a2+a3+ +a2020=﹣1,
∵,
∴f′(x)=﹣2020(1﹣x)1999=a1+2a2x+3a3x2+ +2020a2020x1999,
令x=1,则a1+2a2+3a3+ +2020a2020=0,
故答案为:﹣1;0.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(1)解不等式.
(2)若,求正整数n.
解:(1),
则,
则(10﹣x)(9﹣x)<6,
即7<x<12,
又,
即x=8,
即不等式的解集为{8};
(2)已知,
则,
即n(n﹣1)(n﹣2)=364×6=14×13×12,
即n=14.
18. “渐升数”是指除最高数位上的数字外,其余每一个数字均比其左边的数字大的正整数(如13456和35678都是五位“渐升数”).
(1)求五位“渐升数”的个数;
(2)如果把所有的五位“渐升数”按照从小到大的顺序排列,求第120个五位“渐升数”.
解:(1)根据题意,五位“渐升数”要求除万位数字之外,每一个数字均比其左边的数字大,
故要求的五位“渐升数”中不能有0.
只需在其他9个数字中任取5个,将其从小到大排列,即可得一个五位“渐升数”,故每种取法对应1个“渐升数”,
则五位“渐升数”共有个
(2)对于所有的五位“渐升数”,1在最高数位的有个,
2在最高数位的有个,
3在最高数位的有个,
因为70+35+15=120,
所以第120个“渐升数”是最高数位为3的最大的五位“渐升数”,为36789.
19.从7名男生5名女生中选取5人,分别求符合下列条件的选法有多少种?
(1)其中的A,B必须当选;
(2)A,B恰有一人当选;
(3)选取3名男生和2名女生分别担任班长、体育委员等5种不同职务,但体育委员必须由男生担任,班长必须由女生担任.
解:(1)根据题意,先选出A,B,再从剩下的10人中选3人,
共有种选法;
(2)根据题意,先在AB中选出1人,再从剩下的10人中选4人,
共有种选法;
(3)根据题意,选出一名男生担任体育委员共有种情况,
选出一名女生担任班长共有种情况.
剩下6名男生再选2人,4名女生再选1人,担任其它3个班委,共有种情况,
所以共有种选法.
20.按照下列要求,分别求有多少种不同的方法?(列式并用数字作答)
(1)5个不同的小球放入4个不同的盒子,每个盒子至少放一个小球;
(2)6个不同的小球放入4个不同的盒子,每个盒子至少一个小球;
(3)6个相同的小球放入4个不同的盒子,每个盒子至少一个小球
(4)6个不同的小球放入4个不同的盒子,恰有1个空盒.
解:(1)根据题意,先将5个小球分为4组,再将4组放入4个盒子即可,
有种放法;
(2)根据题意,先将6个小球分为4组,有+C种分组方法,
再将4组放入4个盒子,有A种放法,
则有(+C)×A=1560种放法;
(3)根据题意,由于小球相同,将6个小球分为4组,依次放入4个盒子即可,
利用挡板法分析:将6个小球排成一排,中间有5个空位,
在其中任选3个空位,插入挡板,可以将6个小球分为4组,
进而依次放入4个盒子,有C=10种放法;
(4)根据题意,先将6个小球分为3组,有CCC++C种分组方法,
再从4个盒子中任选3个,放入分好的3组,有A种放法,
则有(CCC++C)×A=2160种放法.
21.设m,n∈N,f(x)=(1+x)m+(1+x)n.
(1)当m=n=5时,若,求a0+a2+a4的值;
(2)f(x)展开式中x的系数是9,当m,n变化时,求x2系数的最小值.
解:(1)当m=n=5时,f(x)=2(1+x)5,令x=0时,f(0)=a5+a4+…+a1+a0=2,
令x=2时,f(2)=﹣a5+a4+…﹣a1+a0=2×35,
相加可得:a0+a2+a4==244.
(2)由题意可得:=m+n=9.
x2系数=====+.
又m,n∈N,∴m=4或5,其最小值为16.
即或时,x2系数的最小值为16.
22.设n∈N*,且n≥3,记集合M={1,2,3,…,n}的所有3个元素的子集为A1,A2,…,,mi为Ai中的最大元素,i=1,2,……,.
(1)当n=4时,求m1+m2+m3+m4的值;
(2)求m1+m2+…+的值.
解:(1)当n=4时,A1={1,2,3},A2={1,2,4},A3={1,3,4},A4={2,3,4},∴m1+m2+m3+m4=3+4+4+4=15.
故m1+m2+m3+m4的值为15;
(2)当n≥3时,集合M={1,2,3, ,n},所有3个元素的子集为:A1={1,2,3},A2={1,2,4},A3={1,3,4},A4={2,3,4},…,={1,2,3, ,n},
∴当最大元素为3时,共有个集合;
当最大元素为4时,共有个集合;
当最大元素为5时,共有个集合;
当最大元素为n时,共有个集合.
∴m1+m2+…+=3+4+5+…+n.
又∵(r+1)=(r+1)=3=3,r=2,3, ,n﹣1,
∴m1+m2+…+=3(+++ +)=3=.
故m1+m2+…+的值为:.
