第九章 统计 章末综合测试-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含解析)
文档属性
| 名称 | 第九章 统计 章末综合测试-2022-2023学年高一下学期数学人教A版(2019)必修第二册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 460.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 00:00:00 | ||
图片预览




文档简介
绝密★启用前
第九章 统计 章末综合测试
必修第二册高中数学人教A版(2019)
考试范围:必修第二册第九章 统计;考试满分:150分
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
第Ⅰ卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某学校想了解高一学生社会实践项目的选择意向,采用分层抽样的方式抽取100人进行问卷调查.已知高一年级有270名男生,从男生中抽取了60名,则该校高一年级共有学生( )
A.445人 B.450人 C.520人 D.540人
2.从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出90户调查社会购买力的某一项指标,应采用的最佳抽样方法是( )
A.按家庭分层抽样 B.按收入分层抽样
C.简单随机抽样 D.各种方法均可
3.要考察某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,…499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则第四袋牛奶的标号是( )
(下面摘取了某随机数表的第7行至第9行)
84421 75531 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98301 07185 12867 35807 44395 23879 33211
A.358 B.301 C.071 D.206
4.某日某火锅店进货了四种食品,其中毛肚、鸭肠、牛肉及莴笋分别进货了700份、600份、500份、200份,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的毛肚份数与莴笋份数之和是( )
A.7 B.13 C.8 D.9
5.某单位为了解该单位党员开展学习党史知识活动情况,随机抽取了部分党员,对他们一周的党史学习时间进行了统计,统计数据如下表所示:
党史学习时间(小时) 7 8 9 10 11
党员人数 6 10 9 7 8
则该单位党员一周学习党史时间的众数及第50百分位数分别是( )
A.8,8.5 B.8,8 C.9,8 D.8,9
6.已知数据x1,x2,…xn是某市n(n≥3,n∈N*)个普通职工的年收入,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是( )
A.年收入的平均数可能不变,中位数可能不变,方差可能不变
B.年收入的平均数大大增加,中位数可能不变,方差变大
C.年收入的平均数大大增加,中位数可能不变,方差也不变
D.年收入的平均数大大增加,中位数一定变大,方差可能不变
7.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图(如图),则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980﹣1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事产品岗位的90后人数超过总人数的5%
D.互联网行业中从事运营岗位的90后人数比80前从事互联网行业的人数多
8.已知一组数据x1,x2, ,xn的平均数为,标准差为s.若3x1﹣2,3x2﹣2, ,3xn﹣2的平均数与方差相等,则的最大值为( )
A. B. C. D.﹣2
第Ⅱ卷(非选择题)
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知数据x1,x2,x3,…,xn的众数、平均数、方差、第80百分位数分别是a1,b1,c1,d1,数据y1,y2,y3,…,yn的众数、平均数、方差、第80百分位数分别是a2,b2,c2,d2,且满足yi=3xi﹣1(i=1,2,3, ,n),则下列结论正确的是( )
A.b2=3b1﹣1 B.a2=a1 C.c2=9c1 D.d2=3d1﹣1
10.为推动学校体育运动发展,引导学生积极参与体育锻炼,增强健康管理意识,某校根据性别比例采用分层抽样方法随机抽取了120名男生和80名女生,调查并分别绘制出男、女生每天在校平均体育活动时间的频率分布直方图(如图所示),则( )
A.a=0.010
B.该校男生每天在校平均体育活动时间中位数的估计值为75
C.估计该校至少有一半学生每天在校平均体育活动时间超过一小时
D.估计该校每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为3:1
11.四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的有( )
A.中位数为3,众数为3 B.平均数为3,众数为4
C.平均数为3,中位数为3 D.平均数为2,方差为2.4
12.关于用统计方法获取数据,分析数据,下列结论正确的是( )
A.某食品加工企业为了解生产的产品是否合格,合理的调查方式为抽样调查
B.为了解高一学生的视力情况,现有高一男生480人,女生420人,按性别进行分层抽样,样本量按比例分配,若从女生中抽取的样本量为63,则样本容量为135
C.若甲、乙两组数据的标准差满足s甲<s乙,则可以估计乙比甲更稳定
D.若数据x1,x2,x3,…,xn的平均数为,则数据yi=axi﹣b(i=1,2,3,…,n)的平均数为a﹣b
三、填空题:本题共4小题,每小题5分,共20分。
13.若一组数据a1,a2,a3,…,an的方差为4,则3a1﹣1,3a2﹣1,3a3﹣1,…,3an﹣1的标准差为 .
14.用样本估计总体的统计思想在我国古代数学名著《数书九章》中就有记载,其中有道“米谷粒分”题:粮仓开仓收粮,有人送来米1600石,验得米内夹谷,抽样取米一把,数得250粒内夹谷25粒,估计这批米内所夹的谷有 石.
15.某校抽取100名学生测身高,其中身高最大值为186cm,最小值为154cm,根据身高数据绘制频率组距分布直方图,组距为5,且第一组下限为153.5,则组数为 .
16.由8个整数形成的样本数据中,至少有六个互不相同的整数,若平均数、中位数、唯一的众数和全距(即样本中最大数与最小数之差)都是8,则可能成为样本数据中的最大整数是 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.立德中学高一年级某学生社团开展了“使用移动支付平台——支付宝与微信支付的对比分析”的课题研究.随机调查了1000名市民,结果显示:使用支付宝的有456人,使用微信支付的有783人,两种都使用的有298人.
(1)只使用支付宝不使用微信支付的有多少人?
(2)两种移动支付方式都不使用的有多少人?(要有合理的说明过程)
18.某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛的得分情况如下:
甲:15,17,14,23,22,24,32;
乙:12,13,11,23,27,31,30.
(1)分别计算甲、乙两名运动员得分的平均数;
(2)分别计算甲、乙两名运动员得分的方差,并判断哪位运动员的成绩更稳定?
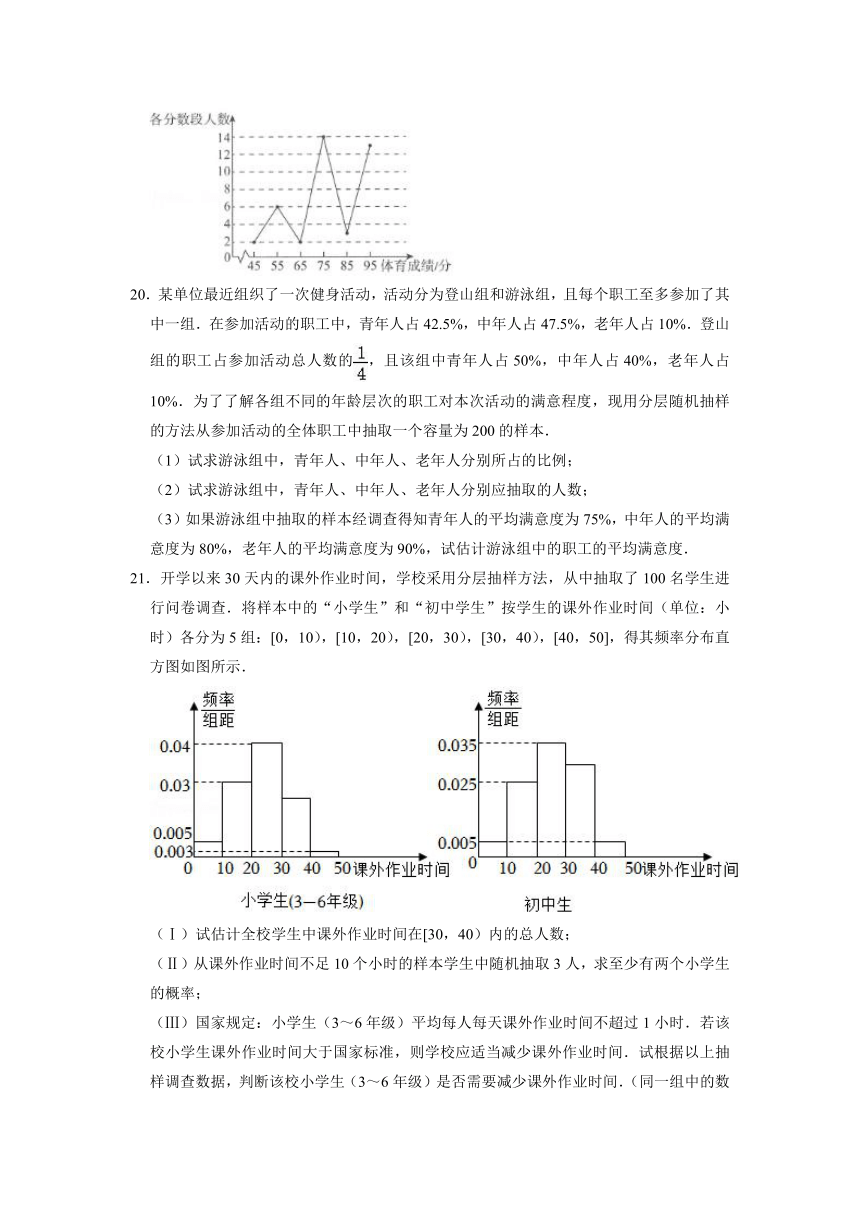
19.某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,得到体育成绩的折线图如图所示.
(1)若体育成绩大于或等于70分的学生为“体育良生”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良生”的人数;
(2)用样本估计总体的思想,试估计该校高一年级学生达标测试的平均分;
(3)假设甲、乙、丙三人的体育成绩分别为a、b、c,且a∈[70,80),b∈[80,90),c∈[90,100],当三人的体育成绩方差s2最小时,写出a、b、c的所有可能取值.(不要求证明)
20.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.
(1)试求游泳组中,青年人、中年人、老年人分别所占的比例;
(2)试求游泳组中,青年人、中年人、老年人分别应抽取的人数;
(3)如果游泳组中抽取的样本经调查得知青年人的平均满意度为75%,中年人的平均满意度为80%,老年人的平均满意度为90%,试估计游泳组中的职工的平均满意度.
21.开学以来30天内的课外作业时间,学校采用分层抽样方法,从中抽取了100名学生进行问卷调查.将样本中的“小学生”和“初中学生”按学生的课外作业时间(单位:小时)各分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],得其频率分布直方图如图所示.
(Ⅰ)试估计全校学生中课外作业时间在[30,40)内的总人数;
(Ⅱ)从课外作业时间不足10个小时的样本学生中随机抽取3人,求至少有两个小学生的概率;
(Ⅲ)国家规定:小学生(3~6年级)平均每人每天课外作业时间不超过1小时.若该校小学生课外作业时间大于国家标准,则学校应适当减少课外作业时间.试根据以上抽样调查数据,判断该校小学生(3~6年级)是否需要减少课外作业时间.(同一组中的数据用该组区间的中点值作代表)
22.随着手机和网络的普及,外卖行业得到迅速的发展.某外卖平台为了解某地区用户对其提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:
用户编号 评分 用户编号 评分 用户编号 评分 用户编号 评分
1 78 11 88 21 79 31 93
2 73 12 86 22 83 32 78
3 81 13 95 23 72 33 75
4 92 14 76 24 74 34 81
5 95 15 97 25 91 35 84
6 85 16 78 26 66 36 77
7 79 17 88 27 80 37 81
8 84 18 82 28 83 38 76
9 63 19 76 29 74 39 85
10 86 20 89 30 82 40 89
(1)请你估计该地区所有用户评分的25%,95%分位数;
(2)若从这40个用户中抽取一个容量为10的样本,且抽到的10个用户的评分分别为92,84,86,78,89,74,83,78,77,89,试计算这10个数据的平均数和方差s2;
(3)在(2)的条件下,若用户的满意度评分在内,则满意度等级为“A级”,试用样本估计总体的思想,根据所抽到的10个数据,估计该地区满意度等级为“A级”的用户所占的百分比.
(参考数据:,,)
第九章 统计 章末综合测试
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某学校想了解高一学生社会实践项目的选择意向,采用分层抽样的方式抽取100人进行问卷调查.已知高一年级有270名男生,从男生中抽取了60名,则该校高一年级共有学生( )
A.445人 B.450人 C.520人 D.540人
解:由题意计算抽样比例为=,
所以该校高一年级共有学生270×=450(人).
故选:B.
2.从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出90户调查社会购买力的某一项指标,应采用的最佳抽样方法是( )
A.按家庭分层抽样 B.按收入分层抽样
C.简单随机抽样 D.各种方法均可
解:因为社会购买力的某项指标受到家庭收入的影响,
而社区中各个家庭收入差别明显,
故应采用的最佳抽样方法是分层抽样.
故选:B.
3.要考察某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,…499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则第四袋牛奶的标号是( )
(下面摘取了某随机数表的第7行至第9行)
84421 75531 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98301 07185 12867 35807 44395 23879 33211
A.358 B.301 C.071 D.206
解:由题意可知,读取的第一个数据是583,不符合条件,第二个数据是921,不符合条件,第三个数据是206,符合条件,
即随机选取的第一袋牛奶标号是206,
以下数据依次是766,301,647,859,169,555,671,998,301,其中符合题意的数据只有301,169,301三个数据,但是301属于重复数据,继续往后计数,下一个数是071,符合条件,即前四袋牛奶的标号依次为206,301,169,071,
所以第四袋牛奶的标号为071.
故选:C.
4.某日某火锅店进货了四种食品,其中毛肚、鸭肠、牛肉及莴笋分别进货了700份、600份、500份、200份,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的毛肚份数与莴笋份数之和是( )
A.7 B.13 C.8 D.9
解:由题意,抽样的比例为=,
则应抽取的毛肚份数与莴笋份数之和为(700+200)×=9,
故选:D.
5.某单位为了解该单位党员开展学习党史知识活动情况,随机抽取了部分党员,对他们一周的党史学习时间进行了统计,统计数据如下表所示:
党史学习时间(小时) 7 8 9 10 11
党员人数 6 10 9 7 8
则该单位党员一周学习党史时间的众数及第50百分位数分别是( )
A.8,8.5 B.8,8 C.9,8 D.8,9
解:由图表可知众数为8,
共6+10+9+7+8=40人,
40×50%=20,
所以第50百分位数为9.
故选:D.
6.已知数据x1,x2,…xn是某市n(n≥3,n∈N*)个普通职工的年收入,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是( )
A.年收入的平均数可能不变,中位数可能不变,方差可能不变
B.年收入的平均数大大增加,中位数可能不变,方差变大
C.年收入的平均数大大增加,中位数可能不变,方差也不变
D.年收入的平均数大大增加,中位数一定变大,方差可能不变
解:因为数据x1,x2,x3,…,xn是普通职工n(n≥3,n∈N*)个人的年收入,
而xn+1为世界首富的年收入
则xn+1会远大于x1,x2,x3,…,xn,
故这n+1个数据中,年收入平均数大大增大,中位数可能不变,也可能稍微变大,
由于数据的集中程度也受到xn+1比较大的影响,而更加离散,则方差变大.
故选:B.
7.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图(如图),则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980﹣1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事产品岗位的90后人数超过总人数的5%
D.互联网行业中从事运营岗位的90后人数比80前从事互联网行业的人数多
解:由整个互联网行业从业者年龄分布饼状图知,
互联网行业从业人员中90后占56%,
故选项A不符合题意;
∵56%×39.6%≈22.17%,
∴互联网行业中从事技术岗位的人数超过总人数的20%,
故选项B不符合题意;
∵56%×6.5%=3.64%,
∴互联网行业中从事产品岗位的90后人数不到总人数的5%,
故选项C符合题意;
∵56%×17%=9.52%,
∴互联网行业中从事运营岗位的90后人数占总人数的9.52%,
而80前从事互联网行业的人数占总人数的3%,
故互联网行业中从事运营岗位的90后人数比80前从事互联网行业的人数多,
故选项D不符合题意.
故选:C.
8.已知一组数据x1,x2, ,xn的平均数为,标准差为s.若3x1﹣2,3x2﹣2, ,3xn﹣2的平均数与方差相等,则的最大值为( )
A. B. C. D.﹣2
解:由题意可得3﹣2=9s2,则s=.因为s2≥0,所以3﹣2≥0,解得.
令y=s﹣=﹣().
设t=,则=(t≥0),
从而=≤﹣,故.
故选:A.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知数据x1,x2,x3,…,xn的众数、平均数、方差、第80百分位数分别是a1,b1,c1,d1,数据y1,y2,y3,…,yn的众数、平均数、方差、第80百分位数分别是a2,b2,c2,d2,且满足yi=3xi﹣1(i=1,2,3, ,n),则下列结论正确的是( )
A.b2=3b1﹣1 B.a2=a1 C.c2=9c1 D.d2=3d1﹣1
解:由题意可知,两组数据满足yi=3xi﹣1(i=1,2,3, ,n),
由平均数计算公式得×(y1+y2+...+yn)=×[(3x1﹣1)+(3x2﹣1)+…+(3xn﹣1)]=3××(x1+x2+…+xn)﹣1,
所以b2=3b1﹣1,故A正确;
由它们的众数也满足yi=3xi﹣1(i=1,2,3, ,n),
则有a2=3a1﹣1,故B错误;
由方差的性质得c2=9c1,故C正确;
对于数据x1,x2,x3,…,xn,假设其第80百分位数为d1,
当0.8n=k是整数时,d1=,
当0.8n不是整数时,设其整数部分为k,则d1=xk+1,
所以对于数据3x1﹣1,3x2﹣1,3x3﹣1,…,3xn﹣1,假设其第80百分位数为d2,
当0.8n=k是整数时,d2==3d1﹣1,
当0.8n不是整数时,设其整数部分为k,则d2=3xk+1﹣1=3d1﹣1,
所以d2=3d1﹣1,故D正确.
故选:ACD.
10.为推动学校体育运动发展,引导学生积极参与体育锻炼,增强健康管理意识,某校根据性别比例采用分层抽样方法随机抽取了120名男生和80名女生,调查并分别绘制出男、女生每天在校平均体育活动时间的频率分布直方图(如图所示),则( )
A.a=0.010
B.该校男生每天在校平均体育活动时间中位数的估计值为75
C.估计该校至少有一半学生每天在校平均体育活动时间超过一小时
D.估计该校每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为3:1
解:对于A,10a+10×0.020+10×0.035+10×0.020+10a+10×0.005=1,解得,a=0.010,
对于B,a=0.010,前两个小矩形面积之和为0.3,即中位数在[60,70)内,设为m,
则,解得,
该校男生每天在校平均体育活动时间中位数的估计值为65.7,
对于C,根据频率分布直方图可得,男生中每天在校平均体育活动时间超过一小时的频率为10×(0.035+0.020+0.010+0.005)=0.700,
人数为120×0.7=84,
女生中每天在校平均体育活动时间超过一小时的频率为10×(0.030+0.010+0.005)=0.450,人数为80×0.450=36,
故学生每天在校平均体育活动时间超过一小时的频率为,
故该校至少有一半学生每天在校平均体育活动时间超过一小时,
对于D,男生中每天在校平均体育活动时间不低于80分钟的频率为10×(0.010+0.005)=0.15,人数为120×0.15=18,
女生中每天在校平均体育活动时间不低于80分钟的频率为10×0.005=0.050,人数为80×0.050=4,
所以每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为,
所以该校每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为9:2.
故选:AC.
11.四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的有( )
A.中位数为3,众数为3 B.平均数为3,众数为4
C.平均数为3,中位数为3 D.平均数为2,方差为2.4
解:对于A,当掷骰子出现的结果为1,2,3,3,6时,
满足中位数为3,众数为3,所以A不可以判断;
对于B,若平均数为3,且出现点数为6,则其余4个数的和为9,
而众数为4,故其余4个数的和至少为10,所以B可以判断;
对于C,当掷骰子出现的结果为1,1,3,4,6时,
满足平均数为3,中位数为3,可以出现点6,所以C不能判断;
对于D,若平均数为2,且出现点数6,
则方差S2>(6﹣2)2=3.2>2.4,
所以当平均数为2,方差为2.4时,一定不会出现点数6.
故选:BD.
12.关于用统计方法获取数据,分析数据,下列结论正确的是( )
A.某食品加工企业为了解生产的产品是否合格,合理的调查方式为抽样调查
B.为了解高一学生的视力情况,现有高一男生480人,女生420人,按性别进行分层抽样,样本量按比例分配,若从女生中抽取的样本量为63,则样本容量为135
C.若甲、乙两组数据的标准差满足s甲<s乙,则可以估计乙比甲更稳定
D.若数据x1,x2,x3,…,xn的平均数为,则数据yi=axi﹣b(i=1,2,3,…,n)的平均数为a﹣b
解:对于A,了解生产的产品是否合格,合理的调查 方式为抽样调查,故A正确;
对于B,根据分层抽样抽样比可知样本容量为×(480+420)=135,故B正确;
对于C,∵S甲<S乙,∴甲的数据更稳定,故C错误;
对于D,根据平均数的性质,yi=axi﹣b(i=1,2,3, ,n)的平均数为﹣b,故D正确.
故选:ABD.
三、填空题:本题共4小题,每小题5分,共20分。
13.若一组数据a1,a2,a3,…,an的方差为4,则3a1﹣1,3a2﹣1,3a3﹣1,…,3an﹣1的标准差为 6 .
解:因为a1,a2,a3,…,an的方差为4,
所以3a1﹣1,3a2﹣1,3a3﹣1,…,3an﹣1的方差为32×4=36,
所以3a1﹣1,3a2﹣1,3a3﹣1,…,3an﹣1的标准差为6.
故答案为:6.
14.用样本估计总体的统计思想在我国古代数学名著《数书九章》中就有记载,其中有道“米谷粒分”题:粮仓开仓收粮,有人送来米1600石,验得米内夹谷,抽样取米一把,数得250粒内夹谷25粒,估计这批米内所夹的谷有 160 石.
解:依题意,设这批米内所夹的谷有x石,
则,解得x=160,
所以估计这批米内所夹的谷有160石.
故答案为:160.
15.某校抽取100名学生测身高,其中身高最大值为186cm,最小值为154cm,根据身高数据绘制频率组距分布直方图,组距为5,且第一组下限为153.5,则组数为 7 .
解:极差为186﹣154=32,组距为5,且第一组下限为153.5,
=6.4,故组数为7组,
故答案为:7.
16.由8个整数形成的样本数据中,至少有六个互不相同的整数,若平均数、中位数、唯一的众数和全距(即样本中最大数与最小数之差)都是8,则可能成为样本数据中的最大整数是 12 .
解:依题意,平均数=中位数=众数=8,所以偏态系数为0,数据分布对称,
因为存在众数且众数唯一,
所以可设这8个整数为x1,x2,x3,8,8,x4,x5,x6,
且x1<x2<x3<8=8<x4<x5<x6,
所以,解得x6=12.
故答案为:12.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.立德中学高一年级某学生社团开展了“使用移动支付平台——支付宝与微信支付的对比分析”的课题研究.随机调查了1000名市民,结果显示:使用支付宝的有456人,使用微信支付的有783人,两种都使用的有298人.
(1)只使用支付宝不使用微信支付的有多少人?
(2)两种移动支付方式都不使用的有多少人?(要有合理的说明过程)
解:(1)因为“使用支付宝”的有456人,“两种支付方式都使用”的有298人,
所以“只使用支付宝不使用微信支付”的有456﹣298=158(人).
(2)同(1)有,“只使用微信支付不使用支付宝”的有783﹣298=485(人),
所以,“至少使用一种移动支付方式”的有485+158+298=941(人),
故“两种移动支付方式都不使用”有1000﹣941=59(人).
18.某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛的得分情况如下:
甲:15,17,14,23,22,24,32;
乙:12,13,11,23,27,31,30.
(1)分别计算甲、乙两名运动员得分的平均数;
(2)分别计算甲、乙两名运动员得分的方差,并判断哪位运动员的成绩更稳定?
解:(1)设甲、乙的平均分别记为,,
则,,
故甲、乙两名运动员得分的平均数均为21;
(2)设甲、乙两名运动员得分的方差分别为,
则=,=,
∵,
∴甲运动员的成绩更稳定.
19.某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,得到体育成绩的折线图如图所示.
(1)若体育成绩大于或等于70分的学生为“体育良生”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良生”的人数;
(2)用样本估计总体的思想,试估计该校高一年级学生达标测试的平均分;
(3)假设甲、乙、丙三人的体育成绩分别为a、b、c,且a∈[70,80),b∈[80,90),c∈[90,100],当三人的体育成绩方差s2最小时,写出a、b、c的所有可能取值.(不要求证明)
解:(1)根据折线图体育成绩大于或等于70分的学生有14+3+13=30(人),
所以该校高一年级学生“体育良生”的人数为(人).
(2)用样本估计总体的思想,估计该校高一年级学生达标测试的平均分为.
(3)由于甲、乙、丙三人的体育成绩分别为a,b,c,且a∈[70,80),b∈[80,90),其中a,b,c∈N,当三人的体育成绩方差s2最小时,a、b、c的所有可能取值79.84,90或79,85,90.
20.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.
(1)试求游泳组中,青年人、中年人、老年人分别所占的比例;
(2)试求游泳组中,青年人、中年人、老年人分别应抽取的人数;
(3)如果游泳组中抽取的样本经调查得知青年人的平均满意度为75%,中年人的平均满意度为80%,老年人的平均满意度为90%,试估计游泳组中的职工的平均满意度.
解:(1)设登山组人数为x人,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,
则有=47.5%,=10%,
解得b=50%,c=10%.
故a=100%﹣50%﹣10%=40%,
即游泳组中,青年人、中年人、老年人各占比例分别为40%、50%、10%.
(2)游泳组中,抽取的青年人数为200××40%=60(人);
抽取的中年人数为200××50%=75(人);
抽取的老年人数为200××10%=15(人).
(3)∵游泳组中,青年人、中年人、老年人分别抽取的人数为:60,75,15人;
∴职工的平均满意度的估计值为:×100%=79%,
∴估计游泳组中的职工的平均满意度为79%.
21.开学以来30天内的课外作业时间,学校采用分层抽样方法,从中抽取了100名学生进行问卷调查.将样本中的“小学生”和“初中学生”按学生的课外作业时间(单位:小时)各分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],得其频率分布直方图如图所示.
(Ⅰ)试估计全校学生中课外作业时间在[30,40)内的总人数;
(Ⅱ)从课外作业时间不足10个小时的样本学生中随机抽取3人,求至少有两个小学生的概率;
(Ⅲ)国家规定:小学生(3~6年级)平均每人每天课外作业时间不超过1小时.若该校小学生课外作业时间大于国家标准,则学校应适当减少课外作业时间.试根据以上抽样调查数据,判断该校小学生(3~6年级)是否需要减少课外作业时间.(同一组中的数据用该组区间的中点值作代表)
解:(I)小学生中,课外作业时间在[30,40)小时内的频率为1﹣(0.003+0.005+0.03+0.04)×10=0.22;
∴所有的小学生中,课外作业时间在[30,40)小时内的学生约有0.22×1800=396人;
初中生中,课外作业时间在[30,40)小时内的频率为1﹣(0.005+0.025+0.035+0.005)×10=0.30,
∴所有的初中生中,课外作业时间在[30,40)小时内的学生约有0.30×1200=360人;
则该校所有学生中,课外作业时间在[30,40)小时内的学生人数约有396+360=756人.
(II)记“从课外作业时间不足10个小时的样本学生中随机抽取3人,至少抽到2名小学生”为事件A.
由分层抽样知,抽取的小学生有名,初中生有100﹣60=40名.
小学生中,课外作业时间不足10个小时的学生频率为0.005×10=0.05,则样本人数为0.05×60=3人;
初中生中,课外作业时间不足10个小时的学生频率为0.005×10=0.05,样本人数为0.05×40=2人.
记这3名小学生为A,B,C,这2名初中生为d,e,
则从课外作业时间不足10个小时的样本学生中随机抽取3人,所有可能结果为:ABC,ABd,ABe,ACd,ACe,Ade,BCd,BCe,Bde,Cde,共10种;
其中事件A的结果为:ABC,ABd,ABe,ACd,ACe,BCd,BCe,共7种;
∴至少抽到2名小学生的概率为.
(III)小学生平均每人课外作业时间(小时)为:5×0.05+15×0.3+25×0.4+35×0.22+45×0.03=23.8,30×1=30.
∵23.8<30,
∴该校不需要减少小学生课外作业时间.
22.随着手机和网络的普及,外卖行业得到迅速的发展.某外卖平台为了解某地区用户对其提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:
用户编号 评分 用户编号 评分 用户编号 评分 用户编号 评分
1 78 11 88 21 79 31 93
2 73 12 86 22 83 32 78
3 81 13 95 23 72 33 75
4 92 14 76 24 74 34 81
5 95 15 97 25 91 35 84
6 85 16 78 26 66 36 77
7 79 17 88 27 80 37 81
8 84 18 82 28 83 38 76
9 63 19 76 29 74 39 85
10 86 20 89 30 82 40 89
(1)请你估计该地区所有用户评分的25%,95%分位数;
(2)若从这40个用户中抽取一个容量为10的样本,且抽到的10个用户的评分分别为92,84,86,78,89,74,83,78,77,89,试计算这10个数据的平均数和方差s2;
(3)在(2)的条件下,若用户的满意度评分在内,则满意度等级为“A级”,试用样本估计总体的思想,根据所抽到的10个数据,估计该地区满意度等级为“A级”的用户所占的百分比.
(参考数据:,,)
解:(1)这40个用户评分按从小到大排列如下:63,66,72,73,74,74,75,76,76,76,77,78,78,78,79,79,80,81,81,81,82,82,83,83,84,84,85,85,86,86,88,88,89,89,91,92,93,95,95,97,
得到,,
可知这40个用户评分的25%,95%分位数分别为第10项和第11项数据的平均数,第38项和第39项数据的平均数,分别为76.5,95,
据此估计该地区所有用户评分的25%,95%分位数分别约为76.5,95.
(2)=83,+(83﹣83)2+(78﹣83)2+(77﹣83)2+(89﹣83)2]=33.
(3)由题意知评分在,即(77.26,88.74)内的满意度等级为“A级”,样本中评分在(77.26,88.74)内的有5人,则可估计该地区满意度等级为“A级”的用户所占的百分比约为.
第九章 统计 章末综合测试
必修第二册高中数学人教A版(2019)
考试范围:必修第二册第九章 统计;考试满分:150分
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
第Ⅰ卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某学校想了解高一学生社会实践项目的选择意向,采用分层抽样的方式抽取100人进行问卷调查.已知高一年级有270名男生,从男生中抽取了60名,则该校高一年级共有学生( )
A.445人 B.450人 C.520人 D.540人
2.从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出90户调查社会购买力的某一项指标,应采用的最佳抽样方法是( )
A.按家庭分层抽样 B.按收入分层抽样
C.简单随机抽样 D.各种方法均可
3.要考察某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,…499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则第四袋牛奶的标号是( )
(下面摘取了某随机数表的第7行至第9行)
84421 75531 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98301 07185 12867 35807 44395 23879 33211
A.358 B.301 C.071 D.206
4.某日某火锅店进货了四种食品,其中毛肚、鸭肠、牛肉及莴笋分别进货了700份、600份、500份、200份,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的毛肚份数与莴笋份数之和是( )
A.7 B.13 C.8 D.9
5.某单位为了解该单位党员开展学习党史知识活动情况,随机抽取了部分党员,对他们一周的党史学习时间进行了统计,统计数据如下表所示:
党史学习时间(小时) 7 8 9 10 11
党员人数 6 10 9 7 8
则该单位党员一周学习党史时间的众数及第50百分位数分别是( )
A.8,8.5 B.8,8 C.9,8 D.8,9
6.已知数据x1,x2,…xn是某市n(n≥3,n∈N*)个普通职工的年收入,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是( )
A.年收入的平均数可能不变,中位数可能不变,方差可能不变
B.年收入的平均数大大增加,中位数可能不变,方差变大
C.年收入的平均数大大增加,中位数可能不变,方差也不变
D.年收入的平均数大大增加,中位数一定变大,方差可能不变
7.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图(如图),则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980﹣1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事产品岗位的90后人数超过总人数的5%
D.互联网行业中从事运营岗位的90后人数比80前从事互联网行业的人数多
8.已知一组数据x1,x2, ,xn的平均数为,标准差为s.若3x1﹣2,3x2﹣2, ,3xn﹣2的平均数与方差相等,则的最大值为( )
A. B. C. D.﹣2
第Ⅱ卷(非选择题)
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知数据x1,x2,x3,…,xn的众数、平均数、方差、第80百分位数分别是a1,b1,c1,d1,数据y1,y2,y3,…,yn的众数、平均数、方差、第80百分位数分别是a2,b2,c2,d2,且满足yi=3xi﹣1(i=1,2,3, ,n),则下列结论正确的是( )
A.b2=3b1﹣1 B.a2=a1 C.c2=9c1 D.d2=3d1﹣1
10.为推动学校体育运动发展,引导学生积极参与体育锻炼,增强健康管理意识,某校根据性别比例采用分层抽样方法随机抽取了120名男生和80名女生,调查并分别绘制出男、女生每天在校平均体育活动时间的频率分布直方图(如图所示),则( )
A.a=0.010
B.该校男生每天在校平均体育活动时间中位数的估计值为75
C.估计该校至少有一半学生每天在校平均体育活动时间超过一小时
D.估计该校每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为3:1
11.四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的有( )
A.中位数为3,众数为3 B.平均数为3,众数为4
C.平均数为3,中位数为3 D.平均数为2,方差为2.4
12.关于用统计方法获取数据,分析数据,下列结论正确的是( )
A.某食品加工企业为了解生产的产品是否合格,合理的调查方式为抽样调查
B.为了解高一学生的视力情况,现有高一男生480人,女生420人,按性别进行分层抽样,样本量按比例分配,若从女生中抽取的样本量为63,则样本容量为135
C.若甲、乙两组数据的标准差满足s甲<s乙,则可以估计乙比甲更稳定
D.若数据x1,x2,x3,…,xn的平均数为,则数据yi=axi﹣b(i=1,2,3,…,n)的平均数为a﹣b
三、填空题:本题共4小题,每小题5分,共20分。
13.若一组数据a1,a2,a3,…,an的方差为4,则3a1﹣1,3a2﹣1,3a3﹣1,…,3an﹣1的标准差为 .
14.用样本估计总体的统计思想在我国古代数学名著《数书九章》中就有记载,其中有道“米谷粒分”题:粮仓开仓收粮,有人送来米1600石,验得米内夹谷,抽样取米一把,数得250粒内夹谷25粒,估计这批米内所夹的谷有 石.
15.某校抽取100名学生测身高,其中身高最大值为186cm,最小值为154cm,根据身高数据绘制频率组距分布直方图,组距为5,且第一组下限为153.5,则组数为 .
16.由8个整数形成的样本数据中,至少有六个互不相同的整数,若平均数、中位数、唯一的众数和全距(即样本中最大数与最小数之差)都是8,则可能成为样本数据中的最大整数是 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.立德中学高一年级某学生社团开展了“使用移动支付平台——支付宝与微信支付的对比分析”的课题研究.随机调查了1000名市民,结果显示:使用支付宝的有456人,使用微信支付的有783人,两种都使用的有298人.
(1)只使用支付宝不使用微信支付的有多少人?
(2)两种移动支付方式都不使用的有多少人?(要有合理的说明过程)
18.某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛的得分情况如下:
甲:15,17,14,23,22,24,32;
乙:12,13,11,23,27,31,30.
(1)分别计算甲、乙两名运动员得分的平均数;
(2)分别计算甲、乙两名运动员得分的方差,并判断哪位运动员的成绩更稳定?
19.某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,得到体育成绩的折线图如图所示.
(1)若体育成绩大于或等于70分的学生为“体育良生”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良生”的人数;
(2)用样本估计总体的思想,试估计该校高一年级学生达标测试的平均分;
(3)假设甲、乙、丙三人的体育成绩分别为a、b、c,且a∈[70,80),b∈[80,90),c∈[90,100],当三人的体育成绩方差s2最小时,写出a、b、c的所有可能取值.(不要求证明)
20.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.
(1)试求游泳组中,青年人、中年人、老年人分别所占的比例;
(2)试求游泳组中,青年人、中年人、老年人分别应抽取的人数;
(3)如果游泳组中抽取的样本经调查得知青年人的平均满意度为75%,中年人的平均满意度为80%,老年人的平均满意度为90%,试估计游泳组中的职工的平均满意度.
21.开学以来30天内的课外作业时间,学校采用分层抽样方法,从中抽取了100名学生进行问卷调查.将样本中的“小学生”和“初中学生”按学生的课外作业时间(单位:小时)各分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],得其频率分布直方图如图所示.
(Ⅰ)试估计全校学生中课外作业时间在[30,40)内的总人数;
(Ⅱ)从课外作业时间不足10个小时的样本学生中随机抽取3人,求至少有两个小学生的概率;
(Ⅲ)国家规定:小学生(3~6年级)平均每人每天课外作业时间不超过1小时.若该校小学生课外作业时间大于国家标准,则学校应适当减少课外作业时间.试根据以上抽样调查数据,判断该校小学生(3~6年级)是否需要减少课外作业时间.(同一组中的数据用该组区间的中点值作代表)
22.随着手机和网络的普及,外卖行业得到迅速的发展.某外卖平台为了解某地区用户对其提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:
用户编号 评分 用户编号 评分 用户编号 评分 用户编号 评分
1 78 11 88 21 79 31 93
2 73 12 86 22 83 32 78
3 81 13 95 23 72 33 75
4 92 14 76 24 74 34 81
5 95 15 97 25 91 35 84
6 85 16 78 26 66 36 77
7 79 17 88 27 80 37 81
8 84 18 82 28 83 38 76
9 63 19 76 29 74 39 85
10 86 20 89 30 82 40 89
(1)请你估计该地区所有用户评分的25%,95%分位数;
(2)若从这40个用户中抽取一个容量为10的样本,且抽到的10个用户的评分分别为92,84,86,78,89,74,83,78,77,89,试计算这10个数据的平均数和方差s2;
(3)在(2)的条件下,若用户的满意度评分在内,则满意度等级为“A级”,试用样本估计总体的思想,根据所抽到的10个数据,估计该地区满意度等级为“A级”的用户所占的百分比.
(参考数据:,,)
第九章 统计 章末综合测试
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某学校想了解高一学生社会实践项目的选择意向,采用分层抽样的方式抽取100人进行问卷调查.已知高一年级有270名男生,从男生中抽取了60名,则该校高一年级共有学生( )
A.445人 B.450人 C.520人 D.540人
解:由题意计算抽样比例为=,
所以该校高一年级共有学生270×=450(人).
故选:B.
2.从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出90户调查社会购买力的某一项指标,应采用的最佳抽样方法是( )
A.按家庭分层抽样 B.按收入分层抽样
C.简单随机抽样 D.各种方法均可
解:因为社会购买力的某项指标受到家庭收入的影响,
而社区中各个家庭收入差别明显,
故应采用的最佳抽样方法是分层抽样.
故选:B.
3.要考察某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,…499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则第四袋牛奶的标号是( )
(下面摘取了某随机数表的第7行至第9行)
84421 75531 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98301 07185 12867 35807 44395 23879 33211
A.358 B.301 C.071 D.206
解:由题意可知,读取的第一个数据是583,不符合条件,第二个数据是921,不符合条件,第三个数据是206,符合条件,
即随机选取的第一袋牛奶标号是206,
以下数据依次是766,301,647,859,169,555,671,998,301,其中符合题意的数据只有301,169,301三个数据,但是301属于重复数据,继续往后计数,下一个数是071,符合条件,即前四袋牛奶的标号依次为206,301,169,071,
所以第四袋牛奶的标号为071.
故选:C.
4.某日某火锅店进货了四种食品,其中毛肚、鸭肠、牛肉及莴笋分别进货了700份、600份、500份、200份,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的毛肚份数与莴笋份数之和是( )
A.7 B.13 C.8 D.9
解:由题意,抽样的比例为=,
则应抽取的毛肚份数与莴笋份数之和为(700+200)×=9,
故选:D.
5.某单位为了解该单位党员开展学习党史知识活动情况,随机抽取了部分党员,对他们一周的党史学习时间进行了统计,统计数据如下表所示:
党史学习时间(小时) 7 8 9 10 11
党员人数 6 10 9 7 8
则该单位党员一周学习党史时间的众数及第50百分位数分别是( )
A.8,8.5 B.8,8 C.9,8 D.8,9
解:由图表可知众数为8,
共6+10+9+7+8=40人,
40×50%=20,
所以第50百分位数为9.
故选:D.
6.已知数据x1,x2,…xn是某市n(n≥3,n∈N*)个普通职工的年收入,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是( )
A.年收入的平均数可能不变,中位数可能不变,方差可能不变
B.年收入的平均数大大增加,中位数可能不变,方差变大
C.年收入的平均数大大增加,中位数可能不变,方差也不变
D.年收入的平均数大大增加,中位数一定变大,方差可能不变
解:因为数据x1,x2,x3,…,xn是普通职工n(n≥3,n∈N*)个人的年收入,
而xn+1为世界首富的年收入
则xn+1会远大于x1,x2,x3,…,xn,
故这n+1个数据中,年收入平均数大大增大,中位数可能不变,也可能稍微变大,
由于数据的集中程度也受到xn+1比较大的影响,而更加离散,则方差变大.
故选:B.
7.某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图(如图),则下列结论中不正确的是( )
注:90后指1990年及以后出生,80后指1980﹣1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事产品岗位的90后人数超过总人数的5%
D.互联网行业中从事运营岗位的90后人数比80前从事互联网行业的人数多
解:由整个互联网行业从业者年龄分布饼状图知,
互联网行业从业人员中90后占56%,
故选项A不符合题意;
∵56%×39.6%≈22.17%,
∴互联网行业中从事技术岗位的人数超过总人数的20%,
故选项B不符合题意;
∵56%×6.5%=3.64%,
∴互联网行业中从事产品岗位的90后人数不到总人数的5%,
故选项C符合题意;
∵56%×17%=9.52%,
∴互联网行业中从事运营岗位的90后人数占总人数的9.52%,
而80前从事互联网行业的人数占总人数的3%,
故互联网行业中从事运营岗位的90后人数比80前从事互联网行业的人数多,
故选项D不符合题意.
故选:C.
8.已知一组数据x1,x2, ,xn的平均数为,标准差为s.若3x1﹣2,3x2﹣2, ,3xn﹣2的平均数与方差相等,则的最大值为( )
A. B. C. D.﹣2
解:由题意可得3﹣2=9s2,则s=.因为s2≥0,所以3﹣2≥0,解得.
令y=s﹣=﹣().
设t=,则=(t≥0),
从而=≤﹣,故.
故选:A.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知数据x1,x2,x3,…,xn的众数、平均数、方差、第80百分位数分别是a1,b1,c1,d1,数据y1,y2,y3,…,yn的众数、平均数、方差、第80百分位数分别是a2,b2,c2,d2,且满足yi=3xi﹣1(i=1,2,3, ,n),则下列结论正确的是( )
A.b2=3b1﹣1 B.a2=a1 C.c2=9c1 D.d2=3d1﹣1
解:由题意可知,两组数据满足yi=3xi﹣1(i=1,2,3, ,n),
由平均数计算公式得×(y1+y2+...+yn)=×[(3x1﹣1)+(3x2﹣1)+…+(3xn﹣1)]=3××(x1+x2+…+xn)﹣1,
所以b2=3b1﹣1,故A正确;
由它们的众数也满足yi=3xi﹣1(i=1,2,3, ,n),
则有a2=3a1﹣1,故B错误;
由方差的性质得c2=9c1,故C正确;
对于数据x1,x2,x3,…,xn,假设其第80百分位数为d1,
当0.8n=k是整数时,d1=,
当0.8n不是整数时,设其整数部分为k,则d1=xk+1,
所以对于数据3x1﹣1,3x2﹣1,3x3﹣1,…,3xn﹣1,假设其第80百分位数为d2,
当0.8n=k是整数时,d2==3d1﹣1,
当0.8n不是整数时,设其整数部分为k,则d2=3xk+1﹣1=3d1﹣1,
所以d2=3d1﹣1,故D正确.
故选:ACD.
10.为推动学校体育运动发展,引导学生积极参与体育锻炼,增强健康管理意识,某校根据性别比例采用分层抽样方法随机抽取了120名男生和80名女生,调查并分别绘制出男、女生每天在校平均体育活动时间的频率分布直方图(如图所示),则( )
A.a=0.010
B.该校男生每天在校平均体育活动时间中位数的估计值为75
C.估计该校至少有一半学生每天在校平均体育活动时间超过一小时
D.估计该校每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为3:1
解:对于A,10a+10×0.020+10×0.035+10×0.020+10a+10×0.005=1,解得,a=0.010,
对于B,a=0.010,前两个小矩形面积之和为0.3,即中位数在[60,70)内,设为m,
则,解得,
该校男生每天在校平均体育活动时间中位数的估计值为65.7,
对于C,根据频率分布直方图可得,男生中每天在校平均体育活动时间超过一小时的频率为10×(0.035+0.020+0.010+0.005)=0.700,
人数为120×0.7=84,
女生中每天在校平均体育活动时间超过一小时的频率为10×(0.030+0.010+0.005)=0.450,人数为80×0.450=36,
故学生每天在校平均体育活动时间超过一小时的频率为,
故该校至少有一半学生每天在校平均体育活动时间超过一小时,
对于D,男生中每天在校平均体育活动时间不低于80分钟的频率为10×(0.010+0.005)=0.15,人数为120×0.15=18,
女生中每天在校平均体育活动时间不低于80分钟的频率为10×0.005=0.050,人数为80×0.050=4,
所以每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为,
所以该校每天在校平均体育活动时间不低于80分钟的学生中男、女生人数比例为9:2.
故选:AC.
11.四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的有( )
A.中位数为3,众数为3 B.平均数为3,众数为4
C.平均数为3,中位数为3 D.平均数为2,方差为2.4
解:对于A,当掷骰子出现的结果为1,2,3,3,6时,
满足中位数为3,众数为3,所以A不可以判断;
对于B,若平均数为3,且出现点数为6,则其余4个数的和为9,
而众数为4,故其余4个数的和至少为10,所以B可以判断;
对于C,当掷骰子出现的结果为1,1,3,4,6时,
满足平均数为3,中位数为3,可以出现点6,所以C不能判断;
对于D,若平均数为2,且出现点数6,
则方差S2>(6﹣2)2=3.2>2.4,
所以当平均数为2,方差为2.4时,一定不会出现点数6.
故选:BD.
12.关于用统计方法获取数据,分析数据,下列结论正确的是( )
A.某食品加工企业为了解生产的产品是否合格,合理的调查方式为抽样调查
B.为了解高一学生的视力情况,现有高一男生480人,女生420人,按性别进行分层抽样,样本量按比例分配,若从女生中抽取的样本量为63,则样本容量为135
C.若甲、乙两组数据的标准差满足s甲<s乙,则可以估计乙比甲更稳定
D.若数据x1,x2,x3,…,xn的平均数为,则数据yi=axi﹣b(i=1,2,3,…,n)的平均数为a﹣b
解:对于A,了解生产的产品是否合格,合理的调查 方式为抽样调查,故A正确;
对于B,根据分层抽样抽样比可知样本容量为×(480+420)=135,故B正确;
对于C,∵S甲<S乙,∴甲的数据更稳定,故C错误;
对于D,根据平均数的性质,yi=axi﹣b(i=1,2,3, ,n)的平均数为﹣b,故D正确.
故选:ABD.
三、填空题:本题共4小题,每小题5分,共20分。
13.若一组数据a1,a2,a3,…,an的方差为4,则3a1﹣1,3a2﹣1,3a3﹣1,…,3an﹣1的标准差为 6 .
解:因为a1,a2,a3,…,an的方差为4,
所以3a1﹣1,3a2﹣1,3a3﹣1,…,3an﹣1的方差为32×4=36,
所以3a1﹣1,3a2﹣1,3a3﹣1,…,3an﹣1的标准差为6.
故答案为:6.
14.用样本估计总体的统计思想在我国古代数学名著《数书九章》中就有记载,其中有道“米谷粒分”题:粮仓开仓收粮,有人送来米1600石,验得米内夹谷,抽样取米一把,数得250粒内夹谷25粒,估计这批米内所夹的谷有 160 石.
解:依题意,设这批米内所夹的谷有x石,
则,解得x=160,
所以估计这批米内所夹的谷有160石.
故答案为:160.
15.某校抽取100名学生测身高,其中身高最大值为186cm,最小值为154cm,根据身高数据绘制频率组距分布直方图,组距为5,且第一组下限为153.5,则组数为 7 .
解:极差为186﹣154=32,组距为5,且第一组下限为153.5,
=6.4,故组数为7组,
故答案为:7.
16.由8个整数形成的样本数据中,至少有六个互不相同的整数,若平均数、中位数、唯一的众数和全距(即样本中最大数与最小数之差)都是8,则可能成为样本数据中的最大整数是 12 .
解:依题意,平均数=中位数=众数=8,所以偏态系数为0,数据分布对称,
因为存在众数且众数唯一,
所以可设这8个整数为x1,x2,x3,8,8,x4,x5,x6,
且x1<x2<x3<8=8<x4<x5<x6,
所以,解得x6=12.
故答案为:12.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.立德中学高一年级某学生社团开展了“使用移动支付平台——支付宝与微信支付的对比分析”的课题研究.随机调查了1000名市民,结果显示:使用支付宝的有456人,使用微信支付的有783人,两种都使用的有298人.
(1)只使用支付宝不使用微信支付的有多少人?
(2)两种移动支付方式都不使用的有多少人?(要有合理的说明过程)
解:(1)因为“使用支付宝”的有456人,“两种支付方式都使用”的有298人,
所以“只使用支付宝不使用微信支付”的有456﹣298=158(人).
(2)同(1)有,“只使用微信支付不使用支付宝”的有783﹣298=485(人),
所以,“至少使用一种移动支付方式”的有485+158+298=941(人),
故“两种移动支付方式都不使用”有1000﹣941=59(人).
18.某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛的得分情况如下:
甲:15,17,14,23,22,24,32;
乙:12,13,11,23,27,31,30.
(1)分别计算甲、乙两名运动员得分的平均数;
(2)分别计算甲、乙两名运动员得分的方差,并判断哪位运动员的成绩更稳定?
解:(1)设甲、乙的平均分别记为,,
则,,
故甲、乙两名运动员得分的平均数均为21;
(2)设甲、乙两名运动员得分的方差分别为,
则=,=,
∵,
∴甲运动员的成绩更稳定.
19.某校高一年级学生全部参加了体育科目的达标测试,现从中随机抽取40名学生的测试成绩,整理数据并按分数段[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]进行分组.已知测试分数均为整数,现用每组区间的中点值代替该组中的每个数据,得到体育成绩的折线图如图所示.
(1)若体育成绩大于或等于70分的学生为“体育良生”,已知该校高一年级有1000名学生,试估计该校高一年级学生“体育良生”的人数;
(2)用样本估计总体的思想,试估计该校高一年级学生达标测试的平均分;
(3)假设甲、乙、丙三人的体育成绩分别为a、b、c,且a∈[70,80),b∈[80,90),c∈[90,100],当三人的体育成绩方差s2最小时,写出a、b、c的所有可能取值.(不要求证明)
解:(1)根据折线图体育成绩大于或等于70分的学生有14+3+13=30(人),
所以该校高一年级学生“体育良生”的人数为(人).
(2)用样本估计总体的思想,估计该校高一年级学生达标测试的平均分为.
(3)由于甲、乙、丙三人的体育成绩分别为a,b,c,且a∈[70,80),b∈[80,90),其中a,b,c∈N,当三人的体育成绩方差s2最小时,a、b、c的所有可能取值79.84,90或79,85,90.
20.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的,且该组中青年人占50%,中年人占40%,老年人占10%.为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.
(1)试求游泳组中,青年人、中年人、老年人分别所占的比例;
(2)试求游泳组中,青年人、中年人、老年人分别应抽取的人数;
(3)如果游泳组中抽取的样本经调查得知青年人的平均满意度为75%,中年人的平均满意度为80%,老年人的平均满意度为90%,试估计游泳组中的职工的平均满意度.
解:(1)设登山组人数为x人,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,
则有=47.5%,=10%,
解得b=50%,c=10%.
故a=100%﹣50%﹣10%=40%,
即游泳组中,青年人、中年人、老年人各占比例分别为40%、50%、10%.
(2)游泳组中,抽取的青年人数为200××40%=60(人);
抽取的中年人数为200××50%=75(人);
抽取的老年人数为200××10%=15(人).
(3)∵游泳组中,青年人、中年人、老年人分别抽取的人数为:60,75,15人;
∴职工的平均满意度的估计值为:×100%=79%,
∴估计游泳组中的职工的平均满意度为79%.
21.开学以来30天内的课外作业时间,学校采用分层抽样方法,从中抽取了100名学生进行问卷调查.将样本中的“小学生”和“初中学生”按学生的课外作业时间(单位:小时)各分为5组:[0,10),[10,20),[20,30),[30,40),[40,50],得其频率分布直方图如图所示.
(Ⅰ)试估计全校学生中课外作业时间在[30,40)内的总人数;
(Ⅱ)从课外作业时间不足10个小时的样本学生中随机抽取3人,求至少有两个小学生的概率;
(Ⅲ)国家规定:小学生(3~6年级)平均每人每天课外作业时间不超过1小时.若该校小学生课外作业时间大于国家标准,则学校应适当减少课外作业时间.试根据以上抽样调查数据,判断该校小学生(3~6年级)是否需要减少课外作业时间.(同一组中的数据用该组区间的中点值作代表)
解:(I)小学生中,课外作业时间在[30,40)小时内的频率为1﹣(0.003+0.005+0.03+0.04)×10=0.22;
∴所有的小学生中,课外作业时间在[30,40)小时内的学生约有0.22×1800=396人;
初中生中,课外作业时间在[30,40)小时内的频率为1﹣(0.005+0.025+0.035+0.005)×10=0.30,
∴所有的初中生中,课外作业时间在[30,40)小时内的学生约有0.30×1200=360人;
则该校所有学生中,课外作业时间在[30,40)小时内的学生人数约有396+360=756人.
(II)记“从课外作业时间不足10个小时的样本学生中随机抽取3人,至少抽到2名小学生”为事件A.
由分层抽样知,抽取的小学生有名,初中生有100﹣60=40名.
小学生中,课外作业时间不足10个小时的学生频率为0.005×10=0.05,则样本人数为0.05×60=3人;
初中生中,课外作业时间不足10个小时的学生频率为0.005×10=0.05,样本人数为0.05×40=2人.
记这3名小学生为A,B,C,这2名初中生为d,e,
则从课外作业时间不足10个小时的样本学生中随机抽取3人,所有可能结果为:ABC,ABd,ABe,ACd,ACe,Ade,BCd,BCe,Bde,Cde,共10种;
其中事件A的结果为:ABC,ABd,ABe,ACd,ACe,BCd,BCe,共7种;
∴至少抽到2名小学生的概率为.
(III)小学生平均每人课外作业时间(小时)为:5×0.05+15×0.3+25×0.4+35×0.22+45×0.03=23.8,30×1=30.
∵23.8<30,
∴该校不需要减少小学生课外作业时间.
22.随着手机和网络的普及,外卖行业得到迅速的发展.某外卖平台为了解某地区用户对其提供的服务的满意度,随机调查了40个用户,得到用户的满意度评分如下:
用户编号 评分 用户编号 评分 用户编号 评分 用户编号 评分
1 78 11 88 21 79 31 93
2 73 12 86 22 83 32 78
3 81 13 95 23 72 33 75
4 92 14 76 24 74 34 81
5 95 15 97 25 91 35 84
6 85 16 78 26 66 36 77
7 79 17 88 27 80 37 81
8 84 18 82 28 83 38 76
9 63 19 76 29 74 39 85
10 86 20 89 30 82 40 89
(1)请你估计该地区所有用户评分的25%,95%分位数;
(2)若从这40个用户中抽取一个容量为10的样本,且抽到的10个用户的评分分别为92,84,86,78,89,74,83,78,77,89,试计算这10个数据的平均数和方差s2;
(3)在(2)的条件下,若用户的满意度评分在内,则满意度等级为“A级”,试用样本估计总体的思想,根据所抽到的10个数据,估计该地区满意度等级为“A级”的用户所占的百分比.
(参考数据:,,)
解:(1)这40个用户评分按从小到大排列如下:63,66,72,73,74,74,75,76,76,76,77,78,78,78,79,79,80,81,81,81,82,82,83,83,84,84,85,85,86,86,88,88,89,89,91,92,93,95,95,97,
得到,,
可知这40个用户评分的25%,95%分位数分别为第10项和第11项数据的平均数,第38项和第39项数据的平均数,分别为76.5,95,
据此估计该地区所有用户评分的25%,95%分位数分别约为76.5,95.
(2)=83,+(83﹣83)2+(78﹣83)2+(77﹣83)2+(89﹣83)2]=33.
(3)由题意知评分在,即(77.26,88.74)内的满意度等级为“A级”,样本中评分在(77.26,88.74)内的有5人,则可估计该地区满意度等级为“A级”的用户所占的百分比约为.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
