第5章一元函数的导数及其应用 章末综合测试 -2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册(含解析)
文档属性
| 名称 | 第5章一元函数的导数及其应用 章末综合测试 -2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 356.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 05:08:03 | ||
图片预览

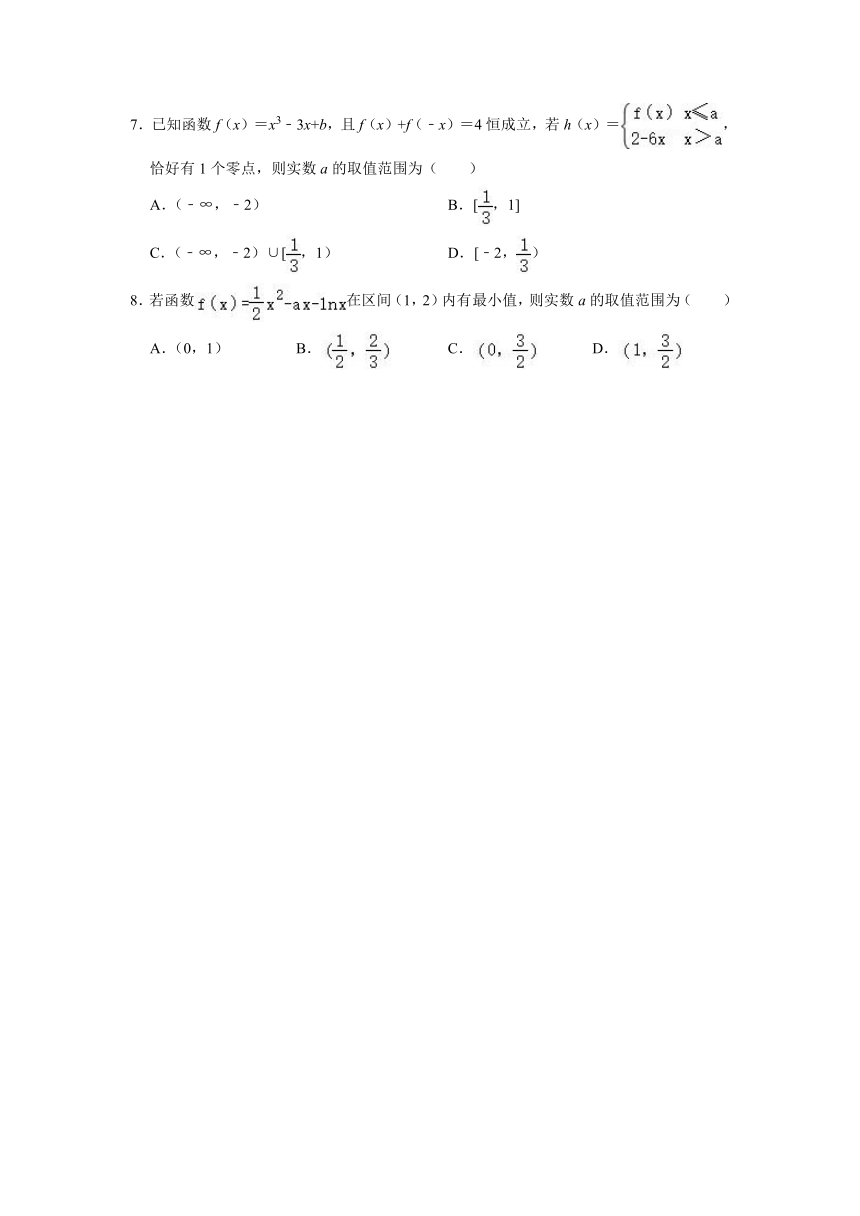



文档简介
绝密★启用前
第5章 一元函数的导数及其应用 章末综合测试
选择性必修第二册高中数学人教A版【2019】
考试范围:第5章一元函数的导数及其应用;试卷满分:150分
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
第Ⅰ卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知f(x)是定义在R上的可导函数,若,则f′(2)=( )
A.﹣1 B. C.1 D.
2.曲线f(x)=ex+x2﹣2x﹣5在x=0处的切线的倾斜角是( )
A. B. C. D.
3.已知函数f(x)的导函数为f'(x),且,则=( )
A. B. C. D.
4.下列求导运算正确的是( )
A.(lnx)′=x B.
C.(cosx)′=sinx D.(ax)′=axlna(a>0,a≠1)
5.已知函数f(x)=x3+ax2+x+1(a∈R)有两个极值点x1,x2(x1<x2),则( )
A.或 B.x1是f(x)的极小值点
C.x1+x2= D.x1x2=﹣
6.设f(x)是定义在R上的函数,其导函数为f'(x),满足f(x)﹣xf'(x)>0,若a=4f(1),b=2f(2),c=f(4),则( )
A.a>b>c B.c>a>b C.b>c>a D.c>b>a
7.已知函数f(x)=x3﹣3x+b,且f(x)+f(﹣x)=4恒成立,若h(x)=,恰好有1个零点,则实数a的取值范围为( )
A.(﹣∞,﹣2) B.[,1]
C.(﹣∞,﹣2)∪[,1) D.[﹣2,)
8.若函数在区间(1,2)内有最小值,则实数a的取值范围为( )
A.(0,1) B. C. D.
第Ⅱ卷(非选择题)
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知定义在区间[a,b]上的函数y=f(x),f(x)是f(x)的导函数,若存在ξ∈(a,b),使得f(b)﹣f(a)=f′(ξ)(b﹣a).则称ξ为函数f(x)在[a,b]上的“中值点”.下列函数,其中在区间(﹣2,2]上至少有两个“中值点”的函数为( )
A.f(x)=sinx B.f(x)=ex
C.f(x)=ln(x+3) D.f(x)=x3﹣x+1
10.已知x2﹣y2<ex﹣e﹣y,则( )
A.ln(x+y+1)<0 B.(x+y)2+1<ex+y
C.x+y>﹣sinx﹣siny D.cosx﹣cosy>y2﹣x2
11.已知函数f(x)=ln(x+2)+ln(4﹣x),则下列说法正确的是( )
A.f(x)在区间(﹣2,1)上单调递增
B.f(x)在区间(1,+∞)上单调递减
C.f(x)在图象关于直线x=1对称
D.f(x)的图象关于点(1,0)对称
12.已知函数f(x)及其导函数f′(x)的定义域均为R,记g(x)=f′(x),f(2x﹣1)+f(3﹣2x)=f(﹣2),g(﹣1+3x)+g(﹣3x)=g,则( )
A.f(4)=0 B.g(2)=g(﹣1)
C.g()=0 D.g(2022)=g(0)
三、填空题:本题共4小题,每小题5分,共20分。
13.如图,直线l是曲线y=f(x)在点(4,f(4))处的切线,则f(4)+f′(4)的值等于 .
14.已知函数f(x)=ex﹣1﹣alnx﹣a,若曲线y=f(x)在点(1,f(1))处的切线与直线2x+y﹣1=0垂直,则切线的方程为 .
15.已知函数f(x)及其导函数f'(x)的定义域均为R,f(x)为奇函数,且f(x)﹣f'(x)>0.则不等式f(x2﹣3x+2)>0的解集为 .
16.已知不等式e2x﹣kx2+x≥lnx+lnk(k>0)恒成立,则k的最大值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.求下列函数的导数.
①;②y=(2x2﹣1)(3x+1);
③;④.
18.已知函数f(x)=exsinx﹣x+1.
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)求函数f(x)在区间上的最大值和最小值.
19.设函数,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0.
(1)求y=f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
20.已知函数f(x)=x3+ax2+x(a∈R).
(1)若函数f(x)存在两个极值点,求a的取值范围;
(2)若f(x)≥xlnx+x在(0,+∞)恒成立,求a的最小值.
21.已知函数f(x)=.
(1)若f(x)在(0,e2]上单调递增,求实数a的取值范围;
(2)若f(x)≤xex+﹣1恒成立,求实数a的取值范围.
22.已知函数f(x)=alnx﹣bx,其中a,b∈R.
(1)若a=1,求函数f(x)的单调区间;
(2)若b=1,函数f(x)有两个相异的零点x1,x2,求证:x1x2>e2.
第5章 一元函数的导数及其应用 章末综合测试
参考答案与试题解析
一.选择题(共8小题)
1.已知f(x)是定义在R上的可导函数,若,则f′(2)=( )
A.﹣1 B. C.1 D.
解:.
故选:A.
2.曲线f(x)=ex+x2﹣2x﹣5在x=0处的切线的倾斜角是( )
A. B. C. D.
解:曲线f(x)=ex+x2﹣2x﹣5,∴f′(x)=ex+2x﹣2,
故f′(0)=﹣1,
即对应切线斜率为﹣1,故曲线f(x)=ex+x2﹣2x﹣5在x=0处的切线的倾斜角是.
故选:D.
3.已知函数f(x)的导函数为f'(x),且,则=( )
A. B. C. D.
解:,
∴,
∴,
∴f(x)=x+cosx,∴.
故选:D.
4.下列求导运算正确的是( )
A.(lnx)′=x B.
C.(cosx)′=sinx D.(ax)′=axlna(a>0,a≠1)
解:∵,A项错误;
∵是个常数,∴,∴B项错误;
∵(cosx)′=﹣sinx,∴C项错误;
∵(ax)′=axlna(a>0,a≠1),∴D项正确.
故选:D.
5.已知函数f(x)=x3+ax2+x+1(a∈R)有两个极值点x1,x2(x1<x2),则( )
A.或 B.x1是f(x)的极小值点
C.x1+x2= D.x1x2=﹣
解:若函数f(x)=x3+ax2+x+1(a∈R)有两个极值点x1,x2(x1<x2),
则f′(x)=3x2+2ax+1有2个不同零点,
则Δ=4a2﹣12>0,解得a>或a<﹣,故A正确,
由于3>0,则函数f′(x)的图像开口向上,
则x1是f(x)的极大值点,故B错误,
由x1 x2=,x1+x2=﹣,则CD错误,
故选:A.
6.设f(x)是定义在R上的函数,其导函数为f'(x),满足f(x)﹣xf'(x)>0,若a=4f(1),b=2f(2),c=f(4),则( )
A.a>b>c B.c>a>b C.b>c>a D.c>b>a
解:因为f(x)满足f(x)﹣xf′(x)<0,令,
则,所以g(x)在R上是增函数,
所以g(1)<g(2)<g(4),即,
所以c>b>a.
故选:D.
7.已知函数f(x)=x3﹣3x+b,且f(x)+f(﹣x)=4恒成立,若h(x)=,恰好有1个零点,则实数a的取值范围为( )
A.(﹣∞,﹣2) B.[,1]
C.(﹣∞,﹣2)∪[,1) D.[﹣2,)
解:因为f(x)+f(﹣x)=4恒成立,所以f(x)=x3﹣3x+b的图象关于点(0,2)对称,
所以b=2,且函数f(x)=x3﹣3x+2的零点为﹣2和1,y=2﹣6x的零点为,
在同一坐标系内分别画出函数f(x)=x3﹣3x+2与y=2﹣6x的图象,
当且仅当a<﹣2或时,函数恰好有1个零点,
因此实数a的取值范围为(﹣∞,﹣2)∪.
故选:C.
8.若函数在区间(1,2)内有最小值,则实数a的取值范围为( )
A.(0,1) B. C. D.
解:由,若函数f(x)在区间(1,2)内有最小值.此时函数f(x)必定存在极值点,
由Δ=a2+4>0,设x1,x2为一元二次方程x2﹣ax﹣1=0的两根,有,
故只需要1<x2<2即可,
令g(x)=x2﹣ax﹣1,有,解得.
故选:C.
二.多选题(共4小题)
9.已知定义在区间[a,b]上的函数y=f(x),f(x)是f(x)的导函数,若存在ξ∈(a,b),使得f(b)﹣f(a)=f′(ξ)(b﹣a).则称ξ为函数f(x)在[a,b]上的“中值点”.下列函数,其中在区间(﹣2,2]上至少有两个“中值点”的函数为( )
A.f(x)=sinx B.f(x)=ex
C.f(x)=ln(x+3) D.f(x)=x3﹣x+1
解:对于A选项,f(2)﹣f(﹣2)=2sin2,f′(x)=cosx,
由f(2)﹣f(﹣2)=4f′(ξ)=4cosξ,所以,cos=,
当ξ∈[﹣2,2]时,cos2≤cosξ≤1,如下图所示:
由图可知,直线y=与曲线y=cosξ在[﹣2,2]上的图象有两个交点,A选项满足条件;
对于B选项,f(2)﹣f(﹣2)=,f′(x)=ex,
由f(2)﹣f(﹣2)=4f′(ξ)=4eξ,所以,eξ=,
因为函数y=ex在[﹣2,2]上单调递增,故方程eξ=在[﹣2,2]上不可能有两个根,B不满足条件;
对于C选项,f(2)﹣f(﹣2)=ln5,f′(x)=,
由f(2)﹣f(﹣2)=4f′(ξ)=ln5,可得=,解得ξ=﹣3∈[﹣2,2],
故函数f(x)在[﹣2,2]上只有一个“中值点”,C选项不满足条件;
对于D选项,f′(x)=3x2﹣1,f(2)﹣f(﹣2)=12,
由f(2)﹣f(﹣2)=4f′(ξ)=12,可得ξ=∈[﹣2,2],
故函数f(x)在[﹣2,2]上有两个“中值点”,D满足条件.
故选:AD.
10.已知x2﹣y2<ex﹣e﹣y,则( )
A.ln(x+y+1)<0 B.(x+y)2+1<ex+y
C.x+y>﹣sinx﹣siny D.cosx﹣cosy>y2﹣x2
解:∵x2﹣y2<ex﹣e﹣y,即e﹣y﹣(﹣y)2<ex﹣x2,
对于A:令f(x)=ex﹣x2,f'(x)=ex﹣2x,f''(x)=ex﹣2,
由f''(x)=0得x=ln2,由f'(x)>0得x>ln2,由f'(x)<0得x<ln2,
∴f'(x)在(﹣∞,ln2)上单调递减,在(ln2,+∞)上单调递增,
∴当x=ln2时,f'(x)取得极小值也是最小值,f'(x)min=f'(ln2)=2﹣2ln2>0,
∴f(x)在R上单调递增,
∵e﹣y﹣(﹣y)2<ex﹣x2,即f(﹣y)<f(x),∴﹣y<x,即x+y>0,
∴x+y+1>1,则ln(x+y+1)>ln1=0,故A错误;
对于B:要证(x+y)2+1<ex+y,即证ex+y﹣(x+y)2﹣1>0,
令t=x+y,则et﹣t2﹣1>0,令g(t)=et﹣t2﹣1,
由选项A得f(x)=ex﹣x2在R上单调递增,则g(t)=et﹣t2﹣1在[0,+∞)上单调递增,
∴g(t)>g(0)=0,故B正确;
对于C:要证x+y>﹣sinx﹣siny,即证x+sinx>﹣y+sin(﹣y),
令f(x)=x+sinx,则f'(x)=1+cosx≥0,
∴f(x)在R上单调递增,
由选项A得﹣y<x,即f(﹣y)<f(x),即x+sinx>﹣y+sin(﹣y),故C正确;
对于D:要证cosx﹣cosy>y2﹣x2,即证cosx+x2>y2+cosy,
令f(x)=cosx+x2,则f'(x)=﹣sinx+2x,f''(x)=2﹣cosx>0,
∴f'(x)在R上单调递增,
由f'(x)=0得x=0,则当x>0时,f'(x)>0,当x<0时,f'(x)<0,
∴f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增,故无法判断f(﹣y)与f(x)的大小,故D错误,
故选:BC.
11.已知函数f(x)=ln(x+2)+ln(4﹣x),则下列说法正确的是( )
A.f(x)在区间(﹣2,1)上单调递增
B.f(x)在区间(1,+∞)上单调递减
C.f(x)在图象关于直线x=1对称
D.f(x)的图象关于点(1,0)对称
解:由题意得,解得﹣2<x<4,即函数f(x)的定义域为(﹣2,4),
f(x)=ln(x+2)+ln(4﹣x)=ln(x+2)(4﹣x)=ln(﹣x2+2x+8),
令t=﹣x2+2x+8=﹣(x﹣1)2+9,则t=﹣x2+2x+8在(﹣2,1)上单调递增,在(1,4)上单调递减,
∴f(x)在(﹣2,1)上单调递增,在(1,4)上单调递减,故A正确,B错误;
f(1﹣x)=ln(3﹣x)+ln(3+x),f(1+x)=ln(3+x)+ln(3﹣x),
∴f(1﹣x)=f(1+x),则f(x)在图象关于直线x=1对称,故C正确,D错误,
故选:AC.
12.已知函数f(x)及其导函数f′(x)的定义域均为R,记g(x)=f′(x),f(2x﹣1)+f(3﹣2x)=f(﹣2),g(﹣1+3x)+g(﹣3x)=g,则( )
A.f(4)=0 B.g(2)=g(﹣1)
C.g()=0 D.g(2022)=g(0)
解:因为f(2x﹣1)+f(3﹣2x)=f(﹣2),g(x)=f′(x),g(﹣1+3x)+g(﹣3x)=g,
令x=﹣,则f(﹣2)+f(4)=f(﹣2),解得f(4)=0,故A对;
令t=2x,故f(t﹣1)+f(3﹣t)=f(﹣2),两边对t求导,则f′(t﹣1)﹣f′(3﹣t)=0,即g(t﹣1)=g(3﹣t),所以g(t)关于t=1对称,
再令t=3x,则g(﹣1+t)+g(﹣t)=g(﹣),令t=得=0,故C正确;
所以g(﹣1+t)+g(﹣t)=0,又g(t﹣1)=g(3﹣t),令t=1得g(0)+g(﹣1)=0,g(0)=g(2),故g(2)=﹣g(﹣1),故B错;
再由g(﹣1+t)+g(﹣t)=0,且g(t﹣1)=g(3﹣t),得g(3﹣t)=﹣g(﹣t),故g(t)的周期T=6,故g(2022)=g(6×337)=g(0),故D正确.
故选:ACD.
三、填空题:本题共4小题,每小题5分,共20分。
13.如图,直线l是曲线y=f(x)在点(4,f(4))处的切线,则f(4)+f′(4)的值等于 .
解:由函数的图像可得f(4)=5,直线l过点(0,3)和(4,5),
则直线l的斜率,
又由直线l是曲线y=f(x)在点(4,f(4))处的切线,则,
所以.
故答案为:.
14.已知函数f(x)=ex﹣1﹣alnx﹣a,若曲线y=f(x)在点(1,f(1))处的切线与直线2x+y﹣1=0垂直,则切线的方程为 x﹣2y=0 .
解:由题可知f′(x)=ex﹣1 ,则f'(1)=1﹣a,
因为曲线y=f(x)在(1,f(1))处的切线与直线2x+y﹣1=0垂直,
所以1 a=,解得a=.
故f(x)=ex﹣1﹣lnx﹣,f(1)=1﹣=,
即切点为(1,),切线的斜率k=,
所以切线方程为:y﹣=(x﹣1),即x﹣2y=0.
故答案为:x﹣2y=0.
15.已知函数f(x)及其导函数f'(x)的定义域均为R,f(x)为奇函数,且f(x)﹣f'(x)>0.则不等式f(x2﹣3x+2)>0的解集为 (1,2) .
解:函数f(x)及其导函数f'(x)的定义域均为R,f(0)=0,令g(x)=,则g(0)=0,
则g'(x)=,
∵f(x)﹣f'(x)>0,∴g'(x)<0,即g(x)在R上单调递减,
不等式f(x2﹣3x+2)>0,即g(x2﹣3x+2)>g(0),
∴x2﹣3x+2<0,解得1<x<2,
∴不等式f(x2﹣3x+2)>0的解集为(1,2),
故答案为:(1,2).
16.已知不等式e2x﹣kx2+x≥lnx+lnk(k>0)恒成立,则k的最大值为 e2 .
解:不等式e2x﹣kx2+x≥lnx+lnk(k>0)恒成立,
等价于e2x+lne2x≥kx2+ln(kx2)(k>0)恒成立,
令f(x)=x+lnx(x>0),
则f′(x)=1+>0,f(x)=x+lnx在(0,+∞)上单调递增,
∴e2x≥kx2(k>0)恒成立,化为≤恒成立,
令g(x)=(x>0),则g′(x)=,
当x∈(0,1)时,g′(x)<0,x∈(1,+∞)时,g′(x)>0,
∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴g(x)的极小值,也是最小值为g(1)=e,
∴≤e,即k≤e2,
∴k的最大值为e2,
故答案为:e2.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.求下列函数的导数.
①;②y=(2x2﹣1)(3x+1);
③;④.
解:①.
②∵y=(2x2﹣1)(3x+1)=6x3+2x2﹣3x﹣1,
∴y'=(6x3+2x2﹣3x﹣1)′=18x2+4x﹣3.
③∵,
∴.
④.
18.已知函数f(x)=exsinx﹣x+1.
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)求函数f(x)在区间上的最大值和最小值.
解:(Ⅰ)因为f(x)=exsinx﹣x+1,
所以f'(x)=ex(cosx+sinx)﹣1,
又f(0)=1,f'(0)=0,
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
(Ⅱ)当,f′(x)=ex(sinx+cosx)﹣1,f″(x)=2ex cosx≥0,
所以y=f'(x)在区间上递增,
又f'(0)=0,
故当,f'(x)<f'(0)=0,
所以y=f(x)在上单减,
又当,f'(x)>f'(0)=0,
所以y=f(x)在上单增.
所以f(x)min=f(0)=1,.
19.设函数,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0.
(1)求y=f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
解析:(1)方程7x﹣4y﹣12=0可化为,当x=2时,,
又,于是,解得,故.
(2)设P(x0,y0)为曲线上任一点,由知曲线在点P(x0,y0)处的切线方程为,即
令x=0,得,从而得切线与直线x=0的交点坐标为;
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0);
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为.
故曲线y=f(x)上任一点处的切线与直线x=0,y=x所围成的三角形面积为定值,此定值为6.
20.已知函数f(x)=x3+ax2+x(a∈R).
(1)若函数f(x)存在两个极值点,求a的取值范围;
(2)若f(x)≥xlnx+x在(0,+∞)恒成立,求a的最小值.
解:(1)∵f(x)=x3+ax2+x(a∈R)存在两个极值点,
∴f′(x)=3x2+2ax+1=0有两个不同的零点,
∴4a2﹣12>0,解得或,即a的取值范围为(﹣∞,﹣)∪(,+∞);
(2)∵x3+ax2+x≥xlnx+x在(0,+∞)上恒成立,即x3+ax2≥xlnx在(0,+∞)上恒成立 a≥(﹣x)max,x>0.
令g(x)=﹣x(x>0),
则g′(x)=﹣1=(x>0),
令t(x)=﹣x2﹣lnx+1(x>0),
则t′(x)=﹣2x﹣<0,
∴t(x)在(0,+∞)上单调递减,
又t(1)=0,
∴当x∈(0,1)时,t′(x)>0,即g′(x)>0,g(x)在(0,1)上单调递增;
当x∈(1,+∞)时,t′(x)<0,即g′(x)<0,g(x)在(1,+∞)上单调递减;
∴当x=1时,g(x)取得极大值g(1)=﹣1,
∴a≥﹣1,即a的最小值为﹣1.
21.已知函数f(x)=.
(1)若f(x)在(0,e2]上单调递增,求实数a的取值范围;
(2)若f(x)≤xex+﹣1恒成立,求实数a的取值范围.
解:(1)f(x)在(0,e2]上单调递增,
即f′(x)=≥0在(0,e2]恒成立,即a≤2﹣2lnx,
显然函数y=2﹣2lnx在(0,e2]上是减函数,故ymin=y|=﹣2,
故a≤﹣2即为所求,即a的取值范围是(﹣∞,﹣2];
(2)f(x)≤xex+﹣1恒成立,显然x>0,
故原式可化为a≤x2ex﹣2lnx﹣x+1恒成立,
令g(x)=x2ex﹣2lnx﹣x+1,则g′(x)=(x+2)(xex),(x>0),
令h(x)=(x>0),>0,
故h(x)在(0,+∞)上是增函数,且h(1)=e﹣1>0,h()=,
故存在x0>0,使得h(x0)=0,即=①,
且x∈(0,x0)时,h(x)<0,即g′(x)<0,x∈(x0,+∞)时,h(x)>0,即g′(x)>0,
故x0是g(x)的极小值点,也是最小值点,
g(x)min=g(x0)=﹣2lnx0﹣x0+1②,
由①式得=,x0=﹣2lnx0,代入②式得g(x0)=2,
故a≤2即为所求,所以a的取值范围是(﹣∞,2].
22.已知函数f(x)=alnx﹣bx,其中a,b∈R.
(1)若a=1,求函数f(x)的单调区间;
(2)若b=1,函数f(x)有两个相异的零点x1,x2,求证:x1x2>e2.
解:(1)若a=1,则f(x)=lnx﹣bx的定义域是(0,+∞),f′(x)= b=,
当b≤0时,f'(x)>0,所以f(x)在(0,+∞)上单调递增;
当b>0时,令f'(x)=0,解得x=,
当0<x<时,f'(x)>0所以f(x)在(0,)上单调递增,
当x>时,f'(x)<0所以f(x)在(,+∞)上单调递减.
综上,当a≤0时,f(x)在0+∞上单调递增;
当a>0时,f(x)在(0,)上单调递增,在(,+∞)上单调递减.
(2)证明:若b=1,则函数f(x)=alnx﹣x,
因为f(x)有两个相异的零点,且f(1)=﹣1,
所以x1≠1且x2≠1,alnx1﹣x1=0,alnx2﹣x2=0,所以a=,a=,
所以方程a=有两个不相等实根,
令g(x)=,g′(x)=,
故当x∈(0,1)∪(1,e)时,g′(x)<0,当x∈(e,+∞)时,g′(x)>0,
所以g(x)在(0,1),(1,e)上单调递减,在(e,+∞)上单调递增,
因为x∈(0,1)时,g(x)<0,x∈(1,+∞)时,g(x)>0,
所以要使方程a=有两个不相等实根,则a>g(e)=e,
故不妨设x1>x2>0,alnx1=x1,alnx2=x2,
所以a(lnx1+lnx2)=aln(x1x2)=x1+x2,a(lnx1﹣lnx2)=x1﹣x2,
要证x1x2>e2 ln(x1x2)>2 >2,
因为=,
所以只需证(x1+x2)=ln>2,
只需证ln>2,即(+1)ln>2(﹣1),
令t=,则t>1,所以只要证明(t+1)lnt>2(t﹣1),t>1时恒成立,
令h(t)=(t+1)lnt 2(t﹣1),t>1,
h′(t)=lnt+﹣2=lnt+﹣1,
h″(t)=﹣=>0在(1,+∞)上恒成立,
所以h′(t)在(1,+∞)上单调递增,
因为h′(1)=0,
所以h'(t)>0恒成立,
所以h(t)在(1,+∞)单调递增,所以h(t)>h(1)=0,
所以t>1时,h(t)>0恒成立,即(t+1)lnt>2(t﹣1)恒成立,
所以x1x2>e2.
第5章 一元函数的导数及其应用 章末综合测试
选择性必修第二册高中数学人教A版【2019】
考试范围:第5章一元函数的导数及其应用;试卷满分:150分
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
第Ⅰ卷(选择题)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知f(x)是定义在R上的可导函数,若,则f′(2)=( )
A.﹣1 B. C.1 D.
2.曲线f(x)=ex+x2﹣2x﹣5在x=0处的切线的倾斜角是( )
A. B. C. D.
3.已知函数f(x)的导函数为f'(x),且,则=( )
A. B. C. D.
4.下列求导运算正确的是( )
A.(lnx)′=x B.
C.(cosx)′=sinx D.(ax)′=axlna(a>0,a≠1)
5.已知函数f(x)=x3+ax2+x+1(a∈R)有两个极值点x1,x2(x1<x2),则( )
A.或 B.x1是f(x)的极小值点
C.x1+x2= D.x1x2=﹣
6.设f(x)是定义在R上的函数,其导函数为f'(x),满足f(x)﹣xf'(x)>0,若a=4f(1),b=2f(2),c=f(4),则( )
A.a>b>c B.c>a>b C.b>c>a D.c>b>a
7.已知函数f(x)=x3﹣3x+b,且f(x)+f(﹣x)=4恒成立,若h(x)=,恰好有1个零点,则实数a的取值范围为( )
A.(﹣∞,﹣2) B.[,1]
C.(﹣∞,﹣2)∪[,1) D.[﹣2,)
8.若函数在区间(1,2)内有最小值,则实数a的取值范围为( )
A.(0,1) B. C. D.
第Ⅱ卷(非选择题)
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知定义在区间[a,b]上的函数y=f(x),f(x)是f(x)的导函数,若存在ξ∈(a,b),使得f(b)﹣f(a)=f′(ξ)(b﹣a).则称ξ为函数f(x)在[a,b]上的“中值点”.下列函数,其中在区间(﹣2,2]上至少有两个“中值点”的函数为( )
A.f(x)=sinx B.f(x)=ex
C.f(x)=ln(x+3) D.f(x)=x3﹣x+1
10.已知x2﹣y2<ex﹣e﹣y,则( )
A.ln(x+y+1)<0 B.(x+y)2+1<ex+y
C.x+y>﹣sinx﹣siny D.cosx﹣cosy>y2﹣x2
11.已知函数f(x)=ln(x+2)+ln(4﹣x),则下列说法正确的是( )
A.f(x)在区间(﹣2,1)上单调递增
B.f(x)在区间(1,+∞)上单调递减
C.f(x)在图象关于直线x=1对称
D.f(x)的图象关于点(1,0)对称
12.已知函数f(x)及其导函数f′(x)的定义域均为R,记g(x)=f′(x),f(2x﹣1)+f(3﹣2x)=f(﹣2),g(﹣1+3x)+g(﹣3x)=g,则( )
A.f(4)=0 B.g(2)=g(﹣1)
C.g()=0 D.g(2022)=g(0)
三、填空题:本题共4小题,每小题5分,共20分。
13.如图,直线l是曲线y=f(x)在点(4,f(4))处的切线,则f(4)+f′(4)的值等于 .
14.已知函数f(x)=ex﹣1﹣alnx﹣a,若曲线y=f(x)在点(1,f(1))处的切线与直线2x+y﹣1=0垂直,则切线的方程为 .
15.已知函数f(x)及其导函数f'(x)的定义域均为R,f(x)为奇函数,且f(x)﹣f'(x)>0.则不等式f(x2﹣3x+2)>0的解集为 .
16.已知不等式e2x﹣kx2+x≥lnx+lnk(k>0)恒成立,则k的最大值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.求下列函数的导数.
①;②y=(2x2﹣1)(3x+1);
③;④.
18.已知函数f(x)=exsinx﹣x+1.
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)求函数f(x)在区间上的最大值和最小值.
19.设函数,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0.
(1)求y=f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
20.已知函数f(x)=x3+ax2+x(a∈R).
(1)若函数f(x)存在两个极值点,求a的取值范围;
(2)若f(x)≥xlnx+x在(0,+∞)恒成立,求a的最小值.
21.已知函数f(x)=.
(1)若f(x)在(0,e2]上单调递增,求实数a的取值范围;
(2)若f(x)≤xex+﹣1恒成立,求实数a的取值范围.
22.已知函数f(x)=alnx﹣bx,其中a,b∈R.
(1)若a=1,求函数f(x)的单调区间;
(2)若b=1,函数f(x)有两个相异的零点x1,x2,求证:x1x2>e2.
第5章 一元函数的导数及其应用 章末综合测试
参考答案与试题解析
一.选择题(共8小题)
1.已知f(x)是定义在R上的可导函数,若,则f′(2)=( )
A.﹣1 B. C.1 D.
解:.
故选:A.
2.曲线f(x)=ex+x2﹣2x﹣5在x=0处的切线的倾斜角是( )
A. B. C. D.
解:曲线f(x)=ex+x2﹣2x﹣5,∴f′(x)=ex+2x﹣2,
故f′(0)=﹣1,
即对应切线斜率为﹣1,故曲线f(x)=ex+x2﹣2x﹣5在x=0处的切线的倾斜角是.
故选:D.
3.已知函数f(x)的导函数为f'(x),且,则=( )
A. B. C. D.
解:,
∴,
∴,
∴f(x)=x+cosx,∴.
故选:D.
4.下列求导运算正确的是( )
A.(lnx)′=x B.
C.(cosx)′=sinx D.(ax)′=axlna(a>0,a≠1)
解:∵,A项错误;
∵是个常数,∴,∴B项错误;
∵(cosx)′=﹣sinx,∴C项错误;
∵(ax)′=axlna(a>0,a≠1),∴D项正确.
故选:D.
5.已知函数f(x)=x3+ax2+x+1(a∈R)有两个极值点x1,x2(x1<x2),则( )
A.或 B.x1是f(x)的极小值点
C.x1+x2= D.x1x2=﹣
解:若函数f(x)=x3+ax2+x+1(a∈R)有两个极值点x1,x2(x1<x2),
则f′(x)=3x2+2ax+1有2个不同零点,
则Δ=4a2﹣12>0,解得a>或a<﹣,故A正确,
由于3>0,则函数f′(x)的图像开口向上,
则x1是f(x)的极大值点,故B错误,
由x1 x2=,x1+x2=﹣,则CD错误,
故选:A.
6.设f(x)是定义在R上的函数,其导函数为f'(x),满足f(x)﹣xf'(x)>0,若a=4f(1),b=2f(2),c=f(4),则( )
A.a>b>c B.c>a>b C.b>c>a D.c>b>a
解:因为f(x)满足f(x)﹣xf′(x)<0,令,
则,所以g(x)在R上是增函数,
所以g(1)<g(2)<g(4),即,
所以c>b>a.
故选:D.
7.已知函数f(x)=x3﹣3x+b,且f(x)+f(﹣x)=4恒成立,若h(x)=,恰好有1个零点,则实数a的取值范围为( )
A.(﹣∞,﹣2) B.[,1]
C.(﹣∞,﹣2)∪[,1) D.[﹣2,)
解:因为f(x)+f(﹣x)=4恒成立,所以f(x)=x3﹣3x+b的图象关于点(0,2)对称,
所以b=2,且函数f(x)=x3﹣3x+2的零点为﹣2和1,y=2﹣6x的零点为,
在同一坐标系内分别画出函数f(x)=x3﹣3x+2与y=2﹣6x的图象,
当且仅当a<﹣2或时,函数恰好有1个零点,
因此实数a的取值范围为(﹣∞,﹣2)∪.
故选:C.
8.若函数在区间(1,2)内有最小值,则实数a的取值范围为( )
A.(0,1) B. C. D.
解:由,若函数f(x)在区间(1,2)内有最小值.此时函数f(x)必定存在极值点,
由Δ=a2+4>0,设x1,x2为一元二次方程x2﹣ax﹣1=0的两根,有,
故只需要1<x2<2即可,
令g(x)=x2﹣ax﹣1,有,解得.
故选:C.
二.多选题(共4小题)
9.已知定义在区间[a,b]上的函数y=f(x),f(x)是f(x)的导函数,若存在ξ∈(a,b),使得f(b)﹣f(a)=f′(ξ)(b﹣a).则称ξ为函数f(x)在[a,b]上的“中值点”.下列函数,其中在区间(﹣2,2]上至少有两个“中值点”的函数为( )
A.f(x)=sinx B.f(x)=ex
C.f(x)=ln(x+3) D.f(x)=x3﹣x+1
解:对于A选项,f(2)﹣f(﹣2)=2sin2,f′(x)=cosx,
由f(2)﹣f(﹣2)=4f′(ξ)=4cosξ,所以,cos=,
当ξ∈[﹣2,2]时,cos2≤cosξ≤1,如下图所示:
由图可知,直线y=与曲线y=cosξ在[﹣2,2]上的图象有两个交点,A选项满足条件;
对于B选项,f(2)﹣f(﹣2)=,f′(x)=ex,
由f(2)﹣f(﹣2)=4f′(ξ)=4eξ,所以,eξ=,
因为函数y=ex在[﹣2,2]上单调递增,故方程eξ=在[﹣2,2]上不可能有两个根,B不满足条件;
对于C选项,f(2)﹣f(﹣2)=ln5,f′(x)=,
由f(2)﹣f(﹣2)=4f′(ξ)=ln5,可得=,解得ξ=﹣3∈[﹣2,2],
故函数f(x)在[﹣2,2]上只有一个“中值点”,C选项不满足条件;
对于D选项,f′(x)=3x2﹣1,f(2)﹣f(﹣2)=12,
由f(2)﹣f(﹣2)=4f′(ξ)=12,可得ξ=∈[﹣2,2],
故函数f(x)在[﹣2,2]上有两个“中值点”,D满足条件.
故选:AD.
10.已知x2﹣y2<ex﹣e﹣y,则( )
A.ln(x+y+1)<0 B.(x+y)2+1<ex+y
C.x+y>﹣sinx﹣siny D.cosx﹣cosy>y2﹣x2
解:∵x2﹣y2<ex﹣e﹣y,即e﹣y﹣(﹣y)2<ex﹣x2,
对于A:令f(x)=ex﹣x2,f'(x)=ex﹣2x,f''(x)=ex﹣2,
由f''(x)=0得x=ln2,由f'(x)>0得x>ln2,由f'(x)<0得x<ln2,
∴f'(x)在(﹣∞,ln2)上单调递减,在(ln2,+∞)上单调递增,
∴当x=ln2时,f'(x)取得极小值也是最小值,f'(x)min=f'(ln2)=2﹣2ln2>0,
∴f(x)在R上单调递增,
∵e﹣y﹣(﹣y)2<ex﹣x2,即f(﹣y)<f(x),∴﹣y<x,即x+y>0,
∴x+y+1>1,则ln(x+y+1)>ln1=0,故A错误;
对于B:要证(x+y)2+1<ex+y,即证ex+y﹣(x+y)2﹣1>0,
令t=x+y,则et﹣t2﹣1>0,令g(t)=et﹣t2﹣1,
由选项A得f(x)=ex﹣x2在R上单调递增,则g(t)=et﹣t2﹣1在[0,+∞)上单调递增,
∴g(t)>g(0)=0,故B正确;
对于C:要证x+y>﹣sinx﹣siny,即证x+sinx>﹣y+sin(﹣y),
令f(x)=x+sinx,则f'(x)=1+cosx≥0,
∴f(x)在R上单调递增,
由选项A得﹣y<x,即f(﹣y)<f(x),即x+sinx>﹣y+sin(﹣y),故C正确;
对于D:要证cosx﹣cosy>y2﹣x2,即证cosx+x2>y2+cosy,
令f(x)=cosx+x2,则f'(x)=﹣sinx+2x,f''(x)=2﹣cosx>0,
∴f'(x)在R上单调递增,
由f'(x)=0得x=0,则当x>0时,f'(x)>0,当x<0时,f'(x)<0,
∴f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增,故无法判断f(﹣y)与f(x)的大小,故D错误,
故选:BC.
11.已知函数f(x)=ln(x+2)+ln(4﹣x),则下列说法正确的是( )
A.f(x)在区间(﹣2,1)上单调递增
B.f(x)在区间(1,+∞)上单调递减
C.f(x)在图象关于直线x=1对称
D.f(x)的图象关于点(1,0)对称
解:由题意得,解得﹣2<x<4,即函数f(x)的定义域为(﹣2,4),
f(x)=ln(x+2)+ln(4﹣x)=ln(x+2)(4﹣x)=ln(﹣x2+2x+8),
令t=﹣x2+2x+8=﹣(x﹣1)2+9,则t=﹣x2+2x+8在(﹣2,1)上单调递增,在(1,4)上单调递减,
∴f(x)在(﹣2,1)上单调递增,在(1,4)上单调递减,故A正确,B错误;
f(1﹣x)=ln(3﹣x)+ln(3+x),f(1+x)=ln(3+x)+ln(3﹣x),
∴f(1﹣x)=f(1+x),则f(x)在图象关于直线x=1对称,故C正确,D错误,
故选:AC.
12.已知函数f(x)及其导函数f′(x)的定义域均为R,记g(x)=f′(x),f(2x﹣1)+f(3﹣2x)=f(﹣2),g(﹣1+3x)+g(﹣3x)=g,则( )
A.f(4)=0 B.g(2)=g(﹣1)
C.g()=0 D.g(2022)=g(0)
解:因为f(2x﹣1)+f(3﹣2x)=f(﹣2),g(x)=f′(x),g(﹣1+3x)+g(﹣3x)=g,
令x=﹣,则f(﹣2)+f(4)=f(﹣2),解得f(4)=0,故A对;
令t=2x,故f(t﹣1)+f(3﹣t)=f(﹣2),两边对t求导,则f′(t﹣1)﹣f′(3﹣t)=0,即g(t﹣1)=g(3﹣t),所以g(t)关于t=1对称,
再令t=3x,则g(﹣1+t)+g(﹣t)=g(﹣),令t=得=0,故C正确;
所以g(﹣1+t)+g(﹣t)=0,又g(t﹣1)=g(3﹣t),令t=1得g(0)+g(﹣1)=0,g(0)=g(2),故g(2)=﹣g(﹣1),故B错;
再由g(﹣1+t)+g(﹣t)=0,且g(t﹣1)=g(3﹣t),得g(3﹣t)=﹣g(﹣t),故g(t)的周期T=6,故g(2022)=g(6×337)=g(0),故D正确.
故选:ACD.
三、填空题:本题共4小题,每小题5分,共20分。
13.如图,直线l是曲线y=f(x)在点(4,f(4))处的切线,则f(4)+f′(4)的值等于 .
解:由函数的图像可得f(4)=5,直线l过点(0,3)和(4,5),
则直线l的斜率,
又由直线l是曲线y=f(x)在点(4,f(4))处的切线,则,
所以.
故答案为:.
14.已知函数f(x)=ex﹣1﹣alnx﹣a,若曲线y=f(x)在点(1,f(1))处的切线与直线2x+y﹣1=0垂直,则切线的方程为 x﹣2y=0 .
解:由题可知f′(x)=ex﹣1 ,则f'(1)=1﹣a,
因为曲线y=f(x)在(1,f(1))处的切线与直线2x+y﹣1=0垂直,
所以1 a=,解得a=.
故f(x)=ex﹣1﹣lnx﹣,f(1)=1﹣=,
即切点为(1,),切线的斜率k=,
所以切线方程为:y﹣=(x﹣1),即x﹣2y=0.
故答案为:x﹣2y=0.
15.已知函数f(x)及其导函数f'(x)的定义域均为R,f(x)为奇函数,且f(x)﹣f'(x)>0.则不等式f(x2﹣3x+2)>0的解集为 (1,2) .
解:函数f(x)及其导函数f'(x)的定义域均为R,f(0)=0,令g(x)=,则g(0)=0,
则g'(x)=,
∵f(x)﹣f'(x)>0,∴g'(x)<0,即g(x)在R上单调递减,
不等式f(x2﹣3x+2)>0,即g(x2﹣3x+2)>g(0),
∴x2﹣3x+2<0,解得1<x<2,
∴不等式f(x2﹣3x+2)>0的解集为(1,2),
故答案为:(1,2).
16.已知不等式e2x﹣kx2+x≥lnx+lnk(k>0)恒成立,则k的最大值为 e2 .
解:不等式e2x﹣kx2+x≥lnx+lnk(k>0)恒成立,
等价于e2x+lne2x≥kx2+ln(kx2)(k>0)恒成立,
令f(x)=x+lnx(x>0),
则f′(x)=1+>0,f(x)=x+lnx在(0,+∞)上单调递增,
∴e2x≥kx2(k>0)恒成立,化为≤恒成立,
令g(x)=(x>0),则g′(x)=,
当x∈(0,1)时,g′(x)<0,x∈(1,+∞)时,g′(x)>0,
∴g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴g(x)的极小值,也是最小值为g(1)=e,
∴≤e,即k≤e2,
∴k的最大值为e2,
故答案为:e2.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.求下列函数的导数.
①;②y=(2x2﹣1)(3x+1);
③;④.
解:①.
②∵y=(2x2﹣1)(3x+1)=6x3+2x2﹣3x﹣1,
∴y'=(6x3+2x2﹣3x﹣1)′=18x2+4x﹣3.
③∵,
∴.
④.
18.已知函数f(x)=exsinx﹣x+1.
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)求函数f(x)在区间上的最大值和最小值.
解:(Ⅰ)因为f(x)=exsinx﹣x+1,
所以f'(x)=ex(cosx+sinx)﹣1,
又f(0)=1,f'(0)=0,
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=1.
(Ⅱ)当,f′(x)=ex(sinx+cosx)﹣1,f″(x)=2ex cosx≥0,
所以y=f'(x)在区间上递增,
又f'(0)=0,
故当,f'(x)<f'(0)=0,
所以y=f(x)在上单减,
又当,f'(x)>f'(0)=0,
所以y=f(x)在上单增.
所以f(x)min=f(0)=1,.
19.设函数,曲线y=f(x)在点(2,f(2))处的切线方程为7x﹣4y﹣12=0.
(1)求y=f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
解析:(1)方程7x﹣4y﹣12=0可化为,当x=2时,,
又,于是,解得,故.
(2)设P(x0,y0)为曲线上任一点,由知曲线在点P(x0,y0)处的切线方程为,即
令x=0,得,从而得切线与直线x=0的交点坐标为;
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为(2x0,2x0);
所以点P(x0,y0)处的切线与直线x=0,y=x所围成的三角形面积为.
故曲线y=f(x)上任一点处的切线与直线x=0,y=x所围成的三角形面积为定值,此定值为6.
20.已知函数f(x)=x3+ax2+x(a∈R).
(1)若函数f(x)存在两个极值点,求a的取值范围;
(2)若f(x)≥xlnx+x在(0,+∞)恒成立,求a的最小值.
解:(1)∵f(x)=x3+ax2+x(a∈R)存在两个极值点,
∴f′(x)=3x2+2ax+1=0有两个不同的零点,
∴4a2﹣12>0,解得或,即a的取值范围为(﹣∞,﹣)∪(,+∞);
(2)∵x3+ax2+x≥xlnx+x在(0,+∞)上恒成立,即x3+ax2≥xlnx在(0,+∞)上恒成立 a≥(﹣x)max,x>0.
令g(x)=﹣x(x>0),
则g′(x)=﹣1=(x>0),
令t(x)=﹣x2﹣lnx+1(x>0),
则t′(x)=﹣2x﹣<0,
∴t(x)在(0,+∞)上单调递减,
又t(1)=0,
∴当x∈(0,1)时,t′(x)>0,即g′(x)>0,g(x)在(0,1)上单调递增;
当x∈(1,+∞)时,t′(x)<0,即g′(x)<0,g(x)在(1,+∞)上单调递减;
∴当x=1时,g(x)取得极大值g(1)=﹣1,
∴a≥﹣1,即a的最小值为﹣1.
21.已知函数f(x)=.
(1)若f(x)在(0,e2]上单调递增,求实数a的取值范围;
(2)若f(x)≤xex+﹣1恒成立,求实数a的取值范围.
解:(1)f(x)在(0,e2]上单调递增,
即f′(x)=≥0在(0,e2]恒成立,即a≤2﹣2lnx,
显然函数y=2﹣2lnx在(0,e2]上是减函数,故ymin=y|=﹣2,
故a≤﹣2即为所求,即a的取值范围是(﹣∞,﹣2];
(2)f(x)≤xex+﹣1恒成立,显然x>0,
故原式可化为a≤x2ex﹣2lnx﹣x+1恒成立,
令g(x)=x2ex﹣2lnx﹣x+1,则g′(x)=(x+2)(xex),(x>0),
令h(x)=(x>0),>0,
故h(x)在(0,+∞)上是增函数,且h(1)=e﹣1>0,h()=,
故存在x0>0,使得h(x0)=0,即=①,
且x∈(0,x0)时,h(x)<0,即g′(x)<0,x∈(x0,+∞)时,h(x)>0,即g′(x)>0,
故x0是g(x)的极小值点,也是最小值点,
g(x)min=g(x0)=﹣2lnx0﹣x0+1②,
由①式得=,x0=﹣2lnx0,代入②式得g(x0)=2,
故a≤2即为所求,所以a的取值范围是(﹣∞,2].
22.已知函数f(x)=alnx﹣bx,其中a,b∈R.
(1)若a=1,求函数f(x)的单调区间;
(2)若b=1,函数f(x)有两个相异的零点x1,x2,求证:x1x2>e2.
解:(1)若a=1,则f(x)=lnx﹣bx的定义域是(0,+∞),f′(x)= b=,
当b≤0时,f'(x)>0,所以f(x)在(0,+∞)上单调递增;
当b>0时,令f'(x)=0,解得x=,
当0<x<时,f'(x)>0所以f(x)在(0,)上单调递增,
当x>时,f'(x)<0所以f(x)在(,+∞)上单调递减.
综上,当a≤0时,f(x)在0+∞上单调递增;
当a>0时,f(x)在(0,)上单调递增,在(,+∞)上单调递减.
(2)证明:若b=1,则函数f(x)=alnx﹣x,
因为f(x)有两个相异的零点,且f(1)=﹣1,
所以x1≠1且x2≠1,alnx1﹣x1=0,alnx2﹣x2=0,所以a=,a=,
所以方程a=有两个不相等实根,
令g(x)=,g′(x)=,
故当x∈(0,1)∪(1,e)时,g′(x)<0,当x∈(e,+∞)时,g′(x)>0,
所以g(x)在(0,1),(1,e)上单调递减,在(e,+∞)上单调递增,
因为x∈(0,1)时,g(x)<0,x∈(1,+∞)时,g(x)>0,
所以要使方程a=有两个不相等实根,则a>g(e)=e,
故不妨设x1>x2>0,alnx1=x1,alnx2=x2,
所以a(lnx1+lnx2)=aln(x1x2)=x1+x2,a(lnx1﹣lnx2)=x1﹣x2,
要证x1x2>e2 ln(x1x2)>2 >2,
因为=,
所以只需证(x1+x2)=ln>2,
只需证ln>2,即(+1)ln>2(﹣1),
令t=,则t>1,所以只要证明(t+1)lnt>2(t﹣1),t>1时恒成立,
令h(t)=(t+1)lnt 2(t﹣1),t>1,
h′(t)=lnt+﹣2=lnt+﹣1,
h″(t)=﹣=>0在(1,+∞)上恒成立,
所以h′(t)在(1,+∞)上单调递增,
因为h′(1)=0,
所以h'(t)>0恒成立,
所以h(t)在(1,+∞)单调递增,所以h(t)>h(1)=0,
所以t>1时,h(t)>0恒成立,即(t+1)lnt>2(t﹣1)恒成立,
所以x1x2>e2.
