第一章 空间向量与立体几何 章末综合测试-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(含解析)
文档属性
| 名称 | 第一章 空间向量与立体几何 章末综合测试-2022-2023学年高二上学期数学人教A版(2019)选择性必修第一册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 651.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 05:08:44 | ||
图片预览




文档简介
绝密★启用前
第一章 空间向量与立体几何 章末综合测试
选择性必修第一册人教A版(2019)
考试范围:选择性必修第一册第一章 空间向量与立体几何;考试时间:150分钟
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知向量=3+5+,=5+﹣4,则向量=2﹣3的模为( )
A. B. C. D.
2.在棱长为1的正方体ABCD﹣A1B1C1D1中,P是棱CC1上一动点,点O是面AC的中心,则的值为( )
A.1 B. C.2 D.不确定
3.在平行六面体ABCD﹣A1B1C1D1中,点M满足.若,,,则下列向量中与相等的是( )
A. B. C. D.
4.如图,M是三棱锥P﹣ABC的底面△ABC的重心.若=x+y+z(x、y、z∈R),则x+y+z的值为( )
A. B.1 C. D.
5.设x,y∈R,向量=(x,2,2),=(1,y,1),=(1,﹣2,1),且⊥,∥,则|+|=( )
A. B. C. D.
6.在长方体ABCD﹣A1B1C1D1中,AB=3,BC=2,AA1=1,则二面角D1﹣BC﹣D的余弦值为( )
A. B. C. D.
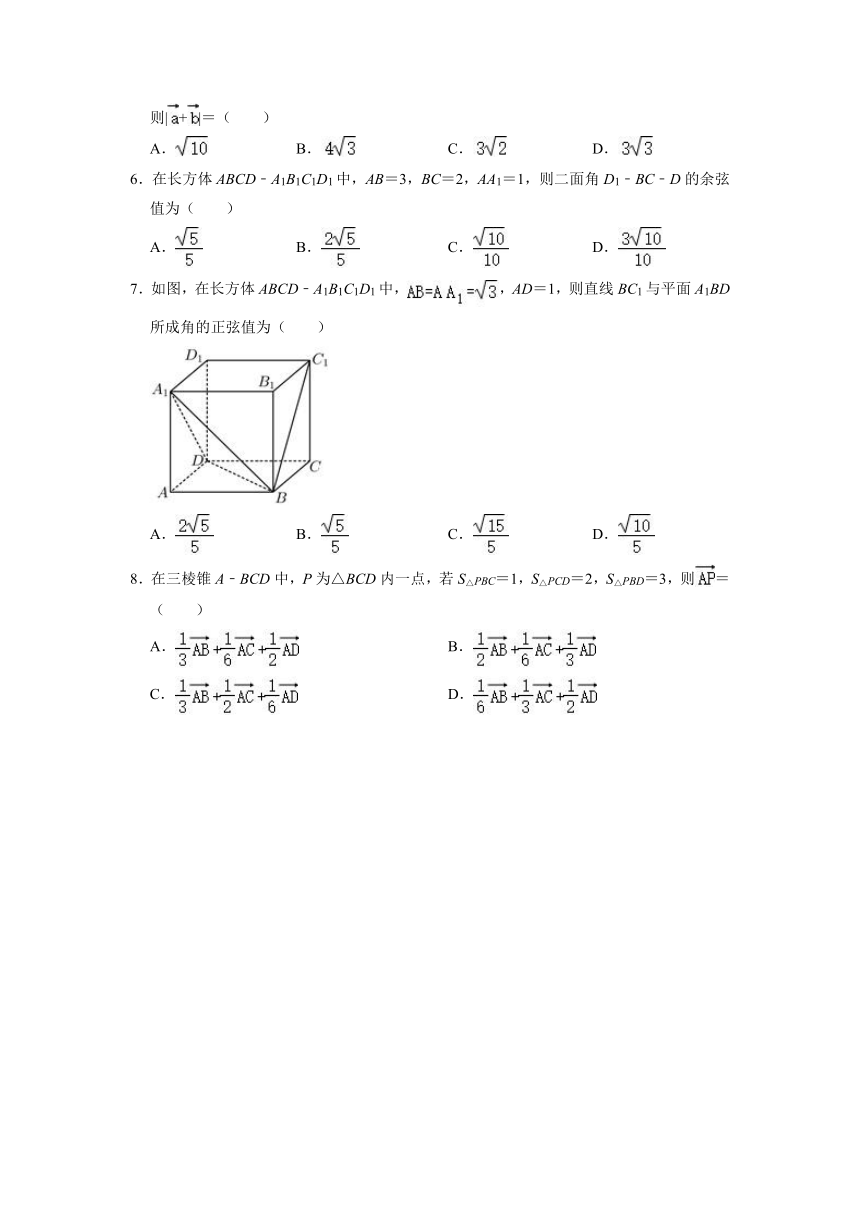
7.如图,在长方体ABCD﹣A1B1C1D1中,,AD=1,则直线BC1与平面A1BD所成角的正弦值为( )
A. B. C. D.
8.在三棱锥A﹣BCD中,P为△BCD内一点,若S△PBC=1,S△PCD=2,S△PBD=3,则=( )
A. B.
C. D.
第Ⅱ卷
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知四边形ABCD的顶点分别是A(3,﹣1,2),B(1,2,﹣1),C(﹣1,1,﹣3),D(3,﹣5,3),那么以下说话中正确的是( )
A.
B.
C.AC的中点坐标为(﹣2,0,﹣1)
D.四边形ABCD是一个梯形
10.已知空间向量,,构成的平面记为α,则下列说法正确的是( )
A.向量与α垂直
B.向量与α平行
C.若与分别是l1与l2的方向向量,则直线l1,l2所成的角的余弦值为
D.向量在向量上的投影向量为(0,﹣2,0)
11.关于空间向量,以下说法正确的是( )
A.两个非零向量,,若,则
B.若对空间中任意一点O,有,则P,A,B,C四点共面
C.设是空间中的一组基底,则也是空间的一组基底
D.若空间四个点P,A,B,C,,则A,B,C三点共线
12.已知正四棱台ABCD﹣A1B1C1D1,下底面ABCD边长为4,上底面边长为2,侧棱长为2,则( )
A.它的表面积是
B.它的外接球球心在该四棱台的内部
C.侧棱与下底面所成的角为
D.它的体积比半径为的球的体积小
三.填空题(共4小题)
13.已知空间中三点A(0,2,3),B(﹣2,1,6),C(1,﹣1,5),则以向量、为一组邻边的平行四边形的面积为 .
14.棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是CC1,D1A1的中点,则cos = .
15.已知向量,,,则的坐标为 .
16.已知空间向量,,都是单位向量,且⊥,⊥,与的夹角为60°,若P为空间任意一点,且||=1,满足| |≤| |≤| |,则 的最大值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知空间三点A(﹣2,0,2),B(﹣1,1,2),C(﹣3,0,4),设,.
(1)若,,求;
(2)求,夹角的余弦值.
18.如图,在直三棱柱ABC﹣A1B1C1,E,F,G分别为A1B1,CC1,BB1的中点,分别记,,为,,.
(1)用,,表示;
(2)若AB=AC=AA1=2,AB⊥AC,求|+2|.
19.如图,四棱锥P﹣ABCD的底面ABCD是边长为2的正方形,平面PAD⊥平面ABCD,△PAD是斜边PA的长为的等腰直角三角形,E,F分别是棱PA,PC的中点,M是棱BC上一点.
(1)求证:平面DFM⊥平面PBC;
(2)若直线MF与平面ABCD所成角的正切值为,求锐二面角E﹣DM﹣F的余弦值.
20. 如图,在多面体ABCDE中,平面ABC⊥平面ACDE,四边形ACDE是等腰梯形,ED∥AC,AB⊥AC,.
(1)若AB=1,求BD与平面ACDE所成角的正弦值;
(2)若平面BDE与平面BCD的夹角为,求AB的长.
21.已知直角三角形ABC中∠BAC=90°,CA=2AB=4,D,E分别是AC,BC边中点,将△CDE和△BAE分别沿着DE,AE翻折,形成三棱锥P﹣ADE,M是AD中点.
(1)证明:PM⊥平面ADE;
(2)若直线PM上存在一点Q,使得QE与平面PAE所成角的正弦值为,求QM的值.
22.如图,在四棱锥P﹣ABCD中,已知底面ABCD是正方形,PC⊥底面ABCD,且PC=BC=1,E是棱PB上一点.
(1)若PD∥平面ACE,证明:E是PB的中点;
(2)线段PB上是否存在点E,使二面角P﹣AC﹣E的余弦值是?若存在,求的值;若不存在,请说明理由.
第一章 空间向量与立体几何 章末综合测试
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知向量=3+5+,=5+﹣4,则向量=2﹣3的模为( )
A. B. C. D.
解:因为向量=3+5+,=5+﹣4,
则=(3,5,1),=(5,1,﹣4),
所以向量=2﹣3=2(3,5,1)﹣3(5,1,﹣4)=(﹣9,7,14),
所以||==.
故选:B.
2.在棱长为1的正方体ABCD﹣A1B1C1D1中,P是棱CC1上一动点,点O是面AC的中心,则的值为( )
A.1 B. C.2 D.不确定
解:建立如图所示空间直角坐标系,
则A(1,0,0),P(0,1,x)(0≤x≤1),O(,,0),
∴=(﹣1,1,x)(0≤x≤1),=(﹣,,0),
∴= 1×( )+1×=1.
故选:A.
3.在平行六面体ABCD﹣A1B1C1D1中,点M满足.若,,,则下列向量中与相等的是( )
A. B. C. D.
解:平行六面体ABCD﹣A1B1C1D1中,点M满足.若,,,
所以.
故选:C.
4.如图,M是三棱锥P﹣ABC的底面△ABC的重心.若=x+y+z(x、y、z∈R),则x+y+z的值为( )
A. B.1 C. D.
解:由于M是三棱锥P﹣ABC的底面△ABC的重心,
所以,
利用向量的线性运算,
即.
故选:C.
5.设x,y∈R,向量=(x,2,2),=(1,y,1),=(1,﹣2,1),且⊥,∥,则|+|=( )
A. B. C. D.
解:向量,且,
∴,解得,
∴,
∴.
故选:C.
6.在长方体ABCD﹣A1B1C1D1中,AB=3,BC=2,AA1=1,则二面角D1﹣BC﹣D的余弦值为( )
A. B. C. D.
解:如图所示,
在长方体ABCD﹣A1B1C1D1中,BC⊥平面CC1D1D,
CD1 平面CC1D1D,所以BC⊥CD1,又CD⊥BC,
所以∠DCD1为二面角D1﹣BC﹣D的平面角,
因为DD1=AA1=1,CD=AB=3,所以CD1=,
所以cos∠DCD1===,
即二面角D1﹣BC﹣D的余弦值为.
故选:D.
7.如图,在长方体ABCD﹣A1B1C1D1中,,AD=1,则直线BC1与平面A1BD所成角的正弦值为( )
A. B. C. D.
解:以D为原点,分别以DA,DC,DD1为x,y,z轴,建立空间直角坐标系如图,
则A1(1,0,),B(1,,0),C1(0,,),
=(1,0,),=(1,,0),=(﹣1,0,)
设平面A1BD的法向量为=(x,y,z),
则,
令x=,y=﹣1,z=﹣1,∴=(,﹣1,﹣1),
直线BC1与平面A1BD所成的角为α,
sinα=|cos<,>|=||=||=.
故选:C.
8.在三棱锥A﹣BCD中,P为△BCD内一点,若S△PBC=1,S△PCD=2,S△PBD=3,则=( )
A. B.
C. D.
解:三棱锥A﹣BCD中,P为△BCD内一点,如图所示:
延长PB至B1,使得PB1=2PB,延长PC至C1,使得PC1=3PC,连接DB1,B1C1,C1D,
因为S△PBC=1,S△PCD=2,S△PBD=3,所以==,
所以P为△B1C1D的重心,所以++=,
即+2+3=,
所以(﹣)+2(﹣)+3(﹣)=,
所以=++.
故选:C.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知四边形ABCD的顶点分别是A(3,﹣1,2),B(1,2,﹣1),C(﹣1,1,﹣3),D(3,﹣5,3),那么以下说话中正确的是( )
A.
B.
C.AC的中点坐标为(﹣2,0,﹣1)
D.四边形ABCD是一个梯形
解:∵A(3,﹣1,2),B(1,2,﹣1),C(﹣1,1,﹣3),D(3,﹣5,3),
∴,,故A正确,B错误,AC的中点坐标为(1,0,),故C错误,
,和共线,即AB∥CD,
,,与不共线,即AD与BC不平行,
故四边形ABCD为梯形.
故选:AD.
10.已知空间向量,,构成的平面记为α,则下列说法正确的是( )
A.向量与α垂直
B.向量与α平行
C.若与分别是l1与l2的方向向量,则直线l1,l2所成的角的余弦值为
D.向量在向量上的投影向量为(0,﹣2,0)
解:对于A,∵,,
∴,,
又与不平行,
∴,A正确;
对于B,∵,
∴共面,则与α平行,B正确;
对于C,∵,
∴l1,l2所成角的余弦值为,C错误;
对于D,∵,,
∴在上的投影向量为,D错误.
故选:AB.
11.关于空间向量,以下说法正确的是( )
A.两个非零向量,,若,则
B.若对空间中任意一点O,有,则P,A,B,C四点共面
C.设是空间中的一组基底,则也是空间的一组基底
D.若空间四个点P,A,B,C,,则A,B,C三点共线
解:对于A,非零向量,,若,则,故A正确;
对于B,若对空间中任意一点O,有,
因为,所以P,A,B,C四点共面,故B正确;
对于C,设是空间中的一组基底,由向量的加法法则可知:,
所以不能构成空间的一组基底,故C错误;
对于D,若空间四个点P,A,B,C,,
由共线向量定理可知:A,B,C三点共线,故D正确,
故选:ABD.
12.已知正四棱台ABCD﹣A1B1C1D1,下底面ABCD边长为4,上底面边长为2,侧棱长为2,则( )
A.它的表面积是
B.它的外接球球心在该四棱台的内部
C.侧棱与下底面所成的角为
D.它的体积比半径为的球的体积小
解:如图,
正四棱台ABCD﹣A1B1C1D1,O1,O2分别是上下底面的中心,点E1,E分别是棱B1C1,BC的中点,
在直角梯形O1O2BB1中,,则正四棱台高,
在直角梯形O1O2EE1中,O1E1=1,O2E=2,则正四棱台斜高,
对于A,正四棱台ABCD﹣A1B1C1D1表面积,A正确;
对于B,正四棱台ABCD﹣A1B1C1D1的外接球球心O在直线O1O2上,
设球半径为R,
点O到平面A1B1C1D1的距离,
点O到平面ABCD的距离,
由d2≥0,得R2≥8,
因此,即点O在线段O1O2的延长线上,B不正确;
对于C,侧棱与下底面所成的角为,C不正确;
对于D,正四棱台ABCD﹣A1B1C1D1体积,
半径为的球的体积为,D正确.
故选:AD.
三.填空题(共4小题)
13.已知空间中三点A(0,2,3),B(﹣2,1,6),C(1,﹣1,5),则以向量、为一组邻边的平行四边形的面积为 7 .
解:∵A(0,2,3),B(﹣2,1,6),C(1,﹣1,5),
∴=(﹣2,﹣1,3),=(1,﹣3,2),||=,||=,
∴cos∠BAC==,
∴∠BAC=60°,
∴S=×sin60°=7.
故答案为:7.
14.棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是CC1,D1A1的中点,则cos = ﹣ .
解:如图建立空间直角坐标系,
则A(1,0,0),B(1,1,0),
点E,F分别是CC1,D1A1的中点,
,,
所以,,
所以,,,
所以.
故答案为:.
15.已知向量,,,则的坐标为 (10,﹣3,17) .
解:向量,,,
则.
故答案为:(10,﹣3,17).
16.已知空间向量,,都是单位向量,且⊥,⊥,与的夹角为60°,若P为空间任意一点,且||=1,满足| |≤| |≤| |,则 的最大值为 .
解:由题知,,,
再设,且x,y,z>0,x2+y2+z2=1,
代入已知的不等式得,可得,z≥y,
所以,解得,
故=y.
故答案为:.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知空间三点A(﹣2,0,2),B(﹣1,1,2),C(﹣3,0,4),设,.
(1)若,,求;
(2)求,夹角的余弦值.
解:(1)B(﹣1,1,2),C(﹣3,0,4),
则,
∵,
∴可设,λ≠0,
∵,
∴,解得λ=±2,
∴或;
(2)∵A(﹣2,0,2),B(﹣1,1,2),C(﹣3,0,4),
∴,,
∴===.
18.如图,在直三棱柱ABC﹣A1B1C1,E,F,G分别为A1B1,CC1,BB1的中点,分别记,,为,,.
(1)用,,表示;
(2)若AB=AC=AA1=2,AB⊥AC,求|+2|.
解:(1)=﹣=+﹣=﹣﹣=﹣﹣,
=+=﹣=﹣.
(2)因为直三棱柱ABC﹣A1B1C1,且AB⊥AC,
所以 = = =0,
所以|+2|2=|﹣﹣+2×(﹣)|2=|﹣+|2=2+2+2+ ﹣3 ﹣ =2+2+2=×4+4+×4=14,
所以|+2|=.
19.如图,四棱锥P﹣ABCD的底面ABCD是边长为2的正方形,平面PAD⊥平面ABCD,△PAD是斜边PA的长为的等腰直角三角形,E,F分别是棱PA,PC的中点,M是棱BC上一点.
(1)求证:平面DFM⊥平面PBC;
(2)若直线MF与平面ABCD所成角的正切值为,求锐二面角E﹣DM﹣F的余弦值.
证明:(1)依题意可得:PD⊥DA,DP=DA=DC=2,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,且PD⊥AD,
∴PD⊥平面ABCD,
∵BC 平面ABCD,
∴PD⊥BC,
又∵BC⊥DC,PD∩DC=D,DC、PD 平面PDC,
∴BC⊥平面PDC,又DF 平面PDC,
∴BC⊥DF,
又在Rt△PDC中,F是PC中点,则有DF⊥PC,
∵DF⊥BC,DF⊥PC,PC∩BC=C,且BC、PC 平面PBC,
∴DF⊥平面PBC,
又∵DF 平面DFM,
∴平面DFM⊥平面PBC;
解:(2)取CD的中点N,连接FN、MN,以DA,DC,DP所在直线为x,y,z轴,建立如图所示空间直角坐标系,
∵FN⊥平面ABCD,∴直线MF与平面ABCD所成角为∠FMN,
∵直线MF与平面ABCD所成角的正切值为,
∴,则MN=,
∴CM==,
可得M是BC靠近C的三等分点,则,
∴=(﹣1,0,﹣1),=(,2,0),
设平面EDM的法向量为=(x,y,z),
则 ,
令x=﹣3,则平面EDM的法向量为=(﹣3,1,3),
同理平面DMF的法向量,
∴,
所以锐二面角E﹣DM﹣F的余弦值是.
20. 如图,在多面体ABCDE中,平面ABC⊥平面ACDE,四边形ACDE是等腰梯形,ED∥AC,AB⊥AC,.
(1)若AB=1,求BD与平面ACDE所成角的正弦值;
(2)若平面BDE与平面BCD的夹角为,求AB的长.
解:(1)因为平面ABC⊥平面ACDE,AB⊥AC,平面ABC∩平面ACDE=AC,AB 平面ABC,
所以AB⊥平面ACDE,
连接AD,可得BD与平面ACDE所成角为∠BDA.
由等腰梯形ACDE,DE=1,AC=2,CD=1,可得CH=,高DH=,
AD==,
又AB=1,所以tan∠BDA==,则∠BDA=,
即BD与平面ACDE所成角的正弦值为;
(2)由面面垂直的性质定理可得DH⊥平面ABC,
以A为坐标原点,以AC,AB所在的直线为x,y轴,以过A平行于DH的直线为z轴,建立空间直角坐标系.
设AB=c,则B(0,c,0),C(2,0,0),E(,0,),D(,0,),
可得=(2,﹣c,0),=(,﹣c,),=(﹣1,0,0),
设平面BCD的法向量为=(x1,y1,z1),由 =0,且 =0,即2x1﹣cy1=0,x1﹣cy1+z1=0,
取x1=c,则y1=2,z1=c,即=(c,2,c),
设平面BDE的法向量为=(x2,y2,z2,由 =0, =0,可得﹣x2=0,x2﹣cy2+z2=0,
可令z2=c,则y2=,即有=(0,,c),
则cos<,>==,解得c=,
即AB=.
21.已知直角三角形ABC中∠BAC=90°,CA=2AB=4,D,E分别是AC,BC边中点,将△CDE和△BAE分别沿着DE,AE翻折,形成三棱锥P﹣ADE,M是AD中点.
(1)证明:PM⊥平面ADE;
(2)若直线PM上存在一点Q,使得QE与平面PAE所成角的正弦值为,求QM的值.
(1)证明:由题意知,PA=BA=2,PD=CD=CA=2,
所以PA=PD=2,
又M为AD中点,所以PM⊥AD,
因为D,E分别是AC,BC边中点,所以DE∥AB,
因为∠BAC=90°,所以DE⊥AD,DE⊥CD,即DE⊥PD,
因为AD∩PD=D,AD、PD 平面PAD,所以DE⊥平面PAD,
又PM 平面PAD,所以PM⊥DE,
因为AD∩DE=D,AD、DE 平面ADE,
所以PM⊥平面ADE.
(2)解:以M为坐标原点,MD,MP分别为x,z轴,作My∥DE,建立如图所示的空间直角坐标系,
由PD=2,PA=2,DE=AB=1,
得A(﹣1,0,0),D(1,0,0),P(0,0,),E(1,1,0),
所以=(﹣1,0,﹣),=(2,1,0),
设平面PAE的法向量为=(x,y,z),则,即,
令z=﹣1,则x=,y=﹣2,所以=(,﹣2,﹣1),
设Q(0,0,t),则,
因为QE与平面PAE所成角的正弦值为,所以,解得,
所以Q(0,0,),
故.
22.如图,在四棱锥P﹣ABCD中,已知底面ABCD是正方形,PC⊥底面ABCD,且PC=BC=1,E是棱PB上一点.
(1)若PD∥平面ACE,证明:E是PB的中点;
(2)线段PB上是否存在点E,使二面角P﹣AC﹣E的余弦值是?若存在,求的值;若不存在,请说明理由.
解:(1)证明:如图,连接BD交AC于点O,连接EO,
∵ABCD是正方形,∴O是BD的中点,
又PD∥平面ACE,PD 平面PBD,平面PBD∩平面ACE=EO,
∴PD∥EO,
∵O为BD的中点,∴E是PB的中点;
(2)以C为坐标原点,建立如图所示的空间直角坐标系,
则C(0,0,0),A(1,1,0),B(1,0,0),D(0,1,0),P(0,0,1),
设(0<λ<1),设E(a,b,c),
∴,,,则a=λ,b=0,c=1﹣λ,
则E(λ,0,1﹣λ),,,
由BD⊥AC且BD⊥PC,可知是平面PAC的一个法向量.
设为平面EAC的法向量,
则,即,取,
∴,
解得,即.
第一章 空间向量与立体几何 章末综合测试
选择性必修第一册人教A版(2019)
考试范围:选择性必修第一册第一章 空间向量与立体几何;考试时间:150分钟
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知向量=3+5+,=5+﹣4,则向量=2﹣3的模为( )
A. B. C. D.
2.在棱长为1的正方体ABCD﹣A1B1C1D1中,P是棱CC1上一动点,点O是面AC的中心,则的值为( )
A.1 B. C.2 D.不确定
3.在平行六面体ABCD﹣A1B1C1D1中,点M满足.若,,,则下列向量中与相等的是( )
A. B. C. D.
4.如图,M是三棱锥P﹣ABC的底面△ABC的重心.若=x+y+z(x、y、z∈R),则x+y+z的值为( )
A. B.1 C. D.
5.设x,y∈R,向量=(x,2,2),=(1,y,1),=(1,﹣2,1),且⊥,∥,则|+|=( )
A. B. C. D.
6.在长方体ABCD﹣A1B1C1D1中,AB=3,BC=2,AA1=1,则二面角D1﹣BC﹣D的余弦值为( )
A. B. C. D.
7.如图,在长方体ABCD﹣A1B1C1D1中,,AD=1,则直线BC1与平面A1BD所成角的正弦值为( )
A. B. C. D.
8.在三棱锥A﹣BCD中,P为△BCD内一点,若S△PBC=1,S△PCD=2,S△PBD=3,则=( )
A. B.
C. D.
第Ⅱ卷
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知四边形ABCD的顶点分别是A(3,﹣1,2),B(1,2,﹣1),C(﹣1,1,﹣3),D(3,﹣5,3),那么以下说话中正确的是( )
A.
B.
C.AC的中点坐标为(﹣2,0,﹣1)
D.四边形ABCD是一个梯形
10.已知空间向量,,构成的平面记为α,则下列说法正确的是( )
A.向量与α垂直
B.向量与α平行
C.若与分别是l1与l2的方向向量,则直线l1,l2所成的角的余弦值为
D.向量在向量上的投影向量为(0,﹣2,0)
11.关于空间向量,以下说法正确的是( )
A.两个非零向量,,若,则
B.若对空间中任意一点O,有,则P,A,B,C四点共面
C.设是空间中的一组基底,则也是空间的一组基底
D.若空间四个点P,A,B,C,,则A,B,C三点共线
12.已知正四棱台ABCD﹣A1B1C1D1,下底面ABCD边长为4,上底面边长为2,侧棱长为2,则( )
A.它的表面积是
B.它的外接球球心在该四棱台的内部
C.侧棱与下底面所成的角为
D.它的体积比半径为的球的体积小
三.填空题(共4小题)
13.已知空间中三点A(0,2,3),B(﹣2,1,6),C(1,﹣1,5),则以向量、为一组邻边的平行四边形的面积为 .
14.棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是CC1,D1A1的中点,则cos = .
15.已知向量,,,则的坐标为 .
16.已知空间向量,,都是单位向量,且⊥,⊥,与的夹角为60°,若P为空间任意一点,且||=1,满足| |≤| |≤| |,则 的最大值为 .
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知空间三点A(﹣2,0,2),B(﹣1,1,2),C(﹣3,0,4),设,.
(1)若,,求;
(2)求,夹角的余弦值.
18.如图,在直三棱柱ABC﹣A1B1C1,E,F,G分别为A1B1,CC1,BB1的中点,分别记,,为,,.
(1)用,,表示;
(2)若AB=AC=AA1=2,AB⊥AC,求|+2|.
19.如图,四棱锥P﹣ABCD的底面ABCD是边长为2的正方形,平面PAD⊥平面ABCD,△PAD是斜边PA的长为的等腰直角三角形,E,F分别是棱PA,PC的中点,M是棱BC上一点.
(1)求证:平面DFM⊥平面PBC;
(2)若直线MF与平面ABCD所成角的正切值为,求锐二面角E﹣DM﹣F的余弦值.
20. 如图,在多面体ABCDE中,平面ABC⊥平面ACDE,四边形ACDE是等腰梯形,ED∥AC,AB⊥AC,.
(1)若AB=1,求BD与平面ACDE所成角的正弦值;
(2)若平面BDE与平面BCD的夹角为,求AB的长.
21.已知直角三角形ABC中∠BAC=90°,CA=2AB=4,D,E分别是AC,BC边中点,将△CDE和△BAE分别沿着DE,AE翻折,形成三棱锥P﹣ADE,M是AD中点.
(1)证明:PM⊥平面ADE;
(2)若直线PM上存在一点Q,使得QE与平面PAE所成角的正弦值为,求QM的值.
22.如图,在四棱锥P﹣ABCD中,已知底面ABCD是正方形,PC⊥底面ABCD,且PC=BC=1,E是棱PB上一点.
(1)若PD∥平面ACE,证明:E是PB的中点;
(2)线段PB上是否存在点E,使二面角P﹣AC﹣E的余弦值是?若存在,求的值;若不存在,请说明理由.
第一章 空间向量与立体几何 章末综合测试
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知向量=3+5+,=5+﹣4,则向量=2﹣3的模为( )
A. B. C. D.
解:因为向量=3+5+,=5+﹣4,
则=(3,5,1),=(5,1,﹣4),
所以向量=2﹣3=2(3,5,1)﹣3(5,1,﹣4)=(﹣9,7,14),
所以||==.
故选:B.
2.在棱长为1的正方体ABCD﹣A1B1C1D1中,P是棱CC1上一动点,点O是面AC的中心,则的值为( )
A.1 B. C.2 D.不确定
解:建立如图所示空间直角坐标系,
则A(1,0,0),P(0,1,x)(0≤x≤1),O(,,0),
∴=(﹣1,1,x)(0≤x≤1),=(﹣,,0),
∴= 1×( )+1×=1.
故选:A.
3.在平行六面体ABCD﹣A1B1C1D1中,点M满足.若,,,则下列向量中与相等的是( )
A. B. C. D.
解:平行六面体ABCD﹣A1B1C1D1中,点M满足.若,,,
所以.
故选:C.
4.如图,M是三棱锥P﹣ABC的底面△ABC的重心.若=x+y+z(x、y、z∈R),则x+y+z的值为( )
A. B.1 C. D.
解:由于M是三棱锥P﹣ABC的底面△ABC的重心,
所以,
利用向量的线性运算,
即.
故选:C.
5.设x,y∈R,向量=(x,2,2),=(1,y,1),=(1,﹣2,1),且⊥,∥,则|+|=( )
A. B. C. D.
解:向量,且,
∴,解得,
∴,
∴.
故选:C.
6.在长方体ABCD﹣A1B1C1D1中,AB=3,BC=2,AA1=1,则二面角D1﹣BC﹣D的余弦值为( )
A. B. C. D.
解:如图所示,
在长方体ABCD﹣A1B1C1D1中,BC⊥平面CC1D1D,
CD1 平面CC1D1D,所以BC⊥CD1,又CD⊥BC,
所以∠DCD1为二面角D1﹣BC﹣D的平面角,
因为DD1=AA1=1,CD=AB=3,所以CD1=,
所以cos∠DCD1===,
即二面角D1﹣BC﹣D的余弦值为.
故选:D.
7.如图,在长方体ABCD﹣A1B1C1D1中,,AD=1,则直线BC1与平面A1BD所成角的正弦值为( )
A. B. C. D.
解:以D为原点,分别以DA,DC,DD1为x,y,z轴,建立空间直角坐标系如图,
则A1(1,0,),B(1,,0),C1(0,,),
=(1,0,),=(1,,0),=(﹣1,0,)
设平面A1BD的法向量为=(x,y,z),
则,
令x=,y=﹣1,z=﹣1,∴=(,﹣1,﹣1),
直线BC1与平面A1BD所成的角为α,
sinα=|cos<,>|=||=||=.
故选:C.
8.在三棱锥A﹣BCD中,P为△BCD内一点,若S△PBC=1,S△PCD=2,S△PBD=3,则=( )
A. B.
C. D.
解:三棱锥A﹣BCD中,P为△BCD内一点,如图所示:
延长PB至B1,使得PB1=2PB,延长PC至C1,使得PC1=3PC,连接DB1,B1C1,C1D,
因为S△PBC=1,S△PCD=2,S△PBD=3,所以==,
所以P为△B1C1D的重心,所以++=,
即+2+3=,
所以(﹣)+2(﹣)+3(﹣)=,
所以=++.
故选:C.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5分,部分选对的得2分,有选错的得0分。
9.已知四边形ABCD的顶点分别是A(3,﹣1,2),B(1,2,﹣1),C(﹣1,1,﹣3),D(3,﹣5,3),那么以下说话中正确的是( )
A.
B.
C.AC的中点坐标为(﹣2,0,﹣1)
D.四边形ABCD是一个梯形
解:∵A(3,﹣1,2),B(1,2,﹣1),C(﹣1,1,﹣3),D(3,﹣5,3),
∴,,故A正确,B错误,AC的中点坐标为(1,0,),故C错误,
,和共线,即AB∥CD,
,,与不共线,即AD与BC不平行,
故四边形ABCD为梯形.
故选:AD.
10.已知空间向量,,构成的平面记为α,则下列说法正确的是( )
A.向量与α垂直
B.向量与α平行
C.若与分别是l1与l2的方向向量,则直线l1,l2所成的角的余弦值为
D.向量在向量上的投影向量为(0,﹣2,0)
解:对于A,∵,,
∴,,
又与不平行,
∴,A正确;
对于B,∵,
∴共面,则与α平行,B正确;
对于C,∵,
∴l1,l2所成角的余弦值为,C错误;
对于D,∵,,
∴在上的投影向量为,D错误.
故选:AB.
11.关于空间向量,以下说法正确的是( )
A.两个非零向量,,若,则
B.若对空间中任意一点O,有,则P,A,B,C四点共面
C.设是空间中的一组基底,则也是空间的一组基底
D.若空间四个点P,A,B,C,,则A,B,C三点共线
解:对于A,非零向量,,若,则,故A正确;
对于B,若对空间中任意一点O,有,
因为,所以P,A,B,C四点共面,故B正确;
对于C,设是空间中的一组基底,由向量的加法法则可知:,
所以不能构成空间的一组基底,故C错误;
对于D,若空间四个点P,A,B,C,,
由共线向量定理可知:A,B,C三点共线,故D正确,
故选:ABD.
12.已知正四棱台ABCD﹣A1B1C1D1,下底面ABCD边长为4,上底面边长为2,侧棱长为2,则( )
A.它的表面积是
B.它的外接球球心在该四棱台的内部
C.侧棱与下底面所成的角为
D.它的体积比半径为的球的体积小
解:如图,
正四棱台ABCD﹣A1B1C1D1,O1,O2分别是上下底面的中心,点E1,E分别是棱B1C1,BC的中点,
在直角梯形O1O2BB1中,,则正四棱台高,
在直角梯形O1O2EE1中,O1E1=1,O2E=2,则正四棱台斜高,
对于A,正四棱台ABCD﹣A1B1C1D1表面积,A正确;
对于B,正四棱台ABCD﹣A1B1C1D1的外接球球心O在直线O1O2上,
设球半径为R,
点O到平面A1B1C1D1的距离,
点O到平面ABCD的距离,
由d2≥0,得R2≥8,
因此,即点O在线段O1O2的延长线上,B不正确;
对于C,侧棱与下底面所成的角为,C不正确;
对于D,正四棱台ABCD﹣A1B1C1D1体积,
半径为的球的体积为,D正确.
故选:AD.
三.填空题(共4小题)
13.已知空间中三点A(0,2,3),B(﹣2,1,6),C(1,﹣1,5),则以向量、为一组邻边的平行四边形的面积为 7 .
解:∵A(0,2,3),B(﹣2,1,6),C(1,﹣1,5),
∴=(﹣2,﹣1,3),=(1,﹣3,2),||=,||=,
∴cos∠BAC==,
∴∠BAC=60°,
∴S=×sin60°=7.
故答案为:7.
14.棱长为1的正方体ABCD﹣A1B1C1D1中,点E,F分别是CC1,D1A1的中点,则cos = ﹣ .
解:如图建立空间直角坐标系,
则A(1,0,0),B(1,1,0),
点E,F分别是CC1,D1A1的中点,
,,
所以,,
所以,,,
所以.
故答案为:.
15.已知向量,,,则的坐标为 (10,﹣3,17) .
解:向量,,,
则.
故答案为:(10,﹣3,17).
16.已知空间向量,,都是单位向量,且⊥,⊥,与的夹角为60°,若P为空间任意一点,且||=1,满足| |≤| |≤| |,则 的最大值为 .
解:由题知,,,
再设,且x,y,z>0,x2+y2+z2=1,
代入已知的不等式得,可得,z≥y,
所以,解得,
故=y.
故答案为:.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.已知空间三点A(﹣2,0,2),B(﹣1,1,2),C(﹣3,0,4),设,.
(1)若,,求;
(2)求,夹角的余弦值.
解:(1)B(﹣1,1,2),C(﹣3,0,4),
则,
∵,
∴可设,λ≠0,
∵,
∴,解得λ=±2,
∴或;
(2)∵A(﹣2,0,2),B(﹣1,1,2),C(﹣3,0,4),
∴,,
∴===.
18.如图,在直三棱柱ABC﹣A1B1C1,E,F,G分别为A1B1,CC1,BB1的中点,分别记,,为,,.
(1)用,,表示;
(2)若AB=AC=AA1=2,AB⊥AC,求|+2|.
解:(1)=﹣=+﹣=﹣﹣=﹣﹣,
=+=﹣=﹣.
(2)因为直三棱柱ABC﹣A1B1C1,且AB⊥AC,
所以 = = =0,
所以|+2|2=|﹣﹣+2×(﹣)|2=|﹣+|2=2+2+2+ ﹣3 ﹣ =2+2+2=×4+4+×4=14,
所以|+2|=.
19.如图,四棱锥P﹣ABCD的底面ABCD是边长为2的正方形,平面PAD⊥平面ABCD,△PAD是斜边PA的长为的等腰直角三角形,E,F分别是棱PA,PC的中点,M是棱BC上一点.
(1)求证:平面DFM⊥平面PBC;
(2)若直线MF与平面ABCD所成角的正切值为,求锐二面角E﹣DM﹣F的余弦值.
证明:(1)依题意可得:PD⊥DA,DP=DA=DC=2,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,且PD⊥AD,
∴PD⊥平面ABCD,
∵BC 平面ABCD,
∴PD⊥BC,
又∵BC⊥DC,PD∩DC=D,DC、PD 平面PDC,
∴BC⊥平面PDC,又DF 平面PDC,
∴BC⊥DF,
又在Rt△PDC中,F是PC中点,则有DF⊥PC,
∵DF⊥BC,DF⊥PC,PC∩BC=C,且BC、PC 平面PBC,
∴DF⊥平面PBC,
又∵DF 平面DFM,
∴平面DFM⊥平面PBC;
解:(2)取CD的中点N,连接FN、MN,以DA,DC,DP所在直线为x,y,z轴,建立如图所示空间直角坐标系,
∵FN⊥平面ABCD,∴直线MF与平面ABCD所成角为∠FMN,
∵直线MF与平面ABCD所成角的正切值为,
∴,则MN=,
∴CM==,
可得M是BC靠近C的三等分点,则,
∴=(﹣1,0,﹣1),=(,2,0),
设平面EDM的法向量为=(x,y,z),
则 ,
令x=﹣3,则平面EDM的法向量为=(﹣3,1,3),
同理平面DMF的法向量,
∴,
所以锐二面角E﹣DM﹣F的余弦值是.
20. 如图,在多面体ABCDE中,平面ABC⊥平面ACDE,四边形ACDE是等腰梯形,ED∥AC,AB⊥AC,.
(1)若AB=1,求BD与平面ACDE所成角的正弦值;
(2)若平面BDE与平面BCD的夹角为,求AB的长.
解:(1)因为平面ABC⊥平面ACDE,AB⊥AC,平面ABC∩平面ACDE=AC,AB 平面ABC,
所以AB⊥平面ACDE,
连接AD,可得BD与平面ACDE所成角为∠BDA.
由等腰梯形ACDE,DE=1,AC=2,CD=1,可得CH=,高DH=,
AD==,
又AB=1,所以tan∠BDA==,则∠BDA=,
即BD与平面ACDE所成角的正弦值为;
(2)由面面垂直的性质定理可得DH⊥平面ABC,
以A为坐标原点,以AC,AB所在的直线为x,y轴,以过A平行于DH的直线为z轴,建立空间直角坐标系.
设AB=c,则B(0,c,0),C(2,0,0),E(,0,),D(,0,),
可得=(2,﹣c,0),=(,﹣c,),=(﹣1,0,0),
设平面BCD的法向量为=(x1,y1,z1),由 =0,且 =0,即2x1﹣cy1=0,x1﹣cy1+z1=0,
取x1=c,则y1=2,z1=c,即=(c,2,c),
设平面BDE的法向量为=(x2,y2,z2,由 =0, =0,可得﹣x2=0,x2﹣cy2+z2=0,
可令z2=c,则y2=,即有=(0,,c),
则cos<,>==,解得c=,
即AB=.
21.已知直角三角形ABC中∠BAC=90°,CA=2AB=4,D,E分别是AC,BC边中点,将△CDE和△BAE分别沿着DE,AE翻折,形成三棱锥P﹣ADE,M是AD中点.
(1)证明:PM⊥平面ADE;
(2)若直线PM上存在一点Q,使得QE与平面PAE所成角的正弦值为,求QM的值.
(1)证明:由题意知,PA=BA=2,PD=CD=CA=2,
所以PA=PD=2,
又M为AD中点,所以PM⊥AD,
因为D,E分别是AC,BC边中点,所以DE∥AB,
因为∠BAC=90°,所以DE⊥AD,DE⊥CD,即DE⊥PD,
因为AD∩PD=D,AD、PD 平面PAD,所以DE⊥平面PAD,
又PM 平面PAD,所以PM⊥DE,
因为AD∩DE=D,AD、DE 平面ADE,
所以PM⊥平面ADE.
(2)解:以M为坐标原点,MD,MP分别为x,z轴,作My∥DE,建立如图所示的空间直角坐标系,
由PD=2,PA=2,DE=AB=1,
得A(﹣1,0,0),D(1,0,0),P(0,0,),E(1,1,0),
所以=(﹣1,0,﹣),=(2,1,0),
设平面PAE的法向量为=(x,y,z),则,即,
令z=﹣1,则x=,y=﹣2,所以=(,﹣2,﹣1),
设Q(0,0,t),则,
因为QE与平面PAE所成角的正弦值为,所以,解得,
所以Q(0,0,),
故.
22.如图,在四棱锥P﹣ABCD中,已知底面ABCD是正方形,PC⊥底面ABCD,且PC=BC=1,E是棱PB上一点.
(1)若PD∥平面ACE,证明:E是PB的中点;
(2)线段PB上是否存在点E,使二面角P﹣AC﹣E的余弦值是?若存在,求的值;若不存在,请说明理由.
解:(1)证明:如图,连接BD交AC于点O,连接EO,
∵ABCD是正方形,∴O是BD的中点,
又PD∥平面ACE,PD 平面PBD,平面PBD∩平面ACE=EO,
∴PD∥EO,
∵O为BD的中点,∴E是PB的中点;
(2)以C为坐标原点,建立如图所示的空间直角坐标系,
则C(0,0,0),A(1,1,0),B(1,0,0),D(0,1,0),P(0,0,1),
设(0<λ<1),设E(a,b,c),
∴,,,则a=λ,b=0,c=1﹣λ,
则E(λ,0,1﹣λ),,,
由BD⊥AC且BD⊥PC,可知是平面PAC的一个法向量.
设为平面EAC的法向量,
则,即,取,
∴,
解得,即.
