导数参数问题
图片预览











文档简介
课件35张PPT。 三河二中 崔宝明导数及其应用
----求参数问题教学目标
知识点:
(1)熟记基本导数公式,掌握两个函数和、差、积、商的求导法则
(2)学会求函数的单调区间、极值和最值中的参数问题.
(3)导数在恒成立问题中求参数的作用.
重点:
能利用导数研究函数的单调性、极值、最值,会求函数的单调区间、极值和最值中的参数问题.
难点:
导数在求函数的单调区间、极值、最值、证明中的应用及恒成立问题中的求参数的作用.
能力点:
培养学生的数形结合、转化、分类讨论的数学思想,提高发现问题、分析问题、解决问题的能力.
考点:
1.导数的概念、四则运算、常用函数的导数的考查
2.利用导数求函数的单调区间、极值、最值.
3.会求函数的单调区间、极值和最值中的参数问题.
易错易混点:
使导函数等于零的点当成了是极值点,没有进一步的检验,在选择题、和填空题中经常出错.1.基本初等函数的导数公式
(1)若f(x)=c,则f′(x)=0;
(2)若f(x)= (n∈Q*),则f′(x)=_____;
(3)若f(x)=sinx,则f′(x)=_____;
(4)若f(x)=cosx,则f′(x)=______;
(5)若f(x)=ax,则f′(x)=_____(a>0);
(6)若f(x)=ex,则f′(x)=__;
(7)若f(x)=logax,则f′(x)= (a>0且a≠1);
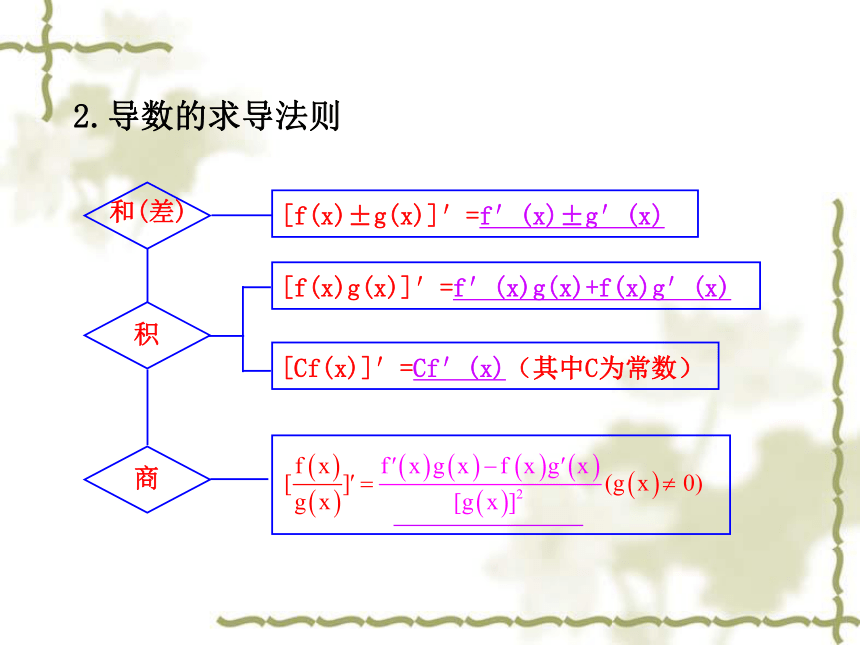
(8)若f(x)=lnx,则f′(x)= .cosx-sinxaxlnaex基础知识回顾 2.导数的求导法则[f(x)±g(x)]′=f′(x)±g′(x)[Cf(x)]′=Cf′(x)(其中C为常数)[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)利用积(或商)的导数运算法则时,注意避免以下错误:
①[f(x)g(x)]′=f′(x)g′(x);
②[ ]′=
③[ ]′=温馨提示:利用导数几何意义求参数 类型一【典例训练】体验高考主干知识【典例训练】
1.若函数f(x)=ax3-x2+x-5在R上单调递增,则实数a的取值范围为________.
2.已知函数f(x)=2ax- ,x∈(0,1].若f(x)在(0,1]上是增函数,求a的取值范围.已知函数单调性求参数范围类型二【解析】1.方法一:
∵f′(x)=3ax2-2x+1,
∴由题意f(x)=ax3-x2+x-5在R上单调递增,可知
3ax2-2x+1≥0对x∈R恒成立.
a=0时,-2x+1≥0不能恒成立,
∴
解得a≥ .方法二:∵f′(x)=3ax2-2x+1.
∴由题意f(x)=ax3-x2+x-5在R上单调递增,可知
3ax2-2x+1≥0对x∈R恒成立.
∴当x=0时,1≥0恒成立,
∴a∈R.
当x≠0时,3ax2-2x+1≥0转化为
a≥
即a≥ 对x∈R恒成立.令 =t(t≠0),则a≥ 对t≠0恒成立.
∵y= (t≠0)的最大值为 .
∴a≥ .
综上,a≥ .
答案:a≥ 【想一想】
(1)解答题1由题意仅得f′(x)>0可以吗?
(2)二次函数3ax2-2x+1≥0恒成立的实质是什么?
提示:(1)由函数单调递增仅得f′(x)>0是不够的,即也可能f′(x)=0,对于能否取到等号的问题,通常需要单独验证.
(2)二次函数3ax2-2x+1≥0恒成立的实质是二次函数图象开口向上,且与x轴至多有一个交点.解题流程∵f(x)在(0,1]上是增函数,
∴f′(x)≥0在(0,1]上恒成立∵f(x)=2ax- ∴f′(x)=2a+2.已知函数f(x)=2ax- ,x∈(0,1].若f(x)在(0,1]上是增函数,
求a的取值范围.∵g(x)=- 在(0,1]上是增函数,
∴g(x)max=g(1)=-1∴a≥-1,即a的取值范围为[-1,+ )【变式训练】已知函数f(x)=x2+ (x≠0,a∈R),若f(x)在[2,+∞)上是增函数,求a的取值范围.
【解析】∵f′(x)=2x- 且f(x)在[2,+∞)上是增函数,
∴f′(x)≥0即 ≥0对x∈[2,+∞)恒成立.
∵x2>0,∴2x3-a≥0对x∈[2,+∞)恒成立.
即a≤2x3对x∈[2,+∞)恒成立.
∵y=2x3在[2,+∞)上是增函数,∴ymin=16,∴a≤16.【解析】1.f′(x)=3x2+2ax+b,依题意得
即 解得 或
但由于当a=-3,b=3时,f′(x)=3x2-6x+3≥0,故f(x)在R上单调递增,不可能在x=1处取得极值,
∴ 不合题意,舍去;而当 时,经检验知,符合题意,故a,b的值分别为4,-11.
答案:4 -11【典例训练】
例题:若函数f(x)=x3+ax2+bx+a2在x=1处取得极值10,则a=_____,b=_____.已知函数的极值求参数类型三 【技法点拨】
已知函数极值点或极值求参数的两个注意点
(1)常根据极值点处导数为0和极值的两个条件列方程组,利用待定系数法求解.
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.【典例训练】
例题:若f(x)=ax3-6ax2+b(a>0),x∈[-1,2]的最大值为3,最小值为-29,求a,b的值.已知函数最值问题求参数类型四【解析】f′(x)=3ax2-12ax=3ax(x-4).
令f′(x)=0,得x=0或x=4.
∵x∈[-1,2],∴x=0.
∵a>0,
∴当x变化时,f′(x)及f(x)的变化情况如下表:∴当x=0时,f(x)取极大值,即最大值为3,∴b=3.
又f(2)=8a-24a+3=-16a+3,
f(-1)=-7a+3>f(2),
∴当x=2时,f(x)取最小值,为-16a+3=-29,
∴a=2.∴a=2,b=3. 【想一想】
为什么对a的符号加以限定?
提示:通过解答可知,a的符号对函数的单调性的变化有直接的影响,进而导致函数的最值也受a的符号的影响,如果题不对a的符号限定,应注意对a进行讨论. 题中a>0这一条件删去,其他条件不变,求a,b的值.
【解析】显然a≠0(否则f(x)=b为常函数,矛盾).
则f′(x)=3ax2-12ax=3ax(x-4).
令f′(x)=0,得x=0或x=4.
∵x∈[-1,2],∴x=0.
∴(1)当a>0时,【讨论探究】则当x变化时,f′(x)及f(x)的变化情况如下表:
∴当x=0时,f(x)取极大值,即最大值为3,∴b=3.
又f(2)=8a-24a+3=-16a+3,
f(-1)=-7a+3>f(2),
∴当x=2时,f(x)取最小值,为-16a+3=-29,
∴a=2.∴a=2,b=3.(2)当a<0时,
则当x变化时,f′(x)及f(x)的变化情况如下表:
∴当x=0时,f(x)取极小值,即最小值为-29,
∴b=-29.
又f(2)=8a-24a-29=-16a-29,
f(-1)=-7a-29<f(2),∴当x=2时,f(x)取最大值,为-16a-29=3,
∴a=-2.
∴a=-2,b=-29.
综上所述,a=2,b=3或a=-2,b=-29.体验高考主干知识
函数的极值与最值
关键词:极值、最值、参数影响下的极值与最值【技法点拨】
已知函数的最大值或最小值,也可利用导数,采用待定系数法,列出字母系数的方程或方程组,解出字母系数,从而求出函数的解析式,进而可以研究函数的其他性质.【典例训练】
已知f(x)=x3- x2-2x+5,当x∈[-1,2]时,f(x)<a恒成立,求实数a的取值范围.有关恒成立问题求参数类型五【解析】 ∵f(x)=x3- x2-2x+5,
∴f′(x)=3x2-x-2.
令f′(x)=0,即3x2-x-2=0,
∴x=1或x=- .
当x变化时,f′(x)及f(x)的变化情况如下表: +0-0+↗↘↗∴当x=- 时,f(x)取得极大值f(- )=
当x=1时,f(x)取得极小值f(1)=
又f(-1)= f(2)=7,
∴f(x)在x∈[-1,2]上的最大值为f(2)=7.
∴要使f(x)<a恒成立,需f(x)max<a,即a>7.
∴所求实数a的取值范围是(7,+∞).在确定a的取值范围时,要注意等号能否取到.【互动探究】题中,把“f(x)<a”改为“f(x)≥a”,求实数a的取值范围.
【解题指南】解答本题可利用导数求出函数f(x)的最小值,进而可得a的取值范围.
【解析】由本题解析可知
f(2)=7,
∴f(x)在x∈[-1,2]上的最小值为f(1)= ,
∴要使f(x)≥a恒成立,需f(x)min≥a,即a≤ ,
∴所求实数a的取值范围是(-∞, ].【技法点拨】
不等式恒成立问题常用的解题方法分离参数,转化为f(x)≥a恒成立,即f(x)min≥a;或f(x)≤a恒成立,即f(x)max≤a求f(x)min或f(x)max写出参数的取值范围课堂小结:布置作业:练习册第79页 专题练习求参数的方法:1、待定系数法
2、数形结合法
3、分离参数法反馈练习:(见学案)学生学习收获展示台 班级 姓名
----求参数问题教学目标
知识点:
(1)熟记基本导数公式,掌握两个函数和、差、积、商的求导法则
(2)学会求函数的单调区间、极值和最值中的参数问题.
(3)导数在恒成立问题中求参数的作用.
重点:
能利用导数研究函数的单调性、极值、最值,会求函数的单调区间、极值和最值中的参数问题.
难点:
导数在求函数的单调区间、极值、最值、证明中的应用及恒成立问题中的求参数的作用.
能力点:
培养学生的数形结合、转化、分类讨论的数学思想,提高发现问题、分析问题、解决问题的能力.
考点:
1.导数的概念、四则运算、常用函数的导数的考查
2.利用导数求函数的单调区间、极值、最值.
3.会求函数的单调区间、极值和最值中的参数问题.
易错易混点:
使导函数等于零的点当成了是极值点,没有进一步的检验,在选择题、和填空题中经常出错.1.基本初等函数的导数公式
(1)若f(x)=c,则f′(x)=0;
(2)若f(x)= (n∈Q*),则f′(x)=_____;
(3)若f(x)=sinx,则f′(x)=_____;
(4)若f(x)=cosx,则f′(x)=______;
(5)若f(x)=ax,则f′(x)=_____(a>0);
(6)若f(x)=ex,则f′(x)=__;
(7)若f(x)=logax,则f′(x)= (a>0且a≠1);
(8)若f(x)=lnx,则f′(x)= .cosx-sinxaxlnaex基础知识回顾 2.导数的求导法则[f(x)±g(x)]′=f′(x)±g′(x)[Cf(x)]′=Cf′(x)(其中C为常数)[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)利用积(或商)的导数运算法则时,注意避免以下错误:
①[f(x)g(x)]′=f′(x)g′(x);
②[ ]′=
③[ ]′=温馨提示:利用导数几何意义求参数 类型一【典例训练】体验高考主干知识【典例训练】
1.若函数f(x)=ax3-x2+x-5在R上单调递增,则实数a的取值范围为________.
2.已知函数f(x)=2ax- ,x∈(0,1].若f(x)在(0,1]上是增函数,求a的取值范围.已知函数单调性求参数范围类型二【解析】1.方法一:
∵f′(x)=3ax2-2x+1,
∴由题意f(x)=ax3-x2+x-5在R上单调递增,可知
3ax2-2x+1≥0对x∈R恒成立.
a=0时,-2x+1≥0不能恒成立,
∴
解得a≥ .方法二:∵f′(x)=3ax2-2x+1.
∴由题意f(x)=ax3-x2+x-5在R上单调递增,可知
3ax2-2x+1≥0对x∈R恒成立.
∴当x=0时,1≥0恒成立,
∴a∈R.
当x≠0时,3ax2-2x+1≥0转化为
a≥
即a≥ 对x∈R恒成立.令 =t(t≠0),则a≥ 对t≠0恒成立.
∵y= (t≠0)的最大值为 .
∴a≥ .
综上,a≥ .
答案:a≥ 【想一想】
(1)解答题1由题意仅得f′(x)>0可以吗?
(2)二次函数3ax2-2x+1≥0恒成立的实质是什么?
提示:(1)由函数单调递增仅得f′(x)>0是不够的,即也可能f′(x)=0,对于能否取到等号的问题,通常需要单独验证.
(2)二次函数3ax2-2x+1≥0恒成立的实质是二次函数图象开口向上,且与x轴至多有一个交点.解题流程∵f(x)在(0,1]上是增函数,
∴f′(x)≥0在(0,1]上恒成立∵f(x)=2ax- ∴f′(x)=2a+2.已知函数f(x)=2ax- ,x∈(0,1].若f(x)在(0,1]上是增函数,
求a的取值范围.∵g(x)=- 在(0,1]上是增函数,
∴g(x)max=g(1)=-1∴a≥-1,即a的取值范围为[-1,+ )【变式训练】已知函数f(x)=x2+ (x≠0,a∈R),若f(x)在[2,+∞)上是增函数,求a的取值范围.
【解析】∵f′(x)=2x- 且f(x)在[2,+∞)上是增函数,
∴f′(x)≥0即 ≥0对x∈[2,+∞)恒成立.
∵x2>0,∴2x3-a≥0对x∈[2,+∞)恒成立.
即a≤2x3对x∈[2,+∞)恒成立.
∵y=2x3在[2,+∞)上是增函数,∴ymin=16,∴a≤16.【解析】1.f′(x)=3x2+2ax+b,依题意得
即 解得 或
但由于当a=-3,b=3时,f′(x)=3x2-6x+3≥0,故f(x)在R上单调递增,不可能在x=1处取得极值,
∴ 不合题意,舍去;而当 时,经检验知,符合题意,故a,b的值分别为4,-11.
答案:4 -11【典例训练】
例题:若函数f(x)=x3+ax2+bx+a2在x=1处取得极值10,则a=_____,b=_____.已知函数的极值求参数类型三 【技法点拨】
已知函数极值点或极值求参数的两个注意点
(1)常根据极值点处导数为0和极值的两个条件列方程组,利用待定系数法求解.
(2)因为导数值等于零不是此点为极值点的充要条件,所以利用待定系数法求解后必须验证根的合理性.【典例训练】
例题:若f(x)=ax3-6ax2+b(a>0),x∈[-1,2]的最大值为3,最小值为-29,求a,b的值.已知函数最值问题求参数类型四【解析】f′(x)=3ax2-12ax=3ax(x-4).
令f′(x)=0,得x=0或x=4.
∵x∈[-1,2],∴x=0.
∵a>0,
∴当x变化时,f′(x)及f(x)的变化情况如下表:∴当x=0时,f(x)取极大值,即最大值为3,∴b=3.
又f(2)=8a-24a+3=-16a+3,
f(-1)=-7a+3>f(2),
∴当x=2时,f(x)取最小值,为-16a+3=-29,
∴a=2.∴a=2,b=3. 【想一想】
为什么对a的符号加以限定?
提示:通过解答可知,a的符号对函数的单调性的变化有直接的影响,进而导致函数的最值也受a的符号的影响,如果题不对a的符号限定,应注意对a进行讨论. 题中a>0这一条件删去,其他条件不变,求a,b的值.
【解析】显然a≠0(否则f(x)=b为常函数,矛盾).
则f′(x)=3ax2-12ax=3ax(x-4).
令f′(x)=0,得x=0或x=4.
∵x∈[-1,2],∴x=0.
∴(1)当a>0时,【讨论探究】则当x变化时,f′(x)及f(x)的变化情况如下表:
∴当x=0时,f(x)取极大值,即最大值为3,∴b=3.
又f(2)=8a-24a+3=-16a+3,
f(-1)=-7a+3>f(2),
∴当x=2时,f(x)取最小值,为-16a+3=-29,
∴a=2.∴a=2,b=3.(2)当a<0时,
则当x变化时,f′(x)及f(x)的变化情况如下表:
∴当x=0时,f(x)取极小值,即最小值为-29,
∴b=-29.
又f(2)=8a-24a-29=-16a-29,
f(-1)=-7a-29<f(2),∴当x=2时,f(x)取最大值,为-16a-29=3,
∴a=-2.
∴a=-2,b=-29.
综上所述,a=2,b=3或a=-2,b=-29.体验高考主干知识
函数的极值与最值
关键词:极值、最值、参数影响下的极值与最值【技法点拨】
已知函数的最大值或最小值,也可利用导数,采用待定系数法,列出字母系数的方程或方程组,解出字母系数,从而求出函数的解析式,进而可以研究函数的其他性质.【典例训练】
已知f(x)=x3- x2-2x+5,当x∈[-1,2]时,f(x)<a恒成立,求实数a的取值范围.有关恒成立问题求参数类型五【解析】 ∵f(x)=x3- x2-2x+5,
∴f′(x)=3x2-x-2.
令f′(x)=0,即3x2-x-2=0,
∴x=1或x=- .
当x变化时,f′(x)及f(x)的变化情况如下表: +0-0+↗↘↗∴当x=- 时,f(x)取得极大值f(- )=
当x=1时,f(x)取得极小值f(1)=
又f(-1)= f(2)=7,
∴f(x)在x∈[-1,2]上的最大值为f(2)=7.
∴要使f(x)<a恒成立,需f(x)max<a,即a>7.
∴所求实数a的取值范围是(7,+∞).在确定a的取值范围时,要注意等号能否取到.【互动探究】题中,把“f(x)<a”改为“f(x)≥a”,求实数a的取值范围.
【解题指南】解答本题可利用导数求出函数f(x)的最小值,进而可得a的取值范围.
【解析】由本题解析可知
f(2)=7,
∴f(x)在x∈[-1,2]上的最小值为f(1)= ,
∴要使f(x)≥a恒成立,需f(x)min≥a,即a≤ ,
∴所求实数a的取值范围是(-∞, ].【技法点拨】
不等式恒成立问题常用的解题方法分离参数,转化为f(x)≥a恒成立,即f(x)min≥a;或f(x)≤a恒成立,即f(x)max≤a求f(x)min或f(x)max写出参数的取值范围课堂小结:布置作业:练习册第79页 专题练习求参数的方法:1、待定系数法
2、数形结合法
3、分离参数法反馈练习:(见学案)学生学习收获展示台 班级 姓名
