【核心素养目标】1.1.3等腰三角形 教学设计
文档属性
| 名称 | 【核心素养目标】1.1.3等腰三角形 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 912.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.1.3等腰三角形教学设计
课题 1.1.3等腰三角形 单元 1 学科 数学 年级 八
教材分析 本节课是等腰三角形的第三课时,通过前面两课时的学习,学生已经掌握了等腰三角形的相关性质,并知道了用综合法证明命题的基本要求和步骤。为学习等腰三角形的判定定理奠定了知识和方法的基础。
核心素养分析 培养学生对命题抽象概括能力,加强发散思维训练。培养大胆分析,敢于求异,勇于探索的精神和能力,形成良好的思维品质。通过对等腰三角形的判定定理的探索,让学生体会探索学习的乐趣,并通过等腰三角形的判定定理的简单应用,加深对定理的理解,从而培养学生利用已有知识解决实际问题的能力。
学习 目标 1.探索等腰三角形判定定理. 2.理解等腰三角形的判定定理,并会运用其进行简单的证明. 3.了解反证法的基本证明思路,并能简单应用。
重点 等腰三角形的判定方法及应用。
难点 探索证明等腰三角形判定定理的思路与方法,掌握证明的基本要求和方法.
教学过程
教学环节 教师活动 学生活动 设计意图
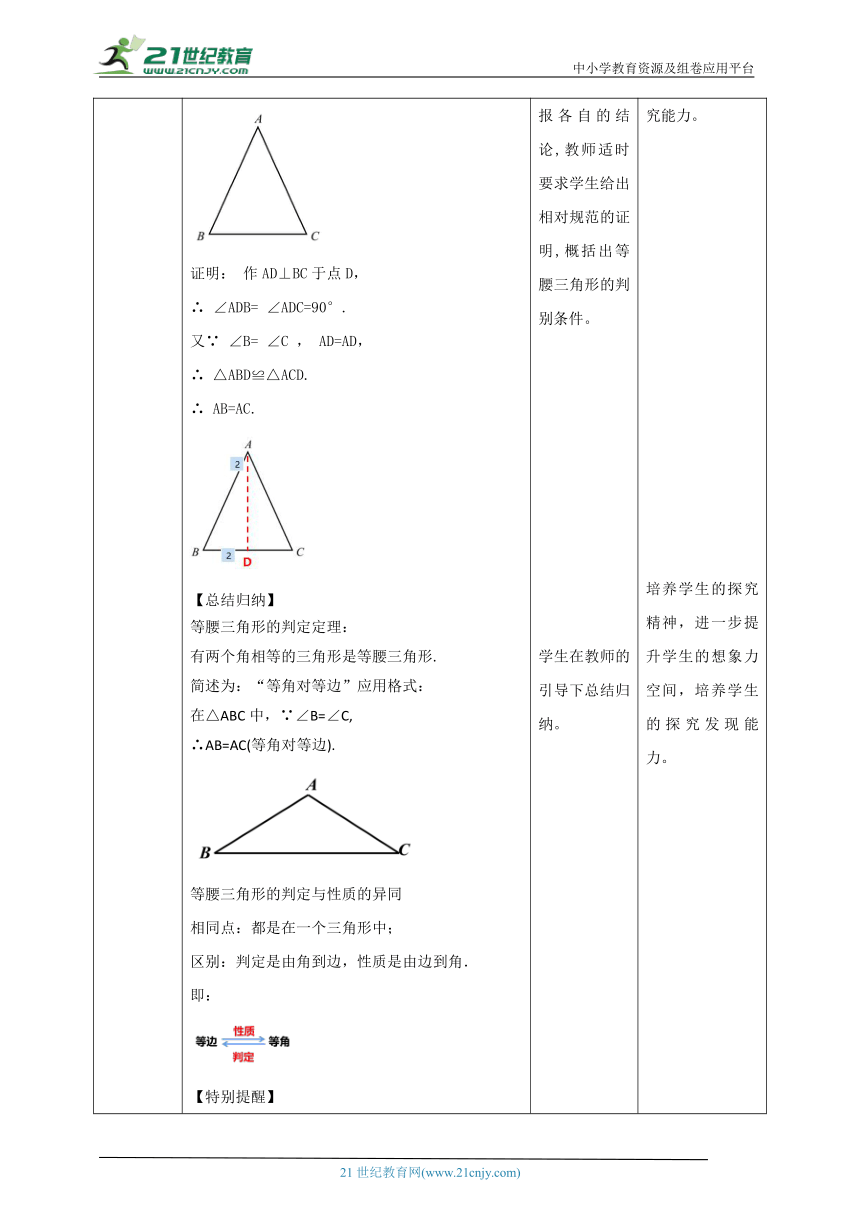
导入新课 1、等腰三角形是怎样定义的? 2、等腰三角形有哪些性质? 在前两节课,我们学习了等腰三角形的相关性质. 怎样的一个三角形才是等腰三角形呢? 教师回顾前面等腰三角形的性质和判定定理的基础上,直接提出问题:如何判别一个三角形是等腰三角形呢 从而引入新课。 回顾等腰三角形的性质,既为后续研究判定提供了基础;同时,直接提出新的问题,过渡自然,引入本课研究内容
讲授新课 我们知道,如果一个三角形有两条边相等,那么它们所对的角相等。反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系? 证明:有两个角相等的三角形是等腰三角形. 已知:如图,在△ABC 中, ∠B= ∠C. 求证:AB=AC . 证明: 作AD⊥BC于点D, ∴ ∠ADB= ∠ADC=90°. 又∵ ∠B= ∠C , AD=AD, ∴ △ABD≌△ACD. ∴ AB=AC. 【总结归纳】 等腰三角形的判定定理: 有两个角相等的三角形是等腰三角形. 简述为:“等角对等边”应用格式: 在△ABC中,∵∠B=∠C, ∴AB=AC(等角对等边). 等腰三角形的判定与性质的异同 相同点:都是在一个三角形中; 区别:判定是由角到边,性质是由边到角. 即: 【特别提醒】 “等角对等边”不能叙述为“如果一个三角形有两个底角相等,那么它的两条腰相等”,因为在未判定出它是等腰三角形之前,不能用“底角”“顶角”“腰”“底边”这些名词. “ 等角对等边”是我们以后证明两条线段相等的常用方法,在证明过程中,经常通过计算三角形各角的度数,或利用角的关系得到角相等,从而得到所对的边相等. 典例精析 【例2】已知:如图,AB= DC,BD=CA. 求证:△AED 是等腰三角形. 证明: ∵ AB=DC, BD=CA, AD=DA, ∴ △ABD≌△DCA(SSS), ∴ ∠ADB= ∠DAC(全等三角形的对应角相等) . ∴ AE=DE (等角对等边). ∴ △AED 是等腰三角形. 【想一想】在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等. 你能证明这个结论吗? 在△ABC 中, 如果 ∠B≠∠C,那么AB≠AC. 证明:在△ABC 中, 已知∠B≠∠C,此时AB与AC要么相等,要么不相等. 假设AB=AC,那么根据“等边对等角”定理可得∠B=∠C,这与已知条件∠B≠∠C相矛盾,因此AB≠AC. 证明时,先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为反证法. 你能总结反证法的证明步骤吗? 反证法的证明步骤: (1)反设:假设命题结论不成立,即假设结论的反面成立. (2)归谬:从这个命题出发,经过推理证明得出矛盾. (3)结论:由矛盾判断假设不成立,从而肯定命题的结论正确. 例3 用反证法证明:一个三角形中不能有两个角是直角. 已知:△ABC. 求证:∠A,∠B,∠C 中不能有两个角是直角. 证明: 假设∠A,∠B, ∠C 中有两个角是直角, 不妨设∠A=∠B=90°, 则∠A+∠B +∠C=90 °+90°+∠C=180 °+∠C >180°. 这与三角形内角和定理矛盾,所以∠A=∠B=90°不成立.所以一个三角形中不能有两个角是直角. 学生自主探究三角形成为等腰三角形的条件,并交流汇报各自的结论,教师适时要求学生给出相对规范的证明,概括出等腰三角形的判别条件。 学生在教师的引导下总结归纳。 通过所学知识做练习,整理步骤,加深印象。 学生思考回答问题,尝试证明问题。 学生在教师的引导下总结归纳。 学生做例题。 经历定理的探究过程,即明确有关定理,同时提高学生的自主探究能力。 培养学生的探究精神,进一步提升学生的想象力空间,培养学生的探究发现能力。 培养学生应用所学知识解决问题的能力与意识,鼓励创新与多角度多方法思考问题,活跃学生的思维,发展创造性. 总结回顾学习内容,帮助学生归纳.巩固学生的所学知识,总结反思。 培养学生应用所学知识解决问题的能力与意识,鼓励创新与多角度多方法思考问题,活跃学生的思维,发展创造性.
课堂练习 1.已知△ABC三个内角的对边分别为a,b,c,则下列条件中,△ABC不是等腰三角形的是( ) A. a=3,b=3,c=4 B. a∶b∶c=4∶5∶6 C. ∠B=50°,∠C=80° D. ∠A∶∠B∶∠C=1∶1∶2 2.用反证法证明“一个三角形中至多有一个钝角”时,应假设( ) A.一个三角形中至少有两个钝角 B.一个三角形中至多有一个钝角 C.一个三角形中至少有一个钝角 D.一个三角形中没有钝角 3、用反证法证明命题“等腰三角形的两底角是锐角”时,第一步为_________________________. 4、如图,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD= . 5.如图,在△ABC 中,∠ABC的平分线交 AC于点 D,DE∥BC. 求证:△EBD是等腰三角形. 6.如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,求证:∠DAB是一个锐角. 学生定时训练,自主解答,老师订正 通过练习调动学生学习的积极性,使学生思维处于积极状态,达到了培养学生思维的灵活性和创造性,解决问题的目的。
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 1.1.3 等腰三角形 1.等腰三角形的判定定理 2.反证法
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.1.3等腰三角形教学设计
课题 1.1.3等腰三角形 单元 1 学科 数学 年级 八
教材分析 本节课是等腰三角形的第三课时,通过前面两课时的学习,学生已经掌握了等腰三角形的相关性质,并知道了用综合法证明命题的基本要求和步骤。为学习等腰三角形的判定定理奠定了知识和方法的基础。
核心素养分析 培养学生对命题抽象概括能力,加强发散思维训练。培养大胆分析,敢于求异,勇于探索的精神和能力,形成良好的思维品质。通过对等腰三角形的判定定理的探索,让学生体会探索学习的乐趣,并通过等腰三角形的判定定理的简单应用,加深对定理的理解,从而培养学生利用已有知识解决实际问题的能力。
学习 目标 1.探索等腰三角形判定定理. 2.理解等腰三角形的判定定理,并会运用其进行简单的证明. 3.了解反证法的基本证明思路,并能简单应用。
重点 等腰三角形的判定方法及应用。
难点 探索证明等腰三角形判定定理的思路与方法,掌握证明的基本要求和方法.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 1、等腰三角形是怎样定义的? 2、等腰三角形有哪些性质? 在前两节课,我们学习了等腰三角形的相关性质. 怎样的一个三角形才是等腰三角形呢? 教师回顾前面等腰三角形的性质和判定定理的基础上,直接提出问题:如何判别一个三角形是等腰三角形呢 从而引入新课。 回顾等腰三角形的性质,既为后续研究判定提供了基础;同时,直接提出新的问题,过渡自然,引入本课研究内容
讲授新课 我们知道,如果一个三角形有两条边相等,那么它们所对的角相等。反过来,如果一个三角形有两个角相等,那么它们所对的边有什么关系? 证明:有两个角相等的三角形是等腰三角形. 已知:如图,在△ABC 中, ∠B= ∠C. 求证:AB=AC . 证明: 作AD⊥BC于点D, ∴ ∠ADB= ∠ADC=90°. 又∵ ∠B= ∠C , AD=AD, ∴ △ABD≌△ACD. ∴ AB=AC. 【总结归纳】 等腰三角形的判定定理: 有两个角相等的三角形是等腰三角形. 简述为:“等角对等边”应用格式: 在△ABC中,∵∠B=∠C, ∴AB=AC(等角对等边). 等腰三角形的判定与性质的异同 相同点:都是在一个三角形中; 区别:判定是由角到边,性质是由边到角. 即: 【特别提醒】 “等角对等边”不能叙述为“如果一个三角形有两个底角相等,那么它的两条腰相等”,因为在未判定出它是等腰三角形之前,不能用“底角”“顶角”“腰”“底边”这些名词. “ 等角对等边”是我们以后证明两条线段相等的常用方法,在证明过程中,经常通过计算三角形各角的度数,或利用角的关系得到角相等,从而得到所对的边相等. 典例精析 【例2】已知:如图,AB= DC,BD=CA. 求证:△AED 是等腰三角形. 证明: ∵ AB=DC, BD=CA, AD=DA, ∴ △ABD≌△DCA(SSS), ∴ ∠ADB= ∠DAC(全等三角形的对应角相等) . ∴ AE=DE (等角对等边). ∴ △AED 是等腰三角形. 【想一想】在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等. 你能证明这个结论吗? 在△ABC 中, 如果 ∠B≠∠C,那么AB≠AC. 证明:在△ABC 中, 已知∠B≠∠C,此时AB与AC要么相等,要么不相等. 假设AB=AC,那么根据“等边对等角”定理可得∠B=∠C,这与已知条件∠B≠∠C相矛盾,因此AB≠AC. 证明时,先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立.这种证明方法称为反证法. 你能总结反证法的证明步骤吗? 反证法的证明步骤: (1)反设:假设命题结论不成立,即假设结论的反面成立. (2)归谬:从这个命题出发,经过推理证明得出矛盾. (3)结论:由矛盾判断假设不成立,从而肯定命题的结论正确. 例3 用反证法证明:一个三角形中不能有两个角是直角. 已知:△ABC. 求证:∠A,∠B,∠C 中不能有两个角是直角. 证明: 假设∠A,∠B, ∠C 中有两个角是直角, 不妨设∠A=∠B=90°, 则∠A+∠B +∠C=90 °+90°+∠C=180 °+∠C >180°. 这与三角形内角和定理矛盾,所以∠A=∠B=90°不成立.所以一个三角形中不能有两个角是直角. 学生自主探究三角形成为等腰三角形的条件,并交流汇报各自的结论,教师适时要求学生给出相对规范的证明,概括出等腰三角形的判别条件。 学生在教师的引导下总结归纳。 通过所学知识做练习,整理步骤,加深印象。 学生思考回答问题,尝试证明问题。 学生在教师的引导下总结归纳。 学生做例题。 经历定理的探究过程,即明确有关定理,同时提高学生的自主探究能力。 培养学生的探究精神,进一步提升学生的想象力空间,培养学生的探究发现能力。 培养学生应用所学知识解决问题的能力与意识,鼓励创新与多角度多方法思考问题,活跃学生的思维,发展创造性. 总结回顾学习内容,帮助学生归纳.巩固学生的所学知识,总结反思。 培养学生应用所学知识解决问题的能力与意识,鼓励创新与多角度多方法思考问题,活跃学生的思维,发展创造性.
课堂练习 1.已知△ABC三个内角的对边分别为a,b,c,则下列条件中,△ABC不是等腰三角形的是( ) A. a=3,b=3,c=4 B. a∶b∶c=4∶5∶6 C. ∠B=50°,∠C=80° D. ∠A∶∠B∶∠C=1∶1∶2 2.用反证法证明“一个三角形中至多有一个钝角”时,应假设( ) A.一个三角形中至少有两个钝角 B.一个三角形中至多有一个钝角 C.一个三角形中至少有一个钝角 D.一个三角形中没有钝角 3、用反证法证明命题“等腰三角形的两底角是锐角”时,第一步为_________________________. 4、如图,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD= . 5.如图,在△ABC 中,∠ABC的平分线交 AC于点 D,DE∥BC. 求证:△EBD是等腰三角形. 6.如图,在等腰三角形ABC中,AB=AC,AD是BC边上的高,求证:∠DAB是一个锐角. 学生定时训练,自主解答,老师订正 通过练习调动学生学习的积极性,使学生思维处于积极状态,达到了培养学生思维的灵活性和创造性,解决问题的目的。
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 1.1.3 等腰三角形 1.等腰三角形的判定定理 2.反证法
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
