2022-2023学年北师大版九年级数学下册2.4 二次函数的应用 课后测评(无答案)
文档属性
| 名称 | 2022-2023学年北师大版九年级数学下册2.4 二次函数的应用 课后测评(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 417.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 20:46:16 | ||
图片预览


文档简介
2.4二次函数的应用课后测评
班级:________ 姓名:________
一、单选题(共 10 小题)
1、某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为( )
A.y=(x﹣40)(500﹣10x) B.y=(x﹣40)(10x﹣500)
C.y=(x﹣40)[500﹣10(x﹣50)] D.y=(x﹣40)[500﹣10(50﹣x)]
2、如图,某幢建筑物从2.25米高的窗口用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点离墙1米,离地面3米,则水流下落点离墙的距离是( )
A.2.5米 B.3米 C.3.5米 D.4米
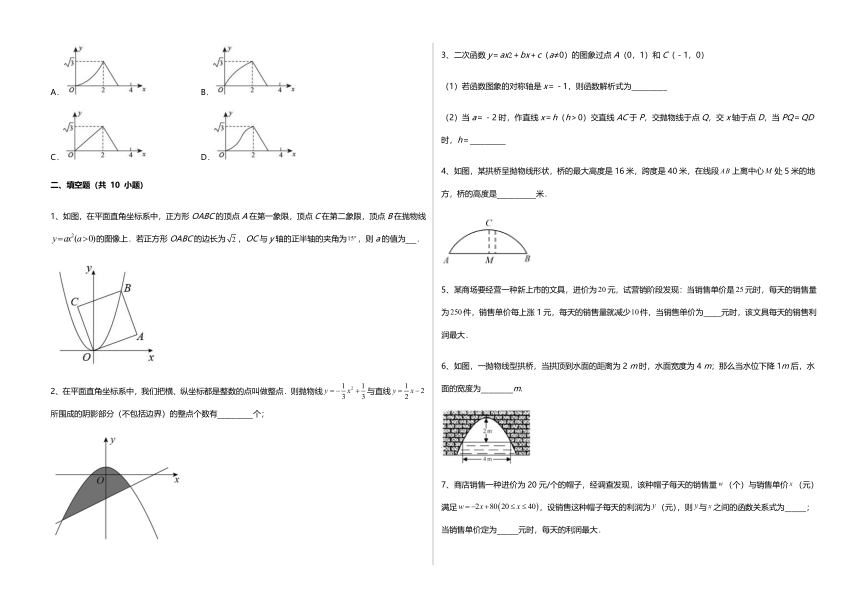
3、如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
4、如图,已知A、B是反比例函数图象上的两点,轴,交x轴于点C.动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C.过点P作轴于Q.设的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
B.
C. D.
5、“星星书店”出售某种笔记本,若每个可获利元,一天可售出个.当一天出售该种文具盒的总利润最大时,的值为( )
A.1 B.2 C.3 D.4
6、如图,二次函数y=﹣x2+2x+m+1的图象交x轴于点A(a,0)和B(b,0),交y轴于点C,图象的顶点为D.下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=4;
③点C关于图象对称轴的对称点为E,点M为x轴上的一个动点,当m=2时,△MCE周长的最小值为2;
④图象上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2,
其中真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
7、如图,中,,,,动点从点出发,沿以每秒2个单位的速度向终点运动(不与,重合),过作,交于点,为中点,连接,设点运动的时间为,则下列说法错误的是( )
A.当时, B.当时,
C.当时, D.当,有面积最大
8、使用家用燃气灶烧开同一壶水所需的燃气量y(单位:)与旋钮的旋转角度x(单位:度)(0°<x≤90°)近似满足函数关系(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.18° B.36° C.41° D.58°
9、某民俗旅游村为接待游客住宿需要,开设了有张床位的旅馆,当每张床位每天收费元时,床位可全部租出.若每张床位每天收费提高元,则相应的减少了张床位租出.如果每张床位每天以元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.14元 B.15元 C.16元 D.18元
10、如图,点P,Q从边长为2的等边三角形的点B出发,分别沿着,两边以相同的速度在的边上运动,当两点在边上运动到重合时停止.在此过程中,设点P,Q移动过程中各自的路程为x,所得的面积为y,则y随x变化的函数图象大致为( )
A. B.
C. D.
二、填空题(共 10 小题)
1、如图,在平面直角坐标系中,正方形OABC的顶点A在第一象限,顶点C在第二象限,顶点B在抛物线的图像上.若正方形OABC的边长为,OC与y轴的正半轴的夹角为,则a的值为___.
2、在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.则抛物线与直线所围成的阴影部分(不包括边界)的整点个数有__________个;
3、二次函数y=ax+bx+c(a≠0)的图象过点A(0,1)和C(-1,0)
(1)若函数图象的对称轴是x=-1,则函数解析式为__________
(2)当a=-2时,作直线x=h(h>0)交直线AC于P,交抛物线于点Q,交x轴于点D,当PQ=QD时,h=__________
4、如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段上离中心处5米的地方,桥的高度是___________米.
5、某商场要经营一种新上市的文具,进价为元,试营销阶段发现:当销售单价是元时,每天的销售量为件,销售单价每上涨1元,每天的销售量就减少件,当销售单价为_____元时,该文具每天的销售利润最大.
6、如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为_________m.
7、商店销售一种进价为20元/个的帽子,经调查发现,该种帽子每天的销售量(个)与销售单价(元)满足,设销售这种帽子每天的利润为(元),则与之间的函数关系式为______;当销售单价定为______元时,每天的利润最大.
8、已知二次函数y=2x2﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有P1,P2,P3三点满足S△ABP1=S△ABP2=S△ABP3=m,则m的值为______.
9、如图,一次足球训练中,一球员从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,当足球下落到离地面米时,足球飞行的水平距离为__________米.
10、如图,有一座抛物线拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m达到警戒水位时,水面CD的宽是10米,建立如图所示的平面直角坐标系,O为坐标原点,如果水位以0.2m/h的速度匀速上涨,那么达到警戒水位后,再过_____h水位达到桥拱最高点O.
三、解答题(共 6 小题)
1、某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?
(3)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
2、在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处.
小聪测量黑球减速后的运动速度(单位:)、运动距离(单位:)随运动时间(单位:)变化的数据,整理得下表.
运动时间 0 1 2 3 4
运动速度 10 9.5 9 8.5 8
运动距离 0 9.75 19 27.75 36
小聪探究发现,黑球的运动速度与运动时间之间成一次函数关系,运动距离与运动时间之间成二次函数关系.
(1)直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围)
(2)当黑球减速后运动距离为时,求它此时的运动速度;
(3)若白球一直以的速度匀速运动,问黑球在运动过程中会不会碰到白球?请说明理由.
3、如图,在平面直角坐标系中,抛物线与x轴交于点A,B,与y轴交于点C,点A和点C的坐标分别为和
(1)求抛物线的函数表达式;
(2)将线段CB绕点C顺时针旋转90°,得到线段CD,连接AD,求线段AD的长;
(3)点M是抛物线上位于第一象限图象上的一动点,连接AM交BC于点N,连接BM,当时,请直接写出点M的横坐标的值.
4、某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运动的轨迹为抛物线,篮圈距地面3m.建立如图所示的平面坐标系,求抛物线的解析式并判断此球能否准确投中?
5、某超市采购了两批同样的冰墩墩挂件,第一批花了6600元,第二批花了8000元,第一批每个挂件的进价是第二批的1.1倍,且第二批比第一批多购进50个.
(1)求第二批每个挂件的进价;
(2)两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少?
6、如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.
(1)求桥拱项部O离水面的距离.
(2)如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x元,月销售利润为y元,则y与x的函数关系式为( )
A.y=(x﹣40)(500﹣10x) B.y=(x﹣40)(10x﹣500)
C.y=(x﹣40)[500﹣10(x﹣50)] D.y=(x﹣40)[500﹣10(50﹣x)]
2、如图,某幢建筑物从2.25米高的窗口用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点离墙1米,离地面3米,则水流下落点离墙的距离是( )
A.2.5米 B.3米 C.3.5米 D.4米
3、如图,有一抛物线形拱桥,当拱顶离水面时,水面宽,当水面宽增加时,则水面应下降的高度是( )
A. B. C. D.
4、如图,已知A、B是反比例函数图象上的两点,轴,交x轴于点C.动点P从坐标原点O出发,沿O→A→B→C匀速运动,终点为C.过点P作轴于Q.设的面积为S,点P运动的时间为t,则S关于t的函数图象大致为( )
B.
C. D.
5、“星星书店”出售某种笔记本,若每个可获利元,一天可售出个.当一天出售该种文具盒的总利润最大时,的值为( )
A.1 B.2 C.3 D.4
6、如图,二次函数y=﹣x2+2x+m+1的图象交x轴于点A(a,0)和B(b,0),交y轴于点C,图象的顶点为D.下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=4;
③点C关于图象对称轴的对称点为E,点M为x轴上的一个动点,当m=2时,△MCE周长的最小值为2;
④图象上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2,
其中真命题的个数有( )
A.1个 B.2个 C.3个 D.4个
7、如图,中,,,,动点从点出发,沿以每秒2个单位的速度向终点运动(不与,重合),过作,交于点,为中点,连接,设点运动的时间为,则下列说法错误的是( )
A.当时, B.当时,
C.当时, D.当,有面积最大
8、使用家用燃气灶烧开同一壶水所需的燃气量y(单位:)与旋钮的旋转角度x(单位:度)(0°<x≤90°)近似满足函数关系(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.18° B.36° C.41° D.58°
9、某民俗旅游村为接待游客住宿需要,开设了有张床位的旅馆,当每张床位每天收费元时,床位可全部租出.若每张床位每天收费提高元,则相应的减少了张床位租出.如果每张床位每天以元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.14元 B.15元 C.16元 D.18元
10、如图,点P,Q从边长为2的等边三角形的点B出发,分别沿着,两边以相同的速度在的边上运动,当两点在边上运动到重合时停止.在此过程中,设点P,Q移动过程中各自的路程为x,所得的面积为y,则y随x变化的函数图象大致为( )
A. B.
C. D.
二、填空题(共 10 小题)
1、如图,在平面直角坐标系中,正方形OABC的顶点A在第一象限,顶点C在第二象限,顶点B在抛物线的图像上.若正方形OABC的边长为,OC与y轴的正半轴的夹角为,则a的值为___.
2、在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.则抛物线与直线所围成的阴影部分(不包括边界)的整点个数有__________个;
3、二次函数y=ax+bx+c(a≠0)的图象过点A(0,1)和C(-1,0)
(1)若函数图象的对称轴是x=-1,则函数解析式为__________
(2)当a=-2时,作直线x=h(h>0)交直线AC于P,交抛物线于点Q,交x轴于点D,当PQ=QD时,h=__________
4、如图,某拱桥呈抛物线形状,桥的最大高度是16米,跨度是40米,在线段上离中心处5米的地方,桥的高度是___________米.
5、某商场要经营一种新上市的文具,进价为元,试营销阶段发现:当销售单价是元时,每天的销售量为件,销售单价每上涨1元,每天的销售量就减少件,当销售单价为_____元时,该文具每天的销售利润最大.
6、如图,一抛物线型拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m;那么当水位下降1m后,水面的宽度为_________m.
7、商店销售一种进价为20元/个的帽子,经调查发现,该种帽子每天的销售量(个)与销售单价(元)满足,设销售这种帽子每天的利润为(元),则与之间的函数关系式为______;当销售单价定为______元时,每天的利润最大.
8、已知二次函数y=2x2﹣8x+6的图象交x轴于A,B两点.若其图象上有且只有P1,P2,P3三点满足S△ABP1=S△ABP2=S△ABP3=m,则m的值为______.
9、如图,一次足球训练中,一球员从球门正前方将球射向球门,球射向球门的路线呈抛物线,当球飞行的水平距离为6米时,球达到最高点,此时球离地面3米,当足球下落到离地面米时,足球飞行的水平距离为__________米.
10、如图,有一座抛物线拱桥,在正常水位时水面AB的宽为20m,如果水位上升3m达到警戒水位时,水面CD的宽是10米,建立如图所示的平面直角坐标系,O为坐标原点,如果水位以0.2m/h的速度匀速上涨,那么达到警戒水位后,再过_____h水位达到桥拱最高点O.
三、解答题(共 6 小题)
1、某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.
(1)求y与x之间的函数关系式.
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?
(3)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?
2、在一条笔直的滑道上有黑、白两个小球同向运动,黑球在处开始减速,此时白球在黑球前面处.
小聪测量黑球减速后的运动速度(单位:)、运动距离(单位:)随运动时间(单位:)变化的数据,整理得下表.
运动时间 0 1 2 3 4
运动速度 10 9.5 9 8.5 8
运动距离 0 9.75 19 27.75 36
小聪探究发现,黑球的运动速度与运动时间之间成一次函数关系,运动距离与运动时间之间成二次函数关系.
(1)直接写出关于的函数解析式和关于的函数解析式(不要求写出自变量的取值范围)
(2)当黑球减速后运动距离为时,求它此时的运动速度;
(3)若白球一直以的速度匀速运动,问黑球在运动过程中会不会碰到白球?请说明理由.
3、如图,在平面直角坐标系中,抛物线与x轴交于点A,B,与y轴交于点C,点A和点C的坐标分别为和
(1)求抛物线的函数表达式;
(2)将线段CB绕点C顺时针旋转90°,得到线段CD,连接AD,求线段AD的长;
(3)点M是抛物线上位于第一象限图象上的一动点,连接AM交BC于点N,连接BM,当时,请直接写出点M的横坐标的值.
4、某校九年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运动的轨迹为抛物线,篮圈距地面3m.建立如图所示的平面坐标系,求抛物线的解析式并判断此球能否准确投中?
5、某超市采购了两批同样的冰墩墩挂件,第一批花了6600元,第二批花了8000元,第一批每个挂件的进价是第二批的1.1倍,且第二批比第一批多购进50个.
(1)求第二批每个挂件的进价;
(2)两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少?
6、如图1是一座抛物线型拱桥侧面示意图.水面宽AB与桥长CD均为24m,在距离D点6米的E处,测得桥面到桥拱的距离EF为1.5m,以桥拱顶点O为原点,桥面为x轴建立平面直角坐标系.
(1)求桥拱项部O离水面的距离.
(2)如图2,桥面上方有3根高度均为4m的支柱CG,OH,DI,过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面距离为1m.
①求出其中一条钢缆抛物线的函数表达式.
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求彩带长度的最小值.
