2022-2023学年京改版九年级数学下册23.3轴对称变换课后同步练习(无答案)
文档属性
| 名称 | 2022-2023学年京改版九年级数学下册23.3轴对称变换课后同步练习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 676.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 00:00:00 | ||
图片预览




文档简介
23.3轴对称变换课后同步练习
班级:________ 姓名:________
一、单选题(共 10 小题)
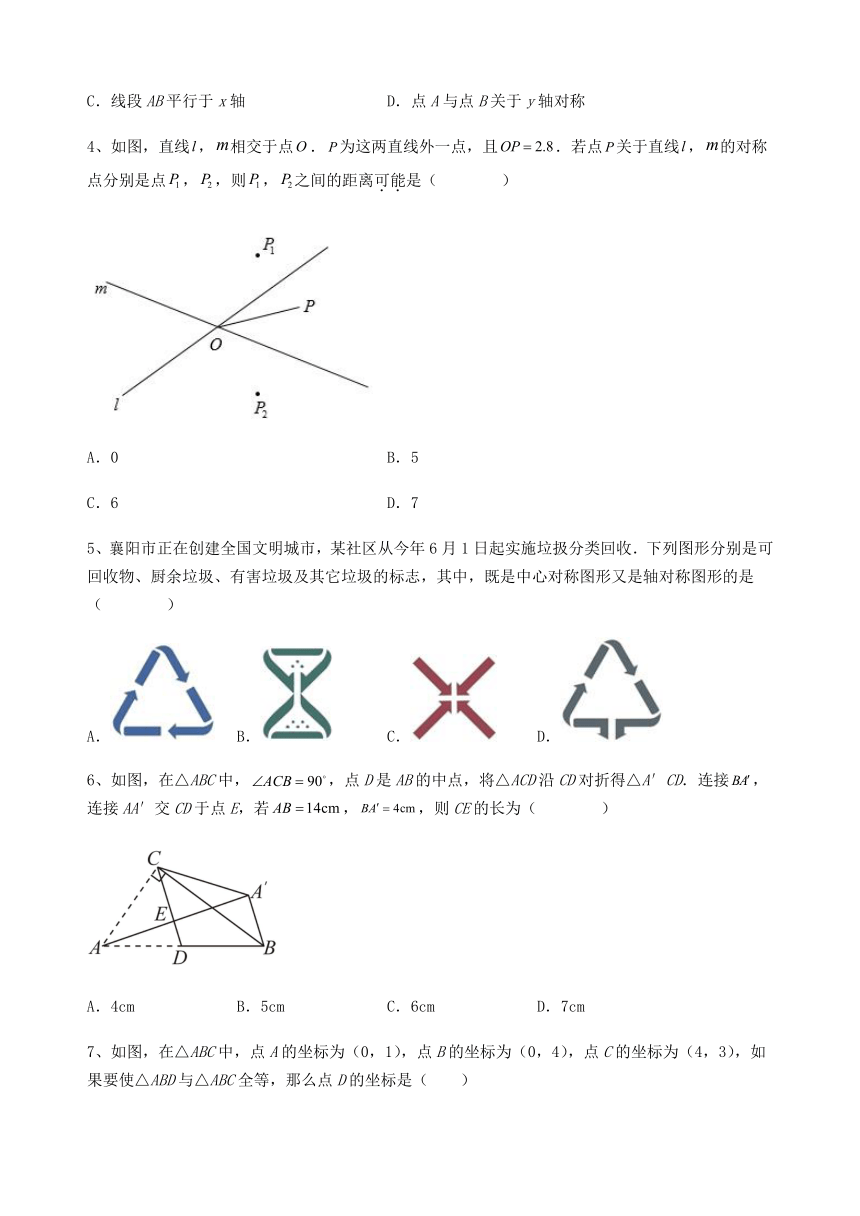
1、如图,将沿AC所在的直线翻折得到,再将沿所在的直线翻折得到,点在同一条直线上,,则( )
A. B. C. D.
2、如图,在△ABC中,点O是∠BAC的平分线与线段AC的垂直平分线的交点,OD⊥AB于点D,OF⊥AC于点F,则下列结论不一定成立的是( )
A.OA=OC B.OD=OF C.OA=OB D.AD=FC
3、在平面直角坐标系中,点A的坐标为(-2,-3),点B的坐标为(3,-3),下列说法不正确的是( )
A.点A在第三象限 B.点B在第二、四象限的角平分线上
C.线段AB平行于x轴 D.点A与点B关于y轴对称
4、如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是( )
A.0 B.5
C.6 D.7
5、襄阳市正在创建全国文明城市,某社区从今年6月1日起实施垃扱分类回收.下列图形分别是可回收物、厨余垃圾、有害垃圾及其它垃圾的标志,其中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
6、如图,在△ABC中,,点D是AB的中点,将△ACD沿CD对折得△A′CD.连接,连接AA′交CD于点E,若,,则CE的长为( )
A.4cm B.5cm C.6cm D.7cm
7、如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是( )
A.(﹣4,3)
B.(﹣4,2)
C.(4,2)或(﹣4,3)
D.(4,2)或(﹣4,2)或(﹣4,3)
8、是点关于x轴的对称点.若一个正比例函数的图象经过点,则该函数的表达式为( )
A. B. C. D.
9、已知点经变换后到点B,下面的说法正确的是( )
A.点A与点B关于x轴对称,则点B的坐标为
B.点A绕原点按顺时针方向旋转90°后到点B,则点B的坐标为
C.点A与点B关于原点中心对称,则点B的坐标为
D.点A先向上平移3个单位,再向右平移4个单位到点B,则点B的坐标为
10、如图,将 ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66° B.104° C.114° D.124°
二、填空题(共 10 小题)
1、如图,在等边△ABC中,AD⊥BC,垂足为点D,AD=4,P是AD上一动点,E为AB的中点,连接PE,PB,则PB+PE的最小值为 ___.
2、在平面直角坐标系中,点A(2,m)在直线上,点A关于y轴对称的点B恰好落在直线上,则k的值为___.
3、如图,和关于直线AB对称,和关于直线AC对称,CD与AE交于点F,若,,则的度数为________.
4、在菱形ABCD中,∠B=60°,BC=2cm,M为AB的中点,N为BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE,CE,当△CDE为等腰三角形时,线段BN的长为_____.
5、如图,在中,将沿直线折叠,使点B落在点D的位置,若,,则的度数是__________.
6、如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,点P2020的坐标是__.
7、把一张边长为8cm的正方形纸片按如图所示的方法对折两次后剪去两个角,打开后得到一个正多边形.
(1)如果打开后得到一个正方形,则这个正方形的边长为______.
(2)有以下5个正多边形:①正五边形;②正六边形;③正八边形;④正十边形;⑤正十二边形,其中打开后可以得到是______.(只填序号)
8、如图,方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有_________ 个.
9、已知点,若点M关于x轴的对称点在第三象限,则a的取值范围是______.
10、如图,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,2),点A与点C(-3,2)之间的距离为 _____,点D在y轴上运动,当AD+BD的值最小时,点D的坐标为 _____,此时AD+BD的最小值为 _____.
三、解答题(共 6 小题)
1、如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1)B(4,2)C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,则这条对称轴是 ,此时C点关于这条直线的对称点C2的坐标为 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上确定一点P,使△APB的周长最小.(注:不写作法,不求坐标,只保留作图痕迹)
2、如图,在平面直角坐标系中,已知
(1)在图中作出ABC关于轴的对称图形;
(2)若将ABC向右平移2个单位得到,则点B的对应点的坐标是______;
(3)求的长及ABC的面积.
3、如图,在正方形网格中,是格点三角形.
(1)画出,使得和关于直线对称;
(2)请在直线上找一点(即画出点),使点到点和点的距离之和最小;
(3)求的面积.
4、如图,三个顶点的坐标分别为
(1)若与关于y轴成轴对称,在图中画出,点坐标为__________;
(2)若直线与y轴相交于点,在y轴上是否存在点Q.使得,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3)在x轴上找一点P,使的值最小,点P的坐标是____________.
5、如图,长方形,点E是上的一点,将沿折叠后得到,且点O在长方形内部.已知,.
(1)如图1,若,求四边形的面积.
(2)如图2,延长交于F,连结,将沿折叠,当点D的对称点恰好为点O时,求四边形的面积.
(3)如图3,在(2)的条件下,延长交于点G,连结,将沿折叠,当点C的对称点恰好为点O时,求四边形的面积.
6、如图,三个顶点的坐标分别是,,.
(1)试画出关于轴对称的,并写出、、的坐标;
(2)在轴上求作一点,使周长最小,试画出,直接写出点的坐标.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、如图,将沿AC所在的直线翻折得到,再将沿所在的直线翻折得到,点在同一条直线上,,则( )
A. B. C. D.
2、如图,在△ABC中,点O是∠BAC的平分线与线段AC的垂直平分线的交点,OD⊥AB于点D,OF⊥AC于点F,则下列结论不一定成立的是( )
A.OA=OC B.OD=OF C.OA=OB D.AD=FC
3、在平面直角坐标系中,点A的坐标为(-2,-3),点B的坐标为(3,-3),下列说法不正确的是( )
A.点A在第三象限 B.点B在第二、四象限的角平分线上
C.线段AB平行于x轴 D.点A与点B关于y轴对称
4、如图,直线,相交于点.为这两直线外一点,且.若点关于直线,的对称点分别是点,,则,之间的距离可能是( )
A.0 B.5
C.6 D.7
5、襄阳市正在创建全国文明城市,某社区从今年6月1日起实施垃扱分类回收.下列图形分别是可回收物、厨余垃圾、有害垃圾及其它垃圾的标志,其中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
6、如图,在△ABC中,,点D是AB的中点,将△ACD沿CD对折得△A′CD.连接,连接AA′交CD于点E,若,,则CE的长为( )
A.4cm B.5cm C.6cm D.7cm
7、如图,在△ABC中,点A的坐标为(0,1),点B的坐标为(0,4),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是( )
A.(﹣4,3)
B.(﹣4,2)
C.(4,2)或(﹣4,3)
D.(4,2)或(﹣4,2)或(﹣4,3)
8、是点关于x轴的对称点.若一个正比例函数的图象经过点,则该函数的表达式为( )
A. B. C. D.
9、已知点经变换后到点B,下面的说法正确的是( )
A.点A与点B关于x轴对称,则点B的坐标为
B.点A绕原点按顺时针方向旋转90°后到点B,则点B的坐标为
C.点A与点B关于原点中心对称,则点B的坐标为
D.点A先向上平移3个单位,再向右平移4个单位到点B,则点B的坐标为
10、如图,将 ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A.66° B.104° C.114° D.124°
二、填空题(共 10 小题)
1、如图,在等边△ABC中,AD⊥BC,垂足为点D,AD=4,P是AD上一动点,E为AB的中点,连接PE,PB,则PB+PE的最小值为 ___.
2、在平面直角坐标系中,点A(2,m)在直线上,点A关于y轴对称的点B恰好落在直线上,则k的值为___.
3、如图,和关于直线AB对称,和关于直线AC对称,CD与AE交于点F,若,,则的度数为________.
4、在菱形ABCD中,∠B=60°,BC=2cm,M为AB的中点,N为BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE,CE,当△CDE为等腰三角形时,线段BN的长为_____.
5、如图,在中,将沿直线折叠,使点B落在点D的位置,若,,则的度数是__________.
6、如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,点P2020的坐标是__.
7、把一张边长为8cm的正方形纸片按如图所示的方法对折两次后剪去两个角,打开后得到一个正多边形.
(1)如果打开后得到一个正方形,则这个正方形的边长为______.
(2)有以下5个正多边形:①正五边形;②正六边形;③正八边形;④正十边形;⑤正十二边形,其中打开后可以得到是______.(只填序号)
8、如图,方格图中,将其中一个小方格的中心画上半径相等的圆,使整个图形为轴对称图形,这样的轴对称图形共有_________ 个.
9、已知点,若点M关于x轴的对称点在第三象限,则a的取值范围是______.
10、如图,在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,2),点A与点C(-3,2)之间的距离为 _____,点D在y轴上运动,当AD+BD的值最小时,点D的坐标为 _____,此时AD+BD的最小值为 _____.
三、解答题(共 6 小题)
1、如图所示,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1)B(4,2)C(2,3).
(1)在图中画出△ABC关于x轴对称的图形△A1B1C1;
(2)在图中,若B2(﹣4,2)与点B关于一条直线成轴对称,则这条对称轴是 ,此时C点关于这条直线的对称点C2的坐标为 ;
(3)△A1B1C1的面积为 ;
(4)在y轴上确定一点P,使△APB的周长最小.(注:不写作法,不求坐标,只保留作图痕迹)
2、如图,在平面直角坐标系中,已知
(1)在图中作出ABC关于轴的对称图形;
(2)若将ABC向右平移2个单位得到,则点B的对应点的坐标是______;
(3)求的长及ABC的面积.
3、如图,在正方形网格中,是格点三角形.
(1)画出,使得和关于直线对称;
(2)请在直线上找一点(即画出点),使点到点和点的距离之和最小;
(3)求的面积.
4、如图,三个顶点的坐标分别为
(1)若与关于y轴成轴对称,在图中画出,点坐标为__________;
(2)若直线与y轴相交于点,在y轴上是否存在点Q.使得,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3)在x轴上找一点P,使的值最小,点P的坐标是____________.
5、如图,长方形,点E是上的一点,将沿折叠后得到,且点O在长方形内部.已知,.
(1)如图1,若,求四边形的面积.
(2)如图2,延长交于F,连结,将沿折叠,当点D的对称点恰好为点O时,求四边形的面积.
(3)如图3,在(2)的条件下,延长交于点G,连结,将沿折叠,当点C的对称点恰好为点O时,求四边形的面积.
6、如图,三个顶点的坐标分别是,,.
(1)试画出关于轴对称的,并写出、、的坐标;
(2)在轴上求作一点,使周长最小,试画出,直接写出点的坐标.
