2022-2023学年人教版九年级数学下册27.2.3相似三角形应用举例课后强化练习(无答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册27.2.3相似三角形应用举例课后强化练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 444.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 21:16:05 | ||
图片预览


文档简介
27.2.3相似三角形应用举例课后强化
班级:________ 姓名:________
一、单选题(共 10 小题)
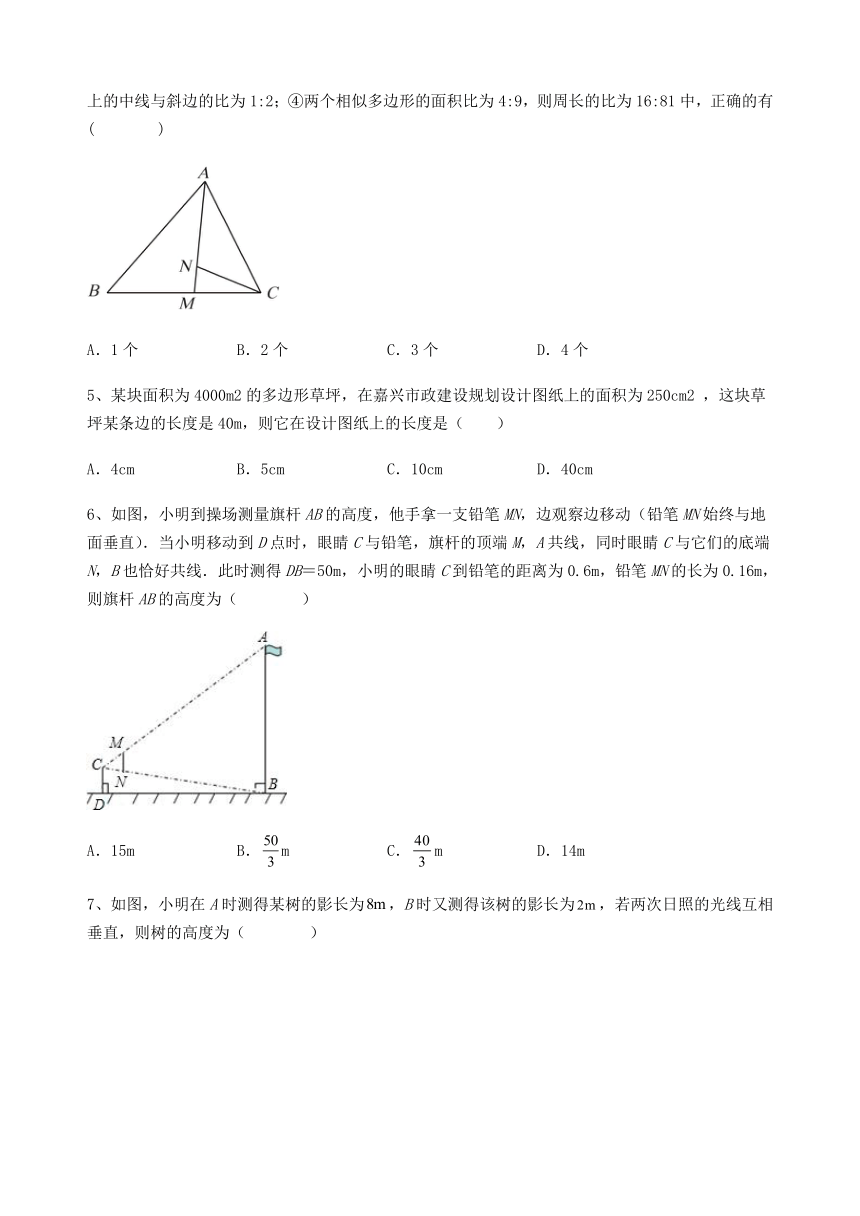
1、一人坐在理发椅上理发,眼睛与前面墙上宽0.6米的镜子相距1米,他从镜中恰好看到背后墙上宽2.4米的壁画,则此镜面与背后墙壁的距离是( )
A.2米 B.3米 C.4米 D.5米
2、图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,和相交于点O,点A,B之间的距离为1.2米,,根据图2中的数据可得点C,D之间的距离为( )
A.0.8米 B.0.86米 C.0.96米 D.1米
3、如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )
A.7.2 cm B.5.4 cm C.3.6 cm D.0.6 cm
4、下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )
A.1个 B.2个 C.3个 D.4个
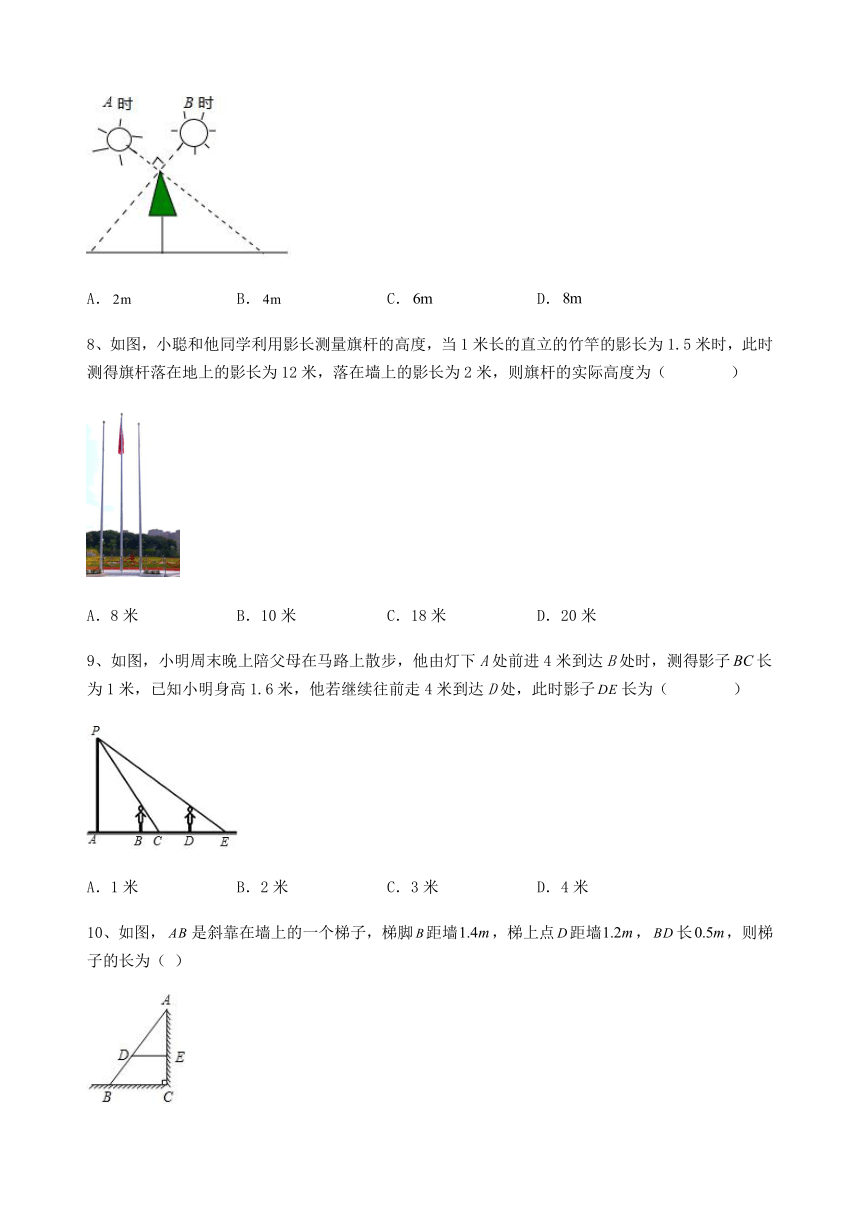
5、某块面积为4000m2的多边形草坪,在嘉兴市政建设规划设计图纸上的面积为250cm2 ,这块草坪某条边的长度是40m,则它在设计图纸上的长度是( )
A.4cm B.5cm C.10cm D.40cm
6、如图,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直).当小明移动到D点时,眼睛C与铅笔,旗杆的顶端M,A共线,同时眼睛C与它们的底端N,B也恰好共线.此时测得DB=50m,小明的眼睛C到铅笔的距离为0.6m,铅笔MN的长为0.16m,则旗杆AB的高度为( )
A.15m B.m C.m D.14m
7、如图,小明在A时测得某树的影长为,B时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为( )
A. B. C. D.
8、如图,小聪和他同学利用影长测量旗杆的高度,当1米长的直立的竹竿的影长为1.5米时,此时测得旗杆落在地上的影长为12米,落在墙上的影长为2米,则旗杆的实际高度为( )
A.8米 B.10米 C.18米 D.20米
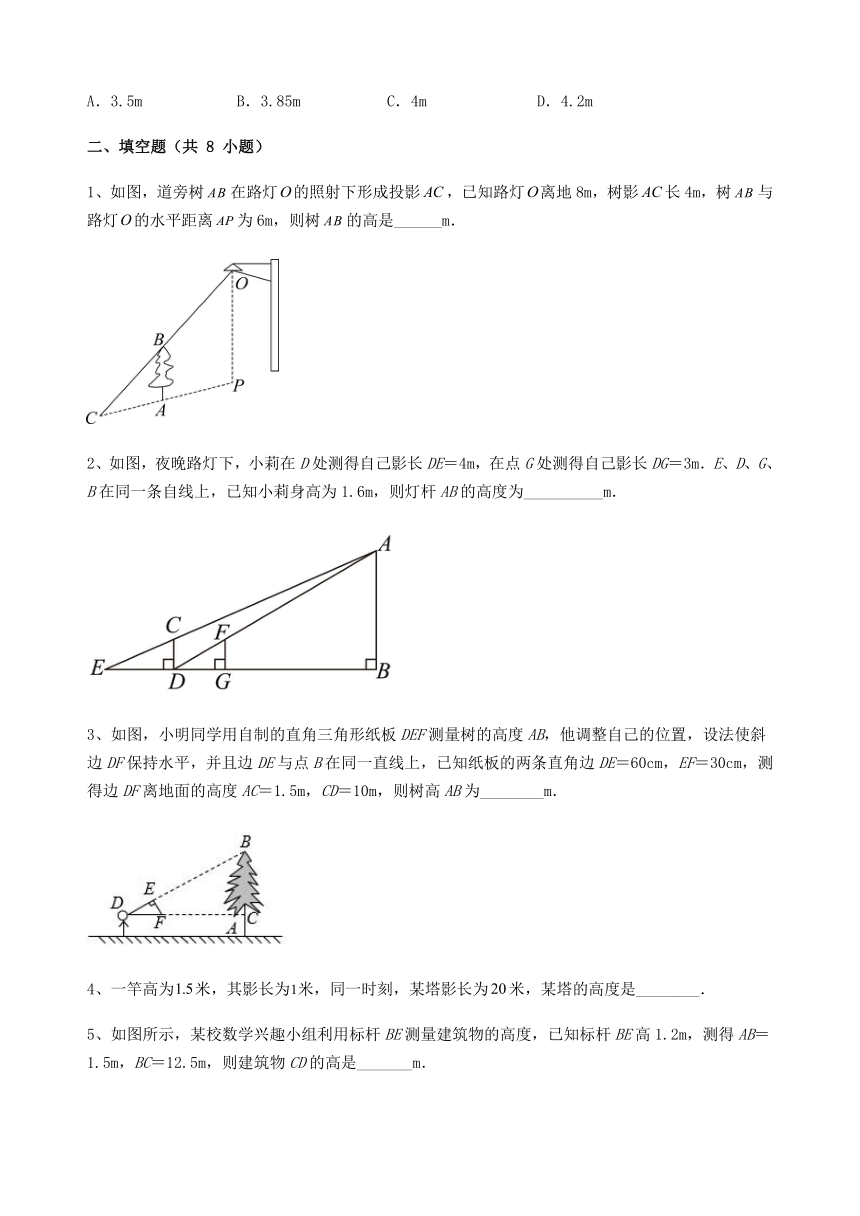
9、如图,小明周末晚上陪父母在马路上散步,他由灯下A处前进4米到达B处时,测得影子长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子长为( )
A.1米 B.2米 C.3米 D.4米
10、如图,是斜靠在墙上的一个梯子,梯脚距墙,梯上点距墙,长,则梯子的长为( )
A.3.5m B.3.85m C.4m D.4.2m
二、填空题(共 8 小题)
1、如图,道旁树在路灯的照射下形成投影,已知路灯离地8m,树影长4m,树与路灯的水平距离为6m,则树的高是______m.
2、如图,夜晚路灯下,小莉在D处测得自己影长DE=4m,在点G处测得自己影长DG=3m.E、D、G、B在同一条自线上,已知小莉身高为1.6m,则灯杆AB的高度为__________m.
3、如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=60cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,则树高AB为________m.
4、一竿高为米,其影长为米,同一时刻,某塔影长为米,某塔的高度是________.
5、如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.2m,测得AB=1.5m,BC=12.5m,则建筑物CD的高是_______m.
6、如图,是用卡钳测量容器内径的示意图.量得卡钳上A,D两端点的距离为4cm,,则容器的内径BC的长为_____cm.
7、贺哲同学的身高1.86米,影子长3米,同一时刻金老师的影子长2.7米,则金老师的身高为________米(结果保留两位小数)。
8、如图,为测量出湖边不可直接到达的A、B间的距离,测量人员选取一定点O,使A、O、C和B、O、D分别在同一直线上,测出CD=150米,且OB=3OD,OA=3OC,则AB=____米.
三、解答题(共 6 小题)
1、如图所示,小明站在B处想借助平面镜测量D处一棵大树的高度CD.他把平面镜平放在水平地面上,调整平面镜的位置到点P处,让自己通过平面镜刚好能看见大树的顶端C.
(1)若小明测得眼睛离地面的高度AB=1.6m,BP=2m,则他还需要测量哪条线段的长度即可求得大树的高度:(用字母a表示);
(2)在(1)的条件下,求树的高度CD.(用字母a的代数式表示)
2、如图,为了测量一旗杆的高度,小明立了两根高2m的标杆、(标杆与地面垂直且点B、C、D在一条线上),两标杆之间的距离,从C处沿方向退后1.5m到点G,眼睛贴着地面观察A点,G,E,A三点成一线;从D处沿方向退后3m到点H,眼睛贴着地面观察A点,H,F,A三点成一线.求旗杆的高度.
3、如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
4、材料阅读:
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点(无需写解答过程);
(3)如图③所示的矩形ABCD,将矩形ABCD沿CM折叠后,点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究点E的位置.
5、如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面,坡角.在阳光下,小明观察到在地面上的影长为,在坡面上的影长为.同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.
6、小红和小亮经常去学校图书馆里阅读各种书籍,两位同学想利用刚学过的测量知识来测量该图书馆的高度.某天,他们带着测量工具来图书馆前,但由于校园整体规划的原因,他们无法到达图书馆底部.于是小亮在地面上的点处放置了一个平面镜,小红从处出发沿着方向移动,当移动到点处时,刚好在平面镜内看到图书馆的顶端的像,此时,测得米,小红眼睛到地面的距离为1.6米;然后,小亮沿方向移动到点,用测量器测得图书馆顶端的仰角为45°,此时,测得,测量器的高度米.已知点、、、在同一水平直线上,且、、均垂直于,求该图书馆的高度.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、一人坐在理发椅上理发,眼睛与前面墙上宽0.6米的镜子相距1米,他从镜中恰好看到背后墙上宽2.4米的壁画,则此镜面与背后墙壁的距离是( )
A.2米 B.3米 C.4米 D.5米
2、图1是伸缩折叠不锈钢晾衣架的实物图,图2是它的侧面示意图,和相交于点O,点A,B之间的距离为1.2米,,根据图2中的数据可得点C,D之间的距离为( )
A.0.8米 B.0.86米 C.0.96米 D.1米
3、如图,比例规是一种画图工具,它由长度相等的两脚AC和BD交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度3的地方(即同时使OA=3OC,OB=3OD),然后张开两脚,使A,B两个尖端分别在线段a的两个端点上,当CD=1.8cm时,则AB的长为( )
A.7.2 cm B.5.4 cm C.3.6 cm D.0.6 cm
4、下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( )
A.1个 B.2个 C.3个 D.4个
5、某块面积为4000m2的多边形草坪,在嘉兴市政建设规划设计图纸上的面积为250cm2 ,这块草坪某条边的长度是40m,则它在设计图纸上的长度是( )
A.4cm B.5cm C.10cm D.40cm
6、如图,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直).当小明移动到D点时,眼睛C与铅笔,旗杆的顶端M,A共线,同时眼睛C与它们的底端N,B也恰好共线.此时测得DB=50m,小明的眼睛C到铅笔的距离为0.6m,铅笔MN的长为0.16m,则旗杆AB的高度为( )
A.15m B.m C.m D.14m
7、如图,小明在A时测得某树的影长为,B时又测得该树的影长为,若两次日照的光线互相垂直,则树的高度为( )
A. B. C. D.
8、如图,小聪和他同学利用影长测量旗杆的高度,当1米长的直立的竹竿的影长为1.5米时,此时测得旗杆落在地上的影长为12米,落在墙上的影长为2米,则旗杆的实际高度为( )
A.8米 B.10米 C.18米 D.20米
9、如图,小明周末晚上陪父母在马路上散步,他由灯下A处前进4米到达B处时,测得影子长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子长为( )
A.1米 B.2米 C.3米 D.4米
10、如图,是斜靠在墙上的一个梯子,梯脚距墙,梯上点距墙,长,则梯子的长为( )
A.3.5m B.3.85m C.4m D.4.2m
二、填空题(共 8 小题)
1、如图,道旁树在路灯的照射下形成投影,已知路灯离地8m,树影长4m,树与路灯的水平距离为6m,则树的高是______m.
2、如图,夜晚路灯下,小莉在D处测得自己影长DE=4m,在点G处测得自己影长DG=3m.E、D、G、B在同一条自线上,已知小莉身高为1.6m,则灯杆AB的高度为__________m.
3、如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=60cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,则树高AB为________m.
4、一竿高为米,其影长为米,同一时刻,某塔影长为米,某塔的高度是________.
5、如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.2m,测得AB=1.5m,BC=12.5m,则建筑物CD的高是_______m.
6、如图,是用卡钳测量容器内径的示意图.量得卡钳上A,D两端点的距离为4cm,,则容器的内径BC的长为_____cm.
7、贺哲同学的身高1.86米,影子长3米,同一时刻金老师的影子长2.7米,则金老师的身高为________米(结果保留两位小数)。
8、如图,为测量出湖边不可直接到达的A、B间的距离,测量人员选取一定点O,使A、O、C和B、O、D分别在同一直线上,测出CD=150米,且OB=3OD,OA=3OC,则AB=____米.
三、解答题(共 6 小题)
1、如图所示,小明站在B处想借助平面镜测量D处一棵大树的高度CD.他把平面镜平放在水平地面上,调整平面镜的位置到点P处,让自己通过平面镜刚好能看见大树的顶端C.
(1)若小明测得眼睛离地面的高度AB=1.6m,BP=2m,则他还需要测量哪条线段的长度即可求得大树的高度:(用字母a表示);
(2)在(1)的条件下,求树的高度CD.(用字母a的代数式表示)
2、如图,为了测量一旗杆的高度,小明立了两根高2m的标杆、(标杆与地面垂直且点B、C、D在一条线上),两标杆之间的距离,从C处沿方向退后1.5m到点G,眼睛贴着地面观察A点,G,E,A三点成一线;从D处沿方向退后3m到点H,眼睛贴着地面观察A点,H,F,A三点成一线.求旗杆的高度.
3、如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
4、材料阅读:
如图①,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图②,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点(无需写解答过程);
(3)如图③所示的矩形ABCD,将矩形ABCD沿CM折叠后,点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究点E的位置.
5、如图,公园内有一个垂直于地面的立柱AB,其旁边有一个坡面,坡角.在阳光下,小明观察到在地面上的影长为,在坡面上的影长为.同一时刻,小明测得直立于地面长60cm的木杆的影长为90cm(其影子完全落在地面上).求立柱AB的高度.
6、小红和小亮经常去学校图书馆里阅读各种书籍,两位同学想利用刚学过的测量知识来测量该图书馆的高度.某天,他们带着测量工具来图书馆前,但由于校园整体规划的原因,他们无法到达图书馆底部.于是小亮在地面上的点处放置了一个平面镜,小红从处出发沿着方向移动,当移动到点处时,刚好在平面镜内看到图书馆的顶端的像,此时,测得米,小红眼睛到地面的距离为1.6米;然后,小亮沿方向移动到点,用测量器测得图书馆顶端的仰角为45°,此时,测得,测量器的高度米.已知点、、、在同一水平直线上,且、、均垂直于,求该图书馆的高度.
