2022-2023学年京改版八年级数学下册第十四章14.4 一次函数同步精练(无答案)
文档属性
| 名称 | 2022-2023学年京改版八年级数学下册第十四章14.4 一次函数同步精练(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 360.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 22:00:30 | ||
图片预览


文档简介
第十四章 一次函数 二 一次函数同步精练
班级:________ 姓名:________
一、单选题(共 10 小题)
1、一次函数的值随的增大而增大,则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
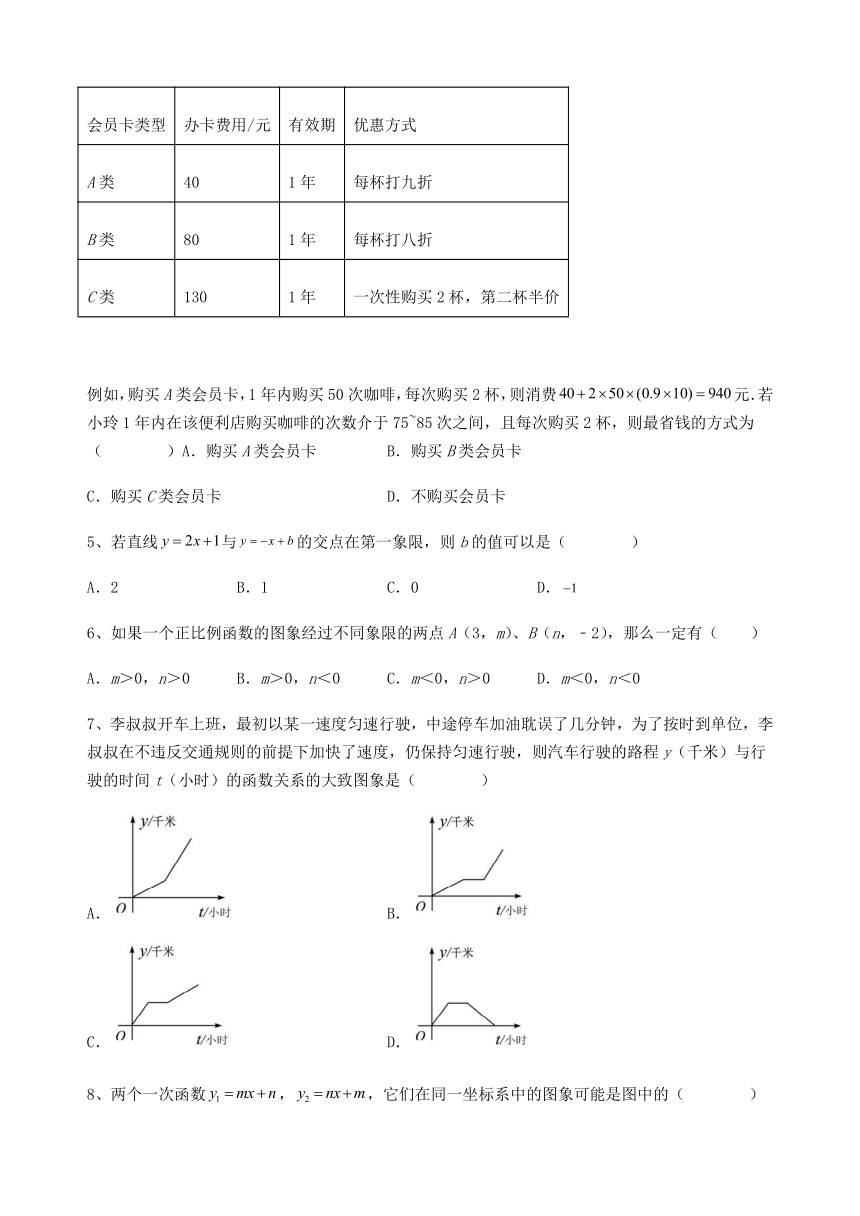
2、已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A.15km B.16km C.44km D.45km
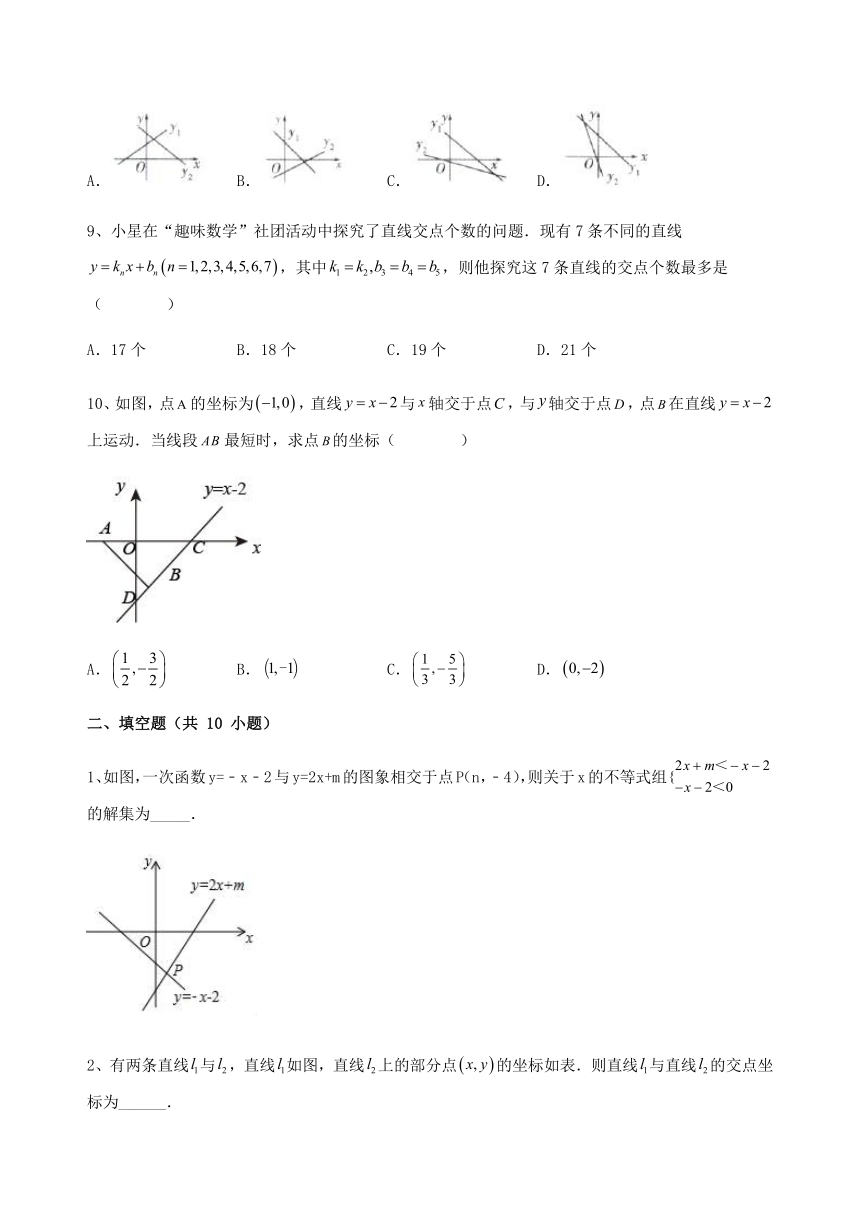
3、如图所示,直线分别与x轴、y轴交于点A、B,以线段为边,在第二象限内作等腰直角,,则过B、C两点直线的解析式为( )
A. B. C. D.
4、某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
会员卡类型 办卡费用/元 有效期 优惠方式
A类 40 1年 每杯打九折
B类 80 1年 每杯打八折
C类 130 1年 一次性购买2杯,第二杯半价
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )A.购买A类会员卡 B.购买B类会员卡
C.购买C类会员卡 D.不购买会员卡
5、若直线与的交点在第一象限,则b的值可以是( )
A.2 B.1 C.0 D.
6、如果一个正比例函数的图象经过不同象限的两点A(3,m)、B(n,﹣2),那么一定有( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
7、李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )
A. B.
C. D.
8、两个一次函数,,它们在同一坐标系中的图象可能是图中的( )
A. B. C. D.
9、小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线,其中,则他探究这7条直线的交点个数最多是( )
A.17个 B.18个 C.19个 D.21个
10、如图,点的坐标为,直线与轴交于点,与轴交于点,点在直线上运动.当线段最短时,求点的坐标( )
A. B. C. D.
二、填空题(共 10 小题)
1、如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组的解集为_____.
2、有两条直线与,直线如图,直线上的部分点的坐标如表.则直线与直线的交点坐标为______.
… 0 1 2 …
… 0 1 …
3、若整数使关于的一次函数不经过第三象限,且使关于的不等式组有且仅有4个整数解,则所有满足条件的整数的值之和为______.
4、甲乙两地相距450千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,折线OAB表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,线段CD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,C(1,0),则在轿车追上货车后至到达乙地前,当轿车在货车前105千米时,所用的时间x为______小时.
5、将直线向右平移2个单位长度后,所得直线的解析式是__________.
6、如图,在平面直角坐标系中,已知,在x轴上取两点C,D(点C在点D左侧),且始终保持,线段在x轴上平移,当的值最小时,点C的坐标为________.
7、某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 大巴车(最多可坐55人) 中巴车(最多可坐39人) 小巴车(最多可坐26人)
每车租金(元∕天) 900 800 550
则租车一天的最低费用为____元.
8、在平面直角坐标系中,O为原点,直线y=kx+b交x轴于A(-3,0),交y轴于B,且三角形AOB的面积为6,则k=________.
9、将直线先向右平移1个单位,再向上平移2个单位得到的直线解析式是______.
10、已知一次函数的图象不过第二象限.
(1)k的取值范围为______.
(2)对于一次函数,若对任意实数x,,都成立,求k的取值范围为______.
三、解答题(共 6 小题)
1、如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于A、B两点,.
(1)求k的值;
(2)点P在线段AB上,连接OP.若,求点P的坐标;
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,求直线AC的表达式.
2、如图,已知,在直角坐标系中,直线y= x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向左移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发.
(1)求点A、C的坐标;
(2)若点B在y轴上,且与点A、C构成以AC为腰的等腰三角形,请直接写出所有符合条件的B点坐标.
(3)经过几秒钟,能使△POQ的面积为8个平方单位.
3、如图,在平面直角坐标系xOy中,直线y=x+4与x轴、y轴分别交于点A、点B,点D(0,﹣6)在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处,直线CD交AB于点E.
(1)求点A、B、C的坐标;
(2)求△ADE的面积;
(3)y轴上是否存在一点P,使得=,若存在,请直接写出点P的坐标;若不存在,请说明理由.
4、如图1,在平面直角坐标中,直线:与抽交于点,直线:与轴交于点,与相交于点.
(1)请直接写出点,点,点的坐标:_________,________,_______.
(2)如图2,动直线分别与直线、交于、两点.
①若,求的值;
②若存在,求出此时点的坐标;若不存在,请说明理由.
5、为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:
进价(元/斤) 售价(元/斤)
鲢鱼 5
草鱼 销量不超过200斤的部分 销量超过200斤的部分
8 7
已知老李购进10斤鲢鱼和20斤草鱼需要155元,购进20斤鲢鱼和10斤草鱼需要130元.
(1)求,的值;
(2)老李每天购进两种鱼共300斤,并在当天都销售完,其中销售鲢鱼不少于80斤且不超过120斤,设每天销售鲢鱼斤(销售过程中损耗不计).
①分别求出每天销售鲢鱼获利(元),销售草鱼获利(元)与的函数关系式,并写出的取值范围;
②端午节这天,老李让利销售,将鲢鱼售价每斤降低元,草鱼售价全部定为7元斤,为了保证当天销售这两种鱼总获利(元)的最小值不少于320元,求的最大值.
6、如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MNx轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、一次函数的值随的增大而增大,则点所在象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2、已知A,B两地相距60km,甲、乙两人沿同一条公路从A地出发到B地,甲骑自行车匀速行驶3h到达,乙骑摩托车.比甲迟1h出发,行至30km处追上甲,停留半小时后继续以原速行驶.他们离开A地的路程y与甲行驶时间x的函数图象如图所示.当乙再次追上甲时距离B地( )
A.15km B.16km C.44km D.45km
3、如图所示,直线分别与x轴、y轴交于点A、B,以线段为边,在第二象限内作等腰直角,,则过B、C两点直线的解析式为( )
A. B. C. D.
4、某便利店的咖啡单价为10元/杯,为了吸引顾客,该店共推出了三种会员卡,如下表:
会员卡类型 办卡费用/元 有效期 优惠方式
A类 40 1年 每杯打九折
B类 80 1年 每杯打八折
C类 130 1年 一次性购买2杯,第二杯半价
例如,购买A类会员卡,1年内购买50次咖啡,每次购买2杯,则消费元.若小玲1年内在该便利店购买咖啡的次数介于75~85次之间,且每次购买2杯,则最省钱的方式为( )A.购买A类会员卡 B.购买B类会员卡
C.购买C类会员卡 D.不购买会员卡
5、若直线与的交点在第一象限,则b的值可以是( )
A.2 B.1 C.0 D.
6、如果一个正比例函数的图象经过不同象限的两点A(3,m)、B(n,﹣2),那么一定有( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
7、李叔叔开车上班,最初以某一速度匀速行驶,中途停车加油耽误了几分钟,为了按时到单位,李叔叔在不违反交通规则的前提下加快了速度,仍保持匀速行驶,则汽车行驶的路程y(千米)与行驶的时间t(小时)的函数关系的大致图象是( )
A. B.
C. D.
8、两个一次函数,,它们在同一坐标系中的图象可能是图中的( )
A. B. C. D.
9、小星在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线,其中,则他探究这7条直线的交点个数最多是( )
A.17个 B.18个 C.19个 D.21个
10、如图,点的坐标为,直线与轴交于点,与轴交于点,点在直线上运动.当线段最短时,求点的坐标( )
A. B. C. D.
二、填空题(共 10 小题)
1、如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组的解集为_____.
2、有两条直线与,直线如图,直线上的部分点的坐标如表.则直线与直线的交点坐标为______.
… 0 1 2 …
… 0 1 …
3、若整数使关于的一次函数不经过第三象限,且使关于的不等式组有且仅有4个整数解,则所有满足条件的整数的值之和为______.
4、甲乙两地相距450千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,折线OAB表示货车离甲地的路程y(千米)与所用时间x(小时)之间的函数关系,线段CD表示轿车离甲地的路程y(千米)与x(小时)之间的函数关系,C(1,0),则在轿车追上货车后至到达乙地前,当轿车在货车前105千米时,所用的时间x为______小时.
5、将直线向右平移2个单位长度后,所得直线的解析式是__________.
6、如图,在平面直角坐标系中,已知,在x轴上取两点C,D(点C在点D左侧),且始终保持,线段在x轴上平移,当的值最小时,点C的坐标为________.
7、某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 大巴车(最多可坐55人) 中巴车(最多可坐39人) 小巴车(最多可坐26人)
每车租金(元∕天) 900 800 550
则租车一天的最低费用为____元.
8、在平面直角坐标系中,O为原点,直线y=kx+b交x轴于A(-3,0),交y轴于B,且三角形AOB的面积为6,则k=________.
9、将直线先向右平移1个单位,再向上平移2个单位得到的直线解析式是______.
10、已知一次函数的图象不过第二象限.
(1)k的取值范围为______.
(2)对于一次函数,若对任意实数x,,都成立,求k的取值范围为______.
三、解答题(共 6 小题)
1、如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于A、B两点,.
(1)求k的值;
(2)点P在线段AB上,连接OP.若,求点P的坐标;
(3)将直线AB绕点A逆时针旋转45°后得到直线AC,求直线AC的表达式.
2、如图,已知,在直角坐标系中,直线y= x+8与x轴、y轴分别交于点A、C,点P从A点开始以1个单位/秒的速度沿x轴向左移动,点Q从O点开始以2个单位/秒的速度沿y轴向上移动,如果P、Q两点同时出发.
(1)求点A、C的坐标;
(2)若点B在y轴上,且与点A、C构成以AC为腰的等腰三角形,请直接写出所有符合条件的B点坐标.
(3)经过几秒钟,能使△POQ的面积为8个平方单位.
3、如图,在平面直角坐标系xOy中,直线y=x+4与x轴、y轴分别交于点A、点B,点D(0,﹣6)在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处,直线CD交AB于点E.
(1)求点A、B、C的坐标;
(2)求△ADE的面积;
(3)y轴上是否存在一点P,使得=,若存在,请直接写出点P的坐标;若不存在,请说明理由.
4、如图1,在平面直角坐标中,直线:与抽交于点,直线:与轴交于点,与相交于点.
(1)请直接写出点,点,点的坐标:_________,________,_______.
(2)如图2,动直线分别与直线、交于、两点.
①若,求的值;
②若存在,求出此时点的坐标;若不存在,请说明理由.
5、为了切实保护汉江生态环境,襄阳市政府对汉江襄阳段实施全面禁渔.禁渔后,某水库自然生态养殖的鱼在市场上热销,经销商老李每天从该水库购进草鱼和鲢鱼进行销售,两种鱼的进价和售价如下表所示:
进价(元/斤) 售价(元/斤)
鲢鱼 5
草鱼 销量不超过200斤的部分 销量超过200斤的部分
8 7
已知老李购进10斤鲢鱼和20斤草鱼需要155元,购进20斤鲢鱼和10斤草鱼需要130元.
(1)求,的值;
(2)老李每天购进两种鱼共300斤,并在当天都销售完,其中销售鲢鱼不少于80斤且不超过120斤,设每天销售鲢鱼斤(销售过程中损耗不计).
①分别求出每天销售鲢鱼获利(元),销售草鱼获利(元)与的函数关系式,并写出的取值范围;
②端午节这天,老李让利销售,将鲢鱼售价每斤降低元,草鱼售价全部定为7元斤,为了保证当天销售这两种鱼总获利(元)的最小值不少于320元,求的最大值.
6、如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MNx轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
同课章节目录
