2022-2023学年北师大数学八年级上册第一章 勾股定理 单元过关测试卷(无答案)
文档属性
| 名称 | 2022-2023学年北师大数学八年级上册第一章 勾股定理 单元过关测试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 185.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 15:36:15 | ||
图片预览

文档简介
第一章 勾股定理 单元过关测试卷
一、选择题
如图,字母 所代表的正方形的面积是
A. B. C. D.
下列各组数中,以 ,, 为边的三角形不是直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
将一根 的筷子,置于底面直径为 ,高 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 ,则 的取值范围是
A. B.
C. D.
图 是第七届国际数学教育大会()的会徽图案,它是由一串有公共顶点 的直角三角形(如图 所示)演化而成的.如果图 中的 ,那么 的长为
A. B. C. D.
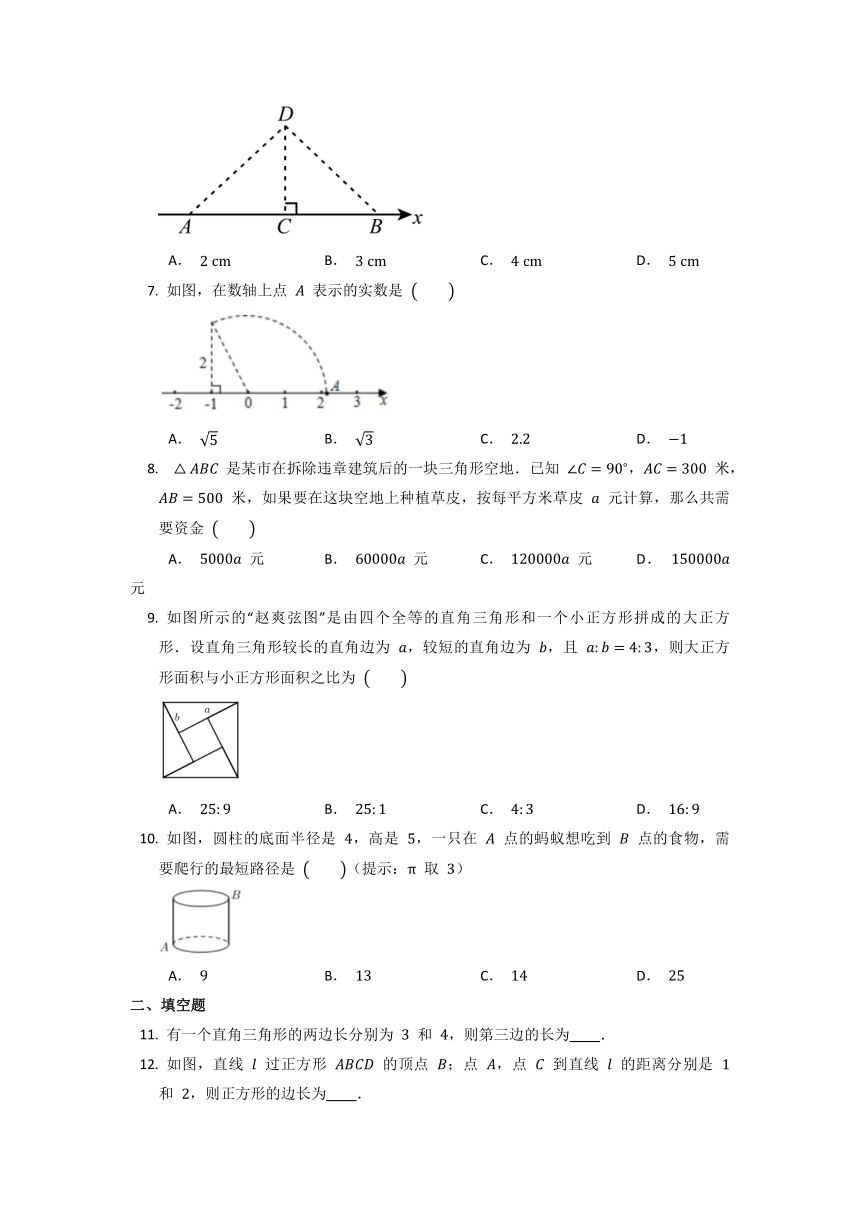
如图,在一块平地上,张大爷家屋前 米远处有一棵大树,在一次强风中,这棵大树从离地面 米处折断倒下,量得倒下部分的长是 米,大树倒下时能砸到张大爷的房子吗
A.一定不会 B.可能会
C.一定会 D.以上答案都不对
如图,长为 的橡皮筋放置在 轴上,固定两端 和 ,然后把中点 向上拉升 至 点,则橡皮筋被拉长了
A. B. C. D.
如图,在数轴上点 表示的实数是
A. B. C. D.
是某市在拆除违章建筑后的一块三角形空地.已知 , 米, 米,如果要在这块空地上种植草皮,按每平方米草皮 元计算,那么共需要资金
A. 元 B. 元 C. 元 D. 元
如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的大正方形.设直角三角形较长的直角边为 ,较短的直角边为 ,且 ,则大正方形面积与小正方形面积之比为
A. B. C. D.
如图,圆柱的底面半径是 ,高是 ,一只在 点的蚂蚁想吃到 点的食物,需要爬行的最短路径是 (提示: 取 )
A. B. C. D.
二、填空题
有一个直角三角形的两边长分别为 和 ,则第三边的长为 .
如图,直线 过正方形 的顶点 ;点 ,点 到直线 的距离分别是 和 ,则正方形的边长为 .
如图,在 中,,,,按图中所示方法将 沿 折叠,使点 落在 边的 处,那么 .
如图,某港口 位于南北延伸的海岸线上,东面是大海,“远洋”号、“长峰”号两艘轮船同时离开港口 ,各自沿固定方向航行,“远洋”号每小时航行 ,“长峰”号每小时航行 ,它们离开港口 小时后,分别到达 , 两个位置,且 ,已知“远洋”号沿着北偏东 方向航行,那么“长峰”号航行的方向是 .
如图, 中,,,, 与 的角平分线相交于点 ,过点 作 ,垂足为点 ,则线段 的长为 .
如图是一个三级台阶,它的每一级的长、宽、高分别为 ,,. 和 是这个台阶上两个相对的端点,点 处有一只蚂蚁,想到点 处去吃可口的食物,则蚂蚁沿着台阶爬行到点 的最短路程为 .
三、解答题
如图, 中,,, 是 边上的垂直平分线, 的周长为 ,求 的长.
如图,已知四边形 中,,,,,,则四边 的面积是多少?
已知 ,, 满足 .
(1) 求 ,, 的值.
(2) 以 ,, 为三边能否构成直角三角形?如果构成三角形,那么哪个角是直角,请说明理由.
如图,一根直立于水中的芦苇 比水面 高出 ,即 ,一阵风吹来,芦苇的顶端 恰好到达水面 的 处,且 到 的距离 ,已知 ,求水的深度 与这根芦苇的长度 分别是多少 ?
如图,每个小正方形的边长都是 .
(1) 请在图 中画出一个面积为 的正方形.
(2) 如图 际示,点 ,, 均为格点,通过计算求出点 到 所在直线的距离.
如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点 在 的延长线上,设想过 点作直线 的垂线 ,过点 作一直线(在山的旁边经过),与 相交于 点,经测量 , 米,求直线 上距离 点多远的 处开挖?(,精确到 米)
一、选择题
如图,字母 所代表的正方形的面积是
A. B. C. D.
下列各组数中,以 ,, 为边的三角形不是直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
将一根 的筷子,置于底面直径为 ,高 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为 ,则 的取值范围是
A. B.
C. D.
图 是第七届国际数学教育大会()的会徽图案,它是由一串有公共顶点 的直角三角形(如图 所示)演化而成的.如果图 中的 ,那么 的长为
A. B. C. D.
如图,在一块平地上,张大爷家屋前 米远处有一棵大树,在一次强风中,这棵大树从离地面 米处折断倒下,量得倒下部分的长是 米,大树倒下时能砸到张大爷的房子吗
A.一定不会 B.可能会
C.一定会 D.以上答案都不对
如图,长为 的橡皮筋放置在 轴上,固定两端 和 ,然后把中点 向上拉升 至 点,则橡皮筋被拉长了
A. B. C. D.
如图,在数轴上点 表示的实数是
A. B. C. D.
是某市在拆除违章建筑后的一块三角形空地.已知 , 米, 米,如果要在这块空地上种植草皮,按每平方米草皮 元计算,那么共需要资金
A. 元 B. 元 C. 元 D. 元
如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的大正方形.设直角三角形较长的直角边为 ,较短的直角边为 ,且 ,则大正方形面积与小正方形面积之比为
A. B. C. D.
如图,圆柱的底面半径是 ,高是 ,一只在 点的蚂蚁想吃到 点的食物,需要爬行的最短路径是 (提示: 取 )
A. B. C. D.
二、填空题
有一个直角三角形的两边长分别为 和 ,则第三边的长为 .
如图,直线 过正方形 的顶点 ;点 ,点 到直线 的距离分别是 和 ,则正方形的边长为 .
如图,在 中,,,,按图中所示方法将 沿 折叠,使点 落在 边的 处,那么 .
如图,某港口 位于南北延伸的海岸线上,东面是大海,“远洋”号、“长峰”号两艘轮船同时离开港口 ,各自沿固定方向航行,“远洋”号每小时航行 ,“长峰”号每小时航行 ,它们离开港口 小时后,分别到达 , 两个位置,且 ,已知“远洋”号沿着北偏东 方向航行,那么“长峰”号航行的方向是 .
如图, 中,,,, 与 的角平分线相交于点 ,过点 作 ,垂足为点 ,则线段 的长为 .
如图是一个三级台阶,它的每一级的长、宽、高分别为 ,,. 和 是这个台阶上两个相对的端点,点 处有一只蚂蚁,想到点 处去吃可口的食物,则蚂蚁沿着台阶爬行到点 的最短路程为 .
三、解答题
如图, 中,,, 是 边上的垂直平分线, 的周长为 ,求 的长.
如图,已知四边形 中,,,,,,则四边 的面积是多少?
已知 ,, 满足 .
(1) 求 ,, 的值.
(2) 以 ,, 为三边能否构成直角三角形?如果构成三角形,那么哪个角是直角,请说明理由.
如图,一根直立于水中的芦苇 比水面 高出 ,即 ,一阵风吹来,芦苇的顶端 恰好到达水面 的 处,且 到 的距离 ,已知 ,求水的深度 与这根芦苇的长度 分别是多少 ?
如图,每个小正方形的边长都是 .
(1) 请在图 中画出一个面积为 的正方形.
(2) 如图 际示,点 ,, 均为格点,通过计算求出点 到 所在直线的距离.
如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点 在 的延长线上,设想过 点作直线 的垂线 ,过点 作一直线(在山的旁边经过),与 相交于 点,经测量 , 米,求直线 上距离 点多远的 处开挖?(,精确到 米)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
