2022-2023学年华东师大版七年级数学下册7.4实践与探索 课后练习(无答案)
文档属性
| 名称 | 2022-2023学年华东师大版七年级数学下册7.4实践与探索 课后练习(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 330.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-31 00:00:00 | ||
图片预览

文档简介
《7.4实践与探索》课后练习
班级:________ 姓名:________
一、单选题(共 10 小题)
1、《九章算术》有个题目,大意是:“五只雀、六只燕,共重16两,雀重燕轻,互换其中一只,恰好一样重.”设每只雀、燕的重量分别为x两,y两,可得方程组是( )
A. B.
C. D.
2、请阅读下面的诗句:“栖树一群鸦,鸦树不知数.三只栖一树,五只没处去.五只栖一树,闲了一棵树.请你仔细数,鸦树各几何?”若设鸦有只,树有棵,则可列方程组为( )
A. B.
C. D.
3、“某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的 A、B 两种长方体形状的无盖纸盒.现 有正方形纸板 120 张,长方形纸板 360 张,刚好全部用完,问能做成多少个 A 型盒子?”则下列结论 正确的个数是( )
①甲同学:设 A 型盒子个数为 x 个,根据题意可得: 4x 3 360
②乙同学:设 B 型盒中正方形纸板的个数为 m 个,根据题意可得: 3 4(120 m) 360
③A 型盒 72 个
④B 型盒中正方形纸板 48 个
A.1 B.2 C.3 D.4
4、在“幻方拓展课程”探索中,小明在如图的3×3方格内填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则x﹣y=( )
A.2 B.4 C.6 D.8
5、我国古代数学名著《算法统宗》中记载:“今有绫七尺, 罗九尺,共价适等; 只云罗每尺价比绫每尺少钱三十六文,问各钱价若干 ” 意思是: 现在有一匹7尺长的绫布和一匹9 尺长的罗布恰好一样贵,只知道每尺罗布比绫布便宜36文,问两种布每尺各多少钱 设绫布每尺文,罗布每尺文,那么可列方程组为( )
A. B. C. D.
6、古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思就是说,有一群乌鸦要到树林休息,如果每棵树上落坐有三只乌鸦,则有五个落在地上;如果每棵树上落坐有五只乌鸦,则有一棵树没有乌鸦落坐,请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组( )
A. B. C. D.
7、某公司用3000元购进两种货物,货物卖出后,一种货物的利润率是10%,另一种货物的利润率是11%,两种货物共获利315元,如果设该公司购进这两和货物所用的费用分别为x元,y元,则列出的方程组是( )
A. B.
C. D.
8、在某场CBA比赛中,某位运动员的技术统计如下表所示:
技术 上场时间(分钟) 出手投篮(次) 投中(次) 罚球得分(分) 篮板(个) 防攻(次) 个人总得分(分)
数据 38 27 11 6 3 4 33
注:①表中出手投篮次数和投中次数均不包括罚球;
②总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,本场比赛中该运动员投中两分球和三分球各( )个.
A.5,6 B.6,5 C.4,7 D.7,4
9、某校组织一批学生去研学,若单独租用45座新能源客车若干辆,则有15人没有座位;若单独租用35座新能源客车,则用车数量将增加2辆,并空出15个座位.现在要求同时租用 45座和35座两种车型的新能源客车,既保证每人有座位,又保证每辆车不空座位,则需45座和35座两种车型的数量分别为( )
A.3辆、2辆 B.2辆、3辆 C.1辆、4辆 D.4辆、1辆
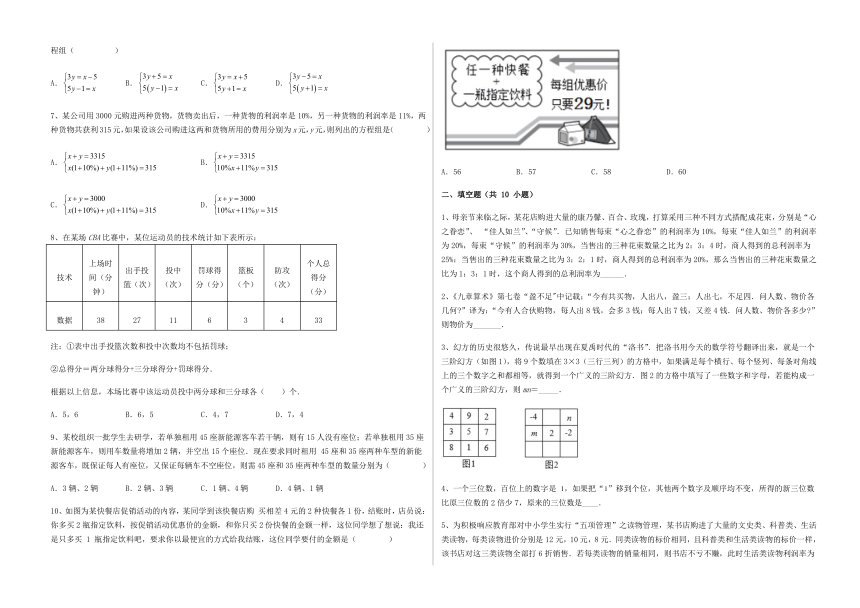
10、如图为某快餐店促销活动的内容,某同学到该快餐店购 买相差4元的2种快餐各1份,结账时,店员说:你多买2瓶指定饮料,按促销活动优惠价的金额,和你只买2份快餐的金额一样,这位同学想了想说:我还是只多买 1 瓶指定饮料吧,要求你以最便宜的方式给我结账,这位同学要付的金额是( )
A.56 B.57 C.58 D.60
二、填空题(共 10 小题)
1、母亲节来临之际,某花店购进大量的康乃馨、百合、玫瑰,打算采用三种不同方式搭配成花束,分别是“心之眷恋”、 “佳人如兰”、“守候”.已知销售每束“心之眷恋”的利润率为10%,每束“佳人如兰”的利润率为20%,每束“守候”的利润率为30%,当售出的三种花束数量之比为2:3:4时,商人得到的总利润率为25%:当售出的三种花束数量之比为3:2:1时,商人得到的总利润率为20%,那么当售出的三种花束数量之比为1:3:1时,这个商人得到的总利润率为______.
2、《九章算术》第七卷“盈不足"中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何 ”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少 ”则物价为_______.
3、幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn=_____.
4、一个三位数,百位上的数字是 ,如果把“”移到个位,其他两个数字及顺序均不变,所得的新三位数比原三位数的2倍少7,原来的三位数是____.
5、为积极响应教育部对中小学生实行“五项管理”之读物管理,某书店购进了大量的文史类、科普类、生活类读物,每类读物进价分别是12元,10元,8元.同类读物的标价相同,且科普类和生活类读物的标价一样,该书店对这三类读物全部打6折销售.若每类读物的销量相同,则书店不亏不赚,此时生活类读物利润率为.若文史类、科普类、生活类销量之比是,则书店销售这三类读物的总利润率为_____.(利润率)
6、某体育场的环形跑道长400m,甲 乙分别以一定的速度练习长跑和自行车,如果反向而行,他们每隔30s相遇一次.如果同向而行,那么每隔80s乙就追上甲一次.则甲的速度是________m/s.
7、《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来就是 类似地,图2所示的算筹图我们可以用方程组形式表述为__________.
8、学校计划购买和两种品牌的足球,已知一个品牌足球60元,一个品牌足球75元.学校准备将1500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有_________种.
9、为了开展“阳光体育”活动,某班计划购买甲、乙两种体育用品每种体育用品都购买,其中甲种体育用品每件20元,乙种体育用品每件30元,共用去150元,请你设计一下,共有______种购买方案.
10、某商场购进商品后,加价40%作为销售价.五一期间,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款448元.两种商品原销售价之和为560元.则两种商品进价分别为________元.
三、解答题(共 6 小题)
1、某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.若购买这两类球的总金额为4600元,则篮球、足球各买了多少个?
2、目前,新型冠状病毒在我国虽可控可防,但不可松懈某校欲购置规格分别为和的甲、乙两种免洗手消毒液若干瓶,已知购买1瓶甲和1瓶乙免洗手消毒液需要32元,购5瓶甲和3瓶乙免洗手消毒液需要120元.
(1)求甲、乙两种免洗手消毒液的单价.
(2)该校在校师生共1000人,平均每人每天都需使用的免洗手消毒液,若校方采购甲、乙两免洗手消毒液共花费4000元,则这批消毒液可使用多少天?
(3)为节约成本,该校购买散装免洗手消毒液进行分装,现需将的免洗手消毒液全部装入最大容量分别为和的两种空瓶中(每瓶均装满),若分装时平均每瓶需损耗,请问如何分装能使总损耗最小,求出此时需要的两种空瓶的数量.
3、若m是一个两位数,与它相邻的11的整数倍的数为它的“邻居数”,与它最接近的“邻居数”为“最佳邻居数”,m的“最佳邻居数”记作n,令;
若m为一个三位数,它的“邻居数”则为111的整数倍,依次类推.
例如:50的“邻居数”为44与55,,,
∵,∴55为50的“最佳邻居数”,∴,
再如:492的“邻居数”为444和555,,,
∵,∴444是492的“最佳邻居数”.
(1)求和的值;
(2)若p为一个两位数,十位数字为a,个位数字为b,且.求p的值.
4、新型冠状病毒肺炎在全球蔓延,口罩成了人们生活中的必备物资.某口罩厂现安排A、B两组工人共150人加工口罩,A组工人每人每小时可加工口罩70个,B组工人每人每小时可加工口罩50个,A、B两组工人每小时一共可加工口罩9300个.试问:A、B两组工人各多少人?
5、今年(2022年)4月20日,是云大附中建校95周年暨云大附中恢复办学40周年校庆日,我校初一年级数学兴趣小组的小明同学发现这样一个有趣的巧合;小明的爸爸和爷爷都是云附的老校友,且爸爸和妹妹的年龄差恰好与爷爷和小明的年龄差的和为95,而爸爸的年龄恰好比爷爷的年龄小40.已知小明今年13岁,妹妹今年4岁.
(1)求今年小明的爸爸和爷爷的年龄分别是多少岁?(要求用二元一次方程组解答)
(2)假如小明的爸爸和爷爷都是15岁初中华业的,请问小明的爸爸和爷爷分别是哪一年毕业的云附学子?
6、材料阅读:一个各个数位上数字均不相同且都不为0的四位自然数N,将其千位上数字与十位上数字之和记为x,百位上数字与个位上数字之和记为y,若x﹣y=1.且其千位上数字与个位上数字之和等于百位上数字,则称N为“扬一数”.例如:N=2573,x=2+7=9,y=5+3=8,x﹣y=1,2+3=5则2573是“扬一数”;再如N=2354,x=2+5=7,y=3+4=7,x﹣y=0≠1,所以2354不是“扬一数”.
(1)请判断4652和4157,是不是“扬一数”,并说明理由;
(2)已知一个四位数S是“扬一数”,且能被7整除,请求出所有满足条件的S.
班级:________ 姓名:________
一、单选题(共 10 小题)
1、《九章算术》有个题目,大意是:“五只雀、六只燕,共重16两,雀重燕轻,互换其中一只,恰好一样重.”设每只雀、燕的重量分别为x两,y两,可得方程组是( )
A. B.
C. D.
2、请阅读下面的诗句:“栖树一群鸦,鸦树不知数.三只栖一树,五只没处去.五只栖一树,闲了一棵树.请你仔细数,鸦树各几何?”若设鸦有只,树有棵,则可列方程组为( )
A. B.
C. D.
3、“某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的 A、B 两种长方体形状的无盖纸盒.现 有正方形纸板 120 张,长方形纸板 360 张,刚好全部用完,问能做成多少个 A 型盒子?”则下列结论 正确的个数是( )
①甲同学:设 A 型盒子个数为 x 个,根据题意可得: 4x 3 360
②乙同学:设 B 型盒中正方形纸板的个数为 m 个,根据题意可得: 3 4(120 m) 360
③A 型盒 72 个
④B 型盒中正方形纸板 48 个
A.1 B.2 C.3 D.4
4、在“幻方拓展课程”探索中,小明在如图的3×3方格内填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则x﹣y=( )
A.2 B.4 C.6 D.8
5、我国古代数学名著《算法统宗》中记载:“今有绫七尺, 罗九尺,共价适等; 只云罗每尺价比绫每尺少钱三十六文,问各钱价若干 ” 意思是: 现在有一匹7尺长的绫布和一匹9 尺长的罗布恰好一样贵,只知道每尺罗布比绫布便宜36文,问两种布每尺各多少钱 设绫布每尺文,罗布每尺文,那么可列方程组为( )
A. B. C. D.
6、古代一歌谣:栖树一群鸦,鸦树不知数:三个坐一棵,五个地上落;五个坐一棵,闲了一棵树.意思就是说,有一群乌鸦要到树林休息,如果每棵树上落坐有三只乌鸦,则有五个落在地上;如果每棵树上落坐有五只乌鸦,则有一棵树没有乌鸦落坐,请你动脑筋,鸦树各几何?若设乌鸦有x只,树有y棵,由题意可列方程组( )
A. B. C. D.
7、某公司用3000元购进两种货物,货物卖出后,一种货物的利润率是10%,另一种货物的利润率是11%,两种货物共获利315元,如果设该公司购进这两和货物所用的费用分别为x元,y元,则列出的方程组是( )
A. B.
C. D.
8、在某场CBA比赛中,某位运动员的技术统计如下表所示:
技术 上场时间(分钟) 出手投篮(次) 投中(次) 罚球得分(分) 篮板(个) 防攻(次) 个人总得分(分)
数据 38 27 11 6 3 4 33
注:①表中出手投篮次数和投中次数均不包括罚球;
②总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,本场比赛中该运动员投中两分球和三分球各( )个.
A.5,6 B.6,5 C.4,7 D.7,4
9、某校组织一批学生去研学,若单独租用45座新能源客车若干辆,则有15人没有座位;若单独租用35座新能源客车,则用车数量将增加2辆,并空出15个座位.现在要求同时租用 45座和35座两种车型的新能源客车,既保证每人有座位,又保证每辆车不空座位,则需45座和35座两种车型的数量分别为( )
A.3辆、2辆 B.2辆、3辆 C.1辆、4辆 D.4辆、1辆
10、如图为某快餐店促销活动的内容,某同学到该快餐店购 买相差4元的2种快餐各1份,结账时,店员说:你多买2瓶指定饮料,按促销活动优惠价的金额,和你只买2份快餐的金额一样,这位同学想了想说:我还是只多买 1 瓶指定饮料吧,要求你以最便宜的方式给我结账,这位同学要付的金额是( )
A.56 B.57 C.58 D.60
二、填空题(共 10 小题)
1、母亲节来临之际,某花店购进大量的康乃馨、百合、玫瑰,打算采用三种不同方式搭配成花束,分别是“心之眷恋”、 “佳人如兰”、“守候”.已知销售每束“心之眷恋”的利润率为10%,每束“佳人如兰”的利润率为20%,每束“守候”的利润率为30%,当售出的三种花束数量之比为2:3:4时,商人得到的总利润率为25%:当售出的三种花束数量之比为3:2:1时,商人得到的总利润率为20%,那么当售出的三种花束数量之比为1:3:1时,这个商人得到的总利润率为______.
2、《九章算术》第七卷“盈不足"中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何 ”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少 ”则物价为_______.
3、幻方的历史很悠久,传说最早出现在夏禹时代的“洛书”.把洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在3×3(三行三列)的方格中,如果满足每个横行、每个竖列、每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的方格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则mn=_____.
4、一个三位数,百位上的数字是 ,如果把“”移到个位,其他两个数字及顺序均不变,所得的新三位数比原三位数的2倍少7,原来的三位数是____.
5、为积极响应教育部对中小学生实行“五项管理”之读物管理,某书店购进了大量的文史类、科普类、生活类读物,每类读物进价分别是12元,10元,8元.同类读物的标价相同,且科普类和生活类读物的标价一样,该书店对这三类读物全部打6折销售.若每类读物的销量相同,则书店不亏不赚,此时生活类读物利润率为.若文史类、科普类、生活类销量之比是,则书店销售这三类读物的总利润率为_____.(利润率)
6、某体育场的环形跑道长400m,甲 乙分别以一定的速度练习长跑和自行车,如果反向而行,他们每隔30s相遇一次.如果同向而行,那么每隔80s乙就追上甲一次.则甲的速度是________m/s.
7、《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来就是 类似地,图2所示的算筹图我们可以用方程组形式表述为__________.
8、学校计划购买和两种品牌的足球,已知一个品牌足球60元,一个品牌足球75元.学校准备将1500元钱全部用于购买这两种足球(两种足球都买),该学校的购买方案共有_________种.
9、为了开展“阳光体育”活动,某班计划购买甲、乙两种体育用品每种体育用品都购买,其中甲种体育用品每件20元,乙种体育用品每件30元,共用去150元,请你设计一下,共有______种购买方案.
10、某商场购进商品后,加价40%作为销售价.五一期间,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款448元.两种商品原销售价之和为560元.则两种商品进价分别为________元.
三、解答题(共 6 小题)
1、某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.若购买这两类球的总金额为4600元,则篮球、足球各买了多少个?
2、目前,新型冠状病毒在我国虽可控可防,但不可松懈某校欲购置规格分别为和的甲、乙两种免洗手消毒液若干瓶,已知购买1瓶甲和1瓶乙免洗手消毒液需要32元,购5瓶甲和3瓶乙免洗手消毒液需要120元.
(1)求甲、乙两种免洗手消毒液的单价.
(2)该校在校师生共1000人,平均每人每天都需使用的免洗手消毒液,若校方采购甲、乙两免洗手消毒液共花费4000元,则这批消毒液可使用多少天?
(3)为节约成本,该校购买散装免洗手消毒液进行分装,现需将的免洗手消毒液全部装入最大容量分别为和的两种空瓶中(每瓶均装满),若分装时平均每瓶需损耗,请问如何分装能使总损耗最小,求出此时需要的两种空瓶的数量.
3、若m是一个两位数,与它相邻的11的整数倍的数为它的“邻居数”,与它最接近的“邻居数”为“最佳邻居数”,m的“最佳邻居数”记作n,令;
若m为一个三位数,它的“邻居数”则为111的整数倍,依次类推.
例如:50的“邻居数”为44与55,,,
∵,∴55为50的“最佳邻居数”,∴,
再如:492的“邻居数”为444和555,,,
∵,∴444是492的“最佳邻居数”.
(1)求和的值;
(2)若p为一个两位数,十位数字为a,个位数字为b,且.求p的值.
4、新型冠状病毒肺炎在全球蔓延,口罩成了人们生活中的必备物资.某口罩厂现安排A、B两组工人共150人加工口罩,A组工人每人每小时可加工口罩70个,B组工人每人每小时可加工口罩50个,A、B两组工人每小时一共可加工口罩9300个.试问:A、B两组工人各多少人?
5、今年(2022年)4月20日,是云大附中建校95周年暨云大附中恢复办学40周年校庆日,我校初一年级数学兴趣小组的小明同学发现这样一个有趣的巧合;小明的爸爸和爷爷都是云附的老校友,且爸爸和妹妹的年龄差恰好与爷爷和小明的年龄差的和为95,而爸爸的年龄恰好比爷爷的年龄小40.已知小明今年13岁,妹妹今年4岁.
(1)求今年小明的爸爸和爷爷的年龄分别是多少岁?(要求用二元一次方程组解答)
(2)假如小明的爸爸和爷爷都是15岁初中华业的,请问小明的爸爸和爷爷分别是哪一年毕业的云附学子?
6、材料阅读:一个各个数位上数字均不相同且都不为0的四位自然数N,将其千位上数字与十位上数字之和记为x,百位上数字与个位上数字之和记为y,若x﹣y=1.且其千位上数字与个位上数字之和等于百位上数字,则称N为“扬一数”.例如:N=2573,x=2+7=9,y=5+3=8,x﹣y=1,2+3=5则2573是“扬一数”;再如N=2354,x=2+5=7,y=3+4=7,x﹣y=0≠1,所以2354不是“扬一数”.
(1)请判断4652和4157,是不是“扬一数”,并说明理由;
(2)已知一个四位数S是“扬一数”,且能被7整除,请求出所有满足条件的S.
