17.1.2勾股定理应用
文档属性
| 名称 | 17.1.2勾股定理应用 |

|
|
| 格式 | zip | ||
| 文件大小 | 589.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-07 00:00:00 | ||
图片预览




文档简介
课件19张PPT。2014年3月5日17.1.2 勾股定理的应用回顾与思考 1、直角三角形的三边之间分别存在着什么数量关系?2、勾股定理的用途有哪些?勾股定理:
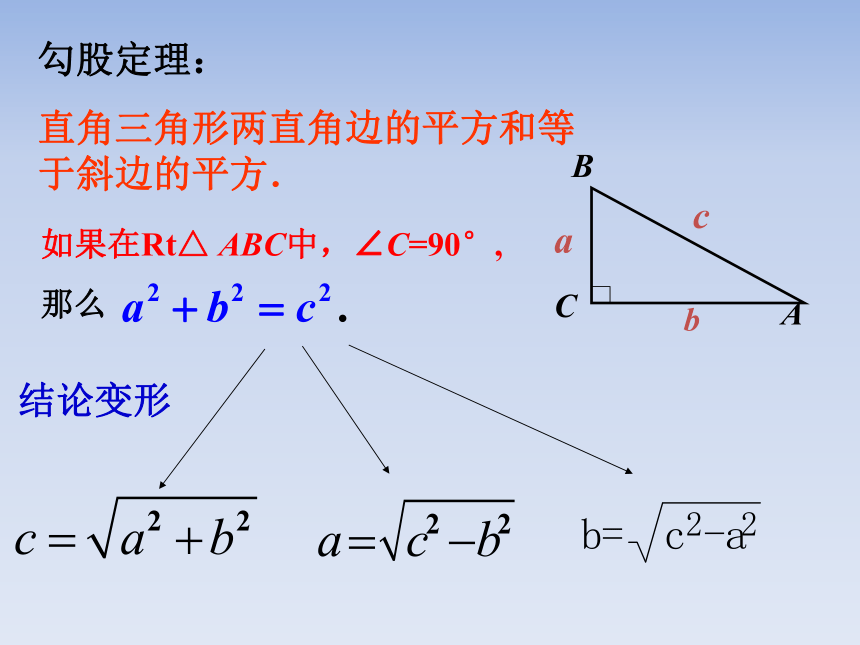
直角三角形两直角边的平方和等于斜边的平方.如果在Rt△ ABC中,∠C=90°,
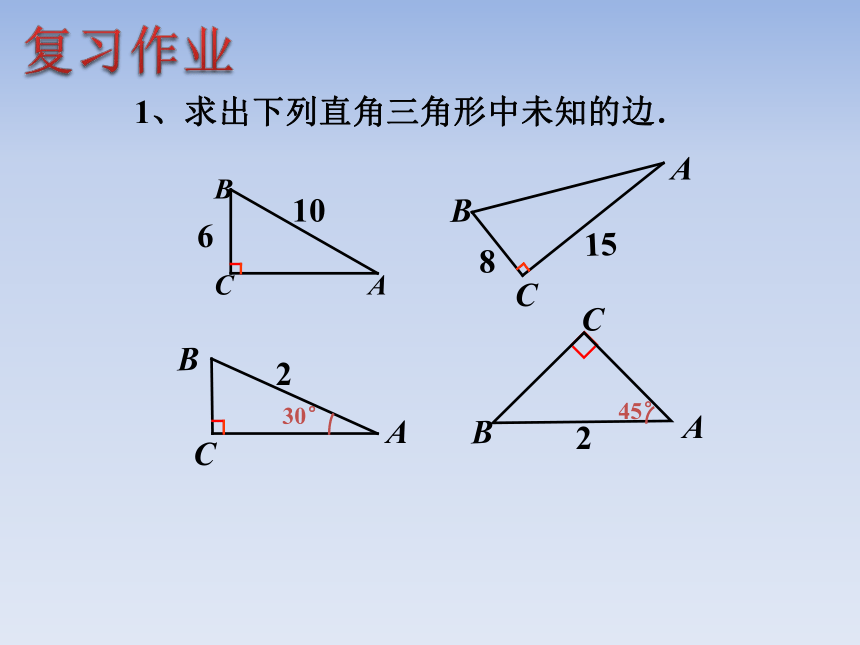
那么结论变形1、求出下列直角三角形中未知的边.ACBACB复习作业2、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
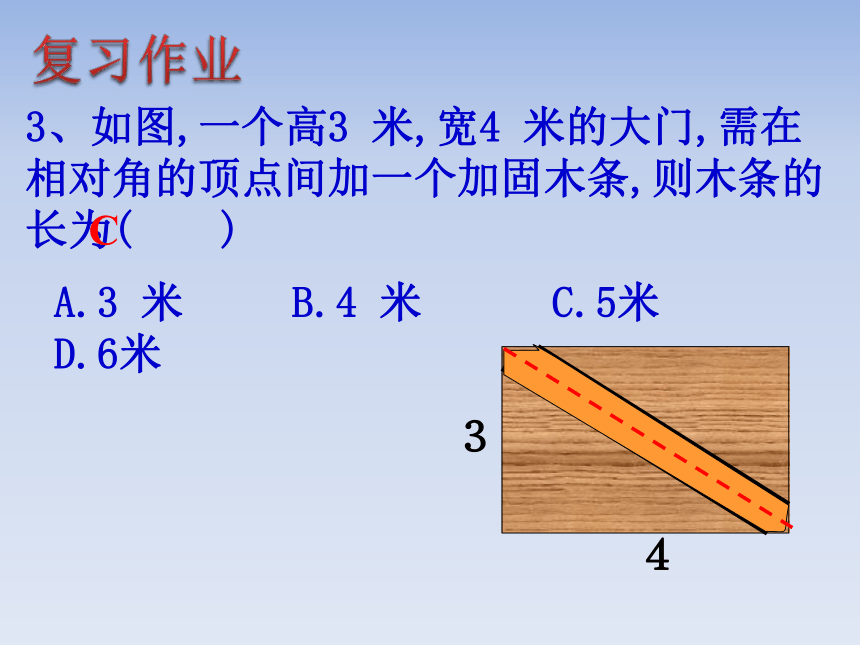
××复习作业3、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )A.3 米 B.4 米 C.5米 D.6米C34复习作业4、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )2、4、6C 4、6、8BB 6、8、10D 8、10、12复习作业 5.如图,所有的三角形都是直角三角形,四边形
都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积. 复习作业勾股定理应用 例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么? 解:在Rt△ABC中,根据勾股
定理,得 AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,所以
木板能从门框内通过.练习1:如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB= 60m,AC= 20m ,你能求出A、B两点间的距离吗? (结果保留整数) 例2 如图,一架2.6米长的梯子AB 斜靠在一竖直
的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,
那么梯子底端B也外移0.5米吗?勾股定理应用引申:一架梯子AB 斜靠在一竖直的墙AO上,这时AO为2.4米,当梯子的顶端A沿墙下滑0.5米时,梯子底端B也外移0.5米.求梯子的长度. 如果知道平面直角坐标系坐标轴上任意两点
的坐标为(x,0),(0,y),你能求这两点之间的
距离吗? 1. 完成课本第26页”练习”第2题.想一想巩固练习 巩固练习 2.如图,一棵树被台风吹折断后,树顶端落在离底
端3米处,测得折断后长的一截比短的一截长1米,你能
计算树折断前的高度吗?1.如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离.提高作业2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49提高作业3.小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕,发现屏幕只有58厘米长和46厘米宽.他觉得一定是售货员搞错了,你同意他的想法吗?你能解释这是为什么吗?提高作业 4.做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.提高作业这节课你学到了什么?再见
直角三角形两直角边的平方和等于斜边的平方.如果在Rt△ ABC中,∠C=90°,
那么结论变形1、求出下列直角三角形中未知的边.ACBACB复习作业2、判断题:
1)直角三角形三边分别为 a, b, c ,则一定满足下面的式子: a2+b2 =c2( )
2) 直角三角形的两边长分别是3和4,则第三边长是5.
( )
××复习作业3、如图,一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木条,则木条的长为( )A.3 米 B.4 米 C.5米 D.6米C34复习作业4、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )2、4、6C 4、6、8BB 6、8、10D 8、10、12复习作业 5.如图,所有的三角形都是直角三角形,四边形
都是正方形,已知正方形A,B,C,D 的边长分别是12,16,9,12.求最大正方形E 的面积. 复习作业勾股定理应用 例1 一个门框的尺寸如图所示,一块长3 m,宽
2.2 m的长方形薄木板能否从门框内通过?为什么? 解:在Rt△ABC中,根据勾股
定理,得 AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,所以
木板能从门框内通过.练习1:如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB= 60m,AC= 20m ,你能求出A、B两点间的距离吗? (结果保留整数) 例2 如图,一架2.6米长的梯子AB 斜靠在一竖直
的墙AO上,这时AO 为2.4米.
(1)求梯子的底端B距墙角O多少米?
(2)如果梯子的顶端A沿墙下滑0.5米,
那么梯子底端B也外移0.5米吗?勾股定理应用引申:一架梯子AB 斜靠在一竖直的墙AO上,这时AO为2.4米,当梯子的顶端A沿墙下滑0.5米时,梯子底端B也外移0.5米.求梯子的长度. 如果知道平面直角坐标系坐标轴上任意两点
的坐标为(x,0),(0,y),你能求这两点之间的
距离吗? 1. 完成课本第26页”练习”第2题.想一想巩固练习 巩固练习 2.如图,一棵树被台风吹折断后,树顶端落在离底
端3米处,测得折断后长的一截比短的一截长1米,你能
计算树折断前的高度吗?1.如图:是一个长方形零件图,根据所给的尺寸,求两孔中心A、B之间的距离.提高作业2.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49提高作业3.小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电视机的屏幕,发现屏幕只有58厘米长和46厘米宽.他觉得一定是售货员搞错了,你同意他的想法吗?你能解释这是为什么吗?提高作业 4.做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.提高作业这节课你学到了什么?再见
