2.2.1 直线与平面平行的判定 课件(共23张PPT)
文档属性
| 名称 | 2.2.1 直线与平面平行的判定 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
1.将铅笔放在桌面上,此时铅笔与桌面有无数多个公共点;
2.抬起铅笔的一端,此时铅笔与桌面只有1个公共点;
3.把铅笔放到文具盒(文具盒在桌面上)上面,铅笔与桌面就没有公共点了.
新课导入
直线
与平面
有无穷多个公共点时,直线
在平面
内,其图形如(1).
如果一条直线与一个平面只有一个公共点,那么就称这条直线与这个平面相交,
画直线与平面相交的图形,要把直线延伸到平行四边形外(如图(2)).
如果一条直线与一个平面没有公共点,那么就称这条直线与这个平面平行.直线
平行,记作
∥
l与平面
.画直线与平面平行的图形,要把直线画在平行四边形
外,并与平行四边形的一边平行(如图9 19(3)).
l
l
l
新课导入
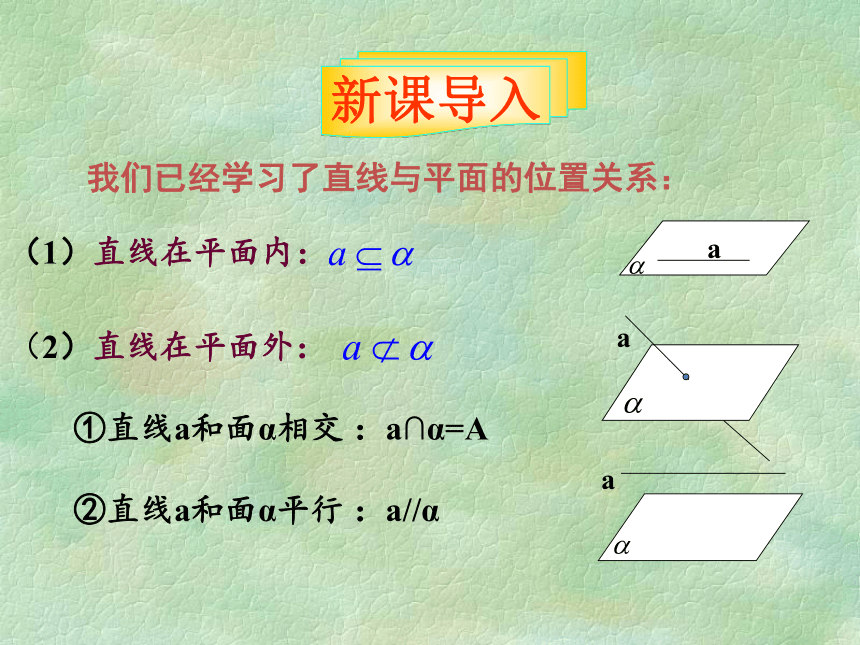
(1)直线在平面内:
(2)直线在平面外:
①直线a和面α相交 :a∩α=A
a
a
a
②直线a和面α平行 :a//α
我们已经学习了直线与平面的位置关系:
在直线与平面的关系中,平行是一种非常重要的关系,它应用很多,而且是学习面与面平行的基础。
如何判定直线与平面平行呢?
根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.
但是,直线无限延长,平面无限延展,如何保证直线与平面没有公共点呢?
2.2.1 直线与平面平行的判定
在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.
问题
实例感受
观察
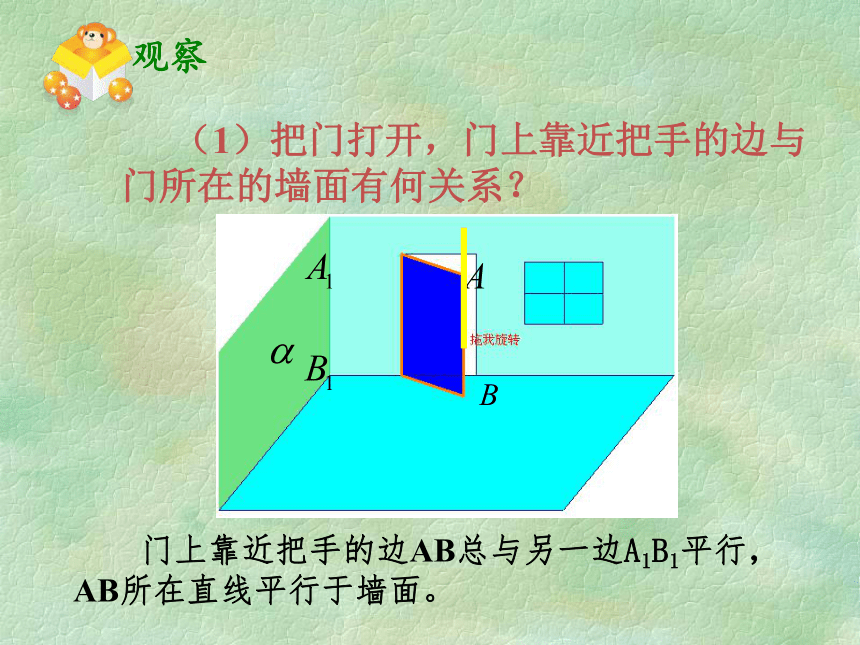
(1)把门打开,门上靠近把手的边与门所在的墙面有何关系?
门上靠近把手的边AB总与另一边A1B1平行,AB所在直线平行于墙面。
观察
实例感受
将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
书页无论怎样翻动,书页边缘与桌面不可能相交,所以AB所在直线平行于桌面所在平面。
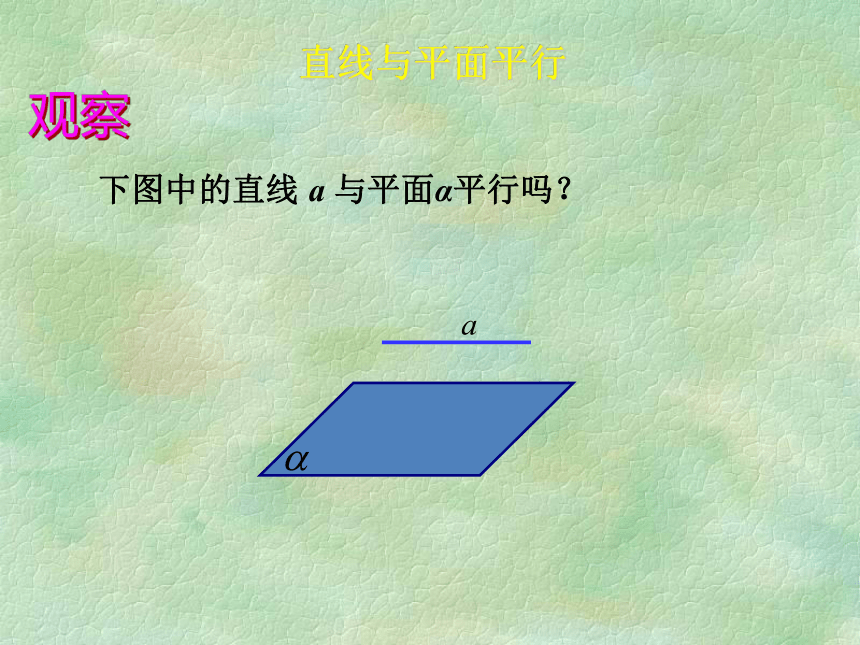
下图中的直线 a 与平面α平行吗?
观察
直线与平面平行
平面α外有直线 a平行于平面α内的直线 b。
(1)这两条直线共面吗?
(2)直线a 与平面α相交吗?
共面
不可能相交
探究
直线和平面平行的判定定理:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
符号表示:
简述为:
线线平行,则线面平行
注意:使用定理时,必须具备三个条件:
(1)直线a在平面α外
(2)直线b在平面α内
(3)两条直线a、b平行
三个条件缺一不可,缺少其中任何一条,则结论就不一定成立了。
面外
面内
平行
巩固知识 典型例题
例2 如图长方体 中,直线 平行于
平面 吗?为什么?
(1)定义法:证明直线与平面无公共点;
(2)判定定理:证明平面外直线与平面内直线平行.
小结:直线与平面平行判定
怎样判定直线与平面平行?
创设情境 兴趣导入
活动:
将铅笔放到与桌面平行的位置,用矩形硬纸片的面紧贴铅笔,矩形硬纸片的一边紧贴桌面(如图),观察铅笔及硬纸片与桌面的交线,发现它们是平行的.
铅笔
直线和平面平行的性质定理:
如果一条直线与一个平面平行,并且经过这条直线的平面和这个平面相交,那么这条直线与交线平行。
符号表示:
面面相交、线面平行 线线平行
作用:
判定直线与直线平行的重要依据。
关键:
寻找平面与平面的交线。
如图所示的一块木料中,棱BC//平面A'C',
BC//B'C',要经过面A'C'内的一点P和棱BC将木料锯开,应该怎样画线?
例3
A
A′
C
B
D
P
D′
B′
C′
课堂小结
1.直线与平面平行的判定:
2.直线与平面平行的性质:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
如果一条直线与一个平面平行,并且经过这条直线的平面和这个平面相交,那么这条直线与交线平行。
随堂练习
2.直线a∥平面α,平面α内有无数条直线交于一点,那么这无数条直线中与直线a平行的( )
A. 至少有一条 B. 至多有一条
C.有且只有一条 D.不可能有
C
B
1.直线 a∥平面α,平面α内有 n 条互相平行的直线,那么这 n 条直线和直线a( )
A. 全平行 B. 全异面
C. 全平行或全异面 D. 不全平行也不全异面
3.下列命题是否正确,并说明理由
(1)过平面外一点有无数条直线与这个平面平行( )
(2)过直线外一点可以作无数个平面与已知直线平行( )
例2、如图,在正方体ABCD——A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.
M
N
M
习题答案
2.
平行于平面AEC。
1.(1)平面A'B'C'D'平面CC'D'D
(2)平面B'BCC'平面CC'D'D
(3)平面A'B'C'D'平面B'BCC'
1.将铅笔放在桌面上,此时铅笔与桌面有无数多个公共点;
2.抬起铅笔的一端,此时铅笔与桌面只有1个公共点;
3.把铅笔放到文具盒(文具盒在桌面上)上面,铅笔与桌面就没有公共点了.
新课导入
直线
与平面
有无穷多个公共点时,直线
在平面
内,其图形如(1).
如果一条直线与一个平面只有一个公共点,那么就称这条直线与这个平面相交,
画直线与平面相交的图形,要把直线延伸到平行四边形外(如图(2)).
如果一条直线与一个平面没有公共点,那么就称这条直线与这个平面平行.直线
平行,记作
∥
l与平面
.画直线与平面平行的图形,要把直线画在平行四边形
外,并与平行四边形的一边平行(如图9 19(3)).
l
l
l
新课导入
(1)直线在平面内:
(2)直线在平面外:
①直线a和面α相交 :a∩α=A
a
a
a
②直线a和面α平行 :a//α
我们已经学习了直线与平面的位置关系:
在直线与平面的关系中,平行是一种非常重要的关系,它应用很多,而且是学习面与面平行的基础。
如何判定直线与平面平行呢?
根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.
但是,直线无限延长,平面无限延展,如何保证直线与平面没有公共点呢?
2.2.1 直线与平面平行的判定
在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.
问题
实例感受
观察
(1)把门打开,门上靠近把手的边与门所在的墙面有何关系?
门上靠近把手的边AB总与另一边A1B1平行,AB所在直线平行于墙面。
观察
实例感受
将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
书页无论怎样翻动,书页边缘与桌面不可能相交,所以AB所在直线平行于桌面所在平面。
下图中的直线 a 与平面α平行吗?
观察
直线与平面平行
平面α外有直线 a平行于平面α内的直线 b。
(1)这两条直线共面吗?
(2)直线a 与平面α相交吗?
共面
不可能相交
探究
直线和平面平行的判定定理:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
符号表示:
简述为:
线线平行,则线面平行
注意:使用定理时,必须具备三个条件:
(1)直线a在平面α外
(2)直线b在平面α内
(3)两条直线a、b平行
三个条件缺一不可,缺少其中任何一条,则结论就不一定成立了。
面外
面内
平行
巩固知识 典型例题
例2 如图长方体 中,直线 平行于
平面 吗?为什么?
(1)定义法:证明直线与平面无公共点;
(2)判定定理:证明平面外直线与平面内直线平行.
小结:直线与平面平行判定
怎样判定直线与平面平行?
创设情境 兴趣导入
活动:
将铅笔放到与桌面平行的位置,用矩形硬纸片的面紧贴铅笔,矩形硬纸片的一边紧贴桌面(如图),观察铅笔及硬纸片与桌面的交线,发现它们是平行的.
铅笔
直线和平面平行的性质定理:
如果一条直线与一个平面平行,并且经过这条直线的平面和这个平面相交,那么这条直线与交线平行。
符号表示:
面面相交、线面平行 线线平行
作用:
判定直线与直线平行的重要依据。
关键:
寻找平面与平面的交线。
如图所示的一块木料中,棱BC//平面A'C',
BC//B'C',要经过面A'C'内的一点P和棱BC将木料锯开,应该怎样画线?
例3
A
A′
C
B
D
P
D′
B′
C′
课堂小结
1.直线与平面平行的判定:
2.直线与平面平行的性质:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
如果一条直线与一个平面平行,并且经过这条直线的平面和这个平面相交,那么这条直线与交线平行。
随堂练习
2.直线a∥平面α,平面α内有无数条直线交于一点,那么这无数条直线中与直线a平行的( )
A. 至少有一条 B. 至多有一条
C.有且只有一条 D.不可能有
C
B
1.直线 a∥平面α,平面α内有 n 条互相平行的直线,那么这 n 条直线和直线a( )
A. 全平行 B. 全异面
C. 全平行或全异面 D. 不全平行也不全异面
3.下列命题是否正确,并说明理由
(1)过平面外一点有无数条直线与这个平面平行( )
(2)过直线外一点可以作无数个平面与已知直线平行( )
例2、如图,在正方体ABCD——A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.
M
N
M
习题答案
2.
平行于平面AEC。
1.(1)平面A'B'C'D'平面CC'D'D
(2)平面B'BCC'平面CC'D'D
(3)平面A'B'C'D'平面B'BCC'
