2.3.2平面与平面垂直的判定 课件(共23张PPT)
文档属性
| 名称 | 2.3.2平面与平面垂直的判定 课件(共23张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 539.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 07:16:49 | ||
图片预览





文档简介
(共23张PPT)
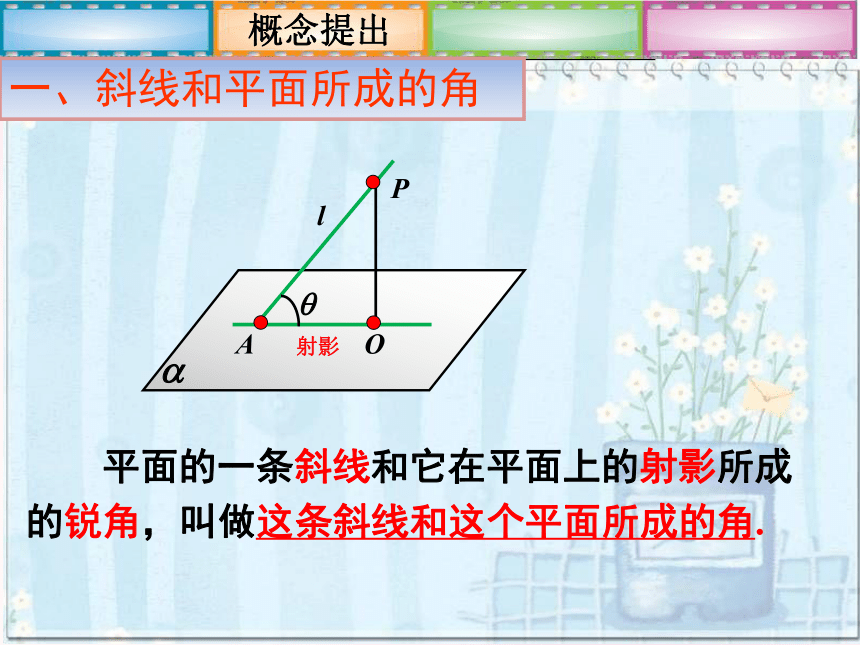
平面的一条斜线和它在平面上的射影所成的锐角,叫做这条斜线和这个平面所成的角.
斜线和平面所成的角
概念提出
一、斜线和平面所成的角
P
A
O
l
射影
问题1:空间平行关系有哪几种?
直线与直线平行
直线与平面平行
平面与平面平行
问题2:前面我们学过的空间垂直关系有哪几种?
直线与直线垂直
直线与平面垂直
平面与平面垂直
问题3:前面我们学过的空间的角有哪几种?
两条异面直线
所成的角
直线和平面
所成的角
平面与平面
所成的角
新课导入
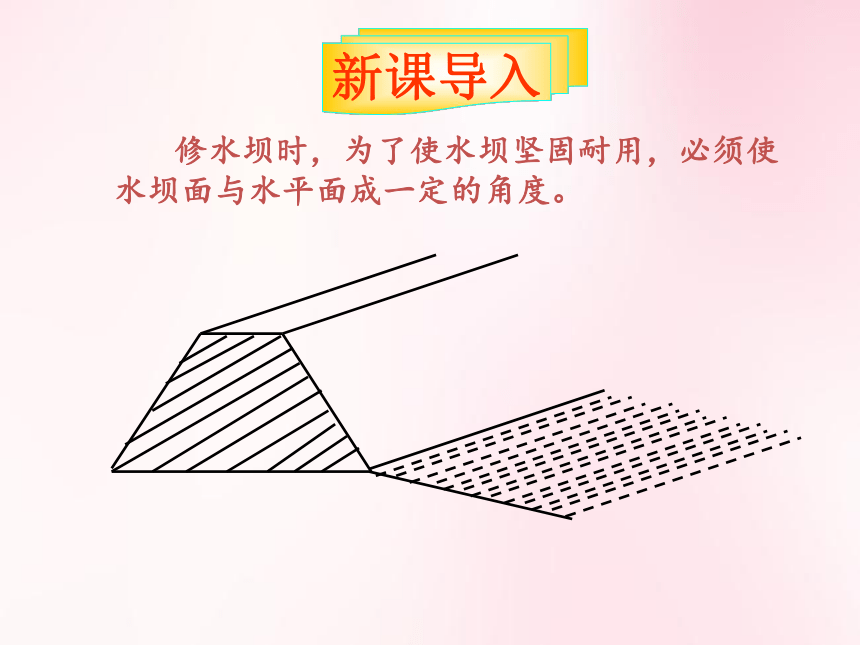
修水坝时,为了使水坝坚固耐用,必须使水坝面与水平面成一定的角度。
砌墙时,要保证墙面与地面垂直。
B
A
C
D
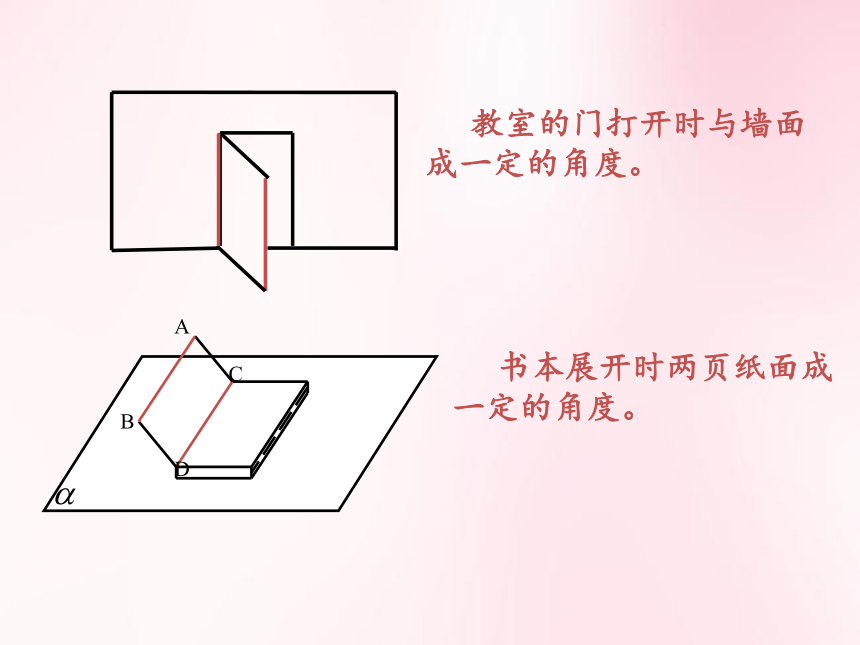
教室的门打开时与墙面成一定的角度。
书本展开时两页纸面成一定的角度。
2.3.2平面与平面垂直的判定
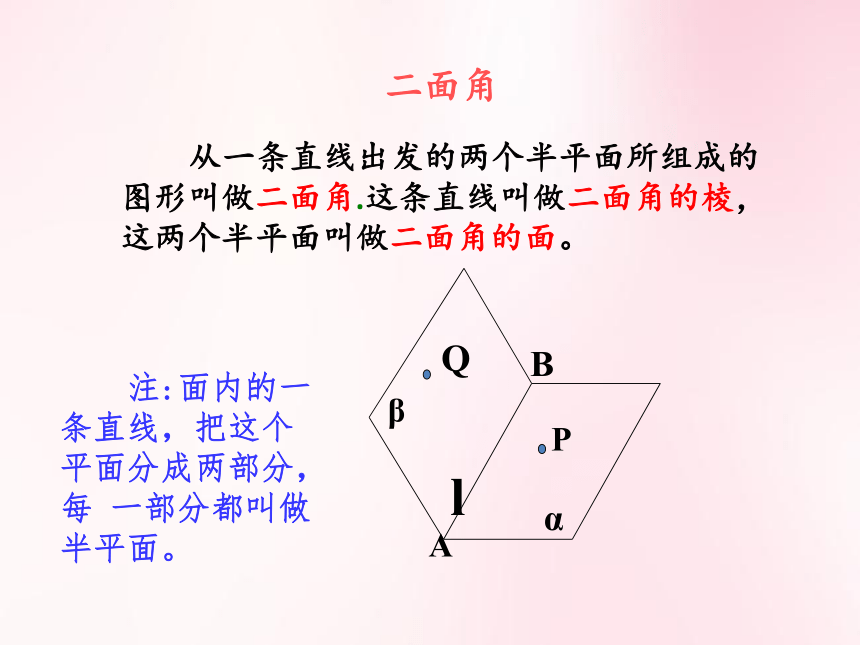
从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
二面角
注:面内的一条直线,把这个平面分成两部分,每 一部分都叫做半平面。
二面角的记法
下图二面角记做 二面角α-l-β,或二面角α-AB-β。
用面1-棱-面2表示一个二面角
有时为了方便,在α,β内分别取点P,Q,将此二面角记做P-l-Q,或二面角P-AB-Q。
l
β
α
A
B
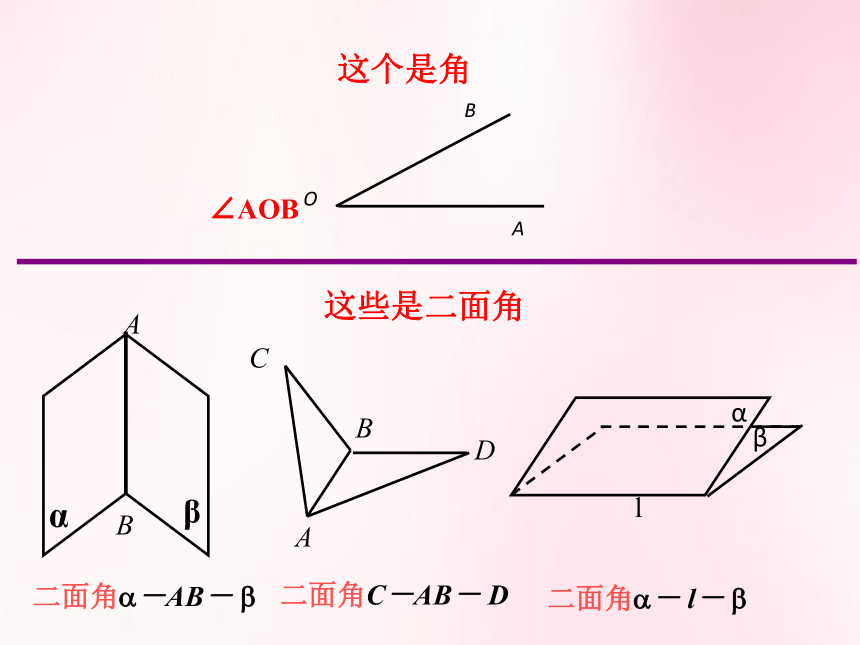
二面角 -AB-
二面角 - l-
二面角C-AB- D
A
B
C
D
O
B
A
∠AOB
这个是角
这些是二面角
角
A
B
从一点出发的两条射线所组成的图形叫做角。
定义
构成
边—顶点—边
表示法
∠AOB
二面角
从一条直线出发的两个半平面所组成的图形叫做二面角。
面—棱—面
二面角 —l—
或二面角P—l—Q
图形
角与二面角的类比
l
.
顶点
棱
边
边
面
面
O
.
.
Q
.
P
提示:异面直线所成的角、直线和平面所成的角
也是空间角,它们的大小是如何刻画的?
(转化成平面角)
问题1:我们如何刻画二面角的大小?
在二面角 —l— 的棱l上任取一点O,以点O为垂足,在半平面 和 内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角。
.
o
A
B
二面角的平面角的特点:
3)角的边都要垂直于二面角的棱.
1)角的顶点在棱上;
2)角的两边分别在两个面内;
10
l
O
A
B
A
O
B
质疑一:角的两边为什么要垂直于棱?
二面角的平面角具有唯一性
质疑二:在二面角的平面角的定义中O点是在棱上任取的,那么∠AOB的大小与点O在棱上的位置有关系吗?
A
B
A’
B’
二面角的平面角大小与点O在棱上的位置无关,只与二面角的张角大小有关。
结论:二面角是用它的平面角来度量的,一个二面角的平面角多大,就说这个二面角是多少度的二面角。
练习:教室相邻的两个墙面与地面可以构成二面角吗?分别指出构成这些 二面角的面、棱、平面角及其度数。
.
动脑思考 探索新知
当二面角的两个半平面重合时,规定二面角为零角;当二面角的两个半平面合成一个平面时,规定二面角为平角.因此二面角取值范围是
.
平面角是直角的二面角叫做直二面角.例如教室的墙壁与地面就组成直二面角,此时称两个平面垂直.平面 与平面 垂直记作
一般地,两个平面相交,如果它们所成的二面
角是直二面角,就说这两个平面互相垂直.
平面与平面垂直的定义:
β
α
α
β
图形表示
记作:α⊥β
平面角是直角的二面角叫做直二面角。
思考:给出两个相交平面,如何判 断它们是否垂直。
如果一个平面经过另一个平面的
垂线,那么这两个平面互相垂直。
平面与平面垂直的判定定理
符号表示:
简记:线面垂直,则面面垂直。
练习1:
A
C
B
D
A1
C1
B1
D1
如图为正方体,请问哪些平面与 垂直
平面和平面垂直的性质定理
如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
A
O
B
符号表示:
面面垂直
线面垂直
课堂小结
从一条直线引出的两个半平面所组成的图形叫做二面角。二面角的平面角用来度量二面角的大小。
平面角是直角的二面角叫做直二面角。
平面和平面垂直的判定定理:
如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直。
A
B
D
C
线面垂直
面面垂直
平面的一条斜线和它在平面上的射影所成的锐角,叫做这条斜线和这个平面所成的角.
斜线和平面所成的角
概念提出
一、斜线和平面所成的角
P
A
O
l
射影
问题1:空间平行关系有哪几种?
直线与直线平行
直线与平面平行
平面与平面平行
问题2:前面我们学过的空间垂直关系有哪几种?
直线与直线垂直
直线与平面垂直
平面与平面垂直
问题3:前面我们学过的空间的角有哪几种?
两条异面直线
所成的角
直线和平面
所成的角
平面与平面
所成的角
新课导入
修水坝时,为了使水坝坚固耐用,必须使水坝面与水平面成一定的角度。
砌墙时,要保证墙面与地面垂直。
B
A
C
D
教室的门打开时与墙面成一定的角度。
书本展开时两页纸面成一定的角度。
2.3.2平面与平面垂直的判定
从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面。
二面角
注:面内的一条直线,把这个平面分成两部分,每 一部分都叫做半平面。
二面角的记法
下图二面角记做 二面角α-l-β,或二面角α-AB-β。
用面1-棱-面2表示一个二面角
有时为了方便,在α,β内分别取点P,Q,将此二面角记做P-l-Q,或二面角P-AB-Q。
l
β
α
A
B
二面角 -AB-
二面角 - l-
二面角C-AB- D
A
B
C
D
O
B
A
∠AOB
这个是角
这些是二面角
角
A
B
从一点出发的两条射线所组成的图形叫做角。
定义
构成
边—顶点—边
表示法
∠AOB
二面角
从一条直线出发的两个半平面所组成的图形叫做二面角。
面—棱—面
二面角 —l—
或二面角P—l—Q
图形
角与二面角的类比
l
.
顶点
棱
边
边
面
面
O
.
.
Q
.
P
提示:异面直线所成的角、直线和平面所成的角
也是空间角,它们的大小是如何刻画的?
(转化成平面角)
问题1:我们如何刻画二面角的大小?
在二面角 —l— 的棱l上任取一点O,以点O为垂足,在半平面 和 内分别作垂直于棱l的射线OA和OB,则射线OA和OB构成的∠AOB叫做二面角的平面角。
.
o
A
B
二面角的平面角的特点:
3)角的边都要垂直于二面角的棱.
1)角的顶点在棱上;
2)角的两边分别在两个面内;
10
l
O
A
B
A
O
B
质疑一:角的两边为什么要垂直于棱?
二面角的平面角具有唯一性
质疑二:在二面角的平面角的定义中O点是在棱上任取的,那么∠AOB的大小与点O在棱上的位置有关系吗?
A
B
A’
B’
二面角的平面角大小与点O在棱上的位置无关,只与二面角的张角大小有关。
结论:二面角是用它的平面角来度量的,一个二面角的平面角多大,就说这个二面角是多少度的二面角。
练习:教室相邻的两个墙面与地面可以构成二面角吗?分别指出构成这些 二面角的面、棱、平面角及其度数。
.
动脑思考 探索新知
当二面角的两个半平面重合时,规定二面角为零角;当二面角的两个半平面合成一个平面时,规定二面角为平角.因此二面角取值范围是
.
平面角是直角的二面角叫做直二面角.例如教室的墙壁与地面就组成直二面角,此时称两个平面垂直.平面 与平面 垂直记作
一般地,两个平面相交,如果它们所成的二面
角是直二面角,就说这两个平面互相垂直.
平面与平面垂直的定义:
β
α
α
β
图形表示
记作:α⊥β
平面角是直角的二面角叫做直二面角。
思考:给出两个相交平面,如何判 断它们是否垂直。
如果一个平面经过另一个平面的
垂线,那么这两个平面互相垂直。
平面与平面垂直的判定定理
符号表示:
简记:线面垂直,则面面垂直。
练习1:
A
C
B
D
A1
C1
B1
D1
如图为正方体,请问哪些平面与 垂直
平面和平面垂直的性质定理
如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
A
O
B
符号表示:
面面垂直
线面垂直
课堂小结
从一条直线引出的两个半平面所组成的图形叫做二面角。二面角的平面角用来度量二面角的大小。
平面角是直角的二面角叫做直二面角。
平面和平面垂直的判定定理:
如果一个平面过另一个平面的一条垂线,那么这两个平面互相垂直。
A
B
D
C
线面垂直
面面垂直
