【2023春人教版八下数学优质备课】16.1.2二次根式的性质 课件(共21张PPT)
文档属性
| 名称 | 【2023春人教版八下数学优质备课】16.1.2二次根式的性质 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 09:55:34 | ||
图片预览








文档简介
(共21张PPT)
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十六章 二次根式
16.1二次根式
第2课时 二次根式的性质
经历探索性质 = a(a≥0)和 = a(a≥0)的过程,并理解其意义;
核心素养目标:
会运用性质 = a(a≥0)和 = a(a≥0)进行二次根式的化简;
理解二次根式的非负性,会利用二次根式的非负性解决相关问题.
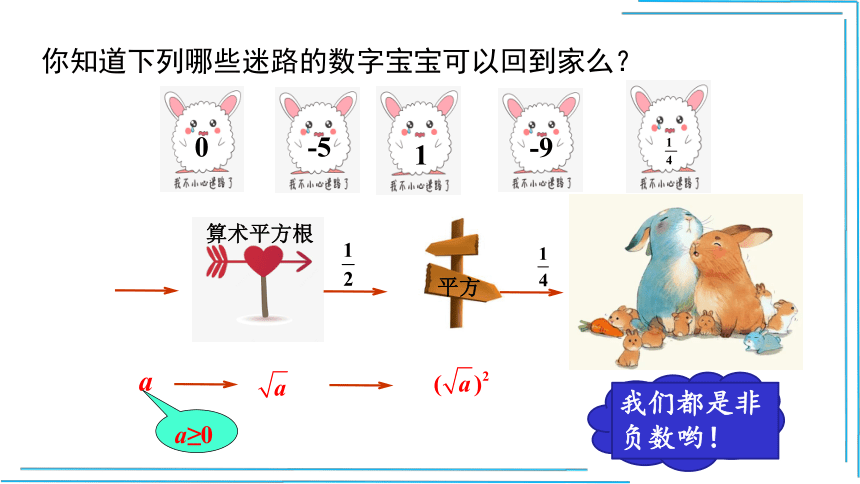
算术平方根
平方
0
-5
-9
a
a≥0
1
我们都是非负数哟!
你知道下列哪些迷路的数字宝宝可以回到家么?
1.二次根式的定义:
2.二次根式的性质:
交流回顾:
形如式子叫做二次根式。
4
2
0
1 根据算数平方根的意义填空
互助探究:
是2的算术平方根,根据算术平方根的意义, 是一个平方等于2的非负数.
归纳总结:
一般地, =a (a ≥0).
(2)用到了
(ab)2=a2b2这个
结论.
例题讲解:
例
3.
分析:我们可以直接利用。
解:=,==95=45,=
跟踪训练:
计算下列各式的值:
=18, =
=-30
0.1
2
0
2 填空
互助探究:
归纳总结:
一般地,根据算术平方根的意义有
例2:化简
解:(1)=5
例题讲解:
想一想:如何化简 呢?
=|a|
a
-a
=
(a≥ 0);
(a<0).
跟踪训练:
化简下列各式:
(1)(2)(3) (4) (a<0)
解:
(1)
(2)=0.5
(3)
(4)
用基本运算符号(包括加、减、乘、除、乘方和开方)把_ 或 连接起来的式子,我们称这样的式子为代数式.
数
表示数的字母
想一想:初中阶段所学的代数式主要有哪几类?
代数式定义:
代数式
整式
分式
二次根式
分层训练:
【题型一】利用=|a|、=a进行计算
化简:(1) (4)
解析:根据二次根式的性质进行计算即可.
解:(1)=5;=5
方法总结:利用=|a|进行计算与化简,幂的运算法则仍然适用,同时要注意二次根式的被开方数要为非负数.
分层训练:
解析:由于任意一个非负数都可以写成一个数的平方的形式,利用这个即可将以上几个式子在实数范围内分解因式.
解:(1)-13=-=(a+)(a-);
(2)4-5=-=(2a+)(2a-);
(3)-4+4===
方法总结:一些式子在有理数的范围内无法分解因式,可是在实数范围内就可以继续分解因式.这就需要把一个非负数表示成平方的形式.
【题型二】 =a(a≥0)的有关应用
在实数范围内分解因式.
(1)a2-13;(2)4a2-5;(3)x4-4x2+4.
课堂小结:
二次根式性质
性质1=a0
性质=a0
代数式的定义
课堂检测:
运算顺序
平方
开根号
平方
算数平方根
开根号
平方
算数平方根
平方
a
a
a
0
-a
绝对值
分类讨论
a的绝对值
与有什么区别?
1.这两个式子的________ 不同.
计算要先________,再________,也就是求a________的________.
计算要先________,再________,也就是求a ________ 的________.
如何化简,它有什么性质?
2.化简(a,=__ _=_____.化简后等于________.
如何化简,它有什么性质?
3.第一步:变成________形式,将变成________.
第二步:________.
4化简二次根式:=________=
5利用的性质化简(a<0变成绝对值形式:
去绝对值:
≥2
<2
-a+b=2b=2d
课后作业:
1.必做题:
教材P.5习题16.1第2、4题.
2.选做题:
教材P.5习题16.1第7、8、9题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
交流预习
2023春人教版八(下)数学同步精品课件
核心素养目标
复习引入
互助探究
例题精讲
跟踪训练
分层提高
课堂小结
知识自测
课后作业
第十六章 二次根式
16.1二次根式
第2课时 二次根式的性质
经历探索性质 = a(a≥0)和 = a(a≥0)的过程,并理解其意义;
核心素养目标:
会运用性质 = a(a≥0)和 = a(a≥0)进行二次根式的化简;
理解二次根式的非负性,会利用二次根式的非负性解决相关问题.
算术平方根
平方
0
-5
-9
a
a≥0
1
我们都是非负数哟!
你知道下列哪些迷路的数字宝宝可以回到家么?
1.二次根式的定义:
2.二次根式的性质:
交流回顾:
形如式子叫做二次根式。
4
2
0
1 根据算数平方根的意义填空
互助探究:
是2的算术平方根,根据算术平方根的意义, 是一个平方等于2的非负数.
归纳总结:
一般地, =a (a ≥0).
(2)用到了
(ab)2=a2b2这个
结论.
例题讲解:
例
3.
分析:我们可以直接利用。
解:=,==95=45,=
跟踪训练:
计算下列各式的值:
=18, =
=-30
0.1
2
0
2 填空
互助探究:
归纳总结:
一般地,根据算术平方根的意义有
例2:化简
解:(1)=5
例题讲解:
想一想:如何化简 呢?
=|a|
a
-a
=
(a≥ 0);
(a<0).
跟踪训练:
化简下列各式:
(1)(2)(3) (4) (a<0)
解:
(1)
(2)=0.5
(3)
(4)
用基本运算符号(包括加、减、乘、除、乘方和开方)把_ 或 连接起来的式子,我们称这样的式子为代数式.
数
表示数的字母
想一想:初中阶段所学的代数式主要有哪几类?
代数式定义:
代数式
整式
分式
二次根式
分层训练:
【题型一】利用=|a|、=a进行计算
化简:(1) (4)
解析:根据二次根式的性质进行计算即可.
解:(1)=5;=5
方法总结:利用=|a|进行计算与化简,幂的运算法则仍然适用,同时要注意二次根式的被开方数要为非负数.
分层训练:
解析:由于任意一个非负数都可以写成一个数的平方的形式,利用这个即可将以上几个式子在实数范围内分解因式.
解:(1)-13=-=(a+)(a-);
(2)4-5=-=(2a+)(2a-);
(3)-4+4===
方法总结:一些式子在有理数的范围内无法分解因式,可是在实数范围内就可以继续分解因式.这就需要把一个非负数表示成平方的形式.
【题型二】 =a(a≥0)的有关应用
在实数范围内分解因式.
(1)a2-13;(2)4a2-5;(3)x4-4x2+4.
课堂小结:
二次根式性质
性质1=a0
性质=a0
代数式的定义
课堂检测:
运算顺序
平方
开根号
平方
算数平方根
开根号
平方
算数平方根
平方
a
a
a
0
-a
绝对值
分类讨论
a的绝对值
与有什么区别?
1.这两个式子的________ 不同.
计算要先________,再________,也就是求a________的________.
计算要先________,再________,也就是求a ________ 的________.
如何化简,它有什么性质?
2.化简(a,=__ _=_____.化简后等于________.
如何化简,它有什么性质?
3.第一步:变成________形式,将变成________.
第二步:________.
4化简二次根式:=________=
5利用的性质化简(a<0
去绝对值:
≥2
<2
-a+b=2b=2d
课后作业:
1.必做题:
教材P.5习题16.1第2、4题.
2.选做题:
教材P.5习题16.1第7、8、9题.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
