苏科版八年级数学下册 9.10 三角形的中位线同步练习【拔尖特训】(含解析)
文档属性
| 名称 | 苏科版八年级数学下册 9.10 三角形的中位线同步练习【拔尖特训】(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 748.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览


文档简介
9.10三角形的中位线(重难点培优30题)
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、单选题
1.(2022春·江苏南通·八年级统考期末)如图,DE是的中位线,若DE=3,则BC的长为( )
A.4 B.5 C.6 D.8
2.(2022春·江苏·八年级专题练习)如图,平行四边形中,对角线,交于点O,点E是的中点.若,则的长为( )
A. B. C. D.
3.(2022春·江苏·八年级专题练习)如图,在四边形中,,,、、分别是、、的中点,若,,则等于( )
A.76° B.56° C.38° D.28°
4.(2022春·江苏徐州·八年级统考期中)若四边形的对角线互相垂直,那么顺次连结该四边形中点所得的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.以上都不对
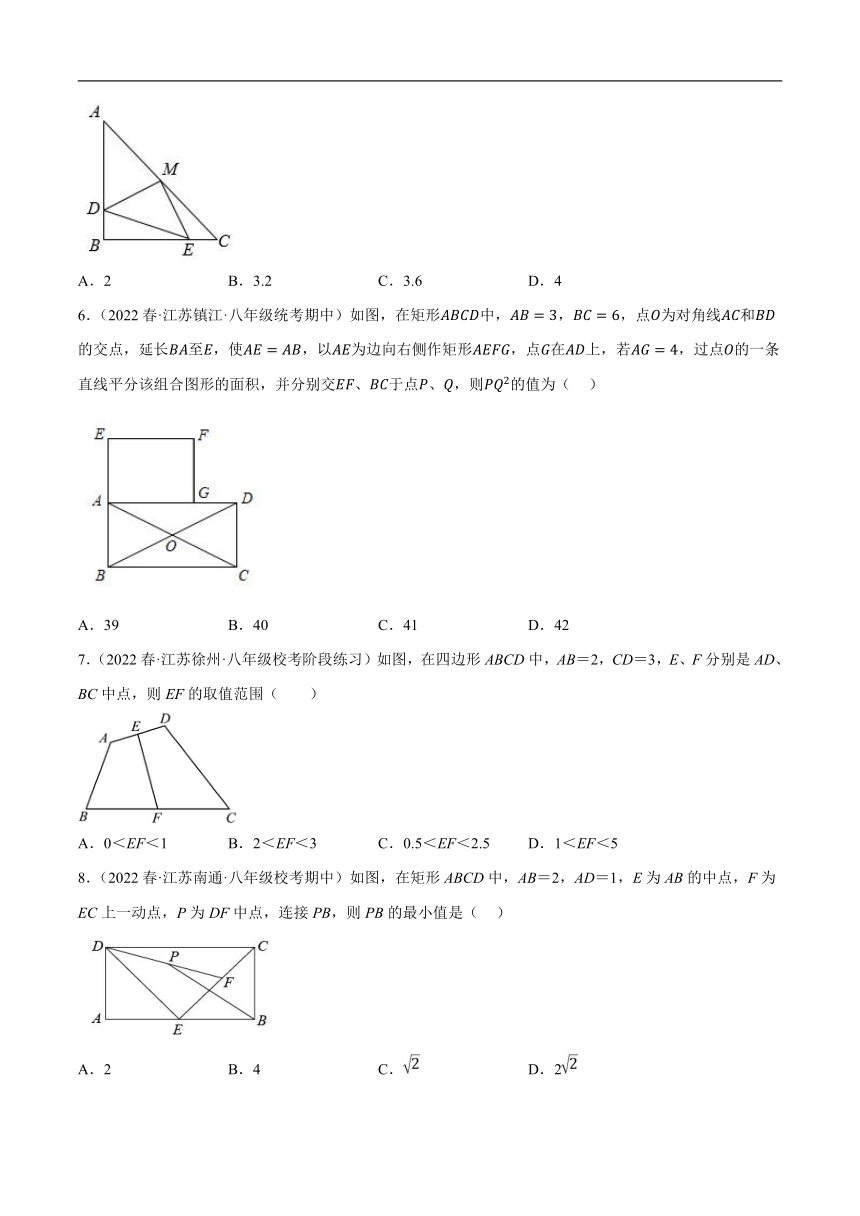
5.(2022秋·江苏无锡·八年级无锡市天一实验学校校考阶段练习)如图,在中,,,M是AC的中点,D、E分别在AB、BC上,且,则四边形的面积为( )
A.2 B.3.2 C.3.6 D.4
6.(2022春·江苏镇江·八年级统考期中)如图,在矩形中,,,点为对角线和的交点,延长至,使,以为边向右侧作矩形,点在上,若,过点的一条直线平分该组合图形的面积,并分别交、于点、,则的值为( )
A.39 B.40 C.41 D.42
7.(2022春·江苏徐州·八年级校考阶段练习)如图,在四边形ABCD中,AB=2,CD=3,E、F分别是AD、BC中点,则EF的取值范围( )
A.0<EF<1 B.2<EF<3 C.0.5<EF<2.5 D.1<EF<5
8.(2022春·江苏南通·八年级校考期中)如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
A.2 B.4 C. D.2
二、填空题
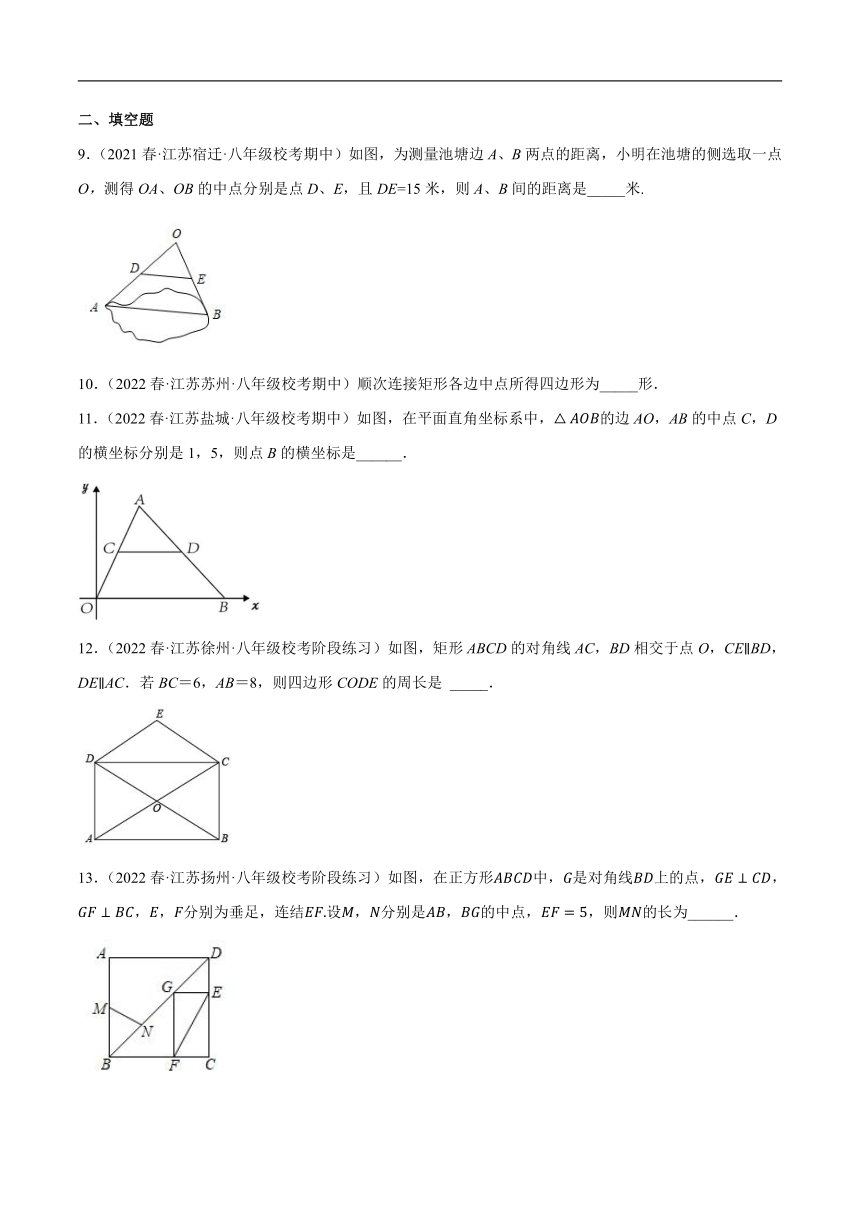
9.(2021春·江苏宿迁·八年级校考期中)如图,为测量池塘边A、B两点的距离,小明在池塘的侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=15米,则A、B间的距离是_____米.
10.(2022春·江苏苏州·八年级校考期中)顺次连接矩形各边中点所得四边形为_____形.
11.(2022春·江苏盐城·八年级校考期中)如图,在平面直角坐标系中,的边AO,AB的中点C,D的横坐标分别是1,5,则点B的横坐标是______.
12.(2022春·江苏徐州·八年级校考阶段练习)如图,矩形ABCD的对角线AC,BD相交于点O,CEBD,DEAC.若BC=6,AB=8,则四边形CODE的周长是 _____.
13.(2022春·江苏扬州·八年级校考阶段练习)如图,在正方形中,是对角线上的点,,,,分别为垂足,连结设,分别是,的中点,,则的长为______.
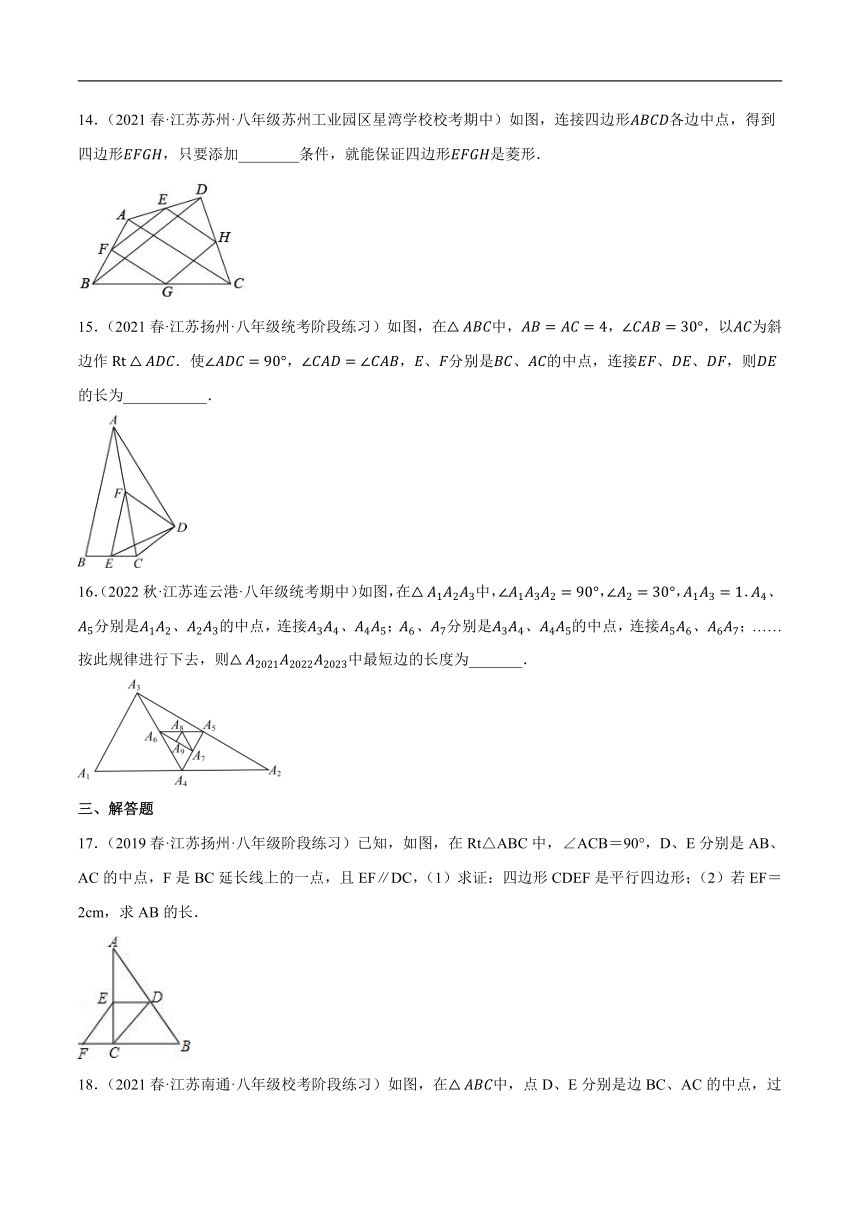
14.(2021春·江苏苏州·八年级苏州工业园区星湾学校校考期中)如图,连接四边形各边中点,得到四边形,只要添加________条件,就能保证四边形是菱形.
15.(2021春·江苏扬州·八年级统考阶段练习)如图,在中,,,以为斜边作.使,,、分别是、的中点,连接、、,则的长为___________.
16.(2022秋·江苏连云港·八年级统考期中)如图,在中,,,.分别是的中点,连接;分别是的中点,连接;……按此规律进行下去,则中最短边的长度为_______.
三、解答题
17.(2019春·江苏扬州·八年级阶段练习)已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC,(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
18.(2021春·江苏南通·八年级校考阶段练习)如图,在中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当满足什么条件时,四边形图ADCF是菱形?为什么?
19.(2021春·江苏宿迁·八年级校考期中)如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?并说明理由.
20.(2020秋·江苏苏州·八年级校联考阶段练习)如图,△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.
(1)求证:MD=ME;
(2)若D为AB的中点,且AB=10,求ME的长.
21.(2022春·江苏盐城·八年级校考期中)在菱形中,两条对角线相交于点,是边的中点,连接并延长到,使,连接,.
(1)求证:四边形是矩形;
(2)求证:.
22.(2022春·江苏泰州·八年级校考阶段练习)如图,在□ABCD中,点E是AB边的中点,
(1)仅用一把无刻度的直尺画出CD边的中点F;
(2)在(1)的条件下,求证:EF=BC.
23.(2022春·江苏无锡·八年级校考阶段练习)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别是AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2.
①求∠BMN的度数;
②求BN的长.
24.(2022春·江苏泰州·八年级统考期末)如图1,D、E、F分别是各边上的点,四边形ADEF是平行四边形,有三个选项:①D是AB的中点,②E是BC的中点,③F是AC的中点.
(1)请从三个选项中选择两个作为条件,余下一个作为结论,并证明.
你选择的条件是______,结论是______(填序号);
(2)在(1)的条件下,如图2,点H在BC上,,连接DH、FH,
①若,求的度数;
②若,,连接DF,的面积为S,直接写出S的取值范围.
答案与解析
一、单选题
1.(2022春·江苏南通·八年级统考期末)如图,DE是的中位线,若DE=3,则BC的长为( )
A.4 B.5 C.6 D.8
【答案】C
【分析】根据三角形中位线的性质即可求解.
【详解】解:∵DE是的中位线,DE=3,
∴BC=6.
故选:C.
【点睛】本题考查了三角形中位线的性质,掌握中位线的性质是解题的关键.
2.(2022春·江苏·八年级专题练习)如图,平行四边形中,对角线,交于点O,点E是的中点.若,则的长为( )
A. B. C. D.
【答案】D
【分析】根据平行四边形的性质,可得出点O平分AC,则OE是三角形ABC的中位线,则AB=2OE,继而求出答案.
【详解】解:∵四边形ABCD为平行四边形,
∴AO=CO,
∵点E是CB的中点,
∴OE为△ABC的中位线,
∴AB=2OE,
∵OE=6cm ,
∴AB=12cm.
故选:D.
【点睛】本题考查了平行四边形的性质和三角形的中位线定理,关键是根据平行四边形的性质得出OE为△ABC的中位线.
3.(2022春·江苏·八年级专题练习)如图,在四边形中,,,、、分别是、、的中点,若,,则等于( )
A.76° B.56° C.38° D.28°
【答案】D
【分析】利用、分别是和两个三角形的中位线,求出,从而得出和,再根据,利用三角形内角和定理即可求出的度数.
【详解】解:∵、、分别是、、的中点,
∴、分别是和两个三角形的中位线,
∴,,且,
∴,,
∴,
又∵,
∴.
故本题答案为:D.
【点睛】本题考查了三角形内角和定理,等腰三角形的判定与性质,三角形中位线定理.解决本题的关键是正确理解题意,熟练掌握三角形中位线定理,通过等腰三角形的性质找到相等的角.
4.(2022春·江苏徐州·八年级统考期中)若四边形的对角线互相垂直,那么顺次连结该四边形中点所得的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.以上都不对
【答案】A
【分析】根据三角形的中位线定理首先可以证明:顺次连接四边形各边中点所得四边形是平行四边形.再根据对角线互相垂直,即可证明平行四边形的一个角是直角,则有一个角是直角的平行四边形是矩形.
【详解】解:如图,E、F、G、H分别是AB、BC、CD、AD的中点,
∴EHFGBD,EH=FGBD;EFHGAC,EF=HGAC,
∴四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EH⊥EF,∠HEF=90°
∴四边形EFGH是矩形.
故选:A.
【点睛】此题主要考查了三角形中位线定理、平行四边形的判定、矩形的判定等知识,熟练掌握三角形的中位线定理是解题的关键.
5.(2022秋·江苏无锡·八年级无锡市天一实验学校校考阶段练习)如图,在中,,,M是AC的中点,D、E分别在AB、BC上,且,则四边形的面积为( )
A.2 B.3.2 C.3.6 D.4
【答案】D
【分析】连接BM, 根据三线合一可得,进而证明,,证明,根据即可求解.
【详解】解:如图,连接BM,
∵在中,,,M是AC的中点,
∴,
∵在中,,,,
∴,,
∴,
∴(ASA),
,
∴ ,
∴.
故选D.
【点睛】本题考查了等腰三角形的性质,全等三角形的性质与判定,证明是解题的关键.
6.(2022春·江苏镇江·八年级统考期中)如图,在矩形中,,,点为对角线和的交点,延长至,使,以为边向右侧作矩形,点在上,若,过点的一条直线平分该组合图形的面积,并分别交、于点、,则的值为( )
A.39 B.40 C.41 D.42
【答案】B
【分析】根据题意可得PQ必过矩形EFGA的对角线交点,连接AF,EG交于点H,取AE的中点M,AB的中点N,连接HM,ON,过点H作HT⊥ON于T,设PQ与AD的交点为S,根据三角形中位线定理可得,∠ANO=∠ABC=90°,,∠AMH=90°,再由勾股定理可得OH的长,再证明△ASO≌△CQO,可得SO=OQ,即可求解.
【详解】解:∵过点O的一条直线平分该组合图形的面积,
∴PQ必过矩形EFGA的对角线交点,
连接AF,EG交于点H,取AE的中点M,AB的中点N,连接HM,ON,过点H作HT⊥ON于T,设PQ与AD的交点为S,
∵四边形ABCD是矩形,
∴AO=CO,
又∵点N是AB的中点,
∴,ON∥BC,
∴∠ANO=∠ABC=90°,
同理:,∠AMH=90°,
∵HT⊥NO,
∴四边形MHTN为矩形,
∴MH=NT=2,MT=MN=3,
∴TO=1,
∴,
∵AD∥BC,
∴∠DAC=∠BCA,∠ASO=∠CQO,
在△ASO和△CQO中,
∵,
∴△ASO≌△CQO(AAS),
∴SO=OQ,
同理PH=SH,
∴,
∴.
故选:B
【点睛】本题考查了矩形的性质,三角形中位线定理,全等三角形的判定和性质,勾股定理,灵活运用这些性质解决问题是本题的关键.
7.(2022春·江苏徐州·八年级校考阶段练习)如图,在四边形ABCD中,AB=2,CD=3,E、F分别是AD、BC中点,则EF的取值范围( )
A.0<EF<1 B.2<EF<3 C.0.5<EF<2.5 D.1<EF<5
【答案】C
【分析】根据三角形中位线定理求出EH、FH,根据三角形的三边关系计算即可.
【详解】解:连接AC,取AC的中点H,连接EH、FH,
∵AH=HC,AE=ED,
∴EH=CD=1.5,
同理,FH=AB=1,
在Rt△EHF中,EH﹣FH<EF<EH+FH,即0.5<EF<2.5,
故选:C.
【点睛】本题考查的是三角形中位线定理、三角形的三边关系,根据三角形中位线定理求出EH、FH是解题的关键.
8.(2022春·江苏南通·八年级校考期中)如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
A.2 B.4 C. D.2
【答案】C
【分析】根据中位线定理可得出点P的运动轨迹是线段,再根据垂线段最短可得当BP⊥时,PB取得最小值,由矩形的性质以及已知的数据即可知BP1⊥,故BP的最小值为BP1的长,由勾股定理求解即可.
【详解】如图,
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴∥CE且=,
当点F在EC上除点C、E的位置处时有DP=FP,
由中位线定理可知:P1P∥CE且P1P= ,
∴当点P的运动轨迹是线段,
∴当BP⊥时,PB取得最小值,
∵矩形ABCD中,AB=2,AD=1,E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=1,
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°,
∴∠DP2P1=90°,
∴∠DP1P2=45°,
∴∠P2P1B=90°,即BP1⊥,
∴BP的最小值为BP1的长,
在等腰直角三角形BCP1中,CP1=BC=1,
∴BP1=,
∴PB的最小值是,
故选:C.
【点睛】本题考查轨迹问题、矩形的性质等知识,解题的关键是学会利用特殊位置解决问题.
二、填空题
9.(2021春·江苏宿迁·八年级校考期中)如图,为测量池塘边A、B两点的距离,小明在池塘的侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=15米,则A、B间的距离是_____米.
【答案】30
【分析】根据D、E是OA、OB的中点,即DE是△OAB的中位线,根据三角形的中位线定理:三角形的中位线平行于第三边且等于第三边的一半,即可求解.
【详解】解:∵D、E是OA、OB的中点,即DE是△OAB的中位线,
∴DE=AB,
∴AB=2DE=2×15=30米.
故答案为:30.
【点睛】本题考查了三角形的中位线定理应用,正确理解定理是解题的关键.
10.(2022春·江苏苏州·八年级校考期中)顺次连接矩形各边中点所得四边形为_____形.
【答案】菱
【分析】根据三角形的中位线定理和菱形的判定,顺次连接矩形各边中点所得的四边形是菱形
【详解】解:如图,连接AC、BD,
∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点,
∴EF=GH=AC,FG=EH=BD,
∵矩形ABCD的对角线AC=BD,
∴EF=GH=FG=EH,
∴四边形EFGH是菱形.
故答案为:菱.
【点睛】此题主要考查了三角形的中位线定理,矩形的性质和菱形的判定,综合利用了三角形的中位线定理和矩形的性质是解题关键.
11.(2022春·江苏盐城·八年级校考期中)如图,在平面直角坐标系中,的边AO,AB的中点C,D的横坐标分别是1,5,则点B的横坐标是______.
【答案】8
【分析】由C、D的横坐标求出线段CD的长度,结合中位线的定义和性质,得出OB的长度,从而得到B点的横坐标.
【详解】解:∵边AO,AB的中点为点C、D,
∴CD是△OAB的中位线,CDOB,
∵点C,D的横坐标分别是1,5,
∴CD=4,
∴OB=2CD=8,
∴点B的横坐标为8.
故答案为:8.
【点睛】本题主要考查了中位线定义和性质应用,解题的关键是由点C、D的横坐标求出线段CD的长度.
12.(2022春·江苏徐州·八年级校考阶段练习)如图,矩形ABCD的对角线AC,BD相交于点O,CEBD,DEAC.若BC=6,AB=8,则四边形CODE的周长是 _____.
【答案】20
【分析】由CEBD,DEAC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD=5,即可判定四边形CODE是菱形,继而求得答案.
【详解】解:∵CEBD,DEAC,
∴四边形CODE是平行四边形.
∵四边形ABCD是矩形,
∴AD=BC=6,OA=OC=OB=OD,∠BAD=90°,
∴,
∴OD=OC=AC=BD=5,
∴四边形CODE是菱形,
∴四边形CODE的周长为=4OC=4×5=20.
故答案为:20.
【点睛】本题考查了菱形的判定与性质以及矩形的性质,勾股定理.此题难度不大,注意证得四边形CODE是菱形是解答此题的关键.
13.(2022春·江苏扬州·八年级校考阶段练习)如图,在正方形中,是对角线上的点,,,,分别为垂足,连结设,分别是,的中点,,则的长为______.
【答案】2.5
【分析】如图所示。连接AG,CG,先证明△ABG≌△CBG(SSS),得到AG=CG,再证四边形ECFG是矩形,得到CG=EF=5,最后证明MN是△ABG的中位线,则.
【详解】解:如图所示。连接AG,CG,
∵四边形ABCD是正方形,
∴BA=BC,∠ABG=∠CBG,∠BCD=90°,
又∵BG=BG,
∴△ABG≌△CBG(SSS),
∴AG=CG,
∵GF⊥BC,GE⊥CD,∠ECF=90°,
∴四边形ECFG是矩形,
∴CG=EF=5,
∵M、N分别是AB,BG的中点,
∴MN是△ABG的中位线,
∴,
故答案为:2.5.
【点睛】本题主要考查了正方形的性质,全等三角形的性质与判定,矩形的性质与判定,三角形中位线定理,正确作出辅助线构造全等三角形是解题的关键.
14.(2021春·江苏苏州·八年级苏州工业园区星湾学校校考期中)如图,连接四边形各边中点,得到四边形,只要添加________条件,就能保证四边形是菱形.
【答案】
【分析】先证明中点四边形为平行四边形,则只需让一组邻边相等即可,而邻边都等于对角线的一半,那么添加对角线需相等即可.
【详解】解:添加时,四边形为菱形.
∵点E、F、G、H分别为、、、的中点,
∴,,,,,,
∴,,
∴四边形为平行四边形,
当时,,
∴四边形为菱形.
故答案为:.
【点睛】本题考查菱形的判定,三角形的中位线定理,解题的关键是熟悉菱形的判定定理,难度不大.
15.(2021春·江苏扬州·八年级统考阶段练习)如图,在中,,,以为斜边作.使,,、分别是、的中点,连接、、,则的长为___________.
【答案】
【分析】根据直角三角形的性质得到,根据三角形的外角性质得到,根据三角形中位线定理得到,,推出,利用勾股定理即可求解.
【详解】解:∵,F是的中点,
∴,
∴,
∴,
∵E、F分别是、的中点,
∴,,
∴,
∴,
∴.
故答案为:.
【点睛】本题考查的是直角三角形的性质、等腰三角形的性质、三角形外角的性质、三角形中位线定理,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.
16.(2022秋·江苏连云港·八年级统考期中)如图,在中,,,.分别是的中点,连接;分别是的中点,连接;……按此规律进行下去,则中最短边的长度为_______.
【答案】##
【分析】根据已知条件和图形的变化可得前几个图形中最短边的长度,找出规律,可得结论.
【详解】解:在中,,,,是的中点,
∴,
中最短边的边长为,
中最短边的边长为,
中最短边的边长为,
∴中最短边的边长为,
则中最短边的边长为,,
故答案为:.
【点睛】本题主要考查了规律型,图形的变化类,解决本题的关键是观察图形变化寻找规律.
三、解答题
17.(2019春·江苏扬州·八年级阶段练习)已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC,(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
【答案】(1)见解析;(2)4cm.
【分析】(1)根据三角形中位线定理可得ED∥FC;结合已知条件EF∥DC,即可得结论;
(2)根据直角三角形中,斜边上的中线等于斜边的一半得到AB=2DC.
【详解】(1)证明:如图,∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:由(1)知,四边形CDEF是平行四边形,则DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,
∴DC= AB,
∴AB=2DC=4cm.
故答案为(1)见解析;(2)4cm.
【点睛】本题考查平行四边形的判定与性质,直角三角形斜边上的中线.解题的关键是熟练掌握平行四边形的判定与性质以及直角三角形斜边上的中线等于斜边的一半.
18.(2021春·江苏南通·八年级校考阶段练习)如图,在中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当满足什么条件时,四边形图ADCF是菱形?为什么?
【答案】(1)见解析;(2)当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,理由见解析.
【分析】(1)首先利用平行四边形的判定方法得出四边形ABDF是平行四边形,进而得出AF=DC,利用一组对边相等且平行的四边形是平行四边形,进而得出答案;
(2)利用直角三角形的性质结合菱形的判定方法得出即可.
【详解】(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,BD=CD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)解:当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,
理由:∵△ABC是直角三角形,且∠BAC=90°
又∵点D是边BC的中点,
∴AD=DC,
∴平行四边形ADCF是菱形.
【点睛】本题考查平行四边形的判定与性质以及菱形的判定,熟练应用平行四边形的判定与性质是解题关键.
19.(2021春·江苏宿迁·八年级校考期中)如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?并说明理由.
【答案】(1)证明见解析
(2)OA=BC,理由见解析
【分析】(1)首先利用三角形中位线的性质得出DEBC,DE=BC,GFBC,GF=BC,从而得出DEGF,DE=GF,即可证得四边形DGFE是平行四边形;
(2)由四边形DGFE是菱形,可得DG=GF,再根据三角形中位线的性质可得DG=OA,GF=BC,从而得出OA=BC.
(1)
证明:∵D、E分别是边AB、AC的中点.
∴DEBC,DE=BC.
∵点G、F分别是OB、OC的中点,
∴GFBC,GF=BC.
∴DEGF,DE=GF.
∴四边形DEFG是平行四边形;
(2)
解:OA=BC,理由如下:
连接OA.
∵四边形DEFG是菱形,
∴DG=GF,
∵D是AB的中点,点G、F分别是OB、OC的中点,
∴DG=OA,GF=BC,
∴OA=BC.
【点睛】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,菱形的判定以及平行四边形与菱形的关系,熟记相关的定理和性质是解题的关键.
20.(2020秋·江苏苏州·八年级校联考阶段练习)如图,△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.
(1)求证:MD=ME;
(2)若D为AB的中点,且AB=10,求ME的长.
【答案】(1)见解析
(2)ME=5
【分析】(1)根据等腰三角形的性质求出∠B=∠C,求出BM=CM,根据全等三角形的判定得出△DBM≌△ECM,根据全等三角形的性质得出即可;
(2)根据三角形的中位线求出DM=AC,代入求出即可.
(1)
证明:∵AB=AC,
∴∠B=∠C,
∵M是BC的中点,
∴BM=CM,
在△DBM和△ECM中,
,
∴△DBM≌△ECM(SAS),
∴MD=ME;
(2)
解:∵M是BC的中点,D为AB的中点,
∴DM=AC,
∵AB=10,
∴AC=AB=10,
∴ME=DM=5.
【点睛】本题考查了全等三角形的性质和判定,三角形中位线的应用,能求出△DBM≌△ECM和DM=AC是解此题的关键.
21.(2022春·江苏盐城·八年级校考期中)在菱形中,两条对角线相交于点,是边的中点,连接并延长到,使,连接,.
(1)求证:四边形是矩形;
(2)求证:.
【答案】(1)见解析
(2)见解析
【分析】(1)由菱形ABCD可得出,由F是CD的中点、EF=OF,证四边形OCED是平行四边形,进而得出结论;
(2)证明是的中位线即可得出结论.
(1)
证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴,
∵是边的中点,
∴CF=DF,
又,
∴四边形OCED是平行四边形,
∵,
∴四边形OCED是矩形;
(2)
∵四边形是矩形,
∴,
∵四边形是菱形,
∴,
∴是的中位线,
∴.
【点睛】本题考查了菱形的性质,平行四边形的性质和判定,矩形的判定和性质,三角形中位线的性质,掌握以上知识是解题的关键.
22.(2022春·江苏泰州·八年级校考阶段练习)如图,在□ABCD中,点E是AB边的中点,
(1)仅用一把无刻度的直尺画出CD边的中点F;
(2)在(1)的条件下,求证:EF=BC.
【答案】(1)见详解
(2)见详解
【分析】(1)连接AC、BD,两者交于点G,连接EG并延长交CD与点F,即可.
(2)证明四边形ADFE是平行四边形即可.
(1)
作图如下:
点F即为所求,
证明:∵四边形ABCD是平行四边形,
∴,,CD=AB,对角线交点G平分对角线AC、BD,
∴点G为AC、BD的中点,
∵E点为AB中点,
∴EG为△ABD的中位线,
∴,即,
∵,
∴四边形ADFE是平行四边形,
∴AE=DF,
∵E点为AB中点,
∴,
∴,即有,
∴F点为DC中点,
即F点满足要求.
(2)
证明:在(1)中已证明有:四边形ADFE是平行四边形,
∴AD=EF,
∵AD=BC,
∴EF=BC,
结论得证.
【点睛】本题主要考查了基本作图,平行四边形的判定与性质、中位线的判定与性质等知识,掌握平行四边形的性质是解答本题的关键.注意作图只能用无刻度直尺,并非尺规作图.
23.(2022春·江苏无锡·八年级校考阶段练习)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别是AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2.
①求∠BMN的度数;
②求BN的长.
【答案】(1)答案见解析
(2)①∠BMN=90°;②BN=
【分析】(1)在△CAD中,由中位线定理得到MNAD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)①由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°,由平行线性质得到∠NMC=∠DAC=30°,故∠BMN=90°;②因为∠BMN=90°,由勾股定理得到,BN2=BM2+MN2,再由MN=BM=1,得到BN的长.
(1)
解:在△CAD中,∵M、N分别是AC、CD的中点,
∴MNAD,且MN=AD,
在Rt△ABC中,∵M是AC的中点,
∴BM=AC,
又∵AC=AD,
∴MN=BM;
(2)
①∵∠BAD=60°且AC平分∠BAD,
∴∠BAC=∠DAC=30°,
由(1)知,BM=AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MNAD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°;
②∵∠BMN=90°,
∴BN2=BM2+MN2,
而由(1)知,MN=BM=AC=×2=1,
∴BN=.
【点睛】本题考查了三角形中位线定理、直角三角形斜边中线定理、三角形的外角、勾股定理等知识,解题的关键是灵活应用三角形的中位线平行于第三边,并且等于第三边的一半.
24.(2022春·江苏泰州·八年级统考期末)如图1,D、E、F分别是各边上的点,四边形ADEF是平行四边形,有三个选项:①D是AB的中点,②E是BC的中点,③F是AC的中点.
(1)请从三个选项中选择两个作为条件,余下一个作为结论,并证明.
你选择的条件是______,结论是______(填序号);
(2)在(1)的条件下,如图2,点H在BC上,,连接DH、FH,
①若,求的度数;
②若,,连接DF,的面积为S,直接写出S的取值范围.
【答案】(1)①②;③
(2)①80°;②
【分析】(1)无论选哪两个作为条件,利用平行四边形的性质及三角形中位线性质定理,均可证明余下的那一个作为结论成立;
(2)①由直角三角形斜边上中线的性质、等腰三角形的性质即可求得结果;
②连接DF,由三角形中位线定理得DF∥BC,则,从而有,再由三角形的中线平分三角形面积知,由平行四边形可得,过点B作BM⊥AC于M,由垂线段最短可求得△ABC面积的最大值,从而可求得S的范围.
(1)
(1)选择条件①②,结论为③,证明如下:
∵D是AB的中点,E是BC的中点,
∴DE是△ABC的中位线,
∴,
∵四边形ADEF是平行四边形,
∴DE=AF,
∴,
∴F是AC的中点;
故答案为:①②,③;
同理可证:当①③为条件,②为结论;或②③为条件,①为结论;
(2)
①∵AH⊥BC,D为AB的中点,
∴DH为Rt△ABH斜边上的中线,
∴,
∴∠DAH=∠DHA;
同理:∠FAH=∠FHA,
∴∠DHF =∠DHA+∠FHA=∠DAH+∠FAH=∠BAC=180° (∠B+∠C)=80°;
②连接DF,如图,
∵D、F分别是AB、AC的中点,
∴DF是△ABC的中位线
∴DF//BC,
∴,
∴,
∵DH、FH分别是Rt△ABH、Rt△ACH斜边上的中线,
∴,,
∴,
∵四边形ADEF是平行四边形,
∴,
∴
∴
∴;
过点B作BM⊥AC于M,
则BM≤AB=8,
∴
即△ABC面积的最大值为40,
∴,
∵S>0,
∴S的范围为.
【点睛】本题考查了三角形中位线定理,直角三角形斜边上中线的性质,三角形中线平分三角形的面积的性质,平行四边形的性质,等腰三角形的性质,垂线段最短等知识,具有一定的综合性.灵活运用这些知识是解题的关键.
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、单选题
1.(2022春·江苏南通·八年级统考期末)如图,DE是的中位线,若DE=3,则BC的长为( )
A.4 B.5 C.6 D.8
2.(2022春·江苏·八年级专题练习)如图,平行四边形中,对角线,交于点O,点E是的中点.若,则的长为( )
A. B. C. D.
3.(2022春·江苏·八年级专题练习)如图,在四边形中,,,、、分别是、、的中点,若,,则等于( )
A.76° B.56° C.38° D.28°
4.(2022春·江苏徐州·八年级统考期中)若四边形的对角线互相垂直,那么顺次连结该四边形中点所得的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.以上都不对
5.(2022秋·江苏无锡·八年级无锡市天一实验学校校考阶段练习)如图,在中,,,M是AC的中点,D、E分别在AB、BC上,且,则四边形的面积为( )
A.2 B.3.2 C.3.6 D.4
6.(2022春·江苏镇江·八年级统考期中)如图,在矩形中,,,点为对角线和的交点,延长至,使,以为边向右侧作矩形,点在上,若,过点的一条直线平分该组合图形的面积,并分别交、于点、,则的值为( )
A.39 B.40 C.41 D.42
7.(2022春·江苏徐州·八年级校考阶段练习)如图,在四边形ABCD中,AB=2,CD=3,E、F分别是AD、BC中点,则EF的取值范围( )
A.0<EF<1 B.2<EF<3 C.0.5<EF<2.5 D.1<EF<5
8.(2022春·江苏南通·八年级校考期中)如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
A.2 B.4 C. D.2
二、填空题
9.(2021春·江苏宿迁·八年级校考期中)如图,为测量池塘边A、B两点的距离,小明在池塘的侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=15米,则A、B间的距离是_____米.
10.(2022春·江苏苏州·八年级校考期中)顺次连接矩形各边中点所得四边形为_____形.
11.(2022春·江苏盐城·八年级校考期中)如图,在平面直角坐标系中,的边AO,AB的中点C,D的横坐标分别是1,5,则点B的横坐标是______.
12.(2022春·江苏徐州·八年级校考阶段练习)如图,矩形ABCD的对角线AC,BD相交于点O,CEBD,DEAC.若BC=6,AB=8,则四边形CODE的周长是 _____.
13.(2022春·江苏扬州·八年级校考阶段练习)如图,在正方形中,是对角线上的点,,,,分别为垂足,连结设,分别是,的中点,,则的长为______.
14.(2021春·江苏苏州·八年级苏州工业园区星湾学校校考期中)如图,连接四边形各边中点,得到四边形,只要添加________条件,就能保证四边形是菱形.
15.(2021春·江苏扬州·八年级统考阶段练习)如图,在中,,,以为斜边作.使,,、分别是、的中点,连接、、,则的长为___________.
16.(2022秋·江苏连云港·八年级统考期中)如图,在中,,,.分别是的中点,连接;分别是的中点,连接;……按此规律进行下去,则中最短边的长度为_______.
三、解答题
17.(2019春·江苏扬州·八年级阶段练习)已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC,(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
18.(2021春·江苏南通·八年级校考阶段练习)如图,在中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当满足什么条件时,四边形图ADCF是菱形?为什么?
19.(2021春·江苏宿迁·八年级校考期中)如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?并说明理由.
20.(2020秋·江苏苏州·八年级校联考阶段练习)如图,△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.
(1)求证:MD=ME;
(2)若D为AB的中点,且AB=10,求ME的长.
21.(2022春·江苏盐城·八年级校考期中)在菱形中,两条对角线相交于点,是边的中点,连接并延长到,使,连接,.
(1)求证:四边形是矩形;
(2)求证:.
22.(2022春·江苏泰州·八年级校考阶段练习)如图,在□ABCD中,点E是AB边的中点,
(1)仅用一把无刻度的直尺画出CD边的中点F;
(2)在(1)的条件下,求证:EF=BC.
23.(2022春·江苏无锡·八年级校考阶段练习)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别是AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2.
①求∠BMN的度数;
②求BN的长.
24.(2022春·江苏泰州·八年级统考期末)如图1,D、E、F分别是各边上的点,四边形ADEF是平行四边形,有三个选项:①D是AB的中点,②E是BC的中点,③F是AC的中点.
(1)请从三个选项中选择两个作为条件,余下一个作为结论,并证明.
你选择的条件是______,结论是______(填序号);
(2)在(1)的条件下,如图2,点H在BC上,,连接DH、FH,
①若,求的度数;
②若,,连接DF,的面积为S,直接写出S的取值范围.
答案与解析
一、单选题
1.(2022春·江苏南通·八年级统考期末)如图,DE是的中位线,若DE=3,则BC的长为( )
A.4 B.5 C.6 D.8
【答案】C
【分析】根据三角形中位线的性质即可求解.
【详解】解:∵DE是的中位线,DE=3,
∴BC=6.
故选:C.
【点睛】本题考查了三角形中位线的性质,掌握中位线的性质是解题的关键.
2.(2022春·江苏·八年级专题练习)如图,平行四边形中,对角线,交于点O,点E是的中点.若,则的长为( )
A. B. C. D.
【答案】D
【分析】根据平行四边形的性质,可得出点O平分AC,则OE是三角形ABC的中位线,则AB=2OE,继而求出答案.
【详解】解:∵四边形ABCD为平行四边形,
∴AO=CO,
∵点E是CB的中点,
∴OE为△ABC的中位线,
∴AB=2OE,
∵OE=6cm ,
∴AB=12cm.
故选:D.
【点睛】本题考查了平行四边形的性质和三角形的中位线定理,关键是根据平行四边形的性质得出OE为△ABC的中位线.
3.(2022春·江苏·八年级专题练习)如图,在四边形中,,,、、分别是、、的中点,若,,则等于( )
A.76° B.56° C.38° D.28°
【答案】D
【分析】利用、分别是和两个三角形的中位线,求出,从而得出和,再根据,利用三角形内角和定理即可求出的度数.
【详解】解:∵、、分别是、、的中点,
∴、分别是和两个三角形的中位线,
∴,,且,
∴,,
∴,
又∵,
∴.
故本题答案为:D.
【点睛】本题考查了三角形内角和定理,等腰三角形的判定与性质,三角形中位线定理.解决本题的关键是正确理解题意,熟练掌握三角形中位线定理,通过等腰三角形的性质找到相等的角.
4.(2022春·江苏徐州·八年级统考期中)若四边形的对角线互相垂直,那么顺次连结该四边形中点所得的四边形一定是( )
A.矩形 B.菱形 C.正方形 D.以上都不对
【答案】A
【分析】根据三角形的中位线定理首先可以证明:顺次连接四边形各边中点所得四边形是平行四边形.再根据对角线互相垂直,即可证明平行四边形的一个角是直角,则有一个角是直角的平行四边形是矩形.
【详解】解:如图,E、F、G、H分别是AB、BC、CD、AD的中点,
∴EHFGBD,EH=FGBD;EFHGAC,EF=HGAC,
∴四边形EFGH是平行四边形,
又∵AC⊥BD,
∴EH⊥EF,∠HEF=90°
∴四边形EFGH是矩形.
故选:A.
【点睛】此题主要考查了三角形中位线定理、平行四边形的判定、矩形的判定等知识,熟练掌握三角形的中位线定理是解题的关键.
5.(2022秋·江苏无锡·八年级无锡市天一实验学校校考阶段练习)如图,在中,,,M是AC的中点,D、E分别在AB、BC上,且,则四边形的面积为( )
A.2 B.3.2 C.3.6 D.4
【答案】D
【分析】连接BM, 根据三线合一可得,进而证明,,证明,根据即可求解.
【详解】解:如图,连接BM,
∵在中,,,M是AC的中点,
∴,
∵在中,,,,
∴,,
∴,
∴(ASA),
,
∴ ,
∴.
故选D.
【点睛】本题考查了等腰三角形的性质,全等三角形的性质与判定,证明是解题的关键.
6.(2022春·江苏镇江·八年级统考期中)如图,在矩形中,,,点为对角线和的交点,延长至,使,以为边向右侧作矩形,点在上,若,过点的一条直线平分该组合图形的面积,并分别交、于点、,则的值为( )
A.39 B.40 C.41 D.42
【答案】B
【分析】根据题意可得PQ必过矩形EFGA的对角线交点,连接AF,EG交于点H,取AE的中点M,AB的中点N,连接HM,ON,过点H作HT⊥ON于T,设PQ与AD的交点为S,根据三角形中位线定理可得,∠ANO=∠ABC=90°,,∠AMH=90°,再由勾股定理可得OH的长,再证明△ASO≌△CQO,可得SO=OQ,即可求解.
【详解】解:∵过点O的一条直线平分该组合图形的面积,
∴PQ必过矩形EFGA的对角线交点,
连接AF,EG交于点H,取AE的中点M,AB的中点N,连接HM,ON,过点H作HT⊥ON于T,设PQ与AD的交点为S,
∵四边形ABCD是矩形,
∴AO=CO,
又∵点N是AB的中点,
∴,ON∥BC,
∴∠ANO=∠ABC=90°,
同理:,∠AMH=90°,
∵HT⊥NO,
∴四边形MHTN为矩形,
∴MH=NT=2,MT=MN=3,
∴TO=1,
∴,
∵AD∥BC,
∴∠DAC=∠BCA,∠ASO=∠CQO,
在△ASO和△CQO中,
∵,
∴△ASO≌△CQO(AAS),
∴SO=OQ,
同理PH=SH,
∴,
∴.
故选:B
【点睛】本题考查了矩形的性质,三角形中位线定理,全等三角形的判定和性质,勾股定理,灵活运用这些性质解决问题是本题的关键.
7.(2022春·江苏徐州·八年级校考阶段练习)如图,在四边形ABCD中,AB=2,CD=3,E、F分别是AD、BC中点,则EF的取值范围( )
A.0<EF<1 B.2<EF<3 C.0.5<EF<2.5 D.1<EF<5
【答案】C
【分析】根据三角形中位线定理求出EH、FH,根据三角形的三边关系计算即可.
【详解】解:连接AC,取AC的中点H,连接EH、FH,
∵AH=HC,AE=ED,
∴EH=CD=1.5,
同理,FH=AB=1,
在Rt△EHF中,EH﹣FH<EF<EH+FH,即0.5<EF<2.5,
故选:C.
【点睛】本题考查的是三角形中位线定理、三角形的三边关系,根据三角形中位线定理求出EH、FH是解题的关键.
8.(2022春·江苏南通·八年级校考期中)如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
A.2 B.4 C. D.2
【答案】C
【分析】根据中位线定理可得出点P的运动轨迹是线段,再根据垂线段最短可得当BP⊥时,PB取得最小值,由矩形的性质以及已知的数据即可知BP1⊥,故BP的最小值为BP1的长,由勾股定理求解即可.
【详解】如图,
当点F与点C重合时,点P在P1处,CP1=DP1,
当点F与点E重合时,点P在P2处,EP2=DP2,
∴∥CE且=,
当点F在EC上除点C、E的位置处时有DP=FP,
由中位线定理可知:P1P∥CE且P1P= ,
∴当点P的运动轨迹是线段,
∴当BP⊥时,PB取得最小值,
∵矩形ABCD中,AB=2,AD=1,E为AB的中点,
∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=1,
∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°,
∴∠DP2P1=90°,
∴∠DP1P2=45°,
∴∠P2P1B=90°,即BP1⊥,
∴BP的最小值为BP1的长,
在等腰直角三角形BCP1中,CP1=BC=1,
∴BP1=,
∴PB的最小值是,
故选:C.
【点睛】本题考查轨迹问题、矩形的性质等知识,解题的关键是学会利用特殊位置解决问题.
二、填空题
9.(2021春·江苏宿迁·八年级校考期中)如图,为测量池塘边A、B两点的距离,小明在池塘的侧选取一点O,测得OA、OB的中点分别是点D、E,且DE=15米,则A、B间的距离是_____米.
【答案】30
【分析】根据D、E是OA、OB的中点,即DE是△OAB的中位线,根据三角形的中位线定理:三角形的中位线平行于第三边且等于第三边的一半,即可求解.
【详解】解:∵D、E是OA、OB的中点,即DE是△OAB的中位线,
∴DE=AB,
∴AB=2DE=2×15=30米.
故答案为:30.
【点睛】本题考查了三角形的中位线定理应用,正确理解定理是解题的关键.
10.(2022春·江苏苏州·八年级校考期中)顺次连接矩形各边中点所得四边形为_____形.
【答案】菱
【分析】根据三角形的中位线定理和菱形的判定,顺次连接矩形各边中点所得的四边形是菱形
【详解】解:如图,连接AC、BD,
∵E、F、G、H分别是矩形ABCD的AB、BC、CD、AD边上的中点,
∴EF=GH=AC,FG=EH=BD,
∵矩形ABCD的对角线AC=BD,
∴EF=GH=FG=EH,
∴四边形EFGH是菱形.
故答案为:菱.
【点睛】此题主要考查了三角形的中位线定理,矩形的性质和菱形的判定,综合利用了三角形的中位线定理和矩形的性质是解题关键.
11.(2022春·江苏盐城·八年级校考期中)如图,在平面直角坐标系中,的边AO,AB的中点C,D的横坐标分别是1,5,则点B的横坐标是______.
【答案】8
【分析】由C、D的横坐标求出线段CD的长度,结合中位线的定义和性质,得出OB的长度,从而得到B点的横坐标.
【详解】解:∵边AO,AB的中点为点C、D,
∴CD是△OAB的中位线,CDOB,
∵点C,D的横坐标分别是1,5,
∴CD=4,
∴OB=2CD=8,
∴点B的横坐标为8.
故答案为:8.
【点睛】本题主要考查了中位线定义和性质应用,解题的关键是由点C、D的横坐标求出线段CD的长度.
12.(2022春·江苏徐州·八年级校考阶段练习)如图,矩形ABCD的对角线AC,BD相交于点O,CEBD,DEAC.若BC=6,AB=8,则四边形CODE的周长是 _____.
【答案】20
【分析】由CEBD,DEAC,可证得四边形CODE是平行四边形,又由四边形ABCD是矩形,根据矩形的性质,易得OC=OD=5,即可判定四边形CODE是菱形,继而求得答案.
【详解】解:∵CEBD,DEAC,
∴四边形CODE是平行四边形.
∵四边形ABCD是矩形,
∴AD=BC=6,OA=OC=OB=OD,∠BAD=90°,
∴,
∴OD=OC=AC=BD=5,
∴四边形CODE是菱形,
∴四边形CODE的周长为=4OC=4×5=20.
故答案为:20.
【点睛】本题考查了菱形的判定与性质以及矩形的性质,勾股定理.此题难度不大,注意证得四边形CODE是菱形是解答此题的关键.
13.(2022春·江苏扬州·八年级校考阶段练习)如图,在正方形中,是对角线上的点,,,,分别为垂足,连结设,分别是,的中点,,则的长为______.
【答案】2.5
【分析】如图所示。连接AG,CG,先证明△ABG≌△CBG(SSS),得到AG=CG,再证四边形ECFG是矩形,得到CG=EF=5,最后证明MN是△ABG的中位线,则.
【详解】解:如图所示。连接AG,CG,
∵四边形ABCD是正方形,
∴BA=BC,∠ABG=∠CBG,∠BCD=90°,
又∵BG=BG,
∴△ABG≌△CBG(SSS),
∴AG=CG,
∵GF⊥BC,GE⊥CD,∠ECF=90°,
∴四边形ECFG是矩形,
∴CG=EF=5,
∵M、N分别是AB,BG的中点,
∴MN是△ABG的中位线,
∴,
故答案为:2.5.
【点睛】本题主要考查了正方形的性质,全等三角形的性质与判定,矩形的性质与判定,三角形中位线定理,正确作出辅助线构造全等三角形是解题的关键.
14.(2021春·江苏苏州·八年级苏州工业园区星湾学校校考期中)如图,连接四边形各边中点,得到四边形,只要添加________条件,就能保证四边形是菱形.
【答案】
【分析】先证明中点四边形为平行四边形,则只需让一组邻边相等即可,而邻边都等于对角线的一半,那么添加对角线需相等即可.
【详解】解:添加时,四边形为菱形.
∵点E、F、G、H分别为、、、的中点,
∴,,,,,,
∴,,
∴四边形为平行四边形,
当时,,
∴四边形为菱形.
故答案为:.
【点睛】本题考查菱形的判定,三角形的中位线定理,解题的关键是熟悉菱形的判定定理,难度不大.
15.(2021春·江苏扬州·八年级统考阶段练习)如图,在中,,,以为斜边作.使,,、分别是、的中点,连接、、,则的长为___________.
【答案】
【分析】根据直角三角形的性质得到,根据三角形的外角性质得到,根据三角形中位线定理得到,,推出,利用勾股定理即可求解.
【详解】解:∵,F是的中点,
∴,
∴,
∴,
∵E、F分别是、的中点,
∴,,
∴,
∴,
∴.
故答案为:.
【点睛】本题考查的是直角三角形的性质、等腰三角形的性质、三角形外角的性质、三角形中位线定理,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.
16.(2022秋·江苏连云港·八年级统考期中)如图,在中,,,.分别是的中点,连接;分别是的中点,连接;……按此规律进行下去,则中最短边的长度为_______.
【答案】##
【分析】根据已知条件和图形的变化可得前几个图形中最短边的长度,找出规律,可得结论.
【详解】解:在中,,,,是的中点,
∴,
中最短边的边长为,
中最短边的边长为,
中最短边的边长为,
∴中最短边的边长为,
则中最短边的边长为,,
故答案为:.
【点睛】本题主要考查了规律型,图形的变化类,解决本题的关键是观察图形变化寻找规律.
三、解答题
17.(2019春·江苏扬州·八年级阶段练习)已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC,(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
【答案】(1)见解析;(2)4cm.
【分析】(1)根据三角形中位线定理可得ED∥FC;结合已知条件EF∥DC,即可得结论;
(2)根据直角三角形中,斜边上的中线等于斜边的一半得到AB=2DC.
【详解】(1)证明:如图,∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)解:由(1)知,四边形CDEF是平行四边形,则DC=EF=2cm.
∵点D是Rt△ABC斜边AB的中点,
∴DC= AB,
∴AB=2DC=4cm.
故答案为(1)见解析;(2)4cm.
【点睛】本题考查平行四边形的判定与性质,直角三角形斜边上的中线.解题的关键是熟练掌握平行四边形的判定与性质以及直角三角形斜边上的中线等于斜边的一半.
18.(2021春·江苏南通·八年级校考阶段练习)如图,在中,点D、E分别是边BC、AC的中点,过点A作交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当满足什么条件时,四边形图ADCF是菱形?为什么?
【答案】(1)见解析;(2)当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,理由见解析.
【分析】(1)首先利用平行四边形的判定方法得出四边形ABDF是平行四边形,进而得出AF=DC,利用一组对边相等且平行的四边形是平行四边形,进而得出答案;
(2)利用直角三角形的性质结合菱形的判定方法得出即可.
【详解】(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,BD=CD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)解:当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,
理由:∵△ABC是直角三角形,且∠BAC=90°
又∵点D是边BC的中点,
∴AD=DC,
∴平行四边形ADCF是菱形.
【点睛】本题考查平行四边形的判定与性质以及菱形的判定,熟练应用平行四边形的判定与性质是解题关键.
19.(2021春·江苏宿迁·八年级校考期中)如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC内的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
(1)求证:四边形DGFE是平行四边形;
(2)若四边形DGFE是菱形,则OA与BC应满足怎样的数量关系?并说明理由.
【答案】(1)证明见解析
(2)OA=BC,理由见解析
【分析】(1)首先利用三角形中位线的性质得出DEBC,DE=BC,GFBC,GF=BC,从而得出DEGF,DE=GF,即可证得四边形DGFE是平行四边形;
(2)由四边形DGFE是菱形,可得DG=GF,再根据三角形中位线的性质可得DG=OA,GF=BC,从而得出OA=BC.
(1)
证明:∵D、E分别是边AB、AC的中点.
∴DEBC,DE=BC.
∵点G、F分别是OB、OC的中点,
∴GFBC,GF=BC.
∴DEGF,DE=GF.
∴四边形DEFG是平行四边形;
(2)
解:OA=BC,理由如下:
连接OA.
∵四边形DEFG是菱形,
∴DG=GF,
∵D是AB的中点,点G、F分别是OB、OC的中点,
∴DG=OA,GF=BC,
∴OA=BC.
【点睛】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,菱形的判定以及平行四边形与菱形的关系,熟记相关的定理和性质是解题的关键.
20.(2020秋·江苏苏州·八年级校联考阶段练习)如图,△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE.
(1)求证:MD=ME;
(2)若D为AB的中点,且AB=10,求ME的长.
【答案】(1)见解析
(2)ME=5
【分析】(1)根据等腰三角形的性质求出∠B=∠C,求出BM=CM,根据全等三角形的判定得出△DBM≌△ECM,根据全等三角形的性质得出即可;
(2)根据三角形的中位线求出DM=AC,代入求出即可.
(1)
证明:∵AB=AC,
∴∠B=∠C,
∵M是BC的中点,
∴BM=CM,
在△DBM和△ECM中,
,
∴△DBM≌△ECM(SAS),
∴MD=ME;
(2)
解:∵M是BC的中点,D为AB的中点,
∴DM=AC,
∵AB=10,
∴AC=AB=10,
∴ME=DM=5.
【点睛】本题考查了全等三角形的性质和判定,三角形中位线的应用,能求出△DBM≌△ECM和DM=AC是解此题的关键.
21.(2022春·江苏盐城·八年级校考期中)在菱形中,两条对角线相交于点,是边的中点,连接并延长到,使,连接,.
(1)求证:四边形是矩形;
(2)求证:.
【答案】(1)见解析
(2)见解析
【分析】(1)由菱形ABCD可得出,由F是CD的中点、EF=OF,证四边形OCED是平行四边形,进而得出结论;
(2)证明是的中位线即可得出结论.
(1)
证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴,
∵是边的中点,
∴CF=DF,
又,
∴四边形OCED是平行四边形,
∵,
∴四边形OCED是矩形;
(2)
∵四边形是矩形,
∴,
∵四边形是菱形,
∴,
∴是的中位线,
∴.
【点睛】本题考查了菱形的性质,平行四边形的性质和判定,矩形的判定和性质,三角形中位线的性质,掌握以上知识是解题的关键.
22.(2022春·江苏泰州·八年级校考阶段练习)如图,在□ABCD中,点E是AB边的中点,
(1)仅用一把无刻度的直尺画出CD边的中点F;
(2)在(1)的条件下,求证:EF=BC.
【答案】(1)见详解
(2)见详解
【分析】(1)连接AC、BD,两者交于点G,连接EG并延长交CD与点F,即可.
(2)证明四边形ADFE是平行四边形即可.
(1)
作图如下:
点F即为所求,
证明:∵四边形ABCD是平行四边形,
∴,,CD=AB,对角线交点G平分对角线AC、BD,
∴点G为AC、BD的中点,
∵E点为AB中点,
∴EG为△ABD的中位线,
∴,即,
∵,
∴四边形ADFE是平行四边形,
∴AE=DF,
∵E点为AB中点,
∴,
∴,即有,
∴F点为DC中点,
即F点满足要求.
(2)
证明:在(1)中已证明有:四边形ADFE是平行四边形,
∴AD=EF,
∵AD=BC,
∴EF=BC,
结论得证.
【点睛】本题主要考查了基本作图,平行四边形的判定与性质、中位线的判定与性质等知识,掌握平行四边形的性质是解答本题的关键.注意作图只能用无刻度直尺,并非尺规作图.
23.(2022春·江苏无锡·八年级校考阶段练习)如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别是AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2.
①求∠BMN的度数;
②求BN的长.
【答案】(1)答案见解析
(2)①∠BMN=90°;②BN=
【分析】(1)在△CAD中,由中位线定理得到MNAD,且MN=AD,在Rt△ABC中,因为M是AC的中点,故BM=AC,即可得到结论;
(2)①由∠BAD=60°且AC平分∠BAD,得到∠BAC=∠DAC=30°,由(1)知,BM=AC=AM=MC,得到∠BMC =60°,由平行线性质得到∠NMC=∠DAC=30°,故∠BMN=90°;②因为∠BMN=90°,由勾股定理得到,BN2=BM2+MN2,再由MN=BM=1,得到BN的长.
(1)
解:在△CAD中,∵M、N分别是AC、CD的中点,
∴MNAD,且MN=AD,
在Rt△ABC中,∵M是AC的中点,
∴BM=AC,
又∵AC=AD,
∴MN=BM;
(2)
①∵∠BAD=60°且AC平分∠BAD,
∴∠BAC=∠DAC=30°,
由(1)知,BM=AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MNAD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°;
②∵∠BMN=90°,
∴BN2=BM2+MN2,
而由(1)知,MN=BM=AC=×2=1,
∴BN=.
【点睛】本题考查了三角形中位线定理、直角三角形斜边中线定理、三角形的外角、勾股定理等知识,解题的关键是灵活应用三角形的中位线平行于第三边,并且等于第三边的一半.
24.(2022春·江苏泰州·八年级统考期末)如图1,D、E、F分别是各边上的点,四边形ADEF是平行四边形,有三个选项:①D是AB的中点,②E是BC的中点,③F是AC的中点.
(1)请从三个选项中选择两个作为条件,余下一个作为结论,并证明.
你选择的条件是______,结论是______(填序号);
(2)在(1)的条件下,如图2,点H在BC上,,连接DH、FH,
①若,求的度数;
②若,,连接DF,的面积为S,直接写出S的取值范围.
【答案】(1)①②;③
(2)①80°;②
【分析】(1)无论选哪两个作为条件,利用平行四边形的性质及三角形中位线性质定理,均可证明余下的那一个作为结论成立;
(2)①由直角三角形斜边上中线的性质、等腰三角形的性质即可求得结果;
②连接DF,由三角形中位线定理得DF∥BC,则,从而有,再由三角形的中线平分三角形面积知,由平行四边形可得,过点B作BM⊥AC于M,由垂线段最短可求得△ABC面积的最大值,从而可求得S的范围.
(1)
(1)选择条件①②,结论为③,证明如下:
∵D是AB的中点,E是BC的中点,
∴DE是△ABC的中位线,
∴,
∵四边形ADEF是平行四边形,
∴DE=AF,
∴,
∴F是AC的中点;
故答案为:①②,③;
同理可证:当①③为条件,②为结论;或②③为条件,①为结论;
(2)
①∵AH⊥BC,D为AB的中点,
∴DH为Rt△ABH斜边上的中线,
∴,
∴∠DAH=∠DHA;
同理:∠FAH=∠FHA,
∴∠DHF =∠DHA+∠FHA=∠DAH+∠FAH=∠BAC=180° (∠B+∠C)=80°;
②连接DF,如图,
∵D、F分别是AB、AC的中点,
∴DF是△ABC的中位线
∴DF//BC,
∴,
∴,
∵DH、FH分别是Rt△ABH、Rt△ACH斜边上的中线,
∴,,
∴,
∵四边形ADEF是平行四边形,
∴,
∴
∴
∴;
过点B作BM⊥AC于M,
则BM≤AB=8,
∴
即△ABC面积的最大值为40,
∴,
∵S>0,
∴S的范围为.
【点睛】本题考查了三角形中位线定理,直角三角形斜边上中线的性质,三角形中线平分三角形的面积的性质,平行四边形的性质,等腰三角形的性质,垂线段最短等知识,具有一定的综合性.灵活运用这些知识是解题的关键.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
