3.1 圆 课件（共21张PPT）

(共21张PPT)
第三章 圆
北师大版九年级数学下册
1.圆
学习&目标
1.认识圆，理解圆的本质属性.（重点）
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念，并了解它们之间的区别和联系.（难点）
3.初步了解点与圆的位置关系.
情境&导入
为什么车轮要做成圆形？
情境&导入
圆是常见的图形，生活中的许多物体都给我们以圆的形象（如图）.
探索&交流
一些学生正在做投圈游戏，他们呈“一”字排开．这样的队形对每一人都公平吗？你认为他们应当排成什么样的队形？
因为每个人到目标物的距离不相等，所以不公平。
通过这节课的学习，我们就知道怎么排队形了。
·
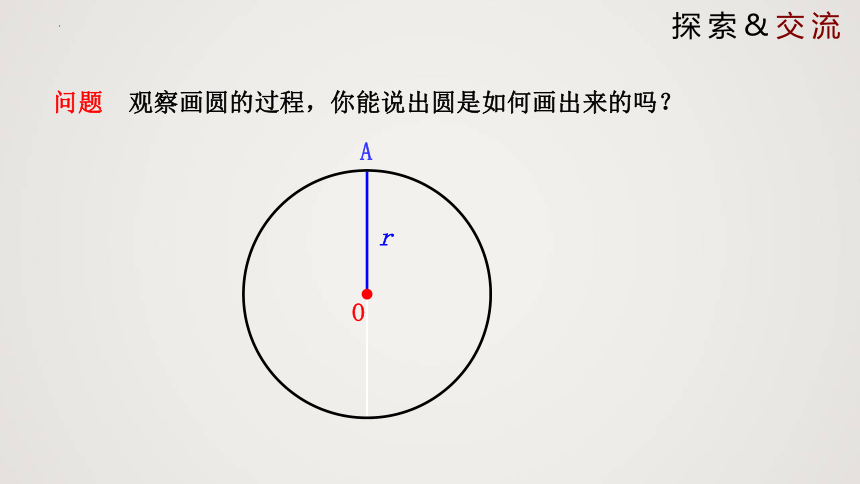
r
O
A
问题 观察画圆的过程，你能说出圆是如何画出来的吗？
探索&交流
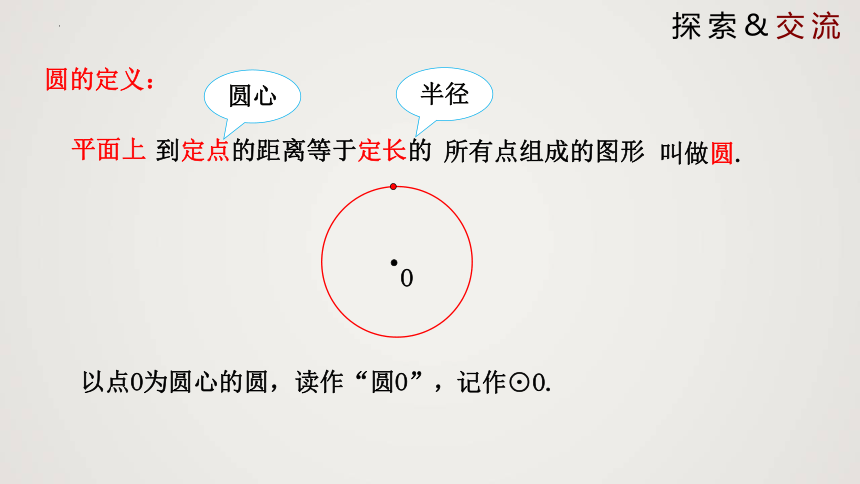
圆的定义：
所有点组成的图形
平面上
叫做圆.
到定点的距离等于定长的
O
圆心
半径
以点O为圆心的圆，读作“圆O”，
记作⊙O.
探索&交流
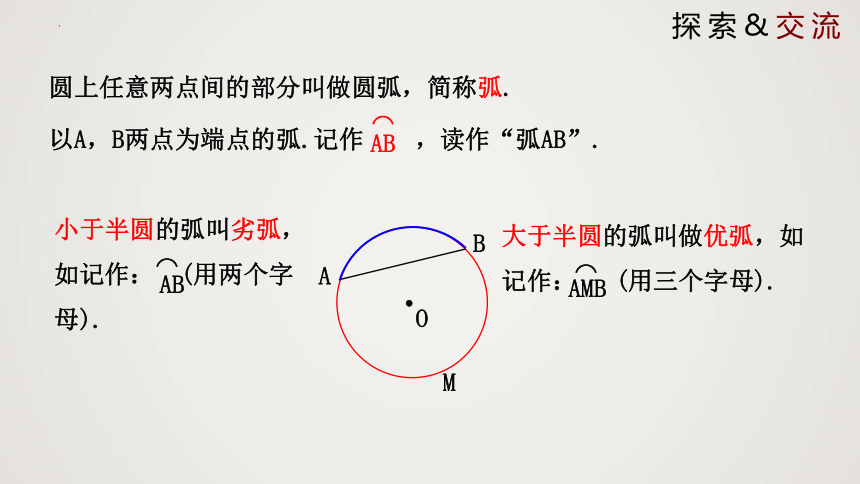
以A，B两点为端点的弧.记作 ，读作“弧AB”.
AB
⌒
O
A
B
圆上任意两点间的部分叫做圆弧，简称弧.
小于半圆的弧叫劣弧，如记作： (用两个字母).
AB
⌒
大于半圆的弧叫做优弧，如记作： (用三个字母).
⌒
AMB
M
探索&交流
特别提醒
1.确定一个圆需要“两个要素”，一是圆心：圆心定其位置，二是半径：半径定其大小.
2.圆是一条封闭的曲线，曲线是“圆周”,而不能认为是“圆面”.
3.“圆上的点”指圆周上的点.
探索&交流
例题&解析
例题欣赏

例1.下列说法中, 错误的有( )
(1)经过点P 的圆有无数个；
(2)以点P 为圆心的圆有无数个；
(3)半径为3 cm 且经过点P 的圆有无数个；
(4)以点P 为圆心，3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
A
O
B
连接圆上任意两点间的线段叫做弦.（如弦AB）
经过圆心的弦叫做直径.（如直径CD）
D
C
A
探索&交流
圆的任意一条直径将圆分成两条弧，每一条弧都叫半圆.
O
B
D
C
A
能够重合的两个圆叫做等圆.
在同圆或等圆中，能够互相重合的弧叫做等弧.
半径相等的两个圆是等圆；
反过来，同圆或等圆的半径相等.
注意：等弧不是指弧长相等.
探索&交流
劣弧与优弧
·
C
O
A
B
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
探索&交流
例题&解析
例题欣赏

例2.下列语句中正确的有（ ）
①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；
④长度相等的两条弧是等弧；⑤半圆是弧，弧不一定是半圆.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
C
探索&交流
　想一想
如图，⊙O是一个半径为r的圆 ，在圆内、圆上、圆外分别取一点，点到圆心的距离为d，你能用r与d的大小关系刻画它们的位置特征吗？
O
r
A
点在圆内
d＜r
B
点在圆上
d＝r
C
点在圆外
d＞r
探索&交流
要点归纳
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r＜d＜R
数形结合：
位置关系
数量关系
例题&解析
例题欣赏

x
x
x
x
例3.如图，在扇形MON中， ，半径MO=NO=10，正方形ABCD的顶点B、C、D在半径上，顶点A在圆弧上，求正方形ABCD的边长.
解：连接OA.
∵ABCD为正方形
∴DC=CO
设OC=x,则AB=BC=DC=OC=x
又∵OA=OM=10
∴在Rt△ABO中,
∴AB=BC=CD,∠ABC=∠DCB=90°
又∵∠DOC=45°
练习&巩固
1.下列条件中，能确定唯一一个圆的是( )
A. 以点O 为圆心
B. 以2 cm 长为半径
C. 以点O 为圆心，5 cm长为半径
D. 半径为2 cm 且经过点A
练习&巩固
2.平面内已知点P，以P为圆心，3 cm为半径作圆，这样的圆可以作(　　)
A．1个 B．2个 C．3个 D．无数个
练习&巩固
1
·
2cm
3cm
3.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
小结&反思
O
r
A
点在圆内
d＜r
B
点在圆上
d＝r
C
点在圆外
d＞r
所有点组成的图形
平面上
叫做圆.
到定点的距离等于定长的