3.3 垂径定理 课件(共22张PPT)
文档属性
| 名称 | 3.3 垂径定理 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 975.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 17:37:23 | ||
图片预览







文档简介
(共22张PPT)
第三章 圆
北师大版九年级数学下册
3 垂径定理
学习&目标
1.进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.(重点)
3.灵活运用垂径定理解决有关圆的问题.(难点)
情境&导入
1.等腰三角形是轴对称图形吗?
2.如果将一等腰三角形沿底边上的高对折,可以发现什么结论?
3.如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画圆,得到的图形是否是轴对称图形呢?
情境&导入
问题:你知道赵州桥吗 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
37.4m
7.2m
探索&交流
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你的理由.
C
D
A
B
M
O
C
D
A
B
M
O
连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时, 点A与点B重合,
探索&交流
(2)① CD是直径
② CD⊥AB
可推得
条件
③AM=BM,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
结论
解:(1)此图是轴对称图形,对称轴是直径CD所在的直线
C
D
A
B
M
O
探索&交流
C
D
A
B
M
O
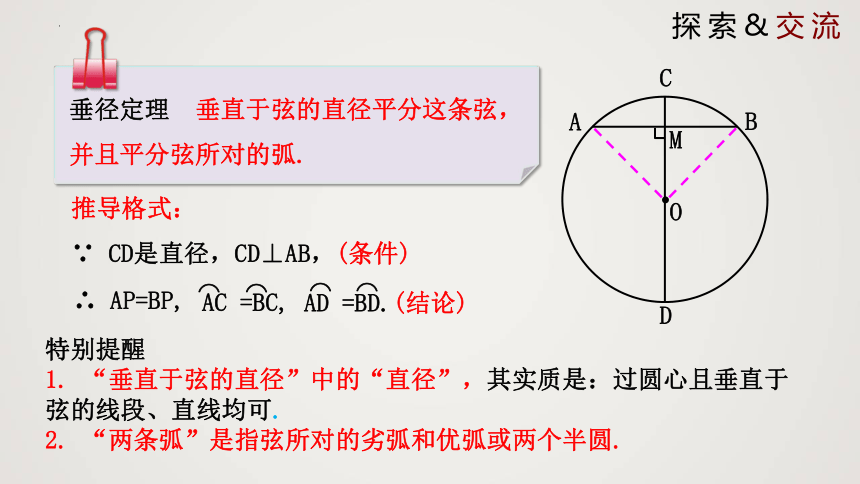
垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的弧.
特别提醒
1. “垂直于弦的直径”中的“直径”,其实质是:过圆心且垂直于弦的线段、直线均可.
2. “两条弧”是指弦所对的劣弧和优弧或两个半圆.
探索&交流
∵ CD是直径,CD⊥AB,(条件)
∴ AP=BP,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.(结论)
推导格式:
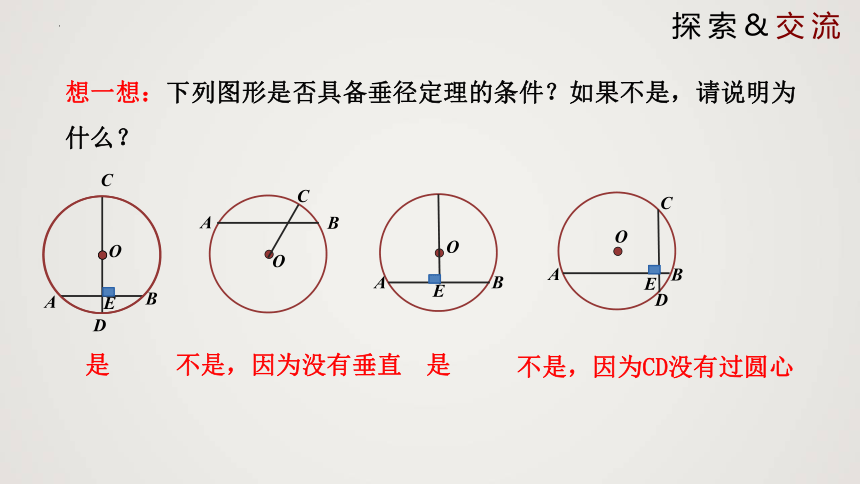
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
探索&交流
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
归纳总结
探索&交流
例题&解析
例题欣赏
例1.已知:在☉O中,CD是直径,AB是弦,AB⊥CD,垂足为M. 求证:AM=BM,AC =BC,AD =BD.
⌒
⌒
⌒
⌒
O
C
D
M
A
B
证明:连接OA、OB、CA、CB,则OA=OB.
即△AOB是等腰三角形.
∵AB⊥CD,
∴AM=BM,∠AOC=∠BOC.
⌒
⌒
AC =BC.
∴AD =BD,
⌒
⌒
从而∠AOD=∠BOD.
例题&解析
例题欣赏
例2.如图所示,弦CD 垂直于⊙ O 的直径AB,垂足为点H,
且CD=2 ,BD= ,则AB 的长为( )
A. 2 B. 3
C. 4 D. 5
B
探索&交流
想一想
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心;②垂直于弦;③平分弦;
④平分弦所对的优弧; ⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
探索&交流
D
O
A
B
E
C
举例证明其中一种组合方法
已知:
求证:
① CD是直径
② CD⊥AB,垂足为E
③ AE=BE
④ AC=BC ⑤ AD=BD
⌒
⌒
⌒
⌒
证明猜想
AC与BC相等吗? AD与BD相等吗?为什么?
如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
·
O
A
B
C
D
E
⌒
⌒
(2)由垂径定理可得AC =BC, AD =BD.
⌒
⌒
⌒
⌒
(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
⌒
⌒
探索&交流
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
归纳总结
探索&交流
例题&解析
例题欣赏
例3.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.
·
O
A
B
E
C
D
解:连接OA,∵ CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
例题&解析
例题欣赏
例4.如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.
● O
C
D
E
F
┗
解:连接OC.
设这段弯路的半径为Rm,则OF=(R-90)m.
根据勾股定理,得
解得R=545.
∴这段弯路的半径约为545m.
练习&巩固
1.下列说法中,不正确的是( )
A. 圆既是轴对称图形,又是中心对称图形
B. 圆绕着它的圆心旋转任意角度,都能与它自身重合
C. 圆的对称轴有无数条,对称中心只有一个
D. 圆的每一条直径都是它的对称轴
练习&巩固
2.一块圆形宣传标志牌如图所示,点A,B,C 在⊙ O 上,CD 垂直平分AB 于点D.现测得AB=8 dm,DC=2 dm,则圆形标志牌的半径为______.
练习&巩固
3.如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为_______.
小结&反思
在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
涉及垂径定理时辅助线的添加方法
弦a,弦心距d,弓形高h,半径r之间有以下关系:
弓形中重要数量关系
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
第三章 圆
北师大版九年级数学下册
3 垂径定理
学习&目标
1.进一步认识圆,了解圆是轴对称图形.
2.理解垂直于弦的直径的性质和推论,并能应用它解决一些简单的计算、证明和作图问题.(重点)
3.灵活运用垂径定理解决有关圆的问题.(难点)
情境&导入
1.等腰三角形是轴对称图形吗?
2.如果将一等腰三角形沿底边上的高对折,可以发现什么结论?
3.如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画圆,得到的图形是否是轴对称图形呢?
情境&导入
问题:你知道赵州桥吗 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37m, 拱高(弧的中点到弦的距离)为7.23m,你能求出赵州桥主桥拱的半径吗?
37.4m
7.2m
探索&交流
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
(2)你能发现图中有哪些等量关系?说一说你的理由.
C
D
A
B
M
O
C
D
A
B
M
O
连接OA,OB,则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时, 点A与点B重合,
探索&交流
(2)① CD是直径
② CD⊥AB
可推得
条件
③AM=BM,
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
结论
解:(1)此图是轴对称图形,对称轴是直径CD所在的直线
C
D
A
B
M
O
探索&交流
C
D
A
B
M
O
垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的弧.
特别提醒
1. “垂直于弦的直径”中的“直径”,其实质是:过圆心且垂直于弦的线段、直线均可.
2. “两条弧”是指弦所对的劣弧和优弧或两个半圆.
探索&交流
∵ CD是直径,CD⊥AB,(条件)
∴ AP=BP,
⌒
⌒
AC =BC,
⌒
⌒
AD =BD.(结论)
推导格式:
想一想:下列图形是否具备垂径定理的条件?如果不是,请说明为什么?
是
不是,因为没有垂直
是
不是,因为CD没有过圆心
A
B
O
C
D
E
O
A
B
C
A
B
O
E
A
B
D
C
O
E
探索&交流
垂径定理的几个基本图形:
A
B
O
C
D
E
A
B
O
E
D
A
B
O
D
C
A
B
O
C
归纳总结
探索&交流
例题&解析
例题欣赏
例1.已知:在☉O中,CD是直径,AB是弦,AB⊥CD,垂足为M. 求证:AM=BM,AC =BC,AD =BD.
⌒
⌒
⌒
⌒
O
C
D
M
A
B
证明:连接OA、OB、CA、CB,则OA=OB.
即△AOB是等腰三角形.
∵AB⊥CD,
∴AM=BM,∠AOC=∠BOC.
⌒
⌒
AC =BC.
∴AD =BD,
⌒
⌒
从而∠AOD=∠BOD.
例题&解析
例题欣赏
例2.如图所示,弦CD 垂直于⊙ O 的直径AB,垂足为点H,
且CD=2 ,BD= ,则AB 的长为( )
A. 2 B. 3
C. 4 D. 5
B
探索&交流
想一想
如果把垂径定理(垂直于弦的直径平分弦,并且平分弦所对的两条弧)结论与题设交换一条,命题是真命题吗?
①过圆心;②垂直于弦;③平分弦;
④平分弦所对的优弧; ⑤平分弦所对的劣弧.
上述五个条件中的任何两个条件都可以推出其他三个结论吗?
探索&交流
D
O
A
B
E
C
举例证明其中一种组合方法
已知:
求证:
① CD是直径
② CD⊥AB,垂足为E
③ AE=BE
④ AC=BC ⑤ AD=BD
⌒
⌒
⌒
⌒
证明猜想
AC与BC相等吗? AD与BD相等吗?为什么?
如图,AB是⊙O的一条弦,作直径CD,使AE=BE.
(1)CD⊥AB吗?为什么?
(2)
·
O
A
B
C
D
E
⌒
⌒
(2)由垂径定理可得AC =BC, AD =BD.
⌒
⌒
⌒
⌒
(1)连接AO,BO,则AO=BO,
又AE=BE,∴△AOE≌△BOE(SSS),
∴∠AEO=∠BEO=90°,
∴CD⊥AB.
⌒
⌒
探索&交流
思考:“不是直径”这个条件能去掉吗?如果不能,请举出反例.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
垂径定理的推论
·
O
A
B
C
D
特别说明:
圆的两条直径是互相平分的.
归纳总结
探索&交流
例题&解析
例题欣赏
例3.如图,⊙O的弦AB=8cm ,直径CE⊥AB于D,DC=2cm,求半径OC的长.
·
O
A
B
E
C
D
解:连接OA,∵ CE⊥AB于D,
∴
设OC=xcm,则OD=x-2,根据勾股定理,得
解得 x=5,
即半径OC的长为5cm.
x2=42+(x-2)2,
例题&解析
例题欣赏
例4.如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.
● O
C
D
E
F
┗
解:连接OC.
设这段弯路的半径为Rm,则OF=(R-90)m.
根据勾股定理,得
解得R=545.
∴这段弯路的半径约为545m.
练习&巩固
1.下列说法中,不正确的是( )
A. 圆既是轴对称图形,又是中心对称图形
B. 圆绕着它的圆心旋转任意角度,都能与它自身重合
C. 圆的对称轴有无数条,对称中心只有一个
D. 圆的每一条直径都是它的对称轴
练习&巩固
2.一块圆形宣传标志牌如图所示,点A,B,C 在⊙ O 上,CD 垂直平分AB 于点D.现测得AB=8 dm,DC=2 dm,则圆形标志牌的半径为______.
练习&巩固
3.如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为_______.
小结&反思
在圆中有关弦长a,半径r, 弦心距d(圆心到弦的距离),弓形高h的计算题,常常通过连半径或作弦心距构造直角三角形,利用垂径定理和勾股定理求解.
涉及垂径定理时辅助线的添加方法
弦a,弦心距d,弓形高h,半径r之间有以下关系:
弓形中重要数量关系
A
B
C
D
O
h
r
d
d+h=r
O
A
B
C
·
